Abstract
Spontaneous symmetry breaking is a fundamental concept in many areas of physics, including cosmology, particle physics and condensed matter1. An example is the breaking of spatial translational symmetry, which underlies the formation of crystals and the phase transition from liquid to solid. Using the analogy of crystals in space, the breaking of translational symmetry in time and the emergence of a ‘time crystal’ was recently proposed2,3, but was later shown to be forbidden in thermal equilibrium4,5,6. However, non-equilibrium Floquet systems, which are subject to a periodic drive, can exhibit persistent time correlations at an emergent subharmonic frequency7,8,9,10. This new phase of matter has been dubbed a ‘discrete time crystal’10. Here we present the experimental observation of a discrete time crystal, in an interacting spin chain of trapped atomic ions. We apply a periodic Hamiltonian to the system under many-body localization conditions, and observe a subharmonic temporal response that is robust to external perturbations. The observation of such a time crystal opens the door to the study of systems with long-range spatio-temporal correlations and novel phases of matter that emerge under intrinsically non-equilibrium conditions7.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Chaikin, P. & Lubensky, T. Principles of Condensed Matter Physics Vol. 1 (Cambridge Univ. Press, 1995)
Wilczek, F. Quantum time crystals. Phys. Rev. Lett. 109, 160401 (2012)
Wilczek, F. Superfluidity and space-time translation symmetry breaking. Phys. Rev. Lett. 111, 250402 (2013)
Bruno, P. Comment on “quantum time crystals”. Phys. Rev. Lett. 110, 118901 (2013)
Bruno, P. Impossibility of spontaneously rotating time crystals: a no-go theorem. Phys. Rev. Lett. 111, 070402 (2013)
Watanabe, H. & Oshikawa, M. Absence of quantum time crystals. Phys. Rev. Lett. 114, 251603 (2015)
Khemani, V., Lazarides, A., Moessner, R. & Sondhi, S. L. Phase structure of driven quantum systems. Phys. Rev. Lett. 116, 250401 (2016)
Else, D. V., Bauer, B. & Nayak, C. Floquet time crystals. Phys. Rev. Lett. 117, 090402 (2016)
von Keyserlingk, C. W., Khemani, V. & Sondhi, S. L. Absolute stability and spatiotemporal long-range order in Floquet systems. Phys. Rev. B 94, 085112 (2016)
Yao, N. Y., Potter, A. C., Potirniche, I.-D. & Vishwanath, A. Discrete time crystals: rigidity, criticality, and realizations. Phys. Rev. Lett. 118, 030401 (2017)
Sachdev, S. Quantum Phase Transitions (Cambridge Univ. Press, 1999)
Li, T. et al. Space-time crystals of trapped ions. Phys. Rev. Lett. 109, 163001 (2012)
Sacha, K. Modeling spontaneous breaking of time-translation symmetry. Phys. Rev. A 91, 033617 (2015)
Nandkishore, R. & Huse, D. A. Many-body localization and thermalization in quantum statistical mechanics. Annu. Rev. Condens. Matter Phys. 6, 15–38 (2015)
D’Alessio, L. & Rigol, M. Long-time behavior of isolated periodically driven interacting lattice systems. Phys. Rev. X 4, 041048 (2014)
Lazarides, A., Das, A. & Moessner, R. Equilibrium states of generic quantum systems subject to periodic driving. Phys. Rev. E 90, 012110 (2014)
Ponte, P., Chandran, A., Papic, Z. & Abanin, D. A. Periodically driven ergodic and many-body localized quantum systems. Ann. Phys. 353, 196–204 (2015)
Else, D. V., Bauer, B. & Nayak, C. Pre-thermal time crystals and Floquet topological phases without disorder. Preprint at http://arXiv.org/abs/1607.05277 (2016)
Smith, J. et al. Many-body localization in a quantum simulator with programmable random disorder. Nat. Phys. 12, 907–911 (2016)
Lee, A. C. et al. Engineering large Stark shifts for control of individual clock state qubits. Phys. Rev. A 94, 042308 (2016)
Porras, D. & Cirac, J. I. Effective quantum spin systems with trapped ions. Phys. Rev. Lett. 92, 207901 (2004)
Brown, K. R., Harrow, A. W. & Chuang, I. L. Arbitrarily accurate composite pulse sequences. Phys. Rev. A 70, 052318 (2004)
Burin, A. L. Localization in a random XY model with long-range interactions: intermediate case between single-particle and many-body problems. Phys. Rev. B 92, 104428 (2015)
Yao, N. Y. et al. Many-body localization in dipolar systems. Phys. Rev. Lett. 113, 243002 (2014)
Bordia, P., Luschen, H., Schneider, U., Kanp, M. & Bloch, I. Periodically driving a many-body localized quantum system. Preprint at http://arXiv.org/abs/1607.07868 (2016)
von Keyserlingk, C. W. & Sondhi, S. L. Phase structure of one-dimensional interacting Floquet systems. I. Abelian symmetry-protected topological phases. Phys. Rev. B 93, 245145 (2016)
Potter, A. C., Morimoto, T. & Vishwanath, A. Classification of interacting topological Floquet phases in one dimension. Phys. Rev. X 6, 041001 (2016)
Jotzu, G. et al. Experimental realization of the topological Haldane model with ultracold fermions. Nature 515, 237–240 (2014)
Else, D. V. & Nayak, C. Classification of topological phases in periodically driven interacting systems. Phys. Rev. B 93, 201103(R) (2016)
von Keyserlingk, C. W. & Sondhi, S. L. Phase structure of one-dimensional interacting Floquet systems. II. Symmetry-broken phases. Phys. Rev. B 93, 245146 (2016)
Olmschenk, S. et al. Manipulation and detection of a trapped Yb+ hyperfine qubit. Phys. Rev. A 76, 052314 (2007)
Hayes, D. et al. Entanglement of atomic qubits using an optical frequency comb. Phys. Rev. Lett. 104, 140501 (2010)
Kim, K. et al. Entanglement and tunable spin-spin couplings between trapped ions using multiple transverse modes. Phys. Rev. Lett. 103, 120502 (2009)
Acknowledgements
We acknowledge discussions with M. Zaletel and D. Stamper-Kurn. This work was supported by the ARO Atomic and Molecular Physics Program, the AFOSR MURI on Quantum Measurement and Verification, the IARPA LogiQ program, the IC Postdoctoral Research Fellowship Program, the NSF Physics Frontier Center at JQI (and the PFC Seed Grant), and the Miller Institute for Basic Research in Science. A.V. was supported by the AFOSR MURI grant FA9550- 14-1-0035 and the Simons Investigator Program. N.Y.Y. acknowledges support from the LDRD Program of LBNL under US DOE Contract No. DE-AC02-05CH11231.
Author information
Authors and Affiliations
Contributions
J.Z., P.W.H., A.K., P.B., A.L., J.S., G.P. and C.M. all contributed to experimental design, construction, data collection and analysis. I.-D.P., A.C.P., A.V. and N.Y.Y. all contributed to the theory for the experiment. All work was performed under the guidance of N.Y.Y. and C.M. All authors contributed to this manuscript.
Corresponding author
Ethics declarations
Competing interests
C.M. is a founding scientist of ionQ, Inc.
Additional information
Reviewer Information Nature thanks H. Haeffner and the other anonymous reviewer(s) for their contribution to the peer review of this work.
Extended data figures and tables
Extended Data Figure 1 Experimental pulse sequence.
Bottom left, we initialize the spins via optical pumping plus a spin rotation, and then start the Floquet evolution. Each period includes the three parts of the Hamiltonian as described in the main text and Methods (top left), and is repeated for 100 times. We then perform an analysis rotation to the desired direction on the Bloch sphere, and then perform spin state detection (bottom right). Inset at top right, all pulses in the Floquet evolution are shaped with a ‘Tukey’ window. See text for detailed explanations.
Extended Data Figure 2 Build-up of a DTC.
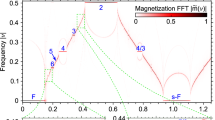
From a to b to c, we fix the disorder instance (that is, a single sample of the random disorder realizations) and the perturbation ε, while gradually increasing the interactions (2J0t2) for different experimental runs. The temporal oscillations are synchronized with increasing interactions, and the Fourier subharmonic peak is enhanced. The top panel shows the time-traces of the individual spin magnetizations, and the bottom panel shows the Fourier spectrum.
Extended Data Figure 3 Comparing the ions’ dynamics with and without disorder.
a, Without disorder (W0t3 set to 0), the spin–spin interactions suppress the beatnote imposed by the external perturbation ε. Left, experimental data; right, exact numerics calculated under Floquet time-evolution. b, With disorder (W0t3 = π), the time crystal is more stable. Left, experimental result for a single disorder instance; right, numerical simulations. The top panels show the individual spin magnetizations as a function of time, and the bottom panels shows the Fourier transforms to the frequency domain.
Extended Data Figure 4 Finite size scaling.
Shown are subharmonic central peak heights as a function of the perturbation, for different numbers of ions, N = 10, 12, and 14. We observe a sharpening, that is, that the curvature of the slope is increasing, as the chain size grows, consistent with expectations. Each curve contains one disorder realization, which is a single sample of random instance with W0t3 = π, but the data are averaged over all the ions (yielding the error bars shown). Inset, phenomenological scaling collapse of the three curves10, with the following parameters: εc = 0.041, v = 0.33, β = 1.9, which are critical exponents following the analysis in ref. 10. The extracted value of εc is consistent with the interaction strength, which is fixed at 2J0t2 = 0.048 throughout this dataset.
Extended Data Figure 5 Different initial states.
Starting with the left half of the chain initialized in the opposite direction, we observe that the time crystal is still persistent in the presence of perturbations. Top left, time-dependent magnetizations for ions in the first half of the chain. Bottom left, magnetizations for the second half. Notice that the spins on the two halves oscillate with opposite phases throughout, until the end of the evolution. Right, average peak height as a function of perturbation. Inset, FFT spectrum for 2% perturbation. 2J0t2 was fixed at 0.048 throughout this dataset.
Extended Data Figure 6 A random sampling from numerical evolutions.
Shown are averages of 10 disorder instances from numerical evolution under H for 2J0t2 = 0.072. Left, an example random numerical dataset (points) and the fit to equation (3) in Methods (dashed line). Right, the normalized probability distribution (PDF) of peak fit centres εp is shown in yellow, and a normal distribution is overlaid in red. The normal distribution is fitted using only the mean and standard deviation of the sample, showing excellent agreement with Gaussian statistics. For this value of J0 the mean  and the standard deviation σεp = 0.006.
and the standard deviation σεp = 0.006.
Rights and permissions
About this article
Cite this article
Zhang, J., Hess, P., Kyprianidis, A. et al. Observation of a discrete time crystal. Nature 543, 217–220 (2017). https://doi.org/10.1038/nature21413
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature21413
This article is cited by
-
Quantum many-body simulations on digital quantum computers: State-of-the-art and future challenges
Nature Communications (2024)
-
Programmable Heisenberg interactions between Floquet qubits
Nature Physics (2024)
-
Robust continuous time crystal in an electron–nuclear spin system
Nature Physics (2024)
-
Eigenstate properties of the disordered Bose–Hubbard chain
Frontiers of Physics (2024)
-
A von-Neumann-like photonic processor and its application in studying quantum signature of chaos
Light: Science & Applications (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.