Abstract
Classical to quantum decoherence transition, an issue existing for incoherent superposition of Bell-diagonal states is studied for three dimensional bipartite AB mixed quantum systems. Depending on the initial conditions, the dynamics of classical and quantum correlations can exhibit a sudden transition between classical to quantum decoherence. This result is calculated numerically by using entropic and geometric measures of correlations. An alternative explanation for this effect could be obtained by extending the bipartite A ⊗ B qutrit system to a pure tripartite A ⊗ B ⊗ C system. The freezing of classical correlations in AB is related to a freezing of the entanglement in the AC bipartition.
Similar content being viewed by others
Introduction
Quantum correlations have proven to be an essential resource for quantum computation and quantum information processing tasks. Entanglement has been extensively studied from a theoretical1,2 and an experimental point of view3,4,5. Entangled states have allowed to improve and develop a great variety of information protocols, such as, quantum key distribution6,7, quantum dense coding8,9 quantum teleportation10,11, entanglement swapping12, quantum repeaters13, among others. However, in recent years it has been realized that other quantum correlations than entanglement could play a central role in the development of quantum information processing, such as quantum discord (QD)14,15,16,17, defined as the difference between all correlations available in the system and the maximum of classical correlations15, or the closest distance between a quantum and its respective classical state16,17. It has been proved that states with non-zero QD are more efficient than entangled states in the performance of Knill-Laflamme algorithm18,19, quantum cryptography20, quantum state broadcasting21, quantum state discrimination22, and as an indicator of quantum phase transition23.
Realistic quantum systems are always interacting with their environment, inducing unavoidable decoherence processes. Quantum discord has proven to be more robust than entanglement under the action of a Markovian environment24. On the other hand, for non-dissipative decoherence channels, incoherent superpositions of Bell states can exhibit freezing dynamics25,26. In particular for some specific initial states a sudden transition between classical to quantum decoherence can happen25. As classical correlations decay, quantum correlations remain constant, until a time where this behavior is exchanged. The existence of this freezing dynamics has been experimentally observed in a variety of systems, such as, photons27, solid states systems28, and nuclear magnetic resonance29. From an entropic point of view, the evaluation of quantum discord is a difficult task, even for two-qubit states, since an optimization procedure is required for the conditional entropy over all local measurements. In this scenario, closed expressions are known only for specific classes of two qubit states30,31. While qubits are the essential ingredient in quantum information, nature is not restricted only to two dimensions. All these fundamental issues can be extended beyond qubits. Quantum discord in higher dimensions has been elusive, and little is known about calculations beyond two dimensional systems32,33,34,35,36.
In this work we address the study of quantum correlations other than entanglement for 3 ⊗ 3-dimensional bipartite mixed quantum systems. To accomplish this goal we consider both entropic and geometric measures of quantum correlations in order to verify our findings. Specifically we focus on the issue of classical to quantum decoherence transition in a system of two qutrits evolving under a dephasing environment. As the main result of this research we found that a sudden transition between classical to quantum decoherence exist for an initial superposition of maximally entangled qutrit states. The calculations are carried out by using entropic and geometric definitions of quantum correlations. In addition these results are studied using the Koashi-Winter37 relation, by extending the mixed 3 ⊗ 3 state to an enlarged pure 3 ⊗ 3 ⊗ n system. Entanglement embodied in a 3 ⊗ n bipartition is related with the classical correlations in the 3 ⊗ 3 bipartition.
Model
Consider a pair of three dimensional systems each one of them being described in a Hilbert space {|0〉, |1〉, |2〉}. We assume that each qutrit system is undergoing an interaction with a non dissipative environment introducing dephasing on quantum states. A general description of dephasing could even consider collective dephasing. Under such conditions we are mainly interested in studying the evolution of a superposition of maximally entangled two qutrit states given by:

where m = 0, 1, 2. Under a non dissipative environment, which is the situation we are mainly interested, the dynamics of entangled qutrit states can be studied considering both local and collective dephasing channels. The time evolution of the system, initially prepared in a state ρ(0), can be given in terms of Krauss Operators38, which preserves the trace and the positivity  . The dynamic of the system could be written as
. The dynamic of the system could be written as

where the Krauss Operators EA, FB and DAB describe the local and collective depolarizing noise, respectively. These operators have been studied by Ali39, and they are defined as

where  ,
,  , being ΓA,B the local dephasing rates, and
, being ΓA,B the local dephasing rates, and  ,
,  ,
,  . Here Γ2 is the collective depolarizing noise rate and
. Here Γ2 is the collective depolarizing noise rate and  ,
,  , and finally
, and finally  .
.
We are interested in exploring the effects of dephasing channels affecting qutrits in a superposition:

where c1 + c2 + c3 = 1. By considering ρ0 as the initial state with the following basis {|2, 2〉, |2, 1〉, |2, 0〉, |1, 2〉, |1, 1〉, |1, 0〉, |0, 2〉, |0, 1〉, |0, 0〉}, we obtain that the state evolves to:

where we have defined λ1 = (γAγB)2,  ,
,  and λ4 = γAγB. In what follows we will assume in most of the calculations equal dephasing rates for each qutrit, that is
and λ4 = γAγB. In what follows we will assume in most of the calculations equal dephasing rates for each qutrit, that is  with Γ1 being the local dephasing rate, and
with Γ1 being the local dephasing rate, and  with Γ2 being a collective dephasing rate.
with Γ2 being a collective dephasing rate.
Correlation Measure and Simulated Annealing Algorithm
We focus on the study of classical and quantum correlations for the model introduced in the previous section for different dephasing rates and initial conditions. The correlations dynamics will be studied by using both entropic and geometric measures of correlations. From an entropic point of view, quantum correlations embodied in a two qutrit mixed quantum state are given by15:

where  is the quantum mutual information and
is the quantum mutual information and  are the classical correlations, where S(ρA|B) is the conditional entropy obtained as the average of the von Neumann entropy of the reduced state of subsystem A after measuring subsystem B, and optimized with respect to all possible measurement on subsystem B. An alternative definition for classical and quantum correlation are given by the geometrical measurement16. In such case quantum correlations are defined by:
are the classical correlations, where S(ρA|B) is the conditional entropy obtained as the average of the von Neumann entropy of the reduced state of subsystem A after measuring subsystem B, and optimized with respect to all possible measurement on subsystem B. An alternative definition for classical and quantum correlation are given by the geometrical measurement16. In such case quantum correlations are defined by:

where the optimization is carried out with respect to all possible classical states χ. Let us represent by χAB the classical state that minimize  . The classical correlations from a geometrical view are given by:
. The classical correlations from a geometrical view are given by:

where the optimization is carried out with respect to all possible product states π. Thus the closest product state is πAB.
As is clear from definitions, both geometrical and entropic measures rely on an optimization process which requires to find the optimal value of a functional. For the entropic definition the optimization is over the all possible measurement on subsystem B, which requires to cover all possible projections  where l = 0, 1, 2 and VB is a unitary 3 × 3 matrix. There is one set of projections which optimize the conditional entropy given by an specific unitary VB. In the case of geometric definitions, we have to find the optimal distance
where l = 0, 1, 2 and VB is a unitary 3 × 3 matrix. There is one set of projections which optimize the conditional entropy given by an specific unitary VB. In the case of geometric definitions, we have to find the optimal distance  or
or  among all the classical and product states, respectively. We need to sample all the classical states to find χAB. This can be accomplished by defining an auxiliary classical state as:
among all the classical and product states, respectively. We need to sample all the classical states to find χAB. This can be accomplished by defining an auxiliary classical state as:

where |i〉 are the states of the composite qutrit basis, dc corresponds to the total dimension of the bipartite Hilbert space. We can associate each matrix element to square coordinates of unitary dc-sphere. Thereby the matrix elements Xi can be written as:


where  , ϕ0 = π/2 and
, ϕ0 = π/2 and  . To sample all the classical states we need to apply local arbitrary unitary transformations to each subsystem, in this way, the general classical state can be written as
. To sample all the classical states we need to apply local arbitrary unitary transformations to each subsystem, in this way, the general classical state can be written as

To build the product state, the procedure is slightly different, in this case, the auxiliary product state must be

where Xα (α = A, B) can be built in the same way that the matrix X, Eq. (9), with the difference that dc = 3 for the subsystem A and B and |i〉 is the qutrit basis. To sample all the product states we have to apply local arbitrary unitary transformations to each subsystem A and B. Then, the product state will be:

As we have learned from previous discussion to calculate quantum and classical correlations we must find an optimum among a set of states which can be sampled covering this set by arbitrary unitary matrices. In order to accomplish this goal we utilize the Simulated Annealing Algorithm (SAA)40 which has been used to calculate entanglement in higher dimensional systems41. To sample an arbitrary unitary matrix  and find the one that optimize a given functional
and find the one that optimize a given functional  , the conditional entropy or the distance, we need an algorithm that allows us to find a parametrization of the matrix elements of such unitary matrix. As is well known, an arbitrary unitary M × M matrix can be decomposed as the product of M(M − 1)/2 unitary operations42
, the conditional entropy or the distance, we need an algorithm that allows us to find a parametrization of the matrix elements of such unitary matrix. As is well known, an arbitrary unitary M × M matrix can be decomposed as the product of M(M − 1)/2 unitary operations42

where  and
and  . Each matrix
. Each matrix  can be parametrized in terms of three arbitrary parameters such that
can be parametrized in terms of three arbitrary parameters such that  ,
,  ,
,  and
and  42. Thus we have
42. Thus we have

Tipically for 3 × 3 dimension, the unitary transformation Vα (α = A, B) has the following form

A general unitary matrix  depends on 3(M − 1)M/2 arbitrary parameters belonging to [0, 2π]. Thus, for a bipartite 3 ⊗ 3-dimensional system, the classical and quantum correlations can be obtained by parametrizing Πl by dE = 9 angles for the entropic definition. On the other hand, for the geometrical measure, the arbitrary classical states in bipartite 3 ⊗ 3-dimensional systems can be parametrized by dχ = 26 angles. In addition, the general product state can be parametrized by dπ = 22 angles.
depends on 3(M − 1)M/2 arbitrary parameters belonging to [0, 2π]. Thus, for a bipartite 3 ⊗ 3-dimensional system, the classical and quantum correlations can be obtained by parametrizing Πl by dE = 9 angles for the entropic definition. On the other hand, for the geometrical measure, the arbitrary classical states in bipartite 3 ⊗ 3-dimensional systems can be parametrized by dχ = 26 angles. In addition, the general product state can be parametrized by dπ = 22 angles.
The sampling of all general unitary matrices for calculating quantum correlation using entropic definitions, or the sampling of all classical or product states for calculating quantum correlations using geometrical definitions is suitable for the application of the SAA algorithm40. The algorithm relies on a random choice of the parameter string  (where β = E, χ, or π), and changes the configuration according to the SAA as follows: (a) Choose any sufficiently large initial value
(where β = E, χ, or π), and changes the configuration according to the SAA as follows: (a) Choose any sufficiently large initial value  of
of  ; (b) choose at random an initial selection of
; (b) choose at random an initial selection of  , and save it; (c) change at random one of the dβ components of
, and save it; (c) change at random one of the dβ components of  , evaluate
, evaluate  and calculate the new
and calculate the new  for
for  ; (d) if
; (d) if  is less than the initial
is less than the initial  , accept the new configuration of
, accept the new configuration of  and start the algorithm again at (c); (e) if the calculated value
and start the algorithm again at (c); (e) if the calculated value  of the
of the  is greater than the initial
is greater than the initial  , select a random number
, select a random number  (
( ) and compare it with
) and compare it with  (for a conveniently chosen value of C). If
(for a conveniently chosen value of C). If  , accept the new configuration for
, accept the new configuration for  and start the algorithm again at (c). If
and start the algorithm again at (c). If  , reject the new configuration for
, reject the new configuration for  and start the algorithm again at c). Parameter C used above plays the role of a temperature. It has to be reduced according to a prescribed relation in order to resemble absolute zero and it also gives the possibility of accepting a configuration with a higher
and start the algorithm again at c). Parameter C used above plays the role of a temperature. It has to be reduced according to a prescribed relation in order to resemble absolute zero and it also gives the possibility of accepting a configuration with a higher  , preventing the system from being trapped in a local minimum.
, preventing the system from being trapped in a local minimum.
Results and Discussions
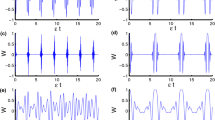
Let us consider in a first instance a bipartite qutrit system evolution under local dephasing. The general evolution in this situation is given in Eq. (5) for the case of independent dephasing environment where  and Γ2 = 0. Consider the case where we superpose two maximally entangled states of two qutrits, resembling the case of two qubits25, by choosing the amplitudes c1 and c2 as c1 = (1 + c)/2 and c2 = (1 − c)/2. In Fig. (1) we show the results for classical and quantum correlations calculated for the entropic and the geometric definition, using the SAA algorithm for the particular value c = 0.6. The existence of a sudden transition between classical to quantum decoherence is clearly observed, as compared with the situation in two qubit Bell-diagonal states. Geometric and entropic approach are coincident describing this behavior for this case.
and Γ2 = 0. Consider the case where we superpose two maximally entangled states of two qutrits, resembling the case of two qubits25, by choosing the amplitudes c1 and c2 as c1 = (1 + c)/2 and c2 = (1 − c)/2. In Fig. (1) we show the results for classical and quantum correlations calculated for the entropic and the geometric definition, using the SAA algorithm for the particular value c = 0.6. The existence of a sudden transition between classical to quantum decoherence is clearly observed, as compared with the situation in two qubit Bell-diagonal states. Geometric and entropic approach are coincident describing this behavior for this case.
Unlike the case of two qubits, little can be said from an analytical point of view to describe this transition in qutrit systems. However, an alternative way to calculate the classical correlations could be of help to understand and verify this result. This could be accomplished by considering the Koashi-Winter relation for entanglement and classical correlations embodied in a tripartite pure quantum state37. Consider a tripartite quantum system described by a pure state  , see Fig. (2). Entanglement and classical correlation among bipartitions are related as:
, see Fig. (2). Entanglement and classical correlation among bipartitions are related as:

where  stand for the classical correlations among the AB subsystems. The arrow indicates measurements that are carried out on system B. In order to use this relation, we have to transform the state given by Eq. (5) into a pure state, this can be carried out by extending the state to a larger Hilbert space. To illustrate this, we consider the case for c3 = 0 and local dephasing, that is Γ2 = 0, i.e.
stand for the classical correlations among the AB subsystems. The arrow indicates measurements that are carried out on system B. In order to use this relation, we have to transform the state given by Eq. (5) into a pure state, this can be carried out by extending the state to a larger Hilbert space. To illustrate this, we consider the case for c3 = 0 and local dephasing, that is Γ2 = 0, i.e.  ,
,  , and
, and  . After some manipulations we can write the state as:
. After some manipulations we can write the state as:

where we defined the states


From the expression (19) we immediately infer that ρ can be purified to a 3 ⊗ 3 ⊗ 7 dimensional Hilbert space. We denote this purification as ABC.
The Koashi-Winter relation states that the classical correlations in a AB bipartition are connected to the entanglement in a AC bipartition. Such connection has been useful to calculate entanglement in 2 ⊗ N systems that can be obtained from pure tripartite 2 ⊗ 2 ⊗ N systems43. In order to use this relation let us consider the 3 ⊗ (3 ⊗ 7) partition:

where  are entangled stated states in the 3 ⊗ 7 bipartition, p0 = p1 = p2 = 1/3 and
are entangled stated states in the 3 ⊗ 7 bipartition, p0 = p1 = p2 = 1/3 and

where the |ei〉 with i = 1, 2, … 7 are the states in the purification space.
The state (22) can be considered as a pure state decomposition of an entangled mixed state in the 3 ⊗ 7 (AC) bipartition. The entanglement in the 3 ⊗ 7 mixed state, will give us information about the classical correlations embodied in the 3 ⊗ 3 (AB) bipartition. Entanglement in 3 ⊗ 7 can be calculated by using the Simulated Annealing Algorithm (SAA)41. This is carried out searching for all pure state decompositions  of AC bipartition, applying an arbitrary unitary operation on the first qutrit of the state given in (22). The Entanglement EAC of the AC bipartition would be given by the decomposition that minimize
of AC bipartition, applying an arbitrary unitary operation on the first qutrit of the state given in (22). The Entanglement EAC of the AC bipartition would be given by the decomposition that minimize  , where
, where  is the von Neumann entropy of the reduced density matrix
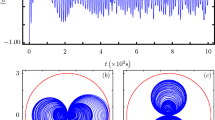
is the von Neumann entropy of the reduced density matrix  . In Fig. (3) we show the entanglement evolution in the 3 ⊗ 7 bipartition (EAC), the corresponding von Neumann entropy for reduced state of the qutrit (SA = log2 3), and the classical correlation for the 3 ⊗ 3 bipartition (
. In Fig. (3) we show the entanglement evolution in the 3 ⊗ 7 bipartition (EAC), the corresponding von Neumann entropy for reduced state of the qutrit (SA = log2 3), and the classical correlation for the 3 ⊗ 3 bipartition ( ), calculated through the Koashi-Winter expression. This result is in complete agreement with the calculation of the entropic and geometric measures for 3 ⊗ 3 system in (Fig. 1). Entanglement EAC is transfered from the AB bipartition up to a time tc where it became constant, given that SA is constant, the classical correlation in the AB became constant. This is an independent verification of the sudden transition between classical to quantum decoherence as given in Fig. (1). Entanglement freezing in the AC bipartition explain the freezing of classical correlations in AB bipartition.
), calculated through the Koashi-Winter expression. This result is in complete agreement with the calculation of the entropic and geometric measures for 3 ⊗ 3 system in (Fig. 1). Entanglement EAC is transfered from the AB bipartition up to a time tc where it became constant, given that SA is constant, the classical correlation in the AB became constant. This is an independent verification of the sudden transition between classical to quantum decoherence as given in Fig. (1). Entanglement freezing in the AC bipartition explain the freezing of classical correlations in AB bipartition.
Simulated Annealing calculation of entanglement EAC for 3 ⊗ 7 (AC) bipartition, and the corresponding classical correlations for the 3 ⊗ 3 (AB) bipartition, using the Koashi-Winter relation for the state in Fig. (1).
The amount of classical correlation where the AB partition system saturates depend on the value of c. The maximum corresponding to c = 1 is equal to 1.5850 and the minimum value is 0.5850 for c = 0. The last case occurs for the initial balanced amplitudes c1 = c2 = 1/2, see Fig. (4). We can calculate numerically the amount of maximal entanglement transferred to the AC bipartition which is the entanglement embodied in the state

where  are the states (23) for large times
are the states (23) for large times

The maximal entanglement EAC as a function of c is shown in Fig. (5). We observe that for c = 1 no entanglement is obtained between the AC bipartition as can be understood immediately from Eq. (4) for c2 = c3 = 0. The maximum entanglement transferred to AC corresponds to the balanced state with c1 = c2 = 1/2. The corresponding times for which the sudden transition happens are shown in Fig. (6).
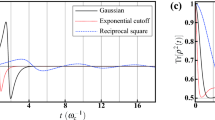
Considering global dephasing in addition to local dephasing, the issue of sudden transition between classical to quantum decoherence is still present along the dynamics of the AB system as can be seen in Fig. (7a). We observe that the amount of initial quantum correlation decreases as we spread the probability among states belonging to a wider Hilbert subspace. This reduction is enhanced as we approach to a balanced superposition, as we can see in (7.b). In all the cases we see that classical correlations maintain their decay behaviour until it suddenly becomes constant. This behavior can be verified in the same way as we did for the first case analyzed, by using the Koashi-Winter relation. However, quantum correlations increases because of the global dephasing until they start to decay. The same increment was observed in the presence of multilocal environments in bipartite qubit-qutrit systems36.
Classical and quantum correlation under the action of noisy channels as a function of Γ1t for two different initial condition (a,b) for the same dephasing rates. Due to the global dephasing channel the quantum correlation suffer a revival until the critical time. The dots are obtained by using geometrical measure. The continuous line are calculated by entropic measure.
As a final remark we mention a recent work where time invariant quantum discord has been obtained for an special class of qubit-qutrit states44. Such situation appears when the qubit is protected from the environment. We consider the situation when one of our qutrits is protected, assuming, for example ΓA = 1 and ΓB = 0 in equation (5), for the kind of initial states we are studying. Figure (8) illustrates the quantum correlations of the qutrit systems without global dephasing (see Fig. (8a)) and with global dephasing (see Fig. (8b)). We observe in Fig. (8) that the sudden transition between classical to quantum decoherence is still present for the case when one qutrit is protected. An interesting issue should be to investigate whether or not there is class of entangled qutrit states that could exhibit time invariant quantum discord.
Classical and quantum correlation under the action of noisy channels as a function of ΓAt for two different initial conditions without global dephasing (a) and with global dephasing (b). We have considered one qutrit protected from local dephasing, i.e., ΓB = 0. The dots are obtained by using the geometrical measure. The continuous line are calculated by the entropic measure.
For the entropic definition, we have changed the annealing parameter as C = 10−910−k, where k = [1, K], and K is the number of annealing processes. For every figure in this work we used K = 10, with 105 iterations for each k and Δϕ = 0.0125. For the geometric definition, we have changed the annealing parameter for the classical correlation (quantum correlation) as C = 10−510−k (C = 10−610−k) where k = [1, K]. For this case we used K = 20, with 105 iterations for each k and Δϕ = 0.01. Each point has been calculated independently, where most of the points converges to the first seed.
Conclusions
In summary, we have addressed the calculation of quantum and classical correlations for incoherent superpositions of maximally entangled qutrit states. We have carried out the calculation by using the simulated annealing algorithm, which is simple to implement and provides an efficient numerical approach. We focused on the issue of classical to quantum decoherence transition in a system of two qutrits evolving under a dephasing environment. As the main result of this research, we have found that a sudden transition between classical to quantum decoherence exist for an initial superposition of maximally entangled qutrit states. This freezing is intimately linked to the Entanglement freezing between one qutrit and the environment, as confirmed by using the Koashi-Winter expression. The amount of classical correlation saturation is limited by this entanglement. In addition, we have observed that the sudden transition between classical to quantum decoherence is still present for the case when one qutrit is protected. We have used the entropic and geometric measures of correlations, both describing the same behavior. These results can be of help to enhance the study of quantum discord and classical correlations in higher dimensions and for the implementation of quantum information processing protocols.
Additional Information
How to cite this article: Cárdenas-López, F. A. et al. Sudden Transition between Classical to Quantum Decoherence in bipartite correlated Qutrit Systems. Sci. Rep. 7, 44654; doi: 10.1038/srep44654 (2017).
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
Horodecki, R., Horodecki, P., Horodecki, M. & Horodecki, K. Quantum entanglement. Rev. Mod. Phys. 81, 865–942 (2009).
Gühne, O. & Tóth, G. Entanglement detection. Phys. Rep. 474, 1–75 (2009).
Walborn, S. P., Souto Ribeiro, P. H., Davidovich, L., Mintert, F. & Buchleitner, A. Experimental determination of entanglement with a single measurement. Nature 440, 1022–1024 (2006).
Almeida, M. P. et al. Environment-induced sudden death of entanglement. Science 316, 579–582 (2007).
Laurat, J., Choi, K. S., Deng, H., Chou, C. W. & Kimble, H. J. Heralded entanglement between atomic ensembles: Preparation, decoherence, and scaling. Phys. Rev. Lett. 99, 180504 (2007).
Ekert, A. K. Quantum cryptography based on bell’s theorem. Phys. Rev. Lett. 67, 661–663 (1991).
Tittel, W., Brendel, J., Zbinden, H. & Gisin, N. Quantum cryptography using entangled photons in energy-time bell states. Phys. Rev. Lett. 84, 4737–4740 (2000).
Bennett, C. H., Brassard, G. & Mermin, N. D. Quantum cryptography without bell’s theorem. Phys. Rev. Lett. 68, 557–559 (1992).
Mattle, K., Weinfurter, H., Kwiat, P. G. & Zeilinger, A. Dense coding in experimental quantum communication. Phys. Rev. Lett. 76, 4656–4659 (1996).
Bennett, C. H. et al. Teleporting an unknown quantum state via dual classical and einstein-podolsky-rosen channels. Phys. Rev. Lett. 70, 1895–1899 (1993).
Bouwmeester, D. et al. Experimental quantum teleportation. Nature 390, 575–579 (1997).
Yurke, B. & Stoler, D. Einstein-podolsky-rosen effects from independent particle sources. Phys. Rev. Lett. 68, 1251–1254 (1992).
Dür, W., Briegel, H.-J., Cirac, J. I. & Zoller, P. Quantum repeaters based on entanglement purification. Phys. Rev. A 59, 169–181 (1999).
Henderson, L. & Vedral, V. Classical, quantum and total correlations. J. Phys. A: Math. Gen. 34, 6899 (2001).
Ollivier, H. & Zurek, W. H. Quantum discord: A measure of the quantumness of correlations. Phys. Rev. Lett. 88, 017901 (2001).
Modi, K., Paterek, T., Son, W., Vedral, V. & Williamson, M. Unified view of quantum and classical correlations. Phys. Rev. Lett. 104, 080501 (2010).
Modi, K., Brodutch, A., Cable, H., Paterek, T. & Vedral, V. The classical-quantum boundary for correlations: Discord and related measures. Rev. Mod. Phys. 84, 1655–1707 (2012).
Datta, A., Shaji, A. & Caves, C. M. Quantum discord and the power of one qubit. Phys. Rev. Lett. 100, 050502 (2008).
Lanyon, B. P., Barbieri, M., Almeida, M. P. & White, A. G. Experimental quantum computing without entanglement. Phys. Rev. Lett. 101, 200501 (2008).
Pirandola, S. Quantum discord as a resource for quantum cryptography. Sci. Rep. 4, 6956 (2014).
Piani, M., Horodecki, P. & Horodecki, R. No-local-broadcasting theorem for multipartite quantum correlations. Phys. Rev. Lett. 100, 090502 (2008).
Roa, L., Retamal, J. C. & Alid-Vaccarezza, M. Dissonance is required for assisted optimal state discrimination. Phys. Rev. Lett. 107, 080401 (2011).
Werlang, T., Trippe, C., Ribeiro, G. A. P. & Rigolin, G. Quantum correlations in spin chains at finite temperatures and quantum phase transitions. Phys. Rev. Lett. 105, 095702 (2010).
Werlang, T., Souza, S., Fanchini, F. F. & Villas Boas, C. J. Robustness of quantum discord to sudden death. Phys. Rev. A 80, 024103 (2009).
Mazzola, L., Piilo, J. & Maniscalco, S. Sudden transition between classical and quantum decoherence. Phys. Rev. Lett. 104, 200401 (2010).
Maziero, J., Céleri, L. C., Serra, R. M. & Vedral, V. Classical and quantum correlations under decoherence. Phys. Rev. A 80, 044102 (2009).
Xu, J.-S. et al. Experimental investigation of classical and quantum correlations under decoherence. Nat. Commun. 1, 7 (2010).
Rong, X. et al. Experimental protection and revival of quantum correlation in open solid systems. Phys. Rev. B 88, 054419 (2013).
Maziero, J. et al. Quantum discord in nuclear magnetic resonance systems at room temperature. Braz. J. Phys. 43, 86–104 (2013).
Luo, S. Quantum discord for two-qubit systems. Phys. Rev. A 77, 042303 (2008).
Ali, M., Rau, A. R. P. & Alber, G. Quantum discord for two-qubit X states. Phys. Rev. A 81, 042105 (2010).
Chitambar, E. Quantum correlations in high-dimensional states of high symmetry. Phys. Rev. A 86, 032110 (2012).
Karpat, G. & Gedik, Z. Correlation dynamics of qubit-qutrit systems in a classical dephasing environment. Phys. Lett. A 375, 4166–4171 (2011).
Ali, M. Quantum discord for a two-parameter class of states in 2 ⊗ d quantum systems. J. Phys. A: Math. Theor. 43, 495303 (2010).
Khan, S. & Khan, M. K. Nondistillability of distillable qutrit–qutrit states under depolarising noise. J. Mod. Opt. 58, 918–923 (2011).
Khan, S. & Ahmad, I. Environment generated quantum correlations in bipartite qubit-qutrit systems. Optik 127, 2448–2452 (2016).
Koashi, M. & Winter, A. Monogamy of quantum entanglement and other correlations. Phys. Rev. A 69, 022309 (2004).
Kraus, K. States, Effect, and Operations: Fundamental Notions in Quantum Theory (Springer-Verlag, Berlin, 1983).
Ali, M. Distillability sudden death in qutrit-qutrit systems under global and multilocal dephasing. Phys. Rev. A 81, 042303 (2010).
Van Laarhoven, P. J. & Aarts, E. H. Simulated annealing: Theory and applications (D. Reidel Publishing Company, Dordrecht, Holland, 1987).
Allende, S., Altbir, D. & Retamal, J. C. Simulated annealing and entanglement of formation for (n ⊗ m) -dimensional mixed states. Phys. Rev. A 92, 022348 (2015).
Nielsen, M. A. & Chuang, I. L. Quantum computation and quantum information (Cambridge University Press, UK, 2000).
Lastra, F., López, C. E., Roa, L. & Retamal, J. C. Entanglement of formation for a family of (2 ⊗ d) -dimensional systems. Phys. Rev. A 85, 022320 (2012).
Karpat, G. & Gedik, Z. Invariant quantum discord in qubit–qutrit systems under local dephasing. Phys. Scripta 2013, 014036 (2013).
Acknowledgements
We acknowledge financial support from Financiamiento Basal para Centros Cientficos y Tecnológicos de Excelencia grant FB 0807, Fondecyt 1140194 and 1161018. F.A.C. acknowledge to VRIDEI.
Author information
Authors and Affiliations
Contributions
F.A.C.-L., S.A. carried out numerical analysis and contributed to write the manuscript. S.A. prepared the figures, J.C. contributed to theoretical analysis and write the manuscript. All authors reviewed the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Cárdenas-López, F., Allende, S. & Retamal, J. Sudden Transition between Classical to Quantum Decoherence in bipartite correlated Qutrit Systems. Sci Rep 7, 44654 (2017). https://doi.org/10.1038/srep44654
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep44654
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.