Abstract
We propose a method to convert linearly polarized incident electromagnetic waves fed by a single source into multi-beam reflections with independent control of polarizations based on anisotropic metasurface at microwave frequencies. The metasurface is composed of Jerusalem Cross structures and grounded plane spaced by a dielectric substrate. By designing the reflection-phase distributions of the anisotropic metasurface along the x and y directions, the x- and y-polarized incident waves can be manipulated independently to realize multi-beam reflections. When the x- and y-polarized reflected beams are designed to the same direction with equal amplitude, the polarization state of the beam will be only controlled by the phase difference between the x- and y-polarized reflected waves. Three examples are presented to show the multi-beam reflections with flexible control of polarizations by using anisotropic metasurfaces and excellent performance. Particularly, we designed, fabricated, and measured an anisotropic metasurface for two reflected beams with one linearly polarized and the other circularly polarized. The measurement results have good agreement with the simulations in a broad bandwidth.
Similar content being viewed by others
Introduction
Metasurface is two-dimensional (2D) planar surfaces constructed by a series of metallic or dielectric structures with subwavelength scale on the interface of two media with different refractive indices. The metallic structures can introduce discontinuous phase shifts on the surface, hence the electromagnetic waves (or lights) impinging on the metasurface will interact with the metallic structures to generate anomalous refractions and reflections, which obey the generalized Snell law1. Due to the scattering of metallic structures on the interface, the wavefronts of lights or waves can be modified to realize the desired functional devices in the regions of optics2,3,4,5,6,7,8,9, terahertz10,11,12,13,14, microwave15,16,17,18,19,20, and acoustics21,22,23,24,25. Otherwise, a grating metasuface also can be designed to capture light efficiently into surface plasmons by using transformation optics26. The polarization plays an important role in manipulating the lights or electromagnetic waves, realizing polarization beam splitters9,18, quarter-wave plates7, polarization-controlled plasmonic couplers2, and polarization converters19. Many efforts have been made to manipulate the polarizations by using metamaterials27,28,29 and metasurfaces30,31,32,33,34,35,36,37,38. However, these polarization modulations are mostly concentrated on a single radiation beam.
In this work, we propose a method to realize multi-beam reflections with independent control of polarizations based on anisotropic metasurfaces. The metasurfaces are composed of Jerusalem Cross structures and a grounded plane spaced by a dielectric substrate. A Ku-band coax-to-waveguide device is placed in front of the metasurfaces used as the feeding source, which can generate quasi-spherical incident waves with linear polarization39. The quasi-spherical incident waves can be reflected by the metasurfaces with high efficiency, while the reflected phases of x- and y-polarized waves can be controlled independently by changing the dimensions of the I-shaped structures on x and y directions, respectively. Based on the compensation method of geometrical optics and superposition of aperture fields, the x- and y-polarized reflected waves can be converted into multi-beam reflections independently with high directivities. In particular, when the x- and y-polarized waves are reflected to the same direction with equal amplitude, the polarization state of each reflected beam can be controlled independently by the phase difference between the x- and y-polarized reflected waves. Three full-wave simulation examples with single, dual and six reflected beams manipulated by anisotropic metasurfaces for both x- and y-polarized waves are provided to verify the proposed method, and the simulation results show good abilities of the designed metasurfaces in controlling the multi-beam reflections with independent control of polarization. For experimental verification, we design, fabricate and measure a metasurface, which can convert the incident quasi-spherical waves into two reflected beams with one linearly polarized and the other circularly polarized. The measured results demonstrate good performance of the designed metasurface, which has good agreement with the simulation.
Results
Theory and simulations
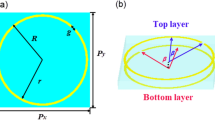
The model of the proposed anisotropic metasurface fed by a point source is illustrated in Fig. 1. We assume that the point source is located at the top of the metasurface with coordinates of (0, 0, R0), and the coordinate origin is defined in the geometrical centre of the metasurface, as shown in Fig. 1(a). Then we divide the metasurface into N × N pixels, in which one pixel is a unit cell of the metasurface. The reflected phase of each pixel can be designed by changing the dimensions of the unit cell. To focus the reflected waves into plane waves with a designed deflection angle, the required reflected phase of the pixel at the position of (xi, yi, 0) can be calculated according to the phase compensation of geometrical optics
The sketch of the multi-beam reflection with independent control of x- and y-polarized waves fed by a linearly polarized point source with v polarization in front of the anisotropic metasurfaces.
(a) The decomposed x- and y-polarized waves are reflected to the different directions. (b) The decomposed x- and y-polarized waves are reflected to the same directions.

in which Φ0(x0, y0) is the reflection phase at the origin of the coordinate, R0 and Ri are the distances between the feeding source and pixels of (0, 0, 0) and (xi, yi, 0), respectively, and (θk, φk) is the deflection angle of the reflected plane waves.
Hence, if we design an anisotropic metasurface, whose phase distributions in both x and y directions are designed independently according to Eq. (1), then the x- and y-polarized waves can be controlled and reflected independently to the directions of (θx, φx) and (θy, φy), respectively. Furthermore, both x- and y-polarized waves can also be designed to multi-beam reflections by using superposition of the aperture fields40,41. To generate M1 and M2 (M1 and M2 are positive real numbers) reflected beams for the x- and y-polarized waves, the reflection phases of the metasurface at position of (xi, yi, 0) for Ex and Ey components can be calculated as41


where  and
and  are the required phases at position of (xi, yi, 0) for the k1th and k2th reflected beams of the x- and y-polarized waves with the radiation directions of
are the required phases at position of (xi, yi, 0) for the k1th and k2th reflected beams of the x- and y-polarized waves with the radiation directions of  and
and  , respectively, which can be obtained from Eq. (1). We further define a new rectangular coordinate uvw by rotating original rectangular coordinate xyz 45° clockwise along the z axis, as shown in Fig. 1. Hence, when the incident waves are fixed by v polarization, then the total electric field of Ev can be decomposed to Ex and Ey with |Ex| = |Ey|, and then the x- and y-polarized waves can be controlled and reflected independently to the different directions as demonstrated in Fig. 1(a) or the same directions as demonstrated in Fig. 1(b). Particularly, when the x- and y-polarized waves are reflected to the same directions, the polarization state of each beam can be only controlled independently by the phase difference of
, respectively, which can be obtained from Eq. (1). We further define a new rectangular coordinate uvw by rotating original rectangular coordinate xyz 45° clockwise along the z axis, as shown in Fig. 1. Hence, when the incident waves are fixed by v polarization, then the total electric field of Ev can be decomposed to Ex and Ey with |Ex| = |Ey|, and then the x- and y-polarized waves can be controlled and reflected independently to the different directions as demonstrated in Fig. 1(a) or the same directions as demonstrated in Fig. 1(b). Particularly, when the x- and y-polarized waves are reflected to the same directions, the polarization state of each beam can be only controlled independently by the phase difference of  between x- and y-polarized reflected waves according to Eq. (1), where
between x- and y-polarized reflected waves according to Eq. (1), where  correspond to co-polarization, right-handed circular polarization, cross-polarization and left-handed circular polarization, respectively.
correspond to co-polarization, right-handed circular polarization, cross-polarization and left-handed circular polarization, respectively.
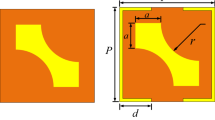
The metasurface, which is composed of a series of Jerusalem Cross structures and a grounded plane spaced by a dielectric substrate, has been proposed to realize above functions as shown in Fig. 2(a,b), in which the parameters are P = 6 mm, a = 1.8 mm, h = 2 mm, w = 0.2 mm, t = 0.018 mm and variables of lx and ly. The dielectric substrate is F4B with relative permittivity of 2.65 and tangent loss of 0.001. The incident waves are almost totally reflected by the metasurface at 15 GHz, but the reflected phases of Ex (Ey) can be manipulated from 70° to −230° by changing the length of lx (ly) independently, which will not affect the reflection phase of Ey (Ex) as shown in Fig. 2(c). The similar phase responses also can be achieved as the frequency changes from 13 GHz to 17 GHz as shown in Fig. 2(d). If a feeding source is placed in front of the metasurface with v polarization, then the incident waves are v-polarized waves, and the electric-field vector of Ev can be decomposed to Ex and Ey with |Ex| = |Ey|, so the x- and y-polarized waves can be controlled independently by phase distributions of the metasurface in x and y directions, respectively. We remark that the feeding source used in our simulations and experiments is a linearly polarized Ku-band (12 GHz–18 GHz) coax-to-waveguide device with nearly equal E- and H-plane radiation patterns39. In the following, three specific examples are investigated by simulations to show the powerful ability of the proposed anisotropic metasurfaces in multi-beam reflections with independent control of polarizations.
The unit cell of the anisotropic metasurface, and its amplitude and phase responses.
(a) The front view of the unit cell composed of two orthogonal I-shaped structures in x and y directions. The new coordinate system uvw is defined by rotating coordinate system xyz 45° clockwise along the z axis. (b) The side view of the unit cell, the Jerusalem Cross structure and grounded plane is spaced by a dielectric substrate. (c) The amplitude and phase responses of the unit cell under x- and y-polarized incident waves, respectively, by only changing the length of lx. (d) The phase responses of the x-polarized reflected waves from 13 GHz to 17 GHz by changing the length of lx.
We first consider that only one beam of both x- and y-polarized waves are reflected independently by the metasurface, whose phase distributions can be calculated from Eqs (2) and (3) by choosing M1 = M2 = 1 with the reflection directions of (θx, φx) and (θy, φy), respectively.


In which the Φx0 and Φy0 are the reflection phases at the origin of coordinate for x- and y-polarized waves, respectively, which can be the same or different.
The metasurface I is designed to reflect the x- and y-polarized waves to the different directions of (θx = 30°, φx = 315°) and (θy = 30°, φy = 135°) at 15 GHz as shown in Fig. 3(a,b), respectively. When the incident waves are fixed as v polarization, the x- and y-polarized waves can be separated and reflected independently to the directions of (30°, 315°) and (30°, 135°), respectively, as shown in Fig. 3(c). The metasurface II is designed to reflect the x- and y-polarized waves to the same direction of (θx = θy = 30°, φx = φy = 135°) at 15 GHz as shown in Fig. 3(e,f). When the incident waves are fixed as v polarization, both x- and y-polarized waves are reflected to the same direction of (30°, 135°) and combined to a single beam B, as illustrated in Fig. 3(f), and the polarization state of the beam can be controlled by ΔΦ = Φx0 − Φy0. Here, we design ΔΦ = 90° to generate a circularly polarized beam, whose axial ratios are smaller than 1.8 and the radiation angle of θ steers from 32.5° to 25.8° from 14 GHz to 17 GHz, as shown in Fig. 4.
One reflected x- and y-polarized beam manipulated independently by the metasurfaces.
(a–c) The x- and y-polarized waves are reflected to the different directions by the metasurface I: (a) the x-polarized waves are reflected to Bx (30°, 315°), (b) the y-polarized waves are reflected to By (30°, 135°), (c) the x- and y-polarized waves are separated and reflected to Bx (30°, 315°) and By (30°, 135°), respectively, for v-polarized incident waves. (d–f) The x- and y-polarized beams are reflected to the same direction by the metasurface II: (d) the x-polarized waves are reflected to Bx (30°, 135°), (e) the y-polarized waves are also reflected to By (30°, 135°), (f) the x- and y-polarized waves are reflected to the same direction of B (30°, 135°) for v-polarized incident waves.
The simulated beam deflections and axis ratios of the reflected beam shown in Fig. 3(f) from 14 GHz to 17 GHz.
We further consider that two beams of both x- and y-polarized waves are reflected independently by the metasurface, whose phase distributions can be calculated from Eqs (2) and (3) by choosing M1 = M2 = 2 respectively.


In which


where the  and
and  are the reflection phases at the origin of coordinate for the kth reflected beams of the x- and y-polarized waves, respectively, which can be the same or different.
are the reflection phases at the origin of coordinate for the kth reflected beams of the x- and y-polarized waves, respectively, which can be the same or different.
The metasurface III is designed to separate and reflect x-polarized waves to the directions of Bx1 (θx1 = 45°, φx1 = 315°) and Bx2 (θx2 = 30°, φx2 = 135°) as shown in Fig. 5(a), and the y-polarized waves to the directions of By1 (θy1 = 45°, φy1 = 225°) and By2 (θy2 = 30°, φy2 = 45°) as shown in Fig. 5(b). When the incident waves are fixed as v polarization, the x- and y-polarized waves can be separated and reflected independently to the different directions at same time, respectively, as shown in Fig. 5(c). The metasurface IV is also designed to separate both x- and y-polarized waves to two beams but deflected to the same directions of B1 (θ1 = 45°, φ1 = 315°) and B2 (θ2 = 30°, φ2 = 135°) as shown in Fig. 5(d,e), respectively. When the incident waves are fixed as v polarization, the x- and y-polarized waves also can be separated and reflected to two beams, but deflect to the same directions as shown Fig. 5(f). The polarization states of B1 and B2 can be manipulated independently by the phase differences between the x- and y-polarized waves for each beam, respectively. Here, we design  and
and  to realize circular and linear polarizations for B1 and B2, respectively. The simulated results show that the B1 and B2 are directed to 45° and 30° at 15 GHz, which are decreased from 49° to 41° and 32° to 28° as frequency increases from 14 GHz to 16.5 GHz, respectively, as red solid lines shown in Fig. 6. The axial ratios of B1 are lower than 2.5dB in whole frequency band to exhibit a good characteristic of circular polarization, and the axial ratios of B2 are larger than 25dB in whole frequency band to exhibit a good characteristic of linear polarization, as blue solid lines shown in Fig. 6.
to realize circular and linear polarizations for B1 and B2, respectively. The simulated results show that the B1 and B2 are directed to 45° and 30° at 15 GHz, which are decreased from 49° to 41° and 32° to 28° as frequency increases from 14 GHz to 16.5 GHz, respectively, as red solid lines shown in Fig. 6. The axial ratios of B1 are lower than 2.5dB in whole frequency band to exhibit a good characteristic of circular polarization, and the axial ratios of B2 are larger than 25dB in whole frequency band to exhibit a good characteristic of linear polarization, as blue solid lines shown in Fig. 6.
Two reflected x- and y-polarized beams manipulated by the metasurfaces.
(a–c) The x- and y-polarized waves are reflected to the different directions by the metasurface III: (a) the x-polarized waves are reflected to Bx1 (30°, 315°) and Bx2 (30°, 135°), (b) the y-polarized waves are reflected to By1 (30°, 45°) and By2 (30°, 225°), (c) the x-polarized waves are reflected to Bx1 (30°, 315°) and Bx2 (30°, 135°) and the y-polarized waves are reflected to By1 (30°, 45°) and By2 (30°, 225°) at the same time for v-polarized incident waves. (d–f) The x- and y-polarized waves are reflected to the same directions by the metasurface IV: (d) the x-polarized waves are reflected to Bx1 (30°, 315°) and Bx2 (30°, 135°), (e) the y-polarized waves are also reflected to By1 (30°, 315°) and By2 (30°, 135°), (f) the x- and y-polarized waves are reflected to the same directions of B1 (30°, 315°) and B2 (30°, 135°) at the same time for v-polarized incident waves.
The simulated beam deflections and axis ratios of the B1 and B2 shown in Fig. 5(f) from 14 GHz to 16.5 GHz.
We finally design the metasurface V to reflect six beams of both x- and y-polarized waves, respectively. Similarly, the phase distributions of the metasurface also can be calculated from Eqs (2) and (3) by choosing M1 = M2 = 6. Figure 7(a) shows that the x-polarized incident waves are separated to six beams with the directions of Bx1 (θx1 = 30°, φ1 = 45°), Bx2 (θx2 = 0, φx2 = 0), Bx3 (θx3 = 30°, φx3 = 225°), Bx4 (θx4 = 30°, φx4 = 90°), Bx5 (θx5 = 30°, φx5 = 135°) and Bx6 (θx6 = 30°, φx6 = 180°) after reflected by the metasurface. Figure 7(b) shows that the y-polarized incident waves are also separated to six radiation beams with the directions of By1 (θx1 = 30°, φy1 = 45°), By2 (θx2 = 0, φy2 = 0), By3 (θx3 = 30°, φy3 = 225°), By4 (θx4 = 30°, φy4 = 0), By5 (θx5 = 30°, φy5 = 315°) and By6 (θx6 = 30°, φy6 = 270°) after reflected by the metasurface. Hence, when the incident waves are fixed as v polarization, the x- and y-polarized waves can be manipulated independently by the metasurface at the same time to generate six reflected beams, respectively. However, because the Bx1, Bx2 and Bx3 of x-polarized waves are deflected to the same directions with the By1, By2 and By3 of y-polarized waves, and the beams are combined to B1, B2 and B3, respectively, as shown in Fig. 7(c), whose polarization states can be controlled independently by designing the phase differences of ΔΦ1, ΔΦ2 and ΔΦ3, respectively. Here, the ΔΦ1, ΔΦ2 and ΔΦ3 are designed to π/2, 0 and −π/2 to make B1, B2 and B3 right-handed circular polarization, linear polarization and left-handed circular polarization, respectively. The performance of each beam can be verified by calculating the axial ratios as above discussions, which are not provided here in consideration of the length of the paper.
Six reflected x- and y-polarized beams manipulated by metasurfaces.
(a) The x-polarized waves are separated and reflected to six different directions. (b) The y-polarized waves are separated and reflected to six different directions. (c) The x- and y-polarized waves are reflected to the six different directions at the same time for v-polarized incident waves, in which Bx1, Bx2 and Bx3 are reflected to the same directions with By1, By2 and By3 defined by B1, B2 and B3, respectively.
Experimental results
In experiments, we designed, fabricated and measured the metasurface IV, which can convert the incident x- and y-polarized waves into two reflected beams, respectively. The experimental sample is placed on a measurement platform, as demonstrated in Fig. 8(a), and the measured far-field patterns of v- and u-polarized reflected waves at 15 GHz are shown in Fig. 8(b). The measured results show that both v- and u-polarized waves are radiated to θ1 = −45° (beam 1) with nearly equal amplitude, but only the v-polarized waves are radiated to θ2 = 30° (beam 2). The measured amplitudes of both v- and u-polarized waves for beam 1 are about 3dB smaller than that of beam 2, which is because the beam 1 is designed to be a circular polarization with only half of the energy received by the linearly polarized receiving horn antenna in measurement. We also notice that the sidelobes are nearly 20dB smaller than the main beam of the beam 2, which is extremely low compared to the main beam. Hence, we can conclude that all the incident power is almost divided equally into the beam 1 and beam 2 with high radiation efficiency. In order to investigate the polarization of each beam, we measured the power distributions of E components for the beam 1 and beam 2 on the plane paralleling to their wavefronts, as shown by the black and red solid lines in Fig. 8(c), respectively. The measured results show good performances of the circular polarization for beam 1 and linear polarization for beam 2 at 15 GHz, respectively, which have a good agreement with the simulations, as shown in Fig. 5(f).
The experimental setup of metasurface IV and its measured results at 15 GHz.
(a) The metasurface IV fed by a Ku-band rectangular waveguide. (b) The measured far-field radiation patterns on uow plane for v and u polarizations, respectively. (c) The measured power distributions of B1 and B2 at 15 GHz, respectively, by rotating the receiving linearly polarized antenna 360° in the plane paralleling to its aperture.
The far-field patterns at 14.5 GHz, 15.5 GHz, 16 GHz and 16.5 GHz are also measured as shown in Fig. 9, which show good radiation performances except for slight deviations of beam 1 and beam 2 to the directions of −45° and 30°, respectively. Figure 10(a,c) are the measured power distributions of beam 1 and beam 2 in the plane paralleling to their wavefronts. Figure 10(b,d) are the normalized results of power distributions calculated by δR = 20(log|E|-log|Emin|), in which AR = max(δR) is the axis ratio of each beam. The axis ratios of beam 1 are smaller than 3dB at all frequencies as shown in Fig. 10(b), which demonstrate good performances of circular polarizations, and the axis ratios of beam 2 are larger than 20dB at all frequencies as shown in Fig. 10(d), which demonstrate good performances of linear polarizations. Hence, the working bandwidth of the designed metasurface can cover from 14.5 GHz to 16.5 GHz. We notice that the measured power becomes smaller and smaller as the frequency deviates further and further away from 15 GHz as shown in Fig. 10(a,c), this is because the main beams deviate away from the measured angles of −45° and 30° at these frequencies for beam 1 and beam 2, respectively.
The measured power distributions of B1 and B2 at different frequencies.
(a) The measured power distributions of B1, (b) the normalized power distributions of B1 calculated by δR = 20(log|E| − log|Emin|), (c) the measured power distributions of B2, (d) the normalized power distributions of B2 calculated by δR = 20(log|E| − log|Emin|).
Discussion
We have proposed a method based on the anisotropic metasurface to manipulate incoming quasi-spherical linearly polarized waves into multi-beam reflection with independent control of polarizations. The metasurface is composed of Jerusalem Cross structures and a grounded plane spaced by a dielectric substrate, which can control the x- and y-polarized reflected waves independently by designing the phase distributions in x and y directions, respectively. Particularly, when the x- and y-polarized reflected beams are reflected to the same direction, the polarization state of the beam can be controlled by designing the phase difference between the x- and y-polarized reflected waves. The full-wave simulated results verify that the reflected beams of x- and y-polarized waves can be manipulated independently, such as the number of beams, the reflection angles and polarization states. The metasurface, which can manipulate incoming quasi-spherical waves into two reflected beams with different polarizations, has been fabricated and measured, and the measured results have good agreement with the simulation. The proposed method in this paper provides a good choice for people to manipulate the reflected beams and their polarizations independently, which may have potential applications in satellite communications, millimetre wave image system, radar system and so on.
Methods
To design the metasurface IV, the required phase distributions of the metasurface for both Ex and Ey components at 15 GHz were first calculated from Eqs (6)–(9), in which the relative parameters are θx1 = θy1 = 45°, φx1 = φy1 = 315°, θx2 = θy2 = 30°, φx2 = φy2 = 135°, R0 = 91.8 mm,  and
and  . Then, the Jerusalem Cross structure with different lx and ly was chosen to realized the required Φxi and Φyi in each pixel of the metasurface according to the relationship between the dimension of the Jerusalem Cross structure and the reflected phase as demonstrated in Fig. 2(c).
. Then, the Jerusalem Cross structure with different lx and ly was chosen to realized the required Φxi and Φyi in each pixel of the metasurface according to the relationship between the dimension of the Jerusalem Cross structure and the reflected phase as demonstrated in Fig. 2(c).
The dimension of the designed metasurface is 306 mm × 306 mm with 51 unit cells in both x and y directions, which is fabricated by using printed circuit board (PCB) of F4B with relative permittivity of 2.65 and loss tangent of 0.001. In measurement, a Ku-band coax-to-waveguide device is placed in front of the metasurface as the feeding source to generate v-polarized quasi-spherical incident waves, and the distance between the feeding source and centre of the metasurface is 91.8 mm. A linearly polarized receiving horn antenna is placed in the other side of the anechoic chamber to receive the far-field power of the reflected waves by rotating the sample 360° in horizontal plane, as shown in Fig. 8(b). In order to investigate the polarization of each beam, we first rotate the sample by −45° in the horizontal plane to make the beam 1 be directed to the receiving horn. Then, we rotate the receiving horn by 360° in the plane parallel to its aperture with interval of 1° to measure the power distribution of E component for the beam 1, as shown by the black solid line in Fig. 8(c). The similar method also has also been used to measure the power distribution of E component for the beam 2, as shown by the red solid line in Fig. 8(c). We remark that the initial polarization (0 degree) of the receiving horn is the v polarization.
Additional Information
How to cite this article: Ma, H. F. et al. Multi-beam reflections with flexible control of polarizations by using anisotropic metasurfaces. Sci. Rep. 6, 39390; doi: 10.1038/srep39390 (2016).
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
Yu, N. et al. Light propagation with phase discontinuities: generalized laws of reflection and refraction. Science 334, 333–337 (2011).
Yin, X., Ye, Z., Rho, J., Wang, Y. & Zhang, X. Photonic spin hall effect at metasurfaes, Science 339, 1405–1407 (2013).
Lin, J. et al. Polarization-controlled tunable directional coupling of surface plasmon polaritons, Science 340, 331–334 (2013).
Huang. L. et al. Three-dimensional optical holography using a plasmonic metasurface, Nat. Commun. 3, 2155 (2013).
Aieta, F. et al. Aberration-free ultrathin flat lenses and axicons at telecom wavelengths based on plasmonic metasurfaces. Nano Lett. 12, 4932–4936 (2012).
Ni, X., Ishii, S., Kildishev, A. V. & Shalaev, V. M. Ultra-thin, planar, Babinetinverted plasmonic metalenses. Light Sci. Appl. 2, e72 (2013).
Yu, N. et al. A broadband, background-free quarter-wave plate based on plasmonic metasurfaces. Nano Lett. 12, 6328–6333 (2012).
Kildishev, A. V., Boltasseva, A. & Shalaev, V. M. Planar Photonics with Metasurfaces. Science 339, 1232009–1232009 (2013).
Farmahini-Farahani, M. & Mosallaei, H. Anisotropic reflectarray metasurface for beam engineering in infrared. Opt. Lett. 38, 462–464 (2013).
Liu, S. et al. Anisotropic coding metamaterals and their powerful manipulation of differently polarized terahertz waves. Light Sci. Appl. 5, e16076 (2016).
Gao, L. et al. Broadband diffusion of terahertz waves by multi-bit coding metasurfaces. Light Sci. Appl. 4, e324 (2015).
Liang, L. et al. Anomalous Terahertz Reflection and Scattering by Flexible and Conformal Coding Metamaterials. Adv. Opt. Mater. 3, 1374–1380 (2015).
Qu, S. et al. Controlling dispersion characteristics of terahertz metasurface. Sci. Rep. 5, 9367 (2015).
Zhang, X. et al. Broadband terahertz wave deflection based on C-shape complex metamaterials with phase discontinuities, Adv. Mater. 25, 4567–4572 (2013).
Pors A., Albrektsen, O., Radko, I. P. & Bozhevolnyi S. I. Gap plasmon-based metasurfaces for total control of reflected light, Sci. Rep. 3, 2155 (2013).
Cui, T. J., Qi, M. Q., Wan, X., Zhao J. & Cheng, Q. Coding metamaterials, digital metamaterials and programmable metamaterials, Light Sci. Appl. 3, e218 (2014).
Sun, S. et al. Gradient-index meta-surfaces as a bridge linking propagating waves and surface waves. Nature Mater. 11, 426–431 (2012).
Pu. M. et al. Broadband anomalous reflection based on gradient low-Q meta-surface. AIP Adv. 3, 052136 (2013).
Ma, H. F., Wang, G. Z., Kong, G. S. & Cui, T. J. Independent controls of differently-polarized reflected waves by anisotropic metasurfaces. Sci. Rep. 5, 9605 (2015).
Ma, H. F., Wang, G. Z., Kong, G. S. & Cui, T. J. Broadband circular and linear polarization conversions realized by thin birefringent reflective metausrfaces. Opt. Meter. Express 4, 1717–1724 (2014).
Xu, H. et al. Dynamical control on helicity of electromagnetic waves by tunable metasurfaces, Sci. Rep. 6, 27503 (2016).
Li, Y., Liang, B., Gu, Z., Zou, X. & Cheng, J. Reflected wavefront manipulation based on ultrathin planar acoustic metasurfaces. Sci. Rep. 3, 2546 (2013.
Tang, K. et al. Anomalous refraction of airborne sound through ultrathin metasurfaces, Sci. Rep. 4, 6517 (2014).
Xie, Y. et al. wavefront modulation and subwavelength diffractive acoustics with and acoustic metasurface, Nat. Commun. 5, 5553 (2014).
Ma, G., Yang, M., Xiao, S., Yang, Z. & Sheng, P. Acoustic metasurface with hybrid resonances, Nat. Mater. 13, 873–878 (2014).
M. Kraft, Y. Luo, S. A. Maier & J. B. Pendry Designing plasmonic grating with transformation optics. Phys. Rev. X. 5, 031029 (2015).
Chin, J. Y., Lu, M. & Cui, T. J. Metamaterial polarizers by electric-field-coupled resonators. Appl. Phys. Lett. 93, 251903 (2008).
Gansel, J. K. et al. Gold helix photonic metamaterial as broadband circular polarizer. Science 325, 1513–1515 (2009).
Grady, N. K. et al. Terahertz Metamaterials for Linear Polarization Conversion and Anomalous Refraction. Science 340, 1304–1307 (2013).
Zhao, Y., Belkin, M. A. & Alu, A. Twisted optical metamaterials for planarized ultrathin broadband circular polarizers, Nat. Commun. 3, 870 (2012).
Pu, M. et al. Anisotropic meta-mirror for achromatic electromagnetic polarization manipulation. Appl. Phys. Lett. 102, 131906 (2013).
Pfeiffer, C. & Grbic, A. Cascaded metasurfaces for complete phase and polarization control. Appl. Phys. Lett. 102, 231116 (2013).
Levesque, Q. et al. Plasmonic planar antenna for wideband and efficient linear polarization conversion. Appl. Phys. Lett. 104, 111105 (2014).
Wu, S. et al. Enhanced rotation of the polarization of a light Beam transmitted through a silver film with an array of perforated S-shaped holes. Phys. Rev. Lett. 110, 207401 (2013).
Sieber, P. E. & Werner, D. H. Reconfigurable broadband infrared circularly polarizing reflectors based on phase changing birefringent metasurfaces. Opt. Express 21, 1087–1110 (2013).
Yang, Y. et al. Dielectric meta-reflectarray for broadband linear polarization conversion and optical vortex generation. Nano Lett. 14, 1394–1399 (2014).
Gao, X. et al. Ultrawideband and high-efficiency linear polarization converter based on double V-shaped metasurface. IEEE Trans. Antennas Propag. 63, 3522–3530 (2015).
Wan, X. et al. Manipulations of Dual Beams with Dual Polarizations by Full-Tensor Metasurfaces, Adv. Opt. Mater. doi: 10.1002/adom.201600111 (2016).
Qi, M. Q. et al. A wideband waveguide antenna with nearly equal E- and H-plane radiation pattern. Int. J. Antennas Propag. 2013, 608393 (2013).
Nayeri, P., Yang, F. & Elsherbeni, A. Z. Design and experiment of a single-feed quad-beam reflectarray antenna. IEEE Trans. Antennas Propag. 60, 1166–1171 (2012).
Nayeri, P., Yang, F. & Elsherbeni, A. Z. Design of single-feed reflectarray antennas with asymmetric multiple beams using the particle swarm optimization method. IEEE Trans. Antennas Propag. 61, 4598–4605 (2013).
Acknowledgements
This work was supported in part from the National Natural Science Foundation of China under Grant Nos 61302018, 61401089, 61401091, 61571117, 61501112, 61501117 and 61138001, in part from the 111 Project under Grant No. 111-2-05, and in part from the the National Instrumentation Program under Grant No. 2013YQ200647, in part from the National Science Foundation of Jiangsu Province under No. BK20150020, in part by the Fundamental Research Funds for the Central Universities.
Author information
Authors and Affiliations
Contributions
H.F.M. designed, performed, interpreted the experiments and wrote manuscript. Y.Q.L. generated numerical simulations and interpreted the experiments. K.L. interpreted the experiments. T.J.C. supervised and interpreted the design and experiments.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Ma, H., Liu, Y., Luan, K. et al. Multi-beam reflections with flexible control of polarizations by using anisotropic metasurfaces. Sci Rep 6, 39390 (2016). https://doi.org/10.1038/srep39390
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep39390
This article is cited by
-
Phase gradient metasurface with broadband anomalous reflection based on cross-shaped units
Applied Physics A (2018)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.