Abstract
The standard approach to the analysis of genome-wide association studies (GWAS) is based on testing each position in the genome individually for statistical significance of its association with the phenotype under investigation. To improve the analysis of GWAS, we propose a combination of machine learning and statistical testing that takes correlation structures within the set of SNPs under investigation in a mathematically well-controlled manner into account. The novel two-step algorithm, COMBI, first trains a support vector machine to determine a subset of candidate SNPs and then performs hypothesis tests for these SNPs together with an adequate threshold correction. Applying COMBI to data from a WTCCC study (2007) and measuring performance as replication by independent GWAS published within the 2008–2015 period, we show that our method outperforms ordinary raw p-value thresholding as well as other state-of-the-art methods. COMBI presents higher power and precision than the examined alternatives while yielding fewer false (i.e. non-replicated) and more true (i.e. replicated) discoveries when its results are validated on later GWAS studies. More than 80% of the discoveries made by COMBI upon WTCCC data have been validated by independent studies. Implementations of the COMBI method are available as a part of the GWASpi toolbox 2.0.
Similar content being viewed by others
Introduction
The goal of genome-wide association studies (GWAS) (e.g. the WTCCC study1) is to examine the relationship between genetic markers such as single-nucleotide polymorphisms (SNPs) and individual traits, which are usually complex diseases or behavioral characteristics. Generally, a large number of statistical tests are performed in parallel, each SNP being individually tested for association2,3,4. The standard approach consists of computing individual, SNP-specific p-values corresponding to a statistical association test and comparing these p-values against some given significance threshold (say t*), meaning that precisely those SNPs with p-values smaller than t*are declared to be associated with the trait4,5,6. We refer to this approach as raw p-value thresholding (RPVT) and review some standard methods for choosing t*for the purpose of controlling multiple type I error rates (in particular, the family-wise error rate (FWER) and the expected number of false rejections (ENFR)) in the Methods Section.
According to the GWAS catalog7,8 (last accessed 03-07-2015), the more than 1,400 GWAS published so far have led to the identification of more than 11,000 SNPs associated with about 800 human diseases and anthropometric traits with p-values using t* = 1 × 10−5.
However, variants reported by GWAS tend to explain only small fractions of individual traits, and most of the heritability accounting for many complex diseases remains unexplained — a phenomenon usually referred to as the “mystery of missing heritability”4,9. There are several possible (not mutually exclusive) explanations for that phenomenon10,11,12,13. One frequently discussed possibility is that epistatic interactions between loci are ignored both in current heritability estimates and in usual testing procedures12,14. In addition to this issue, another shortcoming of current approaches based on testing each SNP independently is that they disregard any correlation structures among the set of SNPs under investigation that are introduced by both population genetics (linkage disequilibrium, LD) and biological relations (e.g. functional relationships between genes). The latter issue by itself is likely to introduce confounding factors and artifacts, implying a loss in statistical power15 and a lack of reliable insights about genotype-phenotype associations.
In this work, we propose a novel methodology — COMBI — that is a principled, reliable, and replicable method for identifying significant SNP-phenotype associations. The core idea is a two-step algorithm consisting of
-
1
a machine learning and SNP selection step that drastically reduces the number of candidate SNPs by selecting only a small subset of the most predictive SNPs; and
-
2
a statistical testing step where only the SNPs selected in step 1 are tested for association.
The main idea underlying COMBI is the use of the state-of-the-art machine learning technique support vector machine (SVM)16,17,18 in the first step. Crucially, this method is tailored to predict the target output (here, the phenotype) from high-dimensional data with a possibly complex, unknown correlation structure. In our application, the SVM is trained using the complete SNP data of one chromosome. Thus, the first step acts as a filter, indicating SNPs that are relevant for phenotype classification with either high individual effects or effects in combination with the rest of SNPs, while discarding artifacts due to the correlation structure. The second step uses multiple statistical hypotheses testing for a quantitative assessment of individual relevance of the filtered SNPs. All in all, the two steps extract complementary types of information, which are combined in the final output. Importantly, the calibration of the method is such that a global statistical error criterion is controlled for the entire procedure consisting of steps 1 and 2.
The following section first introduces the methodology in a summary paragraph and in Fig. 1; then, the Methods Section continues to explain the method in more detail with some references to Supplementary Section 1. An overview of related machine learning work is given in the Discussion Section. The performance of the COMBI method is reported in the Results Section, Supplementary Sections 2 and 3; where we also include and discuss the highly favorable comparisons with the algorithms that could potentially compete with the COMBI method. Note that COMBI yields better prediction with fewer false (i.e. non-replicated) and more true (i.e. replicated) discoveries when its results are validated on later, larger GWAS studies.
The COMBI method - Summary and illustration of the methodology.
Receiving genotypes and corresponding phenotypes of a GWAS as input, the COMBI method first applies a machine learning step to select a set of candidate SNPs and then calculates p-values and corresponding significance thresholds in a statistical testing step.
Implementations of the COMBI method are available in R, MATLAB, and JAVA, as a part of the GWASpi toolbox 2.0 (https://bitbucket.org/gwas_combi/gwaspi/).
Methods
Summary of The COMBI Method
Figure 1 shows a graphical representation of the COMBI method.
Input: a sample of observed genotypes {xi*} and corresponding phenotypes {yi}. We represent the j-th SNP of the i-th subject with a binary genotypic encoding, where xij = (1, 0, 0), xij = (0, 1, 0), or xij = (0, 0, 1), depending on the number of minor alleles. We assume a binary phenotype, i.e., yi ∈ {+1, −1}.
-
I
Machine learning and SNP-selection step (colored in red).
Based on the sample, an SVM is trained. The SVM returns a linear function f(x) = wTx, the sign of f(x) is a prediction of the unknown phenotype of a previously unseen genotype x. The absolute value |wj| of the corresponding component of the parameter vector w is interpreted for each SNP j as a measure of importance for the prediction function. The parameter vector w is then post-processed through a p-th-order moving average filter with window size l, that is,
 . Finally, the SNPs corresponding to the k largest values of the scores are selected; all other SNPs are discarded.
. Finally, the SNPs corresponding to the k largest values of the scores are selected; all other SNPs are discarded. -
II
Statistical testing step (colored in blue).
A hypothesis test (carried out as a χ2 test) is performed for each of the selected SNPs. Those SNPs with p-value less than a significance threshold t* are returned. The threshold t* is calibrated using a permutation-based method over the whole procedure consisting of the machine learning selection and statistical testing steps. See Algorithm 2 for details.
Problem Setting and Methodology
In this section, we formally describe the statistical problem under investigation and propose a novel methodology for tackling it — based on a combination of machine learning and statistical testing techniques.
Problem Setting and Notation
Let n denote the number of subjects in the study and d the number of SNPs under investigation. Given a sample of observed genotypes and corresponding phenotypes
and corresponding phenotypes , each xi* and each x*j corresponds to a subject and a SNP, respectively. A binary feature encoding is employed, where xij = (1, 0, 0), xij = (0, 1, 0), or xij = (0, 0, 1) depending on the number of minor alleles in SNP j of subject i. This paper focuses on binary phenotypes, i.e., yi ∈ {+1, −1} for all i = l, …, n. The data for one particular SNP can be summarized in a contingency table (See Table 1).
, each xi* and each x*j corresponds to a subject and a SNP, respectively. A binary feature encoding is employed, where xij = (1, 0, 0), xij = (0, 1, 0), or xij = (0, 0, 1) depending on the number of minor alleles in SNP j of subject i. This paper focuses on binary phenotypes, i.e., yi ∈ {+1, −1} for all i = l, …, n. The data for one particular SNP can be summarized in a contingency table (See Table 1).
The numbers nik denote the number of cases (i = 1) and controls (i = 2), respectively, which exhibit the genotype corresponding to column k. Notice that the row sums n1. and n2. are fixed and non-random by the experimental design (case-control study). Hence, the random vectors (n11, n12, n13)T and (n21, n22, n23)T follow a multinomial distribution with three categories, sample sizes n1. and n2., respectively; and unknown vectors of probabilities p1 = (p11, p12, p13)T and p2 = (p21, p22, p23)T, respectively. The parameter  of the statistical model for the whole study thus consists of all such pairs
of the statistical model for the whole study thus consists of all such pairs  of multinomial probability vectors, one for each of the d SNPs under investigation. For every SNP j, we are interested in testing the null hypothesis
of multinomial probability vectors, one for each of the d SNPs under investigation. For every SNP j, we are interested in testing the null hypothesis  , where we introduced the superscript j to indicate the SNP. This hypothesis is equivalent to the null hypothesis that the genotype at locus j is independent of the binary trait of interest. Two standard asymptotic tests for Hj versus its two-sided alternative Kj (genotype j is associated with the trait) are: the chi-square test for association and the Cochran-Armitage trend test (see, e.g., Sections 3.2.1 and 5.3.5 of the monograph by Agresti19). Both tests employ test statistics which are asymptotically (as min(n1., n2.) tends to infinity) chi-square distributed under Hj; the number of degrees of freedom equals 2 for the chi-square test for association, and 1 for the Cochran-Armitage trend test. Thus, p-values (pj: 1 ≤ j ≤ d) corresponding to these tests can be calculated by applying the upper-tail distribution function of the chi-square distribution with the corresponding degrees of freedom to the observed values of these statistics, and this for every SNP. Observe that the test statistics obtained for different SNPs will be highly correlated if these SNPs are in strong LD to each other; consequently, the corresponding p-values will also exhibit strong dependencies20,21.
, where we introduced the superscript j to indicate the SNP. This hypothesis is equivalent to the null hypothesis that the genotype at locus j is independent of the binary trait of interest. Two standard asymptotic tests for Hj versus its two-sided alternative Kj (genotype j is associated with the trait) are: the chi-square test for association and the Cochran-Armitage trend test (see, e.g., Sections 3.2.1 and 5.3.5 of the monograph by Agresti19). Both tests employ test statistics which are asymptotically (as min(n1., n2.) tends to infinity) chi-square distributed under Hj; the number of degrees of freedom equals 2 for the chi-square test for association, and 1 for the Cochran-Armitage trend test. Thus, p-values (pj: 1 ≤ j ≤ d) corresponding to these tests can be calculated by applying the upper-tail distribution function of the chi-square distribution with the corresponding degrees of freedom to the observed values of these statistics, and this for every SNP. Observe that the test statistics obtained for different SNPs will be highly correlated if these SNPs are in strong LD to each other; consequently, the corresponding p-values will also exhibit strong dependencies20,21.
RPVT declares a SNP j significantly associated with the trait if pj ≤ t*. If there was a single test to perform (i.e., d = 1), then t* would be taken as a pre-defined significance level α, as in the classical approach to statistical hypothesis testing. In multiple testing, however, the threshold t* is modified to take the multiplicity of the problem (the fact that d > 1) into account. The simplest method is the so-called Bonferroni correction,  . This choice guarantees that the FWER (that is, the probability of one or more erroneously reported associations) of the multiple test is bounded by α. A variety of other RPVT methods are explained, for instance, in the monograph by Dickhaus22.
. This choice guarantees that the FWER (that is, the probability of one or more erroneously reported associations) of the multiple test is bounded by α. A variety of other RPVT methods are explained, for instance, in the monograph by Dickhaus22.
Proposed workflow
The Bonferroni correction can only attain the prescribed FWER upper bound, and therefore have maximal power, if the p-values (pj:1 ≤ j ≤ d) do not exhibit strong (positive) dependencies, an assumption which is violated in GWAS due to strong LD in blocks of SNPs. An alternative way to calibrate the threshold t* for FWER control, taking the dependencies into account, is the Westfall-Young permutation procedure23, which controls the FWER under an assumption termed subset pivotality (see Westfall and Young23 as well as Dickhaus and Stange21). Furthermore, Meinshausen et al.24 proved that this permutation procedure is asymptotically optimal in the class of RPVT procedures, provided that the subset pivotality condition is fulfilled. However, for RPVT the individual p-value for association of the j-th SNP only depends on x*j and thus ignores the possible correlations with the rest of the genotype – which could yield additional information. By contrast, machine learning approaches aimed at prediction try to take the information of the whole genotype into account at once, and thus implicitly consider all possible correlations, to strive for an optimal prediction of the phenotype. Based on this observation, we propose Algorithm 1 combining the advantages of the two techniques, consisting of the following two steps:
-
the machine learning step, where an appropriate subset of candidate SNPs is selected, based on their relevance for prediction of the phenotype;
-
the statistical testing step, where a hypothesis test is performed together with a Westfall-Young type threshold calibration for each SNP.
Additionally, a filter first processes the weight vector w output in the machine learning step before using it for the selection of candidate SNPs. The above steps are discussed in more detail in the following sections.
The machine learning and SNP selection step
The goal in machine learning is to determine, based on the sample, a function f(x) that predicts the unknown phenotype y based on the observation of genotype x. It is crucial to require such a function to not only capture the sample at hand, but to also generalize, as well as possible, to new and unseen measurements, i.e., the sign of f(x) is a good predictor for y for previously unseen patterns x and labels y. We consider linear models of the form fw,b(xi*) = wTxi* + b in this paper. A popular approach to learning such a model is given by the SVM16,17,18, which determines the parameter w of the model by solving, for C > 0, the following optimization problem:

The problem above is similar to regression problems and can be interpreted as follows: we aim to minimize the trade-off (controlled by C) between a vector w with small norm (the term on the left-hand side) and small errors on the data (the term on the right-hand side). Once a classification function f has been determined by solving the above optimization problem, it can be used to predict the phenotype of any genotype by putting

The above equation shows that the largest components (in absolute value) of the vector w (called SVM parameter or weight vector) also have the most influence on the predicted phenotype. Note that the weights vector contains three values for each position due to the feature embedding, which encodes each SNP with three binary variables. To convert the vector back to the original length, we simply take the average over the three weights. We also include an offset by including a constant feature that is all one.
Considering that the use of SVM weights as importance measures is a standard approach25, for each j the score abs(wj) can be interpreted as a measure for the importance of the j-th SNP for the phenotype prediction task. The main idea is to select only a small number k of candidate SNPs before statistical testing, namely those SNPs having the largest scores. Based on preliminary experiments, we noticed that the introduction of the following additional post-processing of the SVM parameter vector was beneficial before SNP selection: a pth-order moving average filter is applied as follows:

where l ∈ 1, …, d denotes a fixed filter length (required to be an odd number). The value p ∈ ]0, ∞[is a free parameter; in the case p = 1, a standard moving average filter is obtained.
The statistical testing step
In the statistical testing step (see Summary of the COMBI method and Fig. 1), we apply p-value thresholding only to the k p-values which correspond to the SNPs with largest filtered SVM weights. Calculation of these p-values is performed exactly as described above for RPVT, with the only modification that p-values for SNPs not ranked among the top k in terms of their filtered SVM weights are set to 1, without calculating a test statistic.
The methodological challenge now consists of finding a threshold t*for the remaining k p-values such that the FWER is controlled for the multiple test which the entire workflow defines (SVM training, filtering of weights, p-value calculation, p-value thresholding). To this end, we investigated prior approaches26,27 based on sample splitting meaning that the selection of k SNPs is done on one (randomly chosen) sub-sample of individuals, while the p-value calculation and thresholding for the selected SNPs is performed on another. In this scheme, and regardless of which SNP selection method used on the first sub-sample, a Bonferroni-type threshold  guarantees FWER control at level α for the p-values computed on the second sub-sample. Since k ≪ d, this correction is much less conservative than the original Bonferroni correction using all SNPs. However, this is severely mitigated by the loss of power in the p-values due to the sample splitting. In fact, computer simulations (See Supplementary Section 2.2.4.) indicated very low power for detecting true associations with such a method because of the reduced sample size for calculation of test statistics and p-values.
guarantees FWER control at level α for the p-values computed on the second sub-sample. Since k ≪ d, this correction is much less conservative than the original Bonferroni correction using all SNPs. However, this is severely mitigated by the loss of power in the p-values due to the sample splitting. In fact, computer simulations (See Supplementary Section 2.2.4.) indicated very low power for detecting true associations with such a method because of the reduced sample size for calculation of test statistics and p-values.
Our suggestion is to re-sample the entire workflow of Fig. 1, thus following a Westfall and Young23 type procedure, and to choose t* based on the permutation distribution of the re-sampled p-values.
In summary, the proposed methodology is formally stated as Algorithm 1.

FWER control at level α of the multiple test defined by Algorithm 1 can be proven under a relaxed form of the subset pivotality condition, the validity of which is checked empirically in Supplementary Sections 2.2.1 and 2.2.2. To describe this condition formally, let  denote any probability measure under the global null hypothesis of no informative SNPs in {1, …, d} at all. We assume that the following condition holds true: Let p* denote the smallest of the k p-values corresponding to the positions picked by the SVM method for which the null hypothesis of no association between SNP and trait is true. Regarding p* as a random variable, assume that its distribution under the true data-generating distribution
denote any probability measure under the global null hypothesis of no informative SNPs in {1, …, d} at all. We assume that the following condition holds true: Let p* denote the smallest of the k p-values corresponding to the positions picked by the SVM method for which the null hypothesis of no association between SNP and trait is true. Regarding p* as a random variable, assume that its distribution under the true data-generating distribution  (which is unknown) is stochastically not smaller than under
(which is unknown) is stochastically not smaller than under  .
.
The distribution under  of the k p-values corresponding to positions chosen by applying the SVM method is now estimated by the resampling procedure given below as Algorithm 2. The algorithm repeatedly assigns a random permutation of the phenotypes yπ(1), …, yπ(n) to the observed genotypes x1*, …, xn*. The empirical lower α-quantile of the smallest of these k p-values is then a valid choice for t* in the sense that the FWER for the entire procedure defined by Algorithm 1 is bounded by α.
of the k p-values corresponding to positions chosen by applying the SVM method is now estimated by the resampling procedure given below as Algorithm 2. The algorithm repeatedly assigns a random permutation of the phenotypes yπ(1), …, yπ(n) to the observed genotypes x1*, …, xn*. The empirical lower α-quantile of the smallest of these k p-values is then a valid choice for t* in the sense that the FWER for the entire procedure defined by Algorithm 1 is bounded by α.

Note that the choice k = d leads to skipping the SVM step and arriving at the popular MinP procedure, originally proposed in Westfall and Young23. Following the argumentation in Dudoit and van der Laan28, it is also possible to control the generalized FWER (gFWER) with parameter l ≥ 1with the aforementioned resampling scheme as well as the ENFR. For gFWER control with parameter l, one has to consider the (l + 1)th-smallest of the re-sampled p-values, instead of  in Algorithm 2. For ENFR control, one has to store all B * k computed p-values and determine the p-value threshold that leads to an average number of rejections (over the B Monte Carlo repetitions) which matches the desired ENFR level. Moreover, so-called augmentation techniques28 can be utilized to control the false discovery rate (FDR) instead of the FWER.
in Algorithm 2. For ENFR control, one has to store all B * k computed p-values and determine the p-value threshold that leads to an average number of rejections (over the B Monte Carlo repetitions) which matches the desired ENFR level. Moreover, so-called augmentation techniques28 can be utilized to control the false discovery rate (FDR) instead of the FWER.
Results
Validation
Validation using simulated phenotypes
To assess the performance of the proposed COMBI method in comparison to other methods in a controlled environment, we conducted a number of simulation experiments with semi-real data. A block of 10,000 genotypes were taken from real WTCCC data1 without breaking linkage, but the phenotypes were synthetically generated according to a known model. This ensures that the “basic truth” is known (allowing us to compute the number of true and false positives for each method in the comparison). We show that COMBI outperforms the most commonly used methods for GWAS on these data sets. For instance, it achieves higher true positive rates for all family-wise error levels than any other method that we have investigated26,29,30, including RPVT. In comparison to RPVT, the gain in true positive rate is up to 80%. For a detailed description and analysis of the semi-real data simulations, see Supplementary Section 2.
Validation using WTCCC data
We then compared the performance of the COMBI method to that of other methods when applied to data from the 2007 WTCCC phase 1, consisting of 14,000 cases of seven common diseases and 3,000 shared controls (see Supplementary Section 3 for further information). In contrast to the simulations described above, the true underlying architecture of the traits under study is largely unknown. Hence, we used replicability in independent studies, one of the standards in the field, as a measure of performance. In summary, we proceeded as follows: the application of some method (for instance, COMBI or RPVT) to the 2007 WTCCC data results in a list of SNPs that are potentially associated with the trait (this is illustrated on the left-hand side of Fig. 2).
We then evaluated this list of potentially associated SNPs for replicability on independent data to obtain the “List of confirmed associated SNPs” (illustrated on the right-hand side of Fig. 2). All studies for the WTCCC diseases included in the GWAS catalog by June 26, 2015 constituted the set of studies examined for replicability. Most of these studies were performed either with larger sample sizes or using meta-analysis techniques and were published after the original WTCCC paper. In a sense, we thus examined how well any particular method, when applied to the WTCCC dataset, is able to make discoveries in that dataset that were actually confirmed by later research using RPVT in independent publications.
Our validation procedure considers a physical window of 200kb around a certain SNP and selects all SNPs with strong LD (R2 > 0.8) with the original SNP within that window. It queries the GWAS catalog for those SNPs to find out whether the selected SNPs have any entries. A hit indicates that a GWAS other than the original WTCCC study has since reported this SNP to be associated with the disease. Note that the GWAS catalog only contains SNPs with p-values < 10−5, meaning that we will miss some hits that are statistically weak but that might be biologically relevant, in the sense that they contribute to the classification of individuals according to phenotypes. For a detailed description of the automatic validation procedure, see Supplementary Section 3.2. With this procedure, methods can be compared by counting the respective number of replicated and non-replicated reported associations.
Regarding significance levels, we aimed to stay as close in line with the original WTCCC study as possible, reporting not only the strong associations at the significance level of 5 × 10−7 but also weak associations at 1 × 10−5. Within our validation pipeline we considered the full NHGRI GWAS Catalog7 with the inclusion criterion of having achieved a p-value of 1×10−5 in a GWAS. The “somewhat liberal statistical threshold of p < 1 × 10−5 was chosen to allow examination of borderline associations and to accommodate scans of various sizes while maintaining a consistent approach”7.
We also ensured that the same statistical criterion (control of the FWER or the ENFR, respectively) was used for all methods, in order to have a fair comparison. This procedure is explained in detail in the Methods Section and Supplementary Section 1.1.1.
Stability analysis
In addition, we established an “internal” validation by analyzing the stability of the reported associations (cf. Supplementary Section 3.4 for details); this stability measure indicates how well results can be reproduced on another independent sample.
Parameter selection
The analysis of WTCCC data required the selection of all free parameters of the COMBI method (e.g. the SVM optimization parameter C, the window size l of the moving average filter or the filter norm parameter p). To this end, the semi-real datasets investigated in Supplementary Section 2 have been used to determine performance changes induced by varying those free parameters. Since our findings were in agreement with related literature and mostly biologically sensible, the optimal settings were assumed to be good choices for the application of the COMBI method to real data. For example, it was found that aggregating SNPs within the filtering step (See Summary of the COMBI method and Fig. 1, the filtering step) based on a filter size of 35 is optimal, which is on the same magnitude as in Alexander and Lange31 who find that grouping of SNPs into bins of size 40 helps the performance of their algorithm. The moving average filter of the COMBI method is designed to correct for non-independence of statistical tests within LD blocks. Given the SNP density in the arrays used by the original WTCCC study and LD patterns in the CEU population (1000 Genomes), we estimate that the average LD block (r2 > 0.8) will harbor no more than 20–30 SNPs32, which supports our findings of setting the filter window size to 35 in the sense that we average-out blocks and conservatively add a bit of noise by potentially smoothing out signals across blocks.
See Supplementary Section 1.1 for a detailed description of the selection of all free parameters of the COMBI method.
Some parameters of the COMBI method could not be investigated within the simulation study, but had to be chosen manually for the WTCCC data. The decision to train the SVM separately on each chromosome was one of those tuning steps, as genome-wide training is very time and memory consuming on the one hand, and can only improve performance marginally on the other hand, as intergenic correlations between chromosomes are very rare.
Another parameter that was chosen manually was the number of active SNPs in one chromosome, i.e. the parameter k of The Screening Step presented in the Methods Section, which was set to 100 SNPs per chromosome after careful consideration. This choice is admittedly a wide, arbitrary upper bound for the number of SNPs that can present a detectable association with a given phenotype. Currently, the maximum total number of SNPs (not independent signals) associated with any phenotype is ~450 for human height and 180 for Crohn’s Disease (GWAS Catalog, accessed June 2015), so with k = 100 per chromosome one is well within what current evidence would support. After all, for future applications of COMBI k is a tuning parameter which has to be chosen by the researcher according to the assumed number of relevant loci.
The choice of exact values for all parameters will probably need to be adapted for each particular phenotype or disease under study, since they will have different genetic architectures and distribution of effect sizes4,9. For this manuscript and in order to provide a comprehensive and comparable set of results across many diseases we employed a unique set of parameter values supported by the results of our simulation study and other findings in related literature.
Manhattan plots and descriptive results
Figure 3 displays Manhattan plots for all seven diseases resulting from the standard RPVT approach (left) and the COMBI method (center) as well as the SVM weights (right). The center and right graph illustrates that the COMBI method discards SNPs with a low SVM score (cf. “The screening step” in Summary of the COMBI method and Fig. 1). Hence, the p-values for such SNPs are set to one without performing a statistical test, thereby drastically reducing the number of candidate associations. In contrast, the RPVT method results in p-values based on a formal significance test for every SNP, where many of these p-values are small and produce a lot of statistical noise. SNPs that show genome-wide statistical significance are highlighted in green in the left and right panel. For the standard RPVT, the threshold indicated by the horizontal dashed line is fixed a priori genome-wide. For the COMBI method, however, it was determined chromosome-wise via the permutation-based threshold over the whole COMBI procedure described in the Methods Section and Supplementary Section 1.1.1 to match the expected number of false rejections of RPVT.
Genome-wide scan for seven diseases.
Manhattan plots for all seven diseases resulting from the standard RPVT approach and the COMBI method as well as the SVM weights. We plot −log10 of the χ2 trend test p-values for both COMBI and RPVT and the corresponding SVM weights against position on each chromosome. Chromosomes are shown in alternating colours for clarity, with significant p-values highlighted in green. Please note that for the RPVT, the threshold indicated by the horizontal dashed line is fixed a priori genome-wide. For the COMBI method, it was determined chromosome-wise via the permutation-based threshold over the whole COMBI procedure. All panels are truncated at −log10 (p-value) = 15, although some markers exceed this significance threshold.
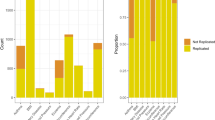
In Table 2, we present all significant associations reported by the COMBI method. Associations with a raw p-value > 10−5 were not reported in studies using only RPVT. If they are selected by the COMBI method, we consider them to be new findings and highlight them in grey. The last column of Table 2 indicates whether the reported associations were validated (i.e., were reported as significant in at least one independent study published after the WTCCC). The COMBI method finds 46 significant locations. 34 of these 46 significant locations have a p-value below 10−5 and were thus also found by the RPVT approach.
Crucially, our COMBI method found 12 additional SNPs. Out of these, ten (>83%) have already been replicated in later GWAS or meta analyses. The COMBI discoveries that have been replicated independently using individual SNP testing are for bipolar disorder rs2989476 (Chr. 1), rs1344484 (Chr. 16), rs4627791 (Chr. 3), and rs1375144 (Chr. 2); for coronary artery disease rs6907487 (Chr. 6) and rs383830 (Chr. 5); for Crohn’s disease rs12037606 (Chr. 1), rs10228407 (Chr. 7), and rs4263839 (Chr. 9) and for type 2 diabetes rs6718526 (Chr. 2). Given the current debate on the replicability of GWAS findings obtained by single-SNP analyses33, it is remarkable that GWAS studies published later had already replicated more than 83% of novel SNPs the COMBI method detected by reanalyzing data published in 2007.
Two out of the 12 SNPs with p-values exceeding 10−5 had not yet been reported in any GWAS or meta analyses as being associated with the corresponding diseases. Those are rs11110912 (Chr. 12) for hypertension and rs6950410 (Chr. 7) for type 1 diabetes. SNP rs11110912 was included in the original WTCCC analysis, but a p-value higher than 10−5 was obtained (1.94 × 10−5)1, so it was not collected in the GWAS Catalog. SNP rs6950410 has been detected as associated to multiple complex diseases34. Regarding the biological plausibility of these two SNPs, we examined a number of functional indicators to assess their potential role in disease. In particular, we explored the genomic regions in which they map and their potential roles as regulatory SNPs, status as eQTLs, and role in Mendelian disease. Overall, there is no strong evidence of functional roles (see Supplementary Section 3.5) but SNP rs11110912 (Chr. 12), for which COMBI suggested a link to hypertension, is an intronic SNP mapping on a gene, MYBPC1, that has been previously linked to familial hypertrophic cardiomyopathy, suggesting that COMBI has given rise to another interesting true positive finding.
GWAS catalog validation results – results obtained by the COMBI method are better replicated than those obtained by RPVT
The COMBI method also outperforms the RPVT approach for different type 1 error levels. Figure 4 shows the receiver operator characteristic (ROC) and precision-recall (PR) curves that have been generated based on the replication of SNPs according to the GWAS catalog (here, due to absence of basic truth knowledge, replicated reported associations are counted as true positives, and non-replicated associations as false positives). As the dark blue lines are consistently above the light blue lines, the COMBI method achieves both higher numbers of true positives (i.e. higher true positive rate (TPR)) as well as a higher precision (proportion of replicated associations amongst the SNPs classified as associated with the trait) for given numbers of false and true positives (i.e. lower false positive rate (FPR)) than RPVT for almost all levels of error. For comparison, we show also the result achieved when selecting SNP based on the highest SVM weights in absolute value (after filtering). The results show that discarding either one of the two steps in the COMBI method (machine learning or statistical testing step) will lead to a decrease in performance.
ROC and PR curves of the RPVT approach, the COMBI method and raw SVM weights using the independent validation pipeline as an indicator of replicability.
The results of all seven diseases have been pooled. The curves have been generated based on the replication of SNPs according to the GWAS catalog. Replicated reported associations are counted as true positives, and non-replicated associations as false positives. Note that the COMBI lines end at some point and the RPVT and the raw SVM lines continue. At the endpoint of the COMBI curve all SNPs selected in the SVM step are also significant in the statistical testing step; i.e. if one wanted to add just one more SNP to the list of reported associations, all other SNPs would also become significant, as they have a p-value of 1. The points on the RPVT and COMBI lines represent the final results of the two methods when applying the corresponding significance thresholds and are described in more detail in Table 3.
We now investigate the points on the curves that correspond to the application of t* = 10−5 in the case of RPVT and to the value of t* resulting from the permutation-based method in the case of the COMBI method (described in the Methods Section) in more detail. See Table 3 for the numbers corresponding to those points. A total of 78 SNPs were found to be significant with RPVT, since it only performs the statistical testing step, and 46 with the COMBI method, which has the additional layer of the machine learning screening step prior to the statistical testing.
Although the COMBI method finds fewer SNPs, the number of replicated SNPs is greater (28 in contrast to 24 of RPVT). The COMBI method also classifies only 18 of the unreplicated SNPs as associated with the trait (yielding a precision of 61%). This is in contrast to RPVT, which classifies 52 of the unreplicated SNPs as associated with the trait (yielding a precision of only 32%). In other words, if both methods are calibrated with respect to the same type I error criterion, the COMBI method reports significantly more replicated associations (Fisher’s exact test p-value of 0.0014).
Stability results – COMBI method is more stable than RPVT
From simulations considering internal stability, we found that the COMBI method produces more stable results than RPVT; cf. Supplementary Section 3.4 for details.
Runtime analysis and implementation details
The COMBI method is implemented in Matlab/Octave, R and Java as a part of the GWASpi toolbox 2.0 (https://bitbucket.org/gwas_combi/gwaspi/). The complete method is available in all these programming languages. The implementation for Matlab/Octave is cluster oriented and uses libLinear35. The Java implementation is desktop computer oriented and makes use of the following packages: libLinear35, libSVM36 and apache commons math37. Finally, the R implementation requires LiblineaR38, qqman39, data.table40, gtools41 and snpStats42.
The runtime of the method depends on a variety of factors such as available cluster memory, hardware resources and operating system. For this analysis we have run the method with the Matlab/Octave implementation on the following technical platform: 40 * Intel(R) Xeon(R) CPU E5-2650 v3 @ 2.30GHz 64bit, 128GB RAM, Ubuntu 14.04.4 LTS (GNU/Linux 3.13.0–79-generic x86_64), GNU Octave version 3.8.1. The analysis of WTCCC’s data on Crohn’s disease chromosome 18 (assuming calculations on more chromosomes can be computed in parallel if necessary) took 9h 15min and 24s. See Supplementary Section 3.7 for a more detailed runtime analysis.
Discussion
Several related machine learning methods have been successfully used in the context of statistical genomics. These approaches can be classified into two groups:
-
1
Methods that construct a model from genetic data in order to carry out accurate predictions on a phenotype43,44,45,46,47,48,49,50,51,52,53,54,55,56.
-
2
Methods that use machine learning to construct a statistical association test or rank genetic markers according to their predicted association with a phenotype30,31,57,58,59,60,61,62,63,64,65,66,67.
The set of papers that fall into the first category study the predictive performance of penalized regression and classification models including support vector machines16,17,18, random forests68, and sparsity-inducing methods such as the elastic net69 on various complex diseases (including the ones studied here), showing that machine learning methods such as SVMs – if appropriately applied - can perform well at predicting disease risks. See Supplementary Section 3.3, where we compare the prediction performance of various methods on the WTCCC data.
However, the main point of interest of the present contribution does not lie in risk prediction but rather in the identification of regions associated with diseases. The COMBI method should thus be compared to true alternative methods that stem from the second category, some of which include two-stage approaches first performing statistical testing and then machine learning to refine the set of predicted associations30,57. These approaches, however, are unable to identify correlation structures of SNPs that have been excluded in the first step and neither method is validated on real data in terms of a comparison to the GWAS database. Similarly, Pahikkala et al.59 and He and Lin60 develop methods for ranking genetic markers based on the sure independence screening strategy70 and stability selection analyzing only one SNP at a time. Recently the approach has been extended to detect gene-to-gene interactions by Li et al.71, but neither of the methods have been validated on independent external studies.
Another approach is by Alexander and Lange31, who apply the stability selection method of Meinshausen and Bühlmann58 to the WTCCC data set to rank SNPs according to their predicted association with a phenotype. The authors find that stability selection effectively controls the FWER when applied to GWAS data but suffers a loss of power, while at the same time rendering conservative results.
The work that is probably most closely related to the present research is the two-step algorithm by Wasserman and Roeder27 (and the extension by Meinshausen et al.26), who split the data into two equal parts performing marker selection on the first part and then testing the selected markers on the second part. See Supplementary Section 2.2.4 for a detailed description of this approach.
In order to investigate and compare performance of the COMBI method to other machine learning approaches, the work of Roshan et al.30, Wasserman and Roeder27 and Meinshausen et al.26 are selected as representative baseline methods. In Supplementary Section 2.2.4, we show that the COMBI approach outperforms all of these methods on semi-real data.
An important and very closely related recent method by Lippert et al.14,72 aims to identify putative significant disease-marker associations using two approaches based on linear mixed models (LMMs): a univariate test and a test for pairwise epistatic interactions. LMMs, like COMBI, address the issue of population stratification in GWAS, cf. Mimno et al.73. However, in contrast to COMBI, they still test SNPs (or pairs of SNPs) individually one after the other and thus potentially lose detection power. Another possible shortcoming of LMMs and related methods over SVMs is that they are more tailored for regression and not binary classification. For a comparison of COMBI with Lippert et al.14,72 on real WTCCC data see Supplementary Section 3.6. Recently their approach has been extended for disease risk prediction (Rakitsch et al.56) and related approaches have been proposed by Loh et al.74 and Song et al.75 suffering the same drawbacks as discussed above.
An extension of LMMs to multivariate cases was developed by Zhou and Stephens76, but has not yet been applied to WTCCC. Fitting LMMs to multiple phenotypes provides no novel insight into analyzing multiple genotypes/SNPs at once, which is the issue COMBI addresses.
Our approach can be extended to explore a number of different research directions by substituting one of the two steps of the algorithm with other suitable procedures. Thus, one could either apply other machine learning prediction methods (as mentioned above) instead of training an SVM in the first step of the COMBI method. For example, the SVM training could be replaced by a SNP selection by random forests or component-wise boosting. Alternatively, one could perform a different statistical test in the final step of the COMBI method, such as procedures correcting for population structures or other confounding factors72,77. These alternatives are possible options for future research (and some have been implemented in the literature), however, COMBI performs better than any of the other machine learning methods we compared it to (Supplementary Section 2.2.4).
COMBI also seems to perform better than other state-of-the-art methods for univariate analyses. For instance, a recent method by Lippert et al.14 aims to identify putative significant disease-marker associations from the WTCCC data using two approaches based on linear mixed models: an univariate test and a test for pairwise epistatic interactions. When their univariate method results are checked against the same validation criteria that we used for COMBI, it turns out that our method reports 17 more true positives (4.4 times more positives) for the three diseases for which their univariate method reports at least one hit (Supplementary Section 3.6).
The COMBI method also holds great potential for testing pairwise SNP-trait associations, as it drastically reduces the number of candidate associations by selecting a subset of the most predictive SNPs in the machine learning step. Again, a comparison against the method Lippert et al.14 propose for detecting epistatic interactions, is favorable to COMBI (see Supplementary Section 3.6). In future work we will extend the COMBI method to a regression setup where the phenotype is not binary.
To summarize, we proposed a novel and powerful method for analyzing GWAS data that is based on applying a carefully designed machine learning step that is tailored to the GWAS data before applying a classical multiple testing step. Certain machine learning models, in particular appropriately designed linear SVMs, take high-dimensional correlation structures into account and thus implicitly incorporate interactions between different loci. A subset of predictive candidate SNPs is extracted within the machine learning step. The p-values corresponding to association tests are then thresholded for these candidate SNPs in a subsequent statistical testing step. The COMBI method was shown to outperform the RPVT approach both on controlled, semi-real data and on data from the WTCCC 2007 study, for which reported associations were validated by their replicability in external later studies. The empirical analysis showed a significant increase in detection power for replicated SNPs, while yielding fewer unconfirmed discoveries. Two new (as yet unreplicated) candidate associations were reported.
Additional Information
How to cite this article: Mieth, B. et al. Combining Multiple Hypothesis Testing with Machine Learning Increases the Statistical Power of Genome-wide Association Studies. Sci. Rep. 6, 36671; doi: 10.1038/srep36671 (2016).
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
The Wellcome Trust Case Control Consortium. Genome-wide association study of 14,000 cases of seven common diseases and 3,000 shared controls. Nature 447, 661–678 (2007).
Wray, N. R. et al. Pitfalls of predicting complex traits from SNPs. Nat. Rev. Genet. 14, 507–515 (2013).
Edwards, S. L., Beesley, J., French, J. D. & Dunning, A. M. Beyond GWASs: illuminating the dark road from association to function. Am. J. Hum. Genet. 93, 779–797 (2013).
Visscher, P. M., Brown, M. A., McCarthy, M. I. & Yang, J. Five years of GWAS discovery. Am. J. Hum. Genet. 90, 7–24 (2012).
Ripke, S. et al. Genome-wide association analysis identifies 13 new risk loci for schizophrenia. Nat. Genet. 45, 1150–1159 (2013).
Beecham, A. H. et al. Analysis of immune-related loci identifies 48 new susceptibility variants for multiple sclerosis. Nat. Genet. 45, 1353–1360 (2013).
Hindorff, L. A. et al. Potential etiologic and functional implications of genome-wide association loci for human diseases and traits. Proc. Natl. Acad. Sci. 106, 9362–9367 Catalog of Published Genome-Wide Association Studies at www.genome.gov/gwastudies (2009).
Welter, D. et al. The NHGRI GWAS Catalog, a curated resource of SNP-trait associations. Nucleic Acids Res. 42, D1001–D1006 (2014).
Manolio, T. a. et al. Finding the missing heritability of complex diseases. Nature 461, 747–753 (2009).
Lee, S. H., Wray, N. R., Goddard, M. E. & Visscher, P. M. Estimating missing heritability for disease from genome-wide association studies. Am. J. Hum. Genet. 88, 294–305 (2011).
Gibson, G. Rare and common variants: twenty arguments. Nat. Rev. Genet. 13, 135–145 (2012).
Zuk, O., Hechter, E., Sunyaev, S. R. & Lander, E. S. The mystery of missing heritability: Genetic interactions create phantom heritability. Proc. Natl. Acad. Sci. 109, 1193–1198 (2012).
Mackay, T. F. C. Epistasis and quantitative traits: using model organisms to study gene-gene interactions. Nat. Rev. Genet. 15, 22–33 (2014).
Lippert, C. et al. An exhaustive epistatic SNP association analysis on expanded Wellcome Trust data. Sci. Rep. 3, 1099 (2013).
Van de Geer, S., Bühlmann, P., Ritov, Y. & Dezeure, R. On asymptotically optimal confidence regions and tests for high-dimensional models. Ann. Stat. 42, 1166–1202 (2014).
Boser, B. E., Guyon, I. M. & Vapnik, V. N. A Training Algorithm for Optimal Margin Classifiers. In Fifth Annual Workshop on Computational Learning Theory 144–152 (ACM Press, 1992).
Cortes, C. & Vapnik, V. Support-vector networks. Mach. Learn. 20, 273–297 (1995).
Müller, K. R., Mika, S., Rätsch, G., Tsuda, K. & Schölkopf, B. An introduction to kernel-based learning algorithms. IEEE Trans. neural networks 12, 181–201 (2001).
Agresti, A. Categorical Data Analysis. (Wiley, 2002).
Moskvina, V. & Schmidt, K. M. On multiple-testing correction in genome-wide association studies. Genet. Epidemiol. 32, 567–573 (2008).
Dickhaus, T. & Stange, J. Multiple point hypothesis test problems and effective numbers of tests for control of the family-wise error rate. Calcutta Stat. Assoc. Bull. 65, 123–144 (2013).
Dickhaus, T. Simultaneous Statistical Inference with Applications in the Life Sciences. (Springer, 2014).
Westfall, P. & Young, S. Resampling-Based Multiple Testing: Examples and Methods for p-Value Adjustment. (Wiley, 1993).
Meinshausen, N., Maathuis, M. H. & Bühlmann, P. Asymptotic optimality of the Westfall-Young permutation procedure for multiple testing under dependence. Ann. Stat. 39, 3369–3391 (2011).
Guyon, I. & Elisseeff, A. An introduction to variable and feature selection. Journal of machine learning research 3, 1157–1182 (2003).
Meinshausen, N., Meier, L. & Bühlmann, P. p-Values for High-Dimensional Regression. J. Am. Stat. Assoc. 104, 1671 (2009).
Wasserman, L. & Roeder, K. High-dimensional variable selection. Ann. Stat. 37, 2178–2201 (2009).
Dudoit, S. & van der Laan, M. Multiple Testing Procedures with Applications to Genomics. (Springer Science & Business Media, 2008).
Roeder, K. & Wasserman, L. Genome-Wide Significance Levels and Weighted Hypothesis Testing. Stat. Sci. 24, 398–413 (2009).
Roshan, U., Chikkagoudar, S., Wei, Z., Wang, K. & Hakonarson, H. Ranking causal variants and associated regions in genome-wide association studies by the support vector machine and random forest. Nucleic Acids Res. 39, e62 (2011).
Alexander, D. H. & Lange, K. Stability selection for genome-wide association. Genet. Epidemiol. 35, 722–728 (2011).
The HapMap International Consortium. A haplotype map of the human genome. Nature 437, 1299–1320 (2005).
Marigorta, U. M. & Navarro, A. High Trans-ethnic Replicability of GWAS Results Implies Common Causal Variants. PLoS Genet 9, e1003566 (2013).
Preuss, C., Riemenschneider, M., Wiedmann, D. & Stoll, M. Evolutionary dynamics of co-segregating gene clusters associated with complex diseases. PLoS One 7, e36205 (2012).
Fan, R.-E., Chang, K.-W., Hsieh, C.-J., Wang, X.-R. & Lin, C.-J. LIBLINEAR: A Library for Large Linear Classification. Journal of Machine Learning Research 9, 1871–1874. Software available at http://www.csie.ntu.edu.tw/~cjlin/liblinear (2008).
Chang, C.-C. & Lin, C.-L. LIBSVM: a library for support vector machines. ACM Trans. Intell. Syst. Technol. 2(27), 1–27. Software available at http://www.csie.ntu.edu.tw/~cjlin/libsvm (2011).
The Apache Software Foundation. Commons Math: The Apache Commons Mathematics Library. Java version 1.7. Software available at http://commons.apache.org/proper/commons-math/ (2016).
Helleputte, T. & Gramme, P. LiblineaR: Linear Predictive Models Based on the LIBLINEAR C/C++ Library. R package version 1.94-2 from http://dnalytics.com/liblinear/ (2015).
Turner, S. D. qqman: an R package for visualizing GWAS results using Q-Q and manhattan plots. biorXiv doi: 10.1101/005165. R package version 0.1.2 from http://cran.r-project.org/web/packages/qqman/ (2014).
Dowle, M., Srinivasan, A., Short, T. & Lianoglou, S. with contributions from Saporta, R. & Antonyan, E. data.table: Extension of Data.frame. R package version 1.9.6. from https://CRAN.R-project.org/package=data.table (2015).
Warnes, G. R., Bolker, B. & Lumley, T. gtools: Various R Programming Tools. R package version 3.5.0. from https://CRAN.R-project.org/package=gtools (2015).
Clayton, D. snpStats: SnpMatrix and XSnpMatrix classes and methods. R package version 1.22.0 from http://bioconductor.org/packages/release/bioc/html/snpStats.html (2015).
Mittag, F. et al. Use of support vector machines for disease risk prediction in genome-wide association studies: Concerns and opportunities. Hum. Mutat. 33, 1708–1718 (2012).
Davies, R. W. et al. Improved Prediction of Cardiovascular Disease Based on a Panel of Single Nucleotide Polymorphisms Identified Through Genome-Wide Association Studies. Circ. Cardiovasc. Genet. 3, 468–474 (2010).
Evans, D. M., Visscher, P. M. & Wray, N. R. Harnessing the information contained within genome-wide association studies to improve individual prediction of complex disease risk. Hum. Mol. Genet. 18, 3525–3531 (2009).
Ioannidis, J. P. A. Prediction of Cardiovascular Disease Outcomes and Established Cardiovascular Risk Factors by Genome-Wide Association Markers. Circ. Cardiovasc. Genet. 2, 7–15 (2009).
Kooperberg, C., LeBlanc, M. & Obenchain, V. Risk prediction using genome-wide association studies. Genet. Epidemiol. 34, 643–652 (2010).
Quevedo, J. R., Bahamonde, A., Perez-Enciso, M. & Luaces, O. Disease Liability Prediction from Large Scale Genotyping Data Using Classifiers with a Reject Option. IEEE/ACM Trans. Comput. Biol. Bioinforma. 9, 88–97 (2012).
Wei, Z. et al. From Disease Association to Risk Assessment: An Optimistic View from Genome-Wide Association Studies on Type 1 Diabetes. PLoS Genet. 5, e1000678 (2009).
Wei, Z. et al. Large Sample Size, Wide Variant Spectrum, and Advanced Machine-Learning Technique Boost Risk Prediction for Inflammatory Bowel Disease. Am. J. Hum. Genet. 92, 1008–1012 (2013).
Wray, N. R., Yang, J., Goddard, M. E. & Visscher, P. M. The genetic interpretation of area under the ROC curve in genomic profiling. PLoS Genet. 6, e1000864 (2010).
Austin, E., Pan, W. & Shen, X. Penalized regression and risk prediction in genome-wide association studies. Stat. Anal. Data Min. 6, 315–328 (2013).
Okser, S. et al. Regularized machine learning in the genetic prediction of complex traits. PLoS Genet. 10, e1004754 (2014).
Wu, Q., Ye, Y., Liu, Y. & Ng, M. K. SNP selection and classification of genome-wide SNP data using stratified sampling random forests. IEEE Trans. Nanobiosci. 11, 216–227 (2012).
Schwarz, D. F., König, I. R. & Ziegler, A. On safari to Random Jungle: a fast implementation of Random Forests for high-dimensional data. Bioinformatics 26, 1752–1758 (2010).
Rakitsch, B., Lippert, C., Stegle, O. & Borgwardt, K. A Lasso multi-marker mixed model for association mapping with population structure correction. Bioinformatics 29, 206–214 (2013).
Shi, G. et al. Mining gold dust under the genome wide significance level: a two-stage approach to analysis of GWAS. Genet. Epidemiol. 35, 111–118 (2011).
Meinshausen, N. & Bühlmann, P. Stability selection. J. R. Stat. Soc. Ser. B Statistical Methodol. 72, 417–473 (2010).
Pahikkala, T., Okser, S., Airola, A., Salakoski, T. & Aittokallio, T. Wrapper-based selection of genetic features in genome-wide association studies through fast matrix operations. Algorithms Mol. Biol. 7, 11 (2012).
He, Q. & Lin, D. Y. Y. A variable selection method for genome-wide association studies. Bioinformatics 27, 1–8 (2011).
Zhou, H., Sehl, M. E., Sinsheimer, J. S. & Lange, K. Association screening of common and rare genetic variants by penalized regression. Bioinformatics 26, 2375–2382 (2010).
Minnier, J., Yuan, M., Liu, J. S. & Cai, T. Risk classification with an adaptive naive Bayes Kernel machine model. J. Am. Stat. Assoc. 110, 393–404 (2015).
Nguyen, T. T., Huang, J. Z., Wu, Q., Nguyen, T. T. & Li, M. J. Genome-wide association data classification and SNPs selection using two-stage quality-based Random Forests. BMC Genomics 16, S5 (2015).
Tsai, M. Y. Variable selection in Bayesian generalized linear-mixed models: An illustration using candidate gene case-control association studies. Biometrical Journal 57, 234–253 (2015).
Manor, O. & Segal, E. Predicting disease risk using bootstrap ranking and classification algorithms. PLoS Comput. Biol. 9, e1003200 (2013).
Hoffman, G. E., Logsdon, B. A. & Mezey, J. G. PUMA: a unified framework for penalized multiple regression analysis of GWAS data. PLoS Comput. Biol. 9, e1003101 (2013).
Fisher, C. K. & Mehta, P. Bayesian feature selection for high-dimensional linear regression via the Ising approximation with applications to genomics. Bioinformatics 11, 1754–1761 (2015).
Breiman, L. Random forests. Machine learning 45, 5–32 (2001).
Zou, H. & Hastie, T. Regularization and variable selection via the elastic net. J. R. Stat. Soc. Ser. B Statistical Methodol. 67, 301–320 (2005).
Fan, J. & Lv, J. Sure independence screening for ultrahigh dimensional feature space. J. R. Stat. Soc. Ser. B Statistical Methodol. 70, 849–911 (2008).
Li, J., Zhong, W., Li, R. & Wu, R. A fast algorithm for detecting gene–gene interactions in genome-wide association studies. The annals of applied statistics 8, 2292 (2014).
Lippert, C. et al. FaST linear mixed models for genome-wide association studies. Nat. Methods 8, 833–835 (2011).
Mimno, D., Blei, D. M. & Engelhardt, B. E. Posterior predictive checks to quantify lack-of-fit in admixture models of latent population structure. Proc. Natl. Acad. Sci. 112, 3441–3450 (2015).
Loh, P. R. et al. Efficient Bayesian mixed-model analysis increases association power in large cohorts. Nat. Genet. 47, 284–290 (2015).
Song, M., Hao, W. & Storey, J. D. Testing for genetic associations in arbitrarily structured populations. Nat. Genet. 47, 550–554 (2015).
Zhou, X. & Stephens, M. Efficient multivariate linear mixed model algorithms for genome-wide association studies. Nat. Methods 11, 407–409 (2014).
Kang, H. M. et al. Efficient control of population structure in model organism association mapping. Genetics 178, 1709–1723 (2008).
Acknowledgements
This paper is part of a larger project on the genetics of social and economic behavior. The idea for this paper arose in the workshop that regularly takes place in the context of this project at the University of Zurich, and which is based on the collaboration of teams at universities in Berlin, Barcelona, Mainz, and Zurich. EF acknowledges support from the advanced ERC grant (ERC-2011-AdG 295642-FEP) on the Foundation of Economic Preferences. MK, BM, and KRM were supported by the German National Science Foundation (DFG) under the grants MU 987/6-1 and RA 1894/1-1. TD and DS were supported by the German National Science Foundation (DFG) under the grants DI 1723/3-1 und SCHU 2828/2-1. GB and TS acknowledge support of the German National Science Foundation (DFG) under the research group grant FOR 1735. MK, DT, KRM, and GB acknowledge financial support by the FP7-ICT Programme of the European Community, under the PASCAL2 Network of Excellence. MK acknowledges a postdoctoral fellowship by the German Research Foundation (DFG), award KL 2698/2-1, and from the Federal Ministry of Science and Education (BMBF) awards 031L0023A and 031B0187B. AN acknowledges support from the Spanish Multiple Sclerosis Network (REEM), of the Instituto de Salud Carlos III (RD12/0032/0011), the Spanish National Institute for Bioinformatics (PT13/0001/0026) the Spanish Government Grant BFU2012-38236 and from FEDER. This project has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No. 634143 (MedBioinformatics). MK and KRM were financially supported by the Ministry of Education, Science, and Technology, through the National Research Foundation of Korea under Grant R31-10008 (MK, KRM) and BK21 (KRM).
Author information
Authors and Affiliations
Contributions
E.F., T.D., G.B., D.S., A.N. and K.-R.M. designed and directed research; B.M., M.K., J.A.R., S.S., R.V., C M.-S., X.F., U.M.M. and D.S. performed research and analyzed data; and B.M., M.K., J.A.R., C M.-S., E.F., T.D., G.B., D.S., A.N. and K.-R.M. wrote the paper.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Mieth, B., Kloft, M., Rodríguez, J. et al. Combining Multiple Hypothesis Testing with Machine Learning Increases the Statistical Power of Genome-wide Association Studies. Sci Rep 6, 36671 (2016). https://doi.org/10.1038/srep36671
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep36671
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.



 . Finally, the SNPs corresponding to the k largest values of the scores are selected; all other SNPs are discarded.
. Finally, the SNPs corresponding to the k largest values of the scores are selected; all other SNPs are discarded.

