Abstract
Magnetic interactions in magnetic nanostructures are critical to nanomagnetic and spintronic explorations. Here we demonstrate an extremely sensitive magnetic yoking effect and tunable interactions in FePt based hard/soft bilayers mediated by the soft layer. Below the exchange length, a thin soft layer strongly exchange couples to the perpendicular moments of the hard layer; above the exchange length, just a few nanometers thicker, the soft layer moments turn in-plane and act to yoke the dipolar fields from the adjacent hard layer perpendicular domains. The evolution from exchange to dipolar-dominated interactions is experimentally captured by first-order reversal curves, the ΔM method, and polarized neutron reflectometry, and confirmed by micromagnetic simulations. These findings demonstrate an effective yoking approach to design and control magnetic interactions in wide varieties of magnetic nanostructures and devices.
Similar content being viewed by others
Introduction
Assessing and controlling interactions in magnetic nanostructures are critical to nanomagnetic and spintronic explorations, such as ultrahigh density magnetic recording1,2, exchange spring composites for permanent magnets3, artificially structured model systems of spin ice4,5,6 and analog memory7, and magnetic quantum-dot cellular automata8,9,10, etc. For example, in the emerging heat-assisted magnetic recording (HAMR) technology that separates the recording process at elevated temperatures from the ambient temperature storage environment11,12, a critical issue is to tailor the various magnetic interactions in the media13,14,15. These interactions are often complicated and correlated, e.g., exchange interaction within each grain vs. dipolar interactions across neighboring grains, which directly impact the media performance such as the thermal stability and switching field distribution. Careful balance of these interactions, e.g., through the introduction of boron or oxides at grain boundaries16,17, has been essential to optimizing the media performance. Another example is the exchange coupled media that uses a magnetically hard layer to anchor the thermal stability, while writeablity is achieved by exchange coupling to a neighboring magnetically soft layer18,19,20. The same concept has also been used to achieve high energy density permanent magnets, through enhancement of the maximum energy product3. Careful balancing of exchange and dipolar interactions are again important, as the physical dimensions of the magnetically hard/soft components need to be on the order of exchange length, to achieve these desirable effects.
In this work we demonstrate an extremely sensitive magnetic yoking effect and continuous tuning of interactions in a model system consisting of a magnetically hard L10-FePt layer with perpendicular magnetic anisotropy (PMA), a prototype HAMR media, and a magnetically soft layer with a varying thickness. The latter is shown to effectively moderate interactions between adjacent domains in the hard layer. By tailoring the soft layer thickness by just a few nanometers, across the exchange length, the dominant interaction in the bilayer system can be continuously tuned from exchange to dipolar. A yoking effect emerges as the soft layer magnetization turns in-plane to facilitate the dipolar interaction across neighboring L10-FePt domains with perpendicular magnetization, captured by magnetometry, polarized neutron reflectometry (PNR), magnetic imaging, and confirmed by micromagnetic simulations. These results demonstrate an effective yoking approach to tailor interactions in nanomagnetic building blocks for wide varieties of technological applications.
Results
Magnetometry
Thin film bilayers of L10-Fe52Pt48 (4 nm)/A1-Fe52Pt48 (tA1) with tA1 = 0 nm–9 nm were fabricated by sputtering, as described in Methods. Magnetometry measurements were performed at room temperature in the out-of-plane geometry, unless otherwise noted. Hysteresis loops for the films are shown in Fig. 1. For the 4 nm L10-FePt film alone (tA1 = 0 nm), a square hysteresis loop is observed with a coercivity of 320 mT in the perpendicular geometry (panel a), while the in-plane loop is closed (panel b), indicating a clear perpendicular anisotropy expected of (001) oriented L10-FePt. For films with increasing tA1, in the perpendicular geometry the coercivity decreases and the loop develops a strong canting; magnetic moments associated with the slope are due to the in-plane soft layer, which is being reversibly forced out-of-plane by the field. Note that for the sample with tA1 = 2 nm, the hysteresis loops are very similar to those for the L10-FePt alone, suggesting that the A1 layer orientation is dominated by the L10 layer through exchange coupling; this is consistent with the A1-layer’s exchange length of lex = 3.9 nm21. Once tA1 exceeds lex, significant in-plane magnetization is observed for tA1 = 5 nm and even more so for tA1 = 9 nm (Fig. 1), indicating more and more of the moments in the A1 layer are now in the film plane. The development of this in-plane reversal indicates that the A1 layer is able to switch with only limited dependence on the perpendicular L10 layer.
Magnetometry.
Major hysteresis loops of L10-FePt (4 nm)/A1-FePt (tA1) bilayer films in the (a) perpendicular and (b) in-plane orientation, normalized to the saturation magnetic moment of the L10-FePt. Samples are identified by color and symbol for tA1 = 0 nm (black squares), 2 nm (red circles), 5 nm (blue triangles) and 9 nm (green inverted triangles).
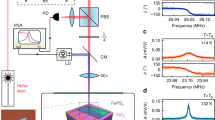
Polarized neutron reflectometry
The interfacial coupling was directly observed using specular PNR which is only sensitive to in-plane moments. Model fitted reflectometry data for tA1 = 2 nm and 5 nm bilayers, measured in a 50 mT field applied perpendicular to the film, after sequential saturation in the out-of-plane and then in-plane directions, are shown in Fig. 2a,b, respectively. The sample with a tA1 = 2 nm, panel a, shows no appreciable signal in the spin-flip channel (R+− and R−+), indicating negligible in-plane magnetization. In contrast, the tA1 = 5 nm sample, panel b, exhibits spin-flip scattering with intensity of the same order of magnitude as the non-spin-flip, identifying a significant in-plane magnetization. This is further confirmed in the fitted models (Fig. 2c,d), which show in-plane magnetization (ρM) only in the 5 nm sample. These PNR results are consistent with the magnetometry measurements shown in Fig. 1: when tA1 < lex, the magnetocrystalline anisotropy in the L10-FePt forces the moments in both layers to be out-of-plane; however, this effect is largely suppressed once tA1 > lex, resulting in significant in-plane magnetization. The non-spin-flip scattering depends only on the depth-dependent nuclear composition, and is consistent with the expected layer structure.
Polarized neutron reflectometry.
Polarized neutron reflectivity of L10-FePt(4 nm)/A1-FePt(tA1) with (a) tA1 = 2 nm and (b) tA1 = 5 nm, where the non-spin-flip channels are identified as black solid squares (R++) and blue solid circles (R−−) and spin-flip ones as red open triangles (R+−) and green open inverted triangles (R−+). Schematic insets show the spin configurations in the L10 layer (red) and A1 layer (purple), respectively. The corresponding nuclear and magnetic scattering length density (SLD) depth profiles for the samples with tA1 of 2 nm and 5 nm are shown in panels (c) and (d), respectively, which are also used to calculate the reflectivity shown in (a,b) as solid lines. The nuclear depth profile is shown as a black line, and the magnetic profile as a red line; background colors from left to right identify the SiO2 (grey), L10-FePt (coral), A1-FePt (light purple), Ti Cap (green), and air (white).
First-order reversal curves and ΔM method
Details of the magnetization reversal in L10-FePt (4 nm) /A1-FePt(tA1) were identified using the first-order reversal curve (FORC) technique22,23,24,25,26,27,28, as shown in Fig. 3. The FORC diagrams all show two key features: (1) a horizontal ridge, parallel to the H axis, and (2) a vertical ridge, essentially parallel to the HR axis. These type of features are commonly seen in PMA films which reverse by a domain nucleation/growth mechanism23,29,30. For the L10-FePt film alone, the horizontal FORC ridge is aligned to the left of the vertical ridge (as in a flipped L-shape), Fig. 3a, noted as “left bending” hereafter. As tA1 increases to 2 nm, Fig. 3b, the FORC features remain qualitatively the same, but shift to more positive values of HR and more negative values of H. With further increase in tA1 (now > lex), the horizontal feature moves to the right of the vertical one, noted as “right-bending” hereafter (Fig. 3c,d). While both left- and right-bending features have been observed in the literature23,29,30,31,32,33,34, there has been no distinction between them nor discussion of the origin of their left/right facing orientation.
FORC distribution and ΔM measurements.
(a–d) FORC distributions and (e) ΔM results of L10-FePt (4 nm)/A1-FePt(tA1) films where tA1 is (a) 0 nm, (b) 2 nm, (c) 5 nm and (d) 9 nm. Positive peaks of ΔM are characteristic of magnetizing (e.g. exchange) interactions, while negative ones indicate demagnetizing (e.g. dipolar) interactions. In panel (e) samples are identified by color and symbol for tA1 = 0 nm (black squares), 2 nm (red circles), 5 nm (blue triangles), and 9 nm (green inverted triangles).
We suggest that the orientation of the FORC features indicates the nature of the interactions, particularly between the L10 domains; the reversible behavior of the in-plane A1 layer measured in the out-of-plane direction, identified in Fig. 1a by the high field canting, are manifested in the FORC distribution as a reversible feature at H = HR (not shown). To qualitatively identify the interactions in the L10-FePt (4 nm)/A1-FePt(tA1) films we employ the ΔM technique (see Methods)35,36,37. At tA1 = 0 nm and 2 nm, whose FORC distributions show the left-bending characteristics, the ΔM plot shows a prominent positive feature, indicating primarily an exchange dominated interaction (Fig. 3e). At tA1 = 5 nm and 9 nm, whose FORC features are right-bending, the ΔM plot exhibits a negative feature (Fig. 3e), confirming a change in the dominant interaction from exchange to dipolar.
Magnetic force microscopy
The relative balance between exchange and dipolar interactions in these films can also be seen directly in the remanent domain structures captured by magnetic force microscopy (MFM) after perpendicular ac demagnetization, as shown in Fig. 4. At tA1 = 0 nm, the domain structure of L10-FePt film consists of large labyrinth domains (average size 8 × 104 nm2, Fig. 4a). With increasing tA1, the average domain size is shown to decrease (7 × 104 nm2, 3 × 104 nm2, 2 × 104 nm2 average for tA1 = 2 nm, 5 nm, and 9 nm, shown in Fig. 4b–d, respectively). In a simplistic consideration, for a PMA film, domain size is an indicator of the balance between the lateral exchange coupling and the dipolar interaction38. Generally, the domain wall energy per unit area increases with decreasing domain size, thus a strong exchange interaction favors fewer domain walls and larger domains; the demagnetization energy decreases with decreasing domain size, therefore a strong dipolar interaction favors smaller domains. In the present case, the magnetically hard L10-FePt film remains the same in all samples; as the soft A1 layer gets thicker, the rapid decrease in domain size suggests a relative increase of dipolar interactions, over exchange interactions, in the bilayer film.
Discussion
The ΔM measurements and MFM results suggest that the left- and right-bending FORC features are correlated with an exchange and dipolar-dominated interaction, respectively. Following directly from Davies et al.23,29, along decreasing reversal field HR, the horizontal FORC ridge in Fig. 3a–d marks the nucleation of reversal domains in the early stage of the magnetization reversal from positive saturation, and the vertical ridge (the range of HR) marks the later stage of annihilation of residual domains towards negative saturation. The applied field H-position of the vertical ridge also marks the nucleation field of reversal domains from those negative reversal fields, towards positive saturation. Indeed, with increased A1 layer thickness this nucleation field occurs sooner (vertical feature moves to -H). This is consistent with increased dipolar interactions, which will promote early reversal domain nucleation. Similar results are also found in the L10-FePt/Fe samples (see Supplementary Figs S1,S2 and S3). For samples with tA1 < lex, the A1 layer is strongly exchange coupled to the L10 layer, characteristic of exchange spring magnets18,39, with the magnetic moments aligned out-of-plane and the hard layer coercivity reduced. In the FORC distribution the coercivity reduction is manifested by the translation of the FORC feature to more positive values of HR and more negative values of H. When tA1 > lex, the major hysteresis loop and PNR results indicate an in-plane magnetic easy axis for the soft A1 layer. In the perpendicular L10 layer, neighboring domains will have exactly anti-parallel alignment due to its uniaxial anisotropy (as shown in Fig. 4), thus leading to strong dipolar fields. The in-plane component of the dipolar field is estimated to be much larger than the soft layer coercivity (see Supplementary Information). Thus, the A1 layer will have in-plane magnetizations which follow the dipolar fields from the L10 layer and form magnetic yokes to channel the flux40. The resultant dipolar interaction between adjacent domains in the L10 layer will be enhanced by the additional moments in the yoke, as observed in the FORCs, ΔM and MFM measurements.
The results from our micromagnetic simulations underpin the yoking mechanism inferred from the experimental data. As long as tA1 < lex (e.g., 2 nm in Fig. 5a), yoking is practically absent; magnetization in the soft phase is strongly exchange coupled to that in the hard phase, which results in a narrow Néel-type domain wall (nearly 180 degrees) with only a minor change in domain-wall width when going from the hard to the soft layer. The out-of-plane and in-plane component of the wall magnetization closely follow the theoretical curve given by  and
and  , respectively (dashed curves). For a tA1 ≈ 2lex (Fig. 5b), the domain wall in the upper part of the soft phase widens considerably and has a smaller amplitude variations due to the now predominant in-plane magnetization component in the soft layer. From the energy diagram (Fig. 5c), it can be seen that the demagnetizing energy for tA1 = 9 nm is greatly reduced compared to tA1 = 2 nm. This gain is a direct consequence of flux closure due to yoking and more than offsets the cost in exchange energy needed to deflect the soft-layer magnetization in-plane. For the case that the soft-layer domain is orthogonal to the hard-layer domain wall, shown in Fig. 5d for the modeled strip (1000 nm long, 10 nm wide) and Fig. 5e for the large block, the soft layer follows the dipolar fields forming a yoke structure, as described above. Figure 5d also demonstrates a multi-domain reversal in the thick A1 layer which is not commensurate with the domain structure in the L10 underlayer. Interestingly, despite their incommensurate domain structures, for the case that the soft-layer domain is oriented parallel to the domain wall, Fig. 5f, the yoking effect is still present and re-orients the soft-layer near the hard-layer domain wall to follow the dipolar fields. Thus, independent of the domain structure in the soft-layer, yoking is expected to occur and facilitates the dipolar interactions.
, respectively (dashed curves). For a tA1 ≈ 2lex (Fig. 5b), the domain wall in the upper part of the soft phase widens considerably and has a smaller amplitude variations due to the now predominant in-plane magnetization component in the soft layer. From the energy diagram (Fig. 5c), it can be seen that the demagnetizing energy for tA1 = 9 nm is greatly reduced compared to tA1 = 2 nm. This gain is a direct consequence of flux closure due to yoking and more than offsets the cost in exchange energy needed to deflect the soft-layer magnetization in-plane. For the case that the soft-layer domain is orthogonal to the hard-layer domain wall, shown in Fig. 5d for the modeled strip (1000 nm long, 10 nm wide) and Fig. 5e for the large block, the soft layer follows the dipolar fields forming a yoke structure, as described above. Figure 5d also demonstrates a multi-domain reversal in the thick A1 layer which is not commensurate with the domain structure in the L10 underlayer. Interestingly, despite their incommensurate domain structures, for the case that the soft-layer domain is oriented parallel to the domain wall, Fig. 5f, the yoking effect is still present and re-orients the soft-layer near the hard-layer domain wall to follow the dipolar fields. Thus, independent of the domain structure in the soft-layer, yoking is expected to occur and facilitates the dipolar interactions.
Micromagnetic simulations.
(a) Cross-section through a domain-wall at remanence after in-plane saturation for a block with dimensions x = 100 nm, y = 100 nm, z = (tL10 + tA1), where tL10 = 4 nm and tA1 = 2 nm. Top and bottom panels show out-of-plane and in-plane magnetization, respectively, across a domain wall for selected layers (z = 1 nm and 4 nm, i.e., base and top of the L10-FePt, and 5 nm and 6 nm, i.e., base and top of the A1- FePt). Dashed curves show theoretical magnetization curves, vertical dashed lines represent the theoretical domain-wall width  . (b) as in (a), but now for tA1 = 9 nm. (c) Contributions to free energy density F (top panel) along the magnetization curve shown in the bottom panel. All energy terms are normalized to the stray field energy constant. (d) Side-view example magnetization configuration in a long narrow strip (x = 1000 nm, y = 10 nm, z = (tL10 + tA1), with tL10 = 4 nm and tA1 = 5 nm) hosting domain walls in both the L10 and A1 layer, under in-plane field (µ0Hx = −0.1 T). Color coding indicates x-component of the magnetization. (e,f) Example magnetic configuration from large model (x = 1500 nm, y = 1500 nm, z = 10 nm) after domain nucleation, with color contrast in (e) indicating the out-of-plane magnetization, and in (f) indicating the into-the-page magnetization.
. (b) as in (a), but now for tA1 = 9 nm. (c) Contributions to free energy density F (top panel) along the magnetization curve shown in the bottom panel. All energy terms are normalized to the stray field energy constant. (d) Side-view example magnetization configuration in a long narrow strip (x = 1000 nm, y = 10 nm, z = (tL10 + tA1), with tL10 = 4 nm and tA1 = 5 nm) hosting domain walls in both the L10 and A1 layer, under in-plane field (µ0Hx = −0.1 T). Color coding indicates x-component of the magnetization. (e,f) Example magnetic configuration from large model (x = 1500 nm, y = 1500 nm, z = 10 nm) after domain nucleation, with color contrast in (e) indicating the out-of-plane magnetization, and in (f) indicating the into-the-page magnetization.
In summary, a magnetic yoking effect is observed in L10-FePt based hard/soft bilayers with perpendicular magnetization. The soft layer is shown to play a critical role in continuously tuning interactions between perpendicular magnetic moments in adjacent hard layer domains. When the soft layer is thinner than the exchange length, its moments strongly exchange couple to the L10-FePt and remain perpendicular to the film; as the soft layer becomes thicker than the exchange length, its moments turn in-plane and act to yoke the dipolar fields between neighboring hard-layer domains. This extreme sensitivity to the soft layer thickness, over a few nanometers, and the corresponding transition from exchange to dipolar dominated interactions are captured by ΔM measurements, as well as PNR and domain size analysis, and confirmed by micromagnetic modeling. These results suggest orientation of the boomerang FORC distribution may identify the dominant magnetic interactions. The yoking approach presents an effective mechanism to tailor magnetic interactions in elemental nanomagnetic building blocks, which have far-reaching potentials in numerous technological applications such as magnetic recording media, permanent magnets, magnetic memory and logic devices, etc.
Methods
Synthesis
Thin films of Fe52Pt48 (4 nm) were grown by dc magnetron co-sputtering from elemental targets on Si substrates with SiO2 (200 nm)/FeOx (<1 monolayer) buffer layers in a high-vacuum chamber (PBase < 1 × 10−4 Pa, PAr = 3 × 10−1 Pa). After deposition of the FePt, the film was exposed to a short oxygen plasma treatment (4:1 Ar:O2), realizing a thin oxide capping layer. The films were subsequently heated by rapid thermal annealing to 500 °C for 5 min in vacuum, following prior procedures41,42,43. X-ray diffraction indicates that the resultant films are L10 ordered with an (001) texture (not shown), similar to previous studies42. Thus this magnetically hard L10-FePt has its easy axis perpendicular to the film. Next, an A1-Fe52Pt48 film (with thickness tA1 = 0 nm–9 nm) and a 2 nm Ti capping layer were dc magnetron sputtered, which is magnetically soft with an easy axis in the film plane. The bilayer structure thus forms an exchange spring system18,19,20. Additional bilayer films with an Fe soft layer, rather than an A1-FePt, were also fabricated, as discussed in the Supplementary Information.
Characterizations
Magnetic properties were measured by a vibrating sample magnetometer (VSM) at room temperature with the applied field perpendicular to the film, unless otherwise stated. Details of the magnetization reversal were investigated using the FORC technique, which can identify different reversal mechanisms and distinguish interactions22,23,24,25,27,28. Starting at positive saturation the applied field, H, is reduced to a reversal field, HR. The magnetization, M, is measured as H is increased from HR to positive saturation. This is performed for a series of HR, collecting a family of FORCs. A mixed second order derivative extracts the normalized FORC distribution,  . The dominant magnetic interaction was also probed with ΔM measurements35,36,37:
. The dominant magnetic interaction was also probed with ΔM measurements35,36,37:  , where MDCD(H), MIRM(H) and MR are the dc demagnetization remanence, isothermal remanence, and saturation remanence, respectively. The value of ΔM is typically positive for magnetizing (exchange) interactions, and negative for demagnetizing (dipolar) interactions17,35,37. Atomic and magnetic force microscopy (AFM/MFM) were performed using a low-moment CoCr coated Si cantilever, in phase-detection mode.
, where MDCD(H), MIRM(H) and MR are the dc demagnetization remanence, isothermal remanence, and saturation remanence, respectively. The value of ΔM is typically positive for magnetizing (exchange) interactions, and negative for demagnetizing (dipolar) interactions17,35,37. Atomic and magnetic force microscopy (AFM/MFM) were performed using a low-moment CoCr coated Si cantilever, in phase-detection mode.
Polarized neutron reflectometry was performed at the NIST Center for Neutron Research on the polarized beam reflectometer (PBR) using 4.75 Å wavelength neutrons44,45. Measurements were performed with an out-of-plane guide field. In this geometry, the non-spin-flip scattering is sensitive to the depth profile of the nuclear scattering length density (ρN, indicative of the nuclear composition), while the spin-flip scattering is sensitive to the depth profile of the magnetic scattering length density (ρM, proportional to the magnetization)46. Modeling of the data was performed using the Refl1D software package47. Parallel fitting of datasets with coupled parameters was performed to promote uniqueness of the fit.
Micromagnetic simulations
Three dimensional micromagnetic simulations were performed using the object oriented micromagnetic framework (OOMMF) platform21. For a vertical construction of L10-FePt(tL10)/A1-FePt(tA1) with tL10 = 4 nm and variable tA1 (1 nm, 5 nm, and 9 nm), we simulated blocks with 100 nm × 100 nm × (tL10 + tA1) and 1000 nm × 10 nm × (tL10 + tA1), using a 1 nm cubic mesh, and a larger block of 1500 nm × 15 nm × 10 nm, using a 6 nm × 6 nm × 1 nm rectangular mesh21. The L10-FePt layer was modeled with saturation magnetization MS = 1150 emu·cm−3 (1 emu = 10−3 A·m2), anisotropy KU = 3.6 J·cm−3, exchange constant A = 1.3 × 10−13 J·cm−1 and the polycrystalline A1-FePt layer as MS = 1150 emu·cm−3, KU = 0, A = 1.3 × 10−13 J·cm−1 Ref. (48).
Additional Information
How to cite this article: Gilbert, D. A. et al. Magnetic Yoking and Tunable Interactions in FePt-Based Hard/Soft Bilayers. Sci. Rep. 6, 32842; doi: 10.1038/srep32842 (2016).
References
Skumryev, V. et al. Beating the superparamagnetic limit with exchange bias. Nature 423, 850–853 (2003).
Mangin, S. et al. Engineered materials for all-optical helicity-dependent magnetic switching. Nat Mater 13, 286–292 (2014).
Zeng, H., Li, J., Liu, J. P., Wang, Z. L. & Sun, S. H. Exchange-coupled nanocomposite magnets by nanoparticle self-assembly. Nature 420, 395–398 (2002).
Wang, R. F. et al. Artificial “spin ice” in a geometrically frustrated lattice of nanoscale ferromagnetic islands. Nature 439, 303–306 (2006).
Zhang, S. et al. Perpendicular magnetization and generic realization of the ising model in artificial spin ice. Phys. Rev. Lett. 109, 087201 (2012).
Gliga, S., Kákay, A., Hertel, R. & Heinonen, O. G. Spectral analysis of topological defects in an artificial spin-ice lattice. Phys. Rev. Lett. 110, 117205 (2013).
Kou, X. et al. Memory effect in magnetic nanowire arrays. Adv. Mater. 23, 1393 (2011).
Cowburn, R. P. & Welland, M. E. Room temperature magnetic quantum cellular automata. Science 287, 1466–1468 (2000).
Imre, A. et al. Majority logic gate for magnetic quantum-dot cellular automata. Science 311, 205–208 (2006).
Vedmedenko, E. Y., Mikuszeit, N., Oepen, H. P. & Wiesendanger, R. Multipolar ordering and magnetization reversal in two-dimensional nanomagnet arrays. Phys. Rev. Lett. 95, 207202 (2005).
Wu, A. Q. et al. HAMR areal density demonstration of 1+ tbpsi on spinstand. IEEE Trans. Magn. 49, 779–782 (2013).
Wang, X. B. et al. HAMR recording limitations and extendibility. IEEE Trans. Magn. 49, 686–692 (2013).
Weller, D., Mosendz, O., Parker, G., Pisana, S. & Santos, T. S. L10 FePtX–Y media for heat-assisted magnetic recording. Phys. Status Solidi A 210, 1245–1260 (2013).
Richter, H. J. et al. Recording potential of bit-patterned media. Appl. Phys. Lett. 88, 222512 (2006).
Valcu, B. F., Gilbert, D. A. & Liu, K. Fingerprinting Inhomogeneities in Recording Media using the First Order Reversal Curve Method. IEEE Trans. Magn. 47, 2988 (2011).
Weller, D. & Moser, A. Thermal effect limits in ultrahigh-density magnetic recording. IEEE Trans. Magn. 35, 4423–4439 (1999).
Liao, J. W. et al. Simultaneous enhancement of anisotropy and grain isolation in CoPtCr-SiO2 perpendicular recording media by a MnRu intermediate layer. Phys. Rev. B 82, 014423 (2010).
Fullerton, E. E., Jiang, J. S., Grimsditch, M., Sowers, C. H. & Bader, S. D. Exchange-spring behavior in epitaxial hard/soft magnetic bilayers. Phys. Rev. B 58, 12193 (1998).
Victora, R. H. & Shen, X. Exchange coupled composite media for perpendicular magnetic recording. IEEE Trans. Magn. 41, 2828–2833 (2005).
Suess, D. Multilayer exchange spring media for magnetic recording. Appl. Phys. Lett. 89, 113105 (2006).
Donahue, M. J. & Porter, D. G. OOMMF User’s Guide, Interagency Report NISTIR 6376. (National Institute of Standards and Technology, 1999).
Pike, C. R., Roberts, A. P. & Verosub, K. L. Characterizing interactions in fine magnetic particle systems using first order reversal curves. J. Appl. Phys. 85, 6660–6667 (1999).
Davies, J. E. et al. Magnetization reversal of Co/Pt multilayers: Microscopic origin of high-field magnetic irreversibility. Phys. Rev. B 70, 224434 (2004).
Dumas, R. K., Li, C. P., Roshchin, I. V., Schuller, I. K. & Liu, K. Magnetic fingerprints of sub-100 nm Fe dots. Phys. Rev. B 75, 134405 (2007).
Kirby, B. J. et al. Vertically graded anisotropy in Co/Pd multilayers. Phys. Rev. B 81, 100405 (2010).
Rotaru, A. et al. Interactions and reversal-field memory in complex magnetic nanowire arrays. Phys. Rev B. 84, 134431 (2011).
Dobrota, C.-I. & Stancu, A. What does a first-order reversal curve diagram really mean? A study case: Array of ferromagnetic nanowires. J. Appl. Phys. 113, 043928 (2013).
Gilbert, D. A. et al. Quantitative decoding of interactions in tunable nanomagnet arrays using first order reversal curves. Sci. Rep. 4, 4204 (2014).
Davies, J. E. et al. Frustration driven stripe domain formation in Co/Pt multilayer films. Appl. Phys. Lett. 95, 022505 (2009).
Schrefl, T. et al. First order reversal curve studies of permanent magnets. J. Appl. Phys. 111, 07A728 (2012).
Davies, J. E. et al. Reversal mode instability and magnetoresistance in perpendicular (Co/Pd)/Cu/(Co/Ni) pseudo-spin-valves. Appl. Phys. Lett. 103, 022409 (2013).
Dumas, R. K. et al. Accessing different spin-disordered states using first-order reversal curves. Phys. Rev. B 90, 104410 (2014).
Ma, L. et al. Magnetization reversal in perpendicularly magnetized L10 FePd/FePt heterostructures. J. Appl. Phys. 116, 033922 (2014).
Siadou, N. et al. Magnetization reversal in [Ni/Pt]6/Pt(x)/[Co/Pt]6 multilayers. J. Magn. Magn. Mater. 323, 1671 (2011).
Kelly, P., O’Grady, K., Mayo, P. & Chantrell, R. Switching mechanisms in cobalt-phosphorus thin films. IEEE Trans. Magn. 25, 3881–3883 (1989).
Repain, V. et al. Magnetic interactions in dot arrays with perpendicular anisotropy. J. Appl. Phys. 95, 2614–2618 (2004).
Rahman, M. T. et al. Controlling magnetization reversal in Co/Pt nanostructures with perpendicular anisotropy. Appl. Phys. Lett. 94, 042507 (2009).
Hellwig, O., Berger, A., Kortright, J. B. & Fullerton, E. E. Domain structure and magnetization reversal of antiferromagnetically coupled perpendicular anisotropy films. J. Magn. Magn. Mater. 319, 13–55 (2007).
Davies, J. E. et al. Anisotropy-dependence of irreversible switching in Fe/SmCo and FeNi/FePt spring magnet films. Appl. Phys. Lett. 86, 262503 (2005).
Sort, J., Popa, A., Rodmacq, B. & Dieny, B. Exchange-bias properties in permalloy deposited onto a Pt/Co multilayer. Phys. Rev. B 70, 174431 (2004).
Liao, J.-W. et al. Highly (001)-oriented thin continuous L10 FePt film by introducing an FeOx cap layer. Appl. Phys. Lett. 102, 062420 (2013).
Gilbert, D. A. et al. Tuning magnetic anisotropy in (001) oriented L10 (Fe1−xCux)55Pt45 films. Appl. Phys. Lett. 102, 132406 (2013).
Gilbert, D. A. et al. Probing the A1 to L10 transformation in fecupt using the first order reversal curve method. APL Mater. 2, 086106 (2014).
Majkrzak, C. F. Polarized neutron reflectometry. Physica B 173, 75–88 (1991).
Gilbert, D. A. et al. Controllable positive exchange bias via redox-driven oxygen migration. Nature Commun. 7, 11050 (2016).
Gilbert, D. A. et al. Realization of ground-state artificial skyrmion lattices at room temperature. Nature Commun. 6, 8462 (2015).
Kirby, B. J. et al. Phase-sensitive specular neutron reflectometry for imaging the nanometer scale composition depth profile of thin-film materials. Curr. Opin. Colloid Interface Sci. 17, 44–53 (2012).
Weller, D. & McDaniel, T. In Advanced Magnetic Nanostructures (eds D. Sellmyer & R. Skomski ) Ch. 11, 295 (Springer, 2006).
Acknowledgements
This work has been was supported by the NSF (DMR-1008791 and DMR-1543582), BaCaTec (A4 [2012-2]), the France-Berkeley Fund, and DFG (Wi 1828/4-2). Work at NTHU supported by the Ministry of Science and Technology of Republic of China under Grant No. MOST 104-2221-E-007-047-MY2 and MOST 104-2221-E-007-046-MY2. D.A.G. acknowledges support from the National Research Council Research Associateship Program.
Author information
Authors and Affiliations
Contributions
D.A.G. and K.L. conceived and designed the experiments. J.-W.L. and C.-H.L. synthesized the samples. D.A.G. and K.L. performed magnetic characterizations. D.A.G. and B.J.K. carried out PNR investigations. M.W. and D.A.G. did micromagnetic simulations. D.A.G. and K.L. wrote the first draft of the manuscript. K.L. coordinated the project. All authors contributed to discussions and manuscript revision.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Gilbert, D., Liao, JW., Kirby, B. et al. Magnetic Yoking and Tunable Interactions in FePt-Based Hard/Soft Bilayers. Sci Rep 6, 32842 (2016). https://doi.org/10.1038/srep32842
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep32842
This article is cited by
-
Reconstructing phase-resolved hysteresis loops from first-order reversal curves
Scientific Reports (2021)
-
Probing the Transfer of the Exchange Bias Effect by Polarized Neutron Reflectometry
Scientific Reports (2019)
-
The effect of interface anisotropy on demagnetization progress in perpendicularly oriented hard/soft exchange-coupled multilayers
Scientific Reports (2017)
-
Growth-Induced In-Plane Uniaxial Anisotropy in V2O3/Ni Films
Scientific Reports (2017)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.