Abstract
Molecular recognition is rarely a two-body protein-ligand problem, as it often involves the dynamic interplay of multiple molecules that together control the binding process. Myo-inositol monophosphatase (IMPase), a drug target for bipolar disorder, depends on 3 Mg2+ ions as cofactor for its catalytic activity. Although the crystallographic pose of the pre-catalytic complex is well characterized, the binding process by which substrate, cofactor and protein cooperate is essentially unknown. Here, we have characterized cofactor and substrate cooperative binding by means of large-scale molecular dynamics. Our study showed the first and second Mg2+ ions identify the binding pocket with fast kinetics whereas the third ion presents a much higher energy barrier. Substrate binding can occur in cooperation with cofactor, or alone to a binary or ternary cofactor-IMPase complex, although the last scenario occurs several orders of magnitude faster. Our atomic description of the three-body mechanism offers a particularly challenging example of pathway reconstruction, and may prove particularly useful in realistic contexts where water, ions, cofactors or other entities cooperate and modulate the binding process.
Similar content being viewed by others
Introduction
Bipolar disorder is a serious medical illness where episodes of mania alternate with depression. It currently affects more than 254 million people worldwide and is one of the major causes of loss of health and suicide in the middle-aged population1. Since the anti-manic properties of lithium were first reported more than 60 years ago2, it has been the most widely used treatment for bipolar disorder. Unfortunately, the ion’s therapeutic window is very narrow and it is accompanied by severe toxicity issues and side-effects such as tremors, frequent urination, thyroid problems, weight gain and kidney failure3. Therefore, it is desirable to replace it with a more harmless treatment.
The discovery that lithium intake diminishes brain inositol levels4 led to the formulation of the ‘Inositol depletion hypothesis4’ where the ion is proposed to mitigate neurotransmitters in the phosphatidyl inositol (PI) pathway (Fig. 1), overactive in bipolar patients5. Myo-inositol monophosphatase (IMPase) plays a key role in the PI pathway, by hydrolyzing myo-inositol monophosphate (IP). IMPase’s activity in patients suffering from bipolar disorder is assumed to be higher than normal, thus increasing myo-inositol levels. IMPase is also specifically inhibited by therapeutic (0.5–1.5 mM) concentrations of lithium6, and that is why it has been traditionally proposed as the putative target of the inositol depletion theory7,8. Accordingly, IMPase has been the subject of major industrial and academic research for bipolar treatment, and despite the myriad of inhibitors that have been tested over the last years, all have shown poor bioavailability or difficulties to reach the site of action in vivo8,9,10,11,12.
Phospholipase C, activated by G-protein-coupled receptors, hydrolyzes phosphatidylinositol 4,5 biphosphate (PIP2) to produce the two secondary messengers diacylglycerol (DAG) and inositol 1,4,5-triphosphate (IP3), which activate cellular responses. DAG is phosphorylated to give phosphatidic acid (PA) and then ligated to a cytidine giving cytidine monophosphorylphosphatidate (CMP-PA). The latter can be attached to a myo-inositol molecule and form phosphatidylinositol (PI) which can be then converted to PIP2. IP3 then undergoes a series of hydrolysis to generate inositol monophosphates, from which the final hydrolysis of myo-inositol monophosphate (IP) to inositol and inorganic phosphate (Pi) is catalyzed by myo-inositol monophosphatase (IMPase)40. Released free inositol (I) is then recycled into PIP2. IMPase is also involved in the de novo synthesis of inositol by converting glucose-6-phosphate into IP.
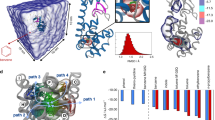
There are two main reasons for the failure in finding a bioavailable drug inhibiting IMPase. Firstly, the structure of IMPase reveals a difficult binding pocket for drug-like compounds. More concretely, mammalian IMPase have been crystalized from murine13, bovine14 and human15 brain and show a homodimer of 60 kDa, with each subunit consisting of a penta-layered αβαβα sandwich formed by alternating 9 α-helices and 13 β-strands (Fig. 2a). The active site of IMPase is a highly hydrophilic cavity lying beneath a β-hairpin region which is thought to play a critical role in the enzyme function16,17,18. To recognize the IP substrate the catalytic cavity is a highly polar pocket which favors polar charged compounds, typically unable to cross the blood-brain barrier (BBB)19. Secondly, although the structural conformation upon substrate and cofactor binding is well defined, its kinetic mechanism is still not clear. A recently solved human crystal IMPase structure in complex with Mg2+ and phosphate showed a catalytic pocket with 3 Mg2+ and superimposable with previous structures13. Mg2+ in site I, to which we will refer as Mg-I throughout this work, binds Glu70, Asp90 the carboxyl group of Ile92, three water molecules and the phosphate group. Mg2+ in site II (Mg-II) is coordinated with Asp90, Asp93, Asp220 the phosphate group and three water molecules, one being shared with Mg-I. The more external Mg2+ site III (Mg-III) is only coordinated by Glu70, the phosphate group and 5 water molecules (Fig. 2b). Different experiments have suggested that the three Mg2+ must occupy the catalytic pocket for the accomplishment of the reaction14,20,21. Attempts to quantify Mg2+ binding showed that the three ions bind with decreasing affinity: Mg-I with a KD of 300 μM22, Mg-II, KD = 3.9 mM23 and low affinity Mg-III. Mg2+ concentration in neurons range from 0.5 to 1 mM and therefore the real occupancy at physiological conditions is unclear24. Whereas some studies proved the enzyme is doubly bound in neurons and the third Mg2+ binds after substrate17, another suggested the presence of three Mg2+ in the absence of substrates14.
(a) Cartoon diagram of the overall folding of one IMPase monomer depicting the penta-layered αβαβα sandwich. Alpha helices are coloured in pink whereas the two sets of beta sheets are shown in white. Mg2+ ions are shown as spheres. (b) The catalytic site showing the three Mg2+ ions. Mg-I is coordinated with Glu70, Asp90, and Ile92 and three water molecules, Mg-II with Asp90, Asp93 and Asp220 and three water molecules, one of them shared with Mg-I. Low-affinity Mg-III interacts with Glu70 and five water molecules.
It is therefore important to determine the mechanism of binding and the most populated states of the protein under physiological conditions in order to provide the basis for the rational design of new inhibitors. Here, we have performed an unprecedented 0.8 milliseconds of all-atom high-throughput molecular dynamics simulations in order to ascertain the concrete mechanism of binding of Mg2+ and the pathway of binding of the natural substrate.
Results
In all in-silico binding analyses, full kinetic and thermodynamic data were obtained by performing free-ligand binding24, all-atom molecular dynamics simulations with the ACEMD25 molecular dynamics software on the distributed computing project GPUGRID26. The data were analysed using the HTMD software27 (available at http://www.htmd.org) and a Markov state modelling (MSM)28 method able to produce quantitative estimations of kon, koff and ∆G0. MSM analyses have been successfully used in a wide range of problems from ligand binding24,29 to the characterisation of protein folding28 and intrinsically disordered protein dynamics30. In this work, we provide a comprehensive study on IMPase enzyme. By means of HTMD, we explain the full picture of cofactor and substrate binding. A total of 6 simulation batches have been performed (Table 1). Four of them focused on understanding the IMPase mode of action in the absence of substrates or inorganic molecules, and the other two, on the natural substrate (IP)’s kinetic mechanism. More details on the specific simulation parameters are provided in the Methods section.
IMPase mode of action in the absence of substrates
Crystallographic studies have shown that there are three Mg2+ ions per subunit in the presence of substrates or inorganic phosphate13,14,15,31. However, some studies have proved IMPase is doubly bound in neurons and the third Mg2+ binds after the substrate17. Given the mild affinities of Mg2+ in site-I and II, and the low Mg2+ concentration in neurons (0.5–1 mM) is unclear what is the occupancy of IMPase prior to substrate binding. Here, we have examined the binding of the three Mg2+ ions by looking at the recognition process one ion at a time (Fig. 3). For the sake of simplicity, we will call binding event of Mg-I as event I, and subsequently event II and event III throughout the study.
Four in-silico experiments were performed to examine the ion’s binding events. (a) Binding of Mg-I to IMPase. One Mg2+ ion was placed around apo-IMPase. The ion bound the pocket with fast kinetics coordinating both I and II site’s residues. Superimposed with the crystal pose, the figure shows Mg-I’s binding mode in pink and the crystallographic ions in green. (b) Binding of Mg-II to IMPase, with Mg-I coordinating sites I and II as obtained in (a). The ion identified the pocket in two distinct poses in this timescale (pink), not corresponding to the crystallographic poses (green, see text). (c) Binding of Mg-III to IMPase at low concentration. 236 μs of simulation time did not show any binding event. (d) Binding of Mg-III to IMPase at high concentration. One binding event per subunit was registered, computing an on-rate of ~105 s−1 M−1. While Mg- I and II recapitulate the expected binding mode (residues in the simulation are shown in cyan, while X-ray residues and ions are shown in green), Mg-III’s binds more loosely interacting with E71.
Binding of Mg-I: event I
For the analysis of event I, one single Mg2+ ion was placed free in solution around the apo-IMPase dimer giving a concentration of 3 mM, at which IMPase is maximally active32. The ion was placed at least 15 Å distance away from the protein in the initial systems’ coordinates, such as it could spontaneously identify its binding pocket without any bias. Using an adaptive sampling scheme33, more than 4500 trajectories of 40 ns were performed in order to compute the binding affinity and rate constants against each of the monomers. We analyzed the event I by performing one independent MSM analysis per subunit (see Methods), which provided remarkably consistent kinetic and affinity estimations between the monomers (Table 2). In quantitative terms, the standard free energy of binding is computed to be −3.8 ± 0.1 kcal/mol, slightly higher than previous dialysis (−4.8 kcal/mol)22 and fluorescence (−4.6 kcal/mol)34 experiments. There are no available crystal structures containing only one Mg2+ bound, however, in binary or ternary complexes Mg-I appears coordinated to three protein residues (Glu70, Asp90, Ile92) and three water molecules. Here, in the absence of Mg-II we observed that it tends to coordinate both characteristic site I and II residues and one single water molecule (Fig. 3). The transition to this pose occurs with very fast kinetics, in the order of 108 M−1 s−1.
Binding of Mg-II: event II
Reconstruction of event II was performed in a similar fashion. Mg-I was placed on each monomer coordinating both site I and II residues as obtained in event I’s analysis. Then a single Mg-II ion was placed free in solution, at least 15 Å distance from the protein. Accounting for three total Mg2+ ions, the concentration was 8 mM. We then performed another MSM analysis per monomer, as previously done for event I’s analysis. The analysis provided two poses with similar affinity in the first monomer, whereas in the other we lacked statistics to get a converged model. Looking at the first monomer’s poses, it was observed Mg-II tended to approach the catalytic pocket by interacting in two different binding sites other than the crystallographic one, as was site-II in coordination with Mg-I. Both poses are in the vicinity of Mg-I, the first interacting with Glu213, and the other with Glu71 (Fig. 3b, event II). We then analyzed Mg-I’s stability, in order to see transitions towards the crystallographic site. Taking into account the 277 μs produced in this and the previous set, we performed a root mean squared deviation (RMSD) of Mg-I aligning all Cα atoms in the protein against the crystal coordinates in 4AS413. Only in 4 trajectories out of more than 5000, Mg-I evolved to the crystallographic position with an RMSD lower than 1 Å. Thorne et al. performed stopped-flow fluorescence spectroscopy studies to determine association and dissociation constants for Mg-I and II34. The study showed a slow increase in fluorescence after a rapid binding of Mg-I, suggesting that Mg-I binding is followed by a subtle structural rearrangement in the microenvironment of site I. The obtained on-rate was 4.4 ± 0.18·105 M−1 s−1, whereas our estimates for Mg-I’s kinetics revealed a much faster process. Hence, event I showed very fast kinetics in our experiment, and our analysis did not recover the crystal pose, contrary to the equilibrium-based fluorescence experiments. Although our pose and the crystallographic one are only 3.3 Å RMSD away, subtle differences in neighboring atoms confer completely different octahedral coordination for Mg-I. We argue that the rearrangement of the negatively charged residues around these ions needed to reach its exact coordination found in X-ray is plausibly a much slower process in line with the experimental observations. Note that given the experimental kinetics, in order to sample such slow rearrangements, it would be needed to produce multi-millisecond simulations length that is beyond current capabilities.
Binding of Mg-III: event III
For the analysis of event III, 236 μs of simulation time were produced. Mg-III was placed around IMPase, whereas Mg-I and II were located in their X-ray sites in both subunits this time, as the rearrangement to crystallographic positions was shown to be a very slow process. Interestingly, performing an RMSD analysis of the 3900 trajectories against the coordinates in 4AS413 did not provide any spontaneous event III under these low concentration conditions. By performing an MSM analysis, we observed that at this concentration and timescale Mg-III binds at the interface between monomers (Fig. S1). Anticipating that event III is governed by very slow kinetics, we increased the concentration to 54 mM, with a total of 20 Mg2+ ions in the box. In 100 μs of simulation time, only 1 complete binding event was recovered per monomer, providing an RMSD of 2 Å to the crystal position of Mg-III13. The computed binding frequency is of the order of 0.01 μs−1, which, taking into account the concentration yields an on-rate of 1.85·105 M−1 s−1.
Mg2+ is known to exert a bimodal activation on IMPase depending on its concentration. At low concentrations, as in neurons, Mg2+ acts as an activator being maximally active at 1 mM. At higher concentrations (>20 mM), it acts as non-competitive inhibitor. We performed our simulations at concentrations at which IMPase would only have residual activity hydrolyzing IP. However, inhibition by high concentrations is thought to be due to product trapping31,32,35. In a recent crystallographic study, it was concluded that both Li+ and Mg2+ do not interfere with the catalytic reaction, but stabilize the post-catalytic complex instead31. These data taken together, suggest that Mg-III can bind to IMPase to form a ternary complex even in the absence of inorganic phosphate, natural substrates or inhibitors, but we cannot estimate the affinity due to the millisecond binding timescale.
Substrate pathway reconstruction
IMPase’s catalytic mechanism on IP’s hydrolysis has been the subject of several studies. For many years, the enzyme was thought to operate via two Mg2+ ions. Pollack et al.16 proposed a mechanism in which Mg-I acted as the water nucleophile activator while Mg-II as a stabilizer for the leaving inositol. More recent observations have favored a hydrolysis operating via three Mg2+ ions instead20. Despite the pre-catalytic complex being well characterized, the steps leading to its formation are not yet clear. Whereas some studies supported a random mechanism22, others inclined towards an ordered mechanism, with the substrate binding IMPase, and only Mg-III binding after17. Some other studies favored the presence of three Mg2+ in the absence of substrates14.
Assuming that once each of the Mg2+ ions binds in their corresponding positions and remain stable for timescales much longer than the substrate binding, we can consider bound ions as virtually covalent. For simplicity, we will refer to the protein states in which there are two and three Mg2+ bound per subunit as IMPase-II and IMPase-III. The exchange between IMPase-II and IMPase-III occurs in very long timescales, up to several milliseconds. This leads to a partition of IMPase’s conformational space into two different kinetic pathways. The binding of the natural substrate could present different relative affinities for IMPase-II and IMPase-III, leading to conformational selection36, and could be able to shift the equilibrium towards any of the conformers by induced-fit37.
In order to understand the sequence of events prior to the formation of the pre-catalytic complex, the binding was performed against these two protein states. The first system contained IMPase-II, and the two remaining Mg2+ corresponding to site III were randomly placed in solution. The second system contained IMPase-III, no Mg2+ ions present in bulk. A total of five IP molecules were placed around the enzyme in both cases. The final substrate and ion concentration were set to 12 and 5 mM, respectively. The two systems were therefore thermodynamically identical.
Taking into account the two systems, 155.8 μs of total sampling time was produced. The IP molecules carry two negative charges in the phosphate group, and therefore the interaction with other ligand molecules is avoided by electrostatic repulsion. Still, the ligands performed short-lived interactions among themselves or through Mg2+ bridges, the same way it could be expected in an experiment at this concentration. For our analysis, we treated each ligand interaction against IMPase as an independent trajectory from other ligands. The results show many IP binding events to IMPase-III and to IMPase-II, in coordination with Mg2+ or alone. In order to understand the main pathways of binding and provide kinetic estimates, an MSM was produced gathering the two simulation sets. In this analysis, the contacts between substrate and protein were mapped and geometrically clustered. After, each cluster was further split taking into account whether the Mg2+ ion was coordinated or not with IP’s phosphate group at a shorter distance than 4 Å (see Methods).
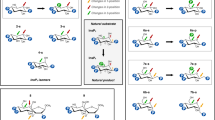
Five final states showing IP free in solution, bound, or in metastable states were obtained. Figure 4b summarizes the transitions among them and their specific binding modes. State 1, corresponds to bulk or the initial state in the reaction pathway, that is to say, when IP is free in solution. State 2, located at the interface between subunits, does not directly convert to the other states without reverting to bulk. This binding pose is independent of IMPase’s coordination and occurs both in IMPase-II and III. IP does not interact to any Mg2+ ion in this pose. States 3 and 4, correspond to short-lived states in the pathway of IP binding. Lastly, state 5, corresponds to the bound pose in the catalytic pocket of IMPase-III. The pose obtained through our analysis, overlaps well with the crystal structure (Fig. 5). Under the case of a conventional non-covalent reversible binding, IP would bind with a Gibbs free energy of −7.1 ± 0.3 kcal/mol, as computed as the ratio between its off and on rates. Once bound, state 5 presents a residence time of several milliseconds. IMPase’s kcat is 22 + 3 s−1 at 0.5 mM IP concentration, and therefore hydrolyzes an IP molecule in 45 ms. With this turnover number, IMPase-III plausibly hydrolyzes IP molecules once they have reached state 5, shifting metastable states 3 and 4 towards the bound pose. Full kinetic and quantitative data is presented in Table S1.
(a) In the absence of substrate (IP), the conversion between the two IMPase conformers takes several milliseconds. (b) In the presence of substrate, the latter binds with very fast kinetics in a one-step mechanism to IMPase-III (state 5). The substrate is also able to bind IMPase-II in a two-step reaction by two different pathways. In the first case, it binds in a complex with Mg-III in the low millisecond timescale (state 4). It quickly rearranges to the crystal pose. In the second case, it binds to IMPase-II (state 3) in a pose distant from the Mg2+ dyad. It then rapidly acquires one free Mg-III and converts to the crystal pose.
20. Shown in green, the three ions, Ca2+ for the crystal structure (shown in a thinner representation), Mg2+ in our simulations (bulkier with labels on them). In cyan, the substrate IP, and in white the protein as obtained from simulations (MSM). Superimposed in a thinner representation using the same coloring method the substrate coordinates in 1AWB pdb. The protein residues coordinating the ions correspond to the simulations. The RMSD for this pose, taking into account the substrate heavy atoms, was 4.5 Å. (Fig. 4b, state 5).
IP can reach the bound state through three different pathways of binding. The fastest binding route corresponds to the direct binding to IMPase-III from bulk. The average binding occurs in a time between 2.6 and 5.8 μs. A second, slower binding pathway consists on a two-step binding mechanism. The first rate-limiting step comprises the binding of the IP-Mg-III complex to IMPase-II’s catalytic pocket, occurring in 0.8–3.4 ms (state 4). Visual inspection of the trajectories leading to this state showed that although IP-Mg-III reaches the pocket as a complex, once inside the protein residues are able to dissociate the complex more than 4 Å apart. Thus, the MSM analysis detected a state represented by Mg-III and IP in disordered positions inside IMPase-II’s pocket. The formation of this metastable state is followed by a quick reordering of the complex towards the bound pose in 1–2 μs. The third, slowest mechanism consists on the binding IP alone to the vicinities of the catalytic pocket (state 3), with a time about 1–10 ms, followed by a much faster step occurring in a few microseconds. The longer rearrangement times for this third pathway regarding the second could be due to the formation of di-IP-Mg2+ complexes or the longer distance to the active site.
Looking at the different binding pathways in relative terms, we see that the first, single-step binding pathway occurs three orders of magnitude faster than the two others, and could in practical terms be the only pathway of binding. Assuming equal populations of the two IMPase forms, the substrate could reach the pre-hydrolysis pose over one thousand times through the direct pathway in the time it would need through the second or third pathways. Note, however, that the real populations of IMPase-II and IMPase-III remain unknown. We never observed the Mg-III’s unbinding event and neither the off-rate nor the equilibrium constant can be estimated or are present in literature.
From the binding event, we have estimated that the shift from IMPase-II to IMPase-III takes several milliseconds in the absence of IP, as deduced from the process’ on-rate of 1.85 · 105 M−1 s−1 (Fig. 4a). However, in the presence of IP, the equilibrium is shifted to the right: once the substrate is bound to IMPase-II, the cofactor reaches site III in a few microseconds. These facts can easily be explained in terms of electrostatic repulsion. apo-IMPase presents a highly polar pocket composed by four acidic residues (Glu70, Asp90, Asp93, and Asp220), totaling up to four negative charges in close vicinity. The binding of Mg-I and Mg-II, each carrying two positive charges, neutralizes the pocket. The binding of Mg-III under these conditions would in principle not be very favorable, thus explaining its very slow kinetics. However, the natural substrate presents two negative charges on its phosphate group. The great differences we observe for substrate binding to IMPase-II and IMPase-III are also possibly a consequence of the pocket’s total charge differences: whereas IP’s binding to the doubly positively charged IMPase-III’s pocket is diffusion-controlled, the binding to neutral IMPase-II’s pocket takes a few milliseconds regardless its pathway.
Discussion
We have fully characterized substrate and cofactor binding prior to the catalytic event. The first study concluded that the protein is able to form a ternary complex with Mg2+ ions, even in the absence of substrate, inhibitors or inorganic phosphate, but its population could not be reliably measured. Our study shows that Mg-I and II’s pocket identification is diffusion limited, whereas subsequent rearrangement of coordinating residues takes several milliseconds. The binding of Mg-III, although difficult to observe at physiological concentrations, could be recorded at 20 mM, giving a mean first passage time (mfpt) estimation of around 50 ms at 1 mM.
We have also provided an atomic-level description of substrate and cofactor cooperation and binding. IP is able to bind both IMPase-II and III forms to different extents. The substrate shows a very fast binding, occurring in a mean time of 4 μs, to IMPase-III. Additionally, the molecule is also able to bind to IMPase-II although in a slower fashion. Both either accompanied by Mg-III or alone it identifies IMPase-II in a millisecond two-step reaction. Interestingly, although event III is very difficult to observe even in high-throughput simulations as done here, the process speeds up by 3 orders of magnitude in the presence of IP. These facts are easily supported by the drastic net charge changes at IMPase’s pocket.
The mechanism presented complements previous studies on deciphering the order of substrate and cofactor binding. The most recent proposed studies agreed with the Leech et al.’s ordered mechanism, with substrate binding first and modifying or creating the binding site for one or two metals binding after38. However, this mechanism did not account with the 3-metal structures that later emerged39; and subsequent analysis proposed cofactor binding before and after substrate binding17,32. Our mechanism shows that substrate binding after cofactor is kinetically favored, however we have shown that cofactor binding before and along with substrate is also possible, and could be the only pathway in the scenario where IMPase-III’s population was marginal. Actually, the versatility here presented could explain the diversity in previous studies, and those which observed a random-ordered mechanism35,40. Biochemical experimental studies on IMPase’s gained a lot of attention two decades ago, however, difficulties to design bioavailable inhibitors prompted research on IMPase’s to come to a halt. We hope that future experiments can further progress our understanding of IMPase’s function and in particular help characterize the IMPase conformational space. We have used arguably the most advanced computational methods and infrastructure for exploring enzyme dynamics and whilst we are limited by the use of empirical force fields and possible difficulties of parameterization, we have been able to shed light onto important biochemical questions arising from previous experimental work. We note, however, that the picture of binding presented here, although capturing the different substrate binding routes, is only a portion of the complete conformational space. In particular, IMPase is known to present two segments in the entrance of its catalytic pocket (the β-hairpin region comprised by residues 30–40 and the short helix comprised by residues 70–75) which appear to be disordered in the absence of ions, and could undergo several rearrangements upon substrate and metal binding17,39. We have, of course, observed protein plasticity along all the simulation sets performed in these regions. Nevertheless, given all our structures started from active conformation such movements are not representative of the global protein conformation space. Helix and β-sheets formation occur at timescales much slower41 than our ensembles and we do not have enough data at this stage to provide a solid study on the role such segments.
In summary, we have used large-scale HTMD and been able to recapitulate the binding events of Mg ions and natural substrate at IMPase, and we identified structures close to the X-ray solutions. In addition, our methodology also provides important information about the competition, cooperativity and kinetics of the binding pathways in this complex three-body process. We propose that the pathway diversity seen here might not be a particular case of IMPase, but a general principle for ligand binding. The ligand-binding paradigm is rarely a two-body problem (drug and receptor) because, water, or in particular ions, can play a critical role. We note that the quantitative study of IMPase’s mode of action is a particularly challenging case. The highly polar nature of the enzyme’s pocket, the metal parameterization, long timescales of the processes and the three-body mechanism of binding might not be the case of other targets. Still, with the advances in computational infrastructure, forcefield and analysis methods we believe that this approach can provide insight to understanding binding pathways for difficult targets like this. We expect that in the near future approaches similar to the one presented will become common in the early stage of the drug discovery pipeline. Such a study can provide a deeper understanding of the binding processes and the endogenous population of the active site, essential aspects of lead finding and optimization.
Material and Methods
Simulation system setup and simulation parameters
Input coordinates for human IMPase protein were based on the PDB code 4AS413. The AMBER FF12SB42 forcefield was used to describe all the protein parameters. Mg2+ parameters were taken from a previous study43 where the parameters were fitted against experimental data in order to provide a better description of their kinetic properties in water, also improving the phosphate binding description. All chemical entities were protonated with the OpenBabel software at pH 7.444 and parameterized by the Antechamber 12 tool45. All the complexes were explicitly solvated by the LEAP module of the AMBER 12 software package in a TIP3P46 cubic water box with at least 12 Å distance around the complex and then electrically neutralized using K+ and Cl− ions. The final size of the systems was about 90000 atoms. The different cofactor and substrate concentrations are specified in Table 1.
Each system was minimized and relaxed under NPT conditions for 1 ns at 1atm and 298 K using a time-step of 4 fs, rigid bonds, a cut-off of 9 Å and PME for long-range electrostatics. Heavy protein and ligand atoms were constrained by a 1 kcal/mol/Å2 spring constant during the equilibrations and gradually reduced. Production simulations were run using ACEMD over GPUGRID47 in the NVT ensemble using a Langevin thermostat with damping of 0.1 ps−1 and hydrogen mass repartitioning scheme to achieve timesteps of 4 fs48. The total simulation times are summarized in Table 1.
Markov State Models
A Markov state model (MSM) for each of the systems was built from the molecular simulation trajectories. MSMs have been successfully used to reconstruct the equilibrium and kinetic properties in a large number of molecular systems24,49,50. By determining the frequency of transitions between conformational states we were able to construct a master equation which describes the dynamics between a set of conformational states. Relevant states are determined geometrically by clustering the simulation data onto a metric space (e.g. contact maps). In this case, a discrete description of the process was obtained by means of protein-ligand contact maps. The carbon alpha atoms in the protein and the Mg2+ atom or the heavy atoms for the substrate molecule were selected for the construction of contact maps along all the trajectories. Two atoms are in contact if their distance is less than 8 Å.
One of the most important requirements for constructing Markov models is to be able to finely discretize the slowest order parameters. TICA51 (time-lagged independent component analysis) is a method that projects the data on the slow order parameters, thus producing a very good discretization. After projecting the high-dimensional protein-ligand contact maps onto the three slowest processes found by TICA with a 2 ns lag-time, the n-dimensional projected data was clustered using the k-centers algorithm. 3 and 5-dimensional projections were used for the analysis of Mg2+ binding and pathway reconstruction. The master equation is then built as

where Pi(t) is the probability of state i at time t, and kij are the transition rates from j to i, and K = (Kij) is the rate matrix with elements Kij = kij for i ≠ j and  . The master equation dP/dt = K P has solution with initial condition P(0) given by P(t) = T(t) P(0), where we defined the transition probability matrix Tij(t) = (exp[Kt])ij = p(i,t|j,0), i.e. the probability of being in state i at time t, given that the system was in state j at time 0. In practical terms, pij(Δt) is estimated from the simulation trajectories for a given lag time Δt using a maximum likelihood estimator compatible with detailed balance52. The eigenvector π with eigenvalue 1 of the matrix T(Δt) corresponds to the stationary, equilibrium probability. Higher eigenvectors correspond to exponentially decaying relaxation modes for which the relaxation timescale is computed by the eigenvalue as
. The master equation dP/dt = K P has solution with initial condition P(0) given by P(t) = T(t) P(0), where we defined the transition probability matrix Tij(t) = (exp[Kt])ij = p(i,t|j,0), i.e. the probability of being in state i at time t, given that the system was in state j at time 0. In practical terms, pij(Δt) is estimated from the simulation trajectories for a given lag time Δt using a maximum likelihood estimator compatible with detailed balance52. The eigenvector π with eigenvalue 1 of the matrix T(Δt) corresponds to the stationary, equilibrium probability. Higher eigenvectors correspond to exponentially decaying relaxation modes for which the relaxation timescale is computed by the eigenvalue as  , where λs is to the largest eigenvalue above 1. For long enough lag times the model will be Markovian, however every process faster than Δt is lost. Therefore, the shortest lag is chosen for which the relaxation timescales do not show a dependence on the lag time Δt anymore. In our case, we chose different lag times depending on the system, provided a good compromise between convergence in the implied timescale while being short enough to allow for sufficient statistical variance. Implied timescales and chosen lag times are shown in Table S2. Furthermore, although this fine discretization provides very good Markov models, it is necessary to reduce the amount of states to obtain a humanly interpretable model of the system in question. Therefore, the initial microstates can be lumped together into macrostates using kinetic information from the MSM eigenvector structure. Mean first passage times and commitor probabilities can also be calculated to obtain the relevant kinetics of the system53. Hence, the produced clusters were then lumped together into macrostates using the PCCA algorithm, each consisting of a set of kinetically similar clusters. For the specific case of substrate pathway binding, the analysis was performed as follows. The 3870 trajectories were split into five independent IP trajectories, as each simulation comprised five molecules. This set contained 7801920 frames, each of which was transformed into a ligand-protein alpha carbon contact map where two atoms were considered in contact when closer than 8 Å. After performing a TICA projection onto the 5 slowest order parameters, the data was geometrically clustered using the k-centers algorithm into 925 clusters. Each of these clusters was further split taking into account if the substrate’s phosphate group was in contact with any of the two Mg-III ions or not. 26 new clusters were created giving a total of 951 clusters, which were subsequently used in the MSM model. The microstates were finally combined into 5 macrostates by PCCA, and their transitions and binding modes are represented in Fig. 4b and Table S1. Only bulk, state 4 and 5 contained clusters in which Mg2+ and IP were in contact.
, where λs is to the largest eigenvalue above 1. For long enough lag times the model will be Markovian, however every process faster than Δt is lost. Therefore, the shortest lag is chosen for which the relaxation timescales do not show a dependence on the lag time Δt anymore. In our case, we chose different lag times depending on the system, provided a good compromise between convergence in the implied timescale while being short enough to allow for sufficient statistical variance. Implied timescales and chosen lag times are shown in Table S2. Furthermore, although this fine discretization provides very good Markov models, it is necessary to reduce the amount of states to obtain a humanly interpretable model of the system in question. Therefore, the initial microstates can be lumped together into macrostates using kinetic information from the MSM eigenvector structure. Mean first passage times and commitor probabilities can also be calculated to obtain the relevant kinetics of the system53. Hence, the produced clusters were then lumped together into macrostates using the PCCA algorithm, each consisting of a set of kinetically similar clusters. For the specific case of substrate pathway binding, the analysis was performed as follows. The 3870 trajectories were split into five independent IP trajectories, as each simulation comprised five molecules. This set contained 7801920 frames, each of which was transformed into a ligand-protein alpha carbon contact map where two atoms were considered in contact when closer than 8 Å. After performing a TICA projection onto the 5 slowest order parameters, the data was geometrically clustered using the k-centers algorithm into 925 clusters. Each of these clusters was further split taking into account if the substrate’s phosphate group was in contact with any of the two Mg-III ions or not. 26 new clusters were created giving a total of 951 clusters, which were subsequently used in the MSM model. The microstates were finally combined into 5 macrostates by PCCA, and their transitions and binding modes are represented in Fig. 4b and Table S1. Only bulk, state 4 and 5 contained clusters in which Mg2+ and IP were in contact.
Errors were estimated for all properties using a bootstrapping technique. We performed 7 independent runs in which 20% of the trajectories were randomly eliminated and a new MSM was built after re-clustering. On each of these runs, the same parameters as described above were applied.
Additional Information
How to cite this article: Ferruz, N. et al. Multibody cofactor and substrate molecular recognition in the myo-inositol monophosphatase enzyme. Sci. Rep. 6, 30275; doi: 10.1038/srep30275 (2016).
References
Equilibrium-The bipolar foundation.
CADE, J. F. J. Lithium salts in the treatment of psychotic excitement. Med. J. Aust. 2, 349–352 (1949).
Atack, J. R., Broughton, H. B. & Pollack, S. J. Inositol monophosphatase–a putative target for Li+ in the treatment of bipolar disorder. Trends Neurosci. 18, 343–349 (1995).
Berridge, M. J., Downes, C. P. & Hanley, M. R. Neural and developmental actions of lithium: a unifying hypothesis. Cell 59, 411–419 (1989).
Harwood, A. J. Lithium and bipolar mood disorder: the inositol-depletion hypothesis revisited. Mol. Psychiatry 10, 117–126 (2004).
Hallcher, L. M. & Sherman, W. R. The effects of lithium ion and other agents on the activity of myo-inositol-1-phosphatase from bovine brain. J. Biol. Chem. 255, 10896–10901 (1980).
Pollack, S. J. et al. Mechanism of inositol monophosphatase, the putative target of lithium therapy. Proc. Natl. Acad. Sci. USA 91, 5766–5770 (1994).
Fauroux, C. M. J. & Freeman, S. Inhibitors of Inositol Monophosphatase. J. Enzyme Inhib. Med. Chem. 14, 97–108 (1999).
Atack, J. R. Inositol monophosphatase inhibitors—lithium mimetics? Med. Res. Rev. 17, 215–224 (1997).
Piettre, S. R., Ganzhorn, A., Hoflack, J., Islam, K. & Hornsperger, J.-M. α-Hydroxytropolones: A New Class of Potent Inhibitors of Inositol Monophosphatase and Other Bimetallic Enzymes. J. Am. Chem. Soc. 119, 3201–3204 (1997).
Bashir-Uddin Surfraz, M., Miller, D. J., Gani, D. & Allemann, R. K. Product-like inhibitors of inositol monophosphatase. Tetrahedron Lett. 44, 7677–7679 (2003).
Miller, D. J., Bashir-Uddin Surfraz, M., Akhtar, M., Gani, D. & Allemann, R. K. Removal of the phosphate group in mechanism-based inhibitors of inositol monophosphatase leads to unusual inhibitory activity. Org. Biomol. Chem. 2, 671–688 (2004).
Singh, N. et al. Cloning, expression, purification, crystallization and X-ray analysis of inositol monophosphatase from Mus musculus and Homo sapiens. Acta Crystallograph. Sect. F Struct. Biol. Cryst. Commun. 68, 1149–1152 (2012).
Gill, R. et al. High-resolution structure of myo-inositol monophosphatase, the putative target of lithium therapy. Acta Crystallogr. D Biol. Crystallogr 61, 545–555 (2005).
Bone, R., Springer, J. P. & Atack, J. R. Structure of inositol monophosphatase, the putative target of lithium therapy. Proc. Natl. Acad. Sci. USA 89, 10031–10035 (1992).
Atack, J. R., Broughton, H. B. & Pollack, S. J. Structure and mechanism of inositol monophosphatase. FEBS Lett. 361, 1–7 (1995).
Ganzhorn, A. J. et al. The contribution of lysine-36 to catalysis by human myo-inositol monophosphatase. Biochemistry (Mosc.) 35, 10957–10966 (1996).
Whiting, P., Gee, N. S., Potter, J., Howell, S. & Ragan, C. I. Limited proteolysis and ‘in vitro’ mutagenesis of bovine brain inositol monophosphatase identifies an N-terminal region important for activity. Biochem. J. 272, 465–468 (1990).
Miller, D. J. & Allemann, R. K. myo-Inositol monophosphatase: a challenging target for mood stabilising drugs. Mini Rev. Med. Chem. 7, 107–113 (2007).
Ganzhorn, A. J. & Rondeau, J.-M. Structure of an Enzyme-Substrate Complex and the Catalytic Mechanism of Human Brain Myo-Inositol Monophosphatase. Protein Eng 10, 61–null (1997).
Lu, S. et al. Insights into the role of magnesium triad in myo-inositol monophosphatase: metal mechanism, substrate binding, and lithium therapy. J. Chem. Inf. Model. 52, 2398–2409 (2012).
Greasley, P. J., Hunt, L. G. & Gore, M. G. Bovine inositol monophosphatase. Ligand binding to pyrene-maleimide-labelled enzyme. Eur. J. Biochem. FEBS 222, 453–460 (1994).
Rees-Milton, K., Thorne, M., Greasley, P., Churchich, J. & Gore, M. G. Detection of metal binding to bovine inositol monophosphatase by changes in the near and far ultraviolet regions of the CD spectrum. Eur. J. Biochem. FEBS 246, 211–217 (1997).
Buch, I., Giorgino, T. & De Fabritiis, G. Complete reconstruction of an enzyme-inhibitor binding process by molecular dynamics simulations. Proc. Natl. Acad. Sci. 108, 10184–10189 (2011).
Harvey, M. J., Giupponi, G. & Fabritiis, G. D. ACEMD: Accelerating Biomolecular Dynamics in the Microsecond Time Scale. J. Chem. Theory Comput. 5, 1632–1639 (2009).
Buch, I., Harvey, M. J., Giorgino, T., Anderson, D. P. & De Fabritiis, G. High-Throughput All-Atom Molecular Dynamics Simulations Using Distributed Computing. J. Chem. Inf. Model. 50, 397–403 (2010).
Doerr, S., Harvey, M. J., Noé, F., De Fabritiis, G. HTMD: High-throughput molecular dynamics for molecular discovery, J. Chem. Theory Comput, 12(4), 1845–1852 (2016).
Voelz, V. A., Bowman, G. R., Beauchamp, K. & Pande, V. S. Molecular simulation of ab initio protein folding for a millisecond folder NTL9(1–39). J. Am. Chem. Soc. 132, 1526–1528 (2010).
Held, M. & Noé, F. Calculating kinetics and pathways of protein–ligand association. Eur. J. Cell Biol. 91, 357–364 (2012).
Stanley, N., Esteban-Martín, S. & De Fabritiis, G. Kinetic modulation of a disordered protein domain by phosphorylation. Nat. Commun. 5, (2014).
Dutta, A., Bhattacharyya, S., Dutta, D. & Das, A. K. Structural elucidation of the binding site and mode of inhibition of Li(+) and Mg(2+) in inositol monophosphatase. FEBS J. 281, 5309–5324 (2014).
Strasser, F., Pelton, P. D. & Ganzhorn, A. J. Kinetic characterization of enzyme forms involved in metal ion activation and inhibition of myo-inositol monophosphatase. Biochem. J. 307 (Pt 2), 585–593 (1995).
Doerr, S. & De Fabritiis, G. On-the-Fly Learning and Sampling of Ligand Binding by High-Throughput Molecular Simulations. J. Chem. Theory Comput. doi: 10.1021/ct400919u (2014).
Thorne, M. R., Greasley, P. J. & Gore, M. G. Bovine inositol monophosphatase: enzyme-metal-ion interactions studied by pre-equilibrium fluorescence spectroscopy. Biochem. J. 315 (Pt 3), 989–994 (1996).
Ganzhorn, A. J. & Chanal, M. C. Kinetic studies with myo-inositol monophosphatase from bovine brain. Biochemistry (Mosc.) 29, 6065–6071 (1990).
Weikl, T. R. & Paul, F. Conformational selection in protein binding and function. Protein Sci. Publ. Protein Soc. 23, 1508–1518 (2014).
Boehr, D. D., Nussinov, R. & Wright, P. E. The role of dynamic conformational ensembles in biomolecular recognition. Nat Chem Biol 5, 789–796 (2009).
Leech, A. P., Baker, G. R., Shute, J. K., Cohen, M. A. & Gani, D. Chemical and kinetic mechanism of the inositol monophosphatase reaction and its inhibition by Li+ Eur. J. Biochem. FEBS 212, 693–704 (1993).
Bone, R. et al. Structural analysis of inositol monophosphatase complexes with substrates. Biochemistry (Mosc.) 33, 9460–9467 (1994).
Gee, N. S. et al. The purification and properties of myo-inositol monophosphatase from bovine brain. Biochem. J. 249, 883–889 (1988).
Kalyaanamoorthy, S. & Chen, Y.-P. P. Modelling and enhanced molecular dynamics to steer structure-based drug discovery. Prog. Biophys. Mol. Biol. 114, 123–136 (2014).
Hornak, V. et al. Comparison of multiple Amber force fields and development of improved protein backbone parameters. Proteins 65, 712–725 (2006).
Allnér, O., Nilsson, L. & Villa, A. Magnesium Ion–Water Coordination and Exchange in Biomolecular Simulations. J. Chem. Theory Comput. 8, 1493–1502 (2012).
O’Boyle, N. M. et al. Open Babel: An open chemical toolbox. J. Cheminformatics 3, 33 (2011).
Case, D. A. et al. The Amber biomolecular simulation programs. J. Comput. Chem. 26, 1668–1688 (2005).
Mark, P. & Nilsson, L. Structure and Dynamics of the TIP3P, SPC, and SPC/E Water Models at 298 K. J Phys Chem A 105, 9954–9960 (2001).
Fabritiis, G. D. The GPUGRID.org website. http://www.gpugrid.org/.
Feenstra, K. A., Hess, B. & Berendsen, H. J. C. Improving efficiency of large time-scale molecular dynamics simulations of hydrogen-rich systems. J. Comput. Chem. 20, 786–798 (1999).
Sadiq, S. K., Noé, F. & Fabritiis, G. D. Kinetic characterization of the critical step in HIV-1 protease maturation. Proc. Natl. Acad. Sci., doi: 10.1073/pnas.1210983109 (2012).
Pan, A. C. & Roux, B. Building Markov state models along pathways to determine free energies and rates of transitions. J. Chem. Phys. 129, 064107 (2008).
Pérez-Hernández, G., Paul, F., Giorgino, T., De Fabritiis, G. & Noé, F. Identification of slow molecular order parameters for Markov model construction. J. Chem. Phys. 139, 015102 (2013).
Prinz, J.-H. et al. Markov models of molecular kinetics: Generation and validation. J. Chem. Phys. 134, 174105–174105–23 (2011).
Singhal, N., Snow, C. D. & Pande, V. S. Using path sampling to build better Markovian state models: Predicting the folding rate and mechanism of a tryptophan zipper beta hairpin. J. Chem. Phys. 121, 415 (2004).
Acknowledgements
NF acknowledges support from Generalitat de Catalunya (FI-Agaur). GDF acknowledges support from MINECO (BIO2014-53095-P) and FEDER.We also thank all the volunteers of GPUGRID who donated GPU computing time to the project.
Author information
Authors and Affiliations
Contributions
N.F. built the systems, analysed the data and wrote the manuscript, G.T. designed the project, A.P.L. revised the manuscript and provided experimental guidance and G.D.F. wrote part of the software, supervised the project and revised the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Ferruz, N., Tresadern, G., Pineda-Lucena, A. et al. Multibody cofactor and substrate molecular recognition in the myo-inositol monophosphatase enzyme. Sci Rep 6, 30275 (2016). https://doi.org/10.1038/srep30275
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep30275
This article is cited by
-
Metabolic profiling reveals glucose and fructose accumulation in gcr1 knock-out mutant of Arabidopsis
Applied Biological Chemistry (2019)
-
Dopamine D3 receptor antagonist reveals a cryptic pocket in aminergic GPCRs
Scientific Reports (2018)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.