Abstract
Thanks to the digital revolution, digital signal processing and control has been widely used in many areas of science and engineering today. It provides practical and powerful tools to model, simulate, analyze, design, measure and control complex and dynamic systems such as robots and aircrafts. Gene networks are also complex dynamic systems which can be studied via digital signal processing and control. Unlike conventional computational methods, this approach is capable of not only modeling but also controlling gene networks since the experimental environment is mostly digital today. The overall aim of this article is to introduce digital signal processing and control as a useful tool for the study of gene networks.
Similar content being viewed by others
Introduction
Digital signal processing and control engineering has been widely used in many areas of science and engineering today1,2. It enables our “digital society” and its applications are vast. This popularity is a result of the significant advances in digital computer technology. Complex signal processing and control tasks, which are usually too difficult and/or too expensive to be performed by analog systems, can be performed by less expensive and often more reliable digital computers. Furthermore, digital signal processing and control algorithms provide a greater degree of flexibility as they are programmable. In this context, there has been an explosive growth in digital signal processing and control theory and applications over the past decades. In this article, it is proposed the digital approach can be useful for the study of gene networks. Unlike conventional modeling approaches such as Boolean networks, Bayesian networks, Petri nets, ordinary differential equations and stochastic simulation algorithms (reviewed in3), digital signal processing and control can be used not only to model, simulate and analyze gene networks but also to interact with them in real time as experimental data are mostly digital today. Analog or continuous experimental data are sampled or discretized at discrete time points (analog-to-digital conversion) and processed to generate digital control signals, which are transformed into analog signals through digital-to-analog conversion (Fig. 1A). While calculus-based differential equations dominate in continuous domain, discrete-time difference equations, which require only addition and multiplication, become useful in digital domain1,2. Difference equations have been extremely powerful in computational science and engineering due to this simplicity4. They are typically generated by discretizing continuous differential equations using various approaches such as the Euler and Runge-Kutta methods5. This approach is based on the assumption that continuous models better reflect reality and difference equations can be used to “approximate” those continuous models. Approximation or discretization error can be decreased by increasing the discretization resolution or the sampling frequency. In this article, an alternative approach is proposed as gene network dynamics are inherently discrete in nature. For example, there is no such thing as 1.02437 protein molecule. The amount of protein molecules present in cells is always a discrete integer number. In addition, the production of each protein molecule requires a discrete amount of time. In this context, it is proposed that difference equations can be used to model gene network dynamics, which approximate not continuous differential equations but real systems. This approach is not only simpler but also more accessible to students and researchers not familiar with differential equations since the mathematics is simple to understand. Similar to the first approach, the approximation or discretization error can be decreased by increasing the discretization resolution or the sampling frequency.
(A) Digital signal processing and control. Analog or continuous experimental data measured are sampled or discretized at discrete time points (analog-digital conversion) and processed to generate digital control signals, which are transformed into analog signals through digital-to-analog conversion. (B) Simple two-gene network. First, xgene is transcribed into xmRNA, which is then translated into xprotein. In the presence of signal sx, xprotein transforms into its active form x*protein and binds to the promoter of ygene, transcribing ygene into ymRNA. As ymRNA is translated, yprotein is produced. The effect of yprotein production by xprotein can be counteracted by two processes that decrease yprotein concentration: degradation (protein destruction) and dilution (concentration reduction due to increased cell volume).
Proteins are the worker molecules of biological systems. They perform virtually every activity within living organisms, including metabolism, cell division, apoptosis (programmed cell death), cell-cell interaction, etc. Therefore, it is not surprising that the biological information that each gene encodes is mainly for producing a specific type of protein. However, only knowing how a gene modulates its protein production is often insufficient to fully capture protein dynamics. A gene can activate or suppress the activity of other genes. This coupling or interaction of genes is called gene networks and any protein dynamics should to be understood in this context. It was suggested that gene networks are made of a small set of recurring modules called network motifs6,7.
Network motifs include simple two-gene network, autoregulation, feedforward loop and feedback loop. The complexity of gene networks originates not only from various interconnection patterns or the number of genes involved but also from their adaptive and robust features8,9,10,11,12,13,14. Although understanding these features is important to study the controllability of complex gene networks and to eventually control them15, a mathematical framework is not yet well-established. It is an on-going research topic not only for biology but also for other related fields, such as adaptive sensor networks and swarm robotics, which involve complex network dynamics9,16,17,18.
The overall aim of this article is to introduce digital signal processing and control as a useful tool for the study of gene networks. Since digital signal processing and control, not to mention gene networks, is a very broad field that encompasses a wide range of topics, it is impossible to systematically probe every topic in depth. Therefore, a sequence of topics and examples are presented in a way that motivates the readers to pursue them further. Every attempt was made to make the materials accessible not only to engineers, mathematicians, or physicists but also to life scientists, introducing the basics of both digital signal processing and control and gene networks.
Results
Simple two-gene network
Modeling simple two-gene network as a difference equation becomes important since it can serve as the basic building block for constructing more complex gene networks11. One gene (ygene) can be activated by another gene (xgene), as indicated by the notation x → y in Fig. 1B. This simple notation, however, involves multiple steps. First, xgene is transcribed into xmRNA, which is then translated into xprotein. In the presence of signal sx, xprotein transforms into its active form x*protein and binds to the promoter of ygene, transcribing ygene into ymRNA. As ymRNA is translated, yprotein is produced. Since protein activity is generally governed by concentration, we will express xprotein and yprotein in terms of concentration. The effect of yprotein production by xprotein can be counteracted by two processes that decrease yprotein concentration: degradation (protein destruction) and dilution (concentration reduction due to increased cell volume).
First, let us assume that yprotein is only degraded or diluted. There is no yprotein production by x*protein. This can be modeled using a difference equation:

where n is the discrete time index (integer) and y(n) is the concentration of yprotein at time n. Having a sufficiently small time interval between measurements is important to capture desired dynamics in detail (Nyquist sampling theorem1). In case we measure yprotein and x*proteinevery minute, the time difference between y(1) and y(2) is 1 minute. py can be any value between 0 and 1. It cannot be greater than 1, which makes yprotein increase, or less than 0, which makes yprotein negative. In case y(1) = 10 μM and py = 0.9:

which shows yprotein is indeed decreasing over time. The simulation code for Eq. 1 can be found online (see learnsysbio.net Module 119). If we lower py from 0.9 to 0.1:

which indicates yprotein is more rapidly decreasing. In other words, a smaller py value corresponds to greater degradation or dilution.
Next, let us add a new term pxy x(n − 1) to Eq. 1 to model yprotein production by x*protein:

where n is the discrete time index (integer) and y(n) is the concentration of yprotein at time n and x(n) is the concentration of x*proteinat time n. Note the value y(n) at time n now depends on the previous values y(n−1) and x(n −1) at time n - 1. The parameter pxyshows how strongly x*protein activating ygene. pxycan be affected by many factors, including the presence of signal sx, transcription factor/promoter binding strength, etc. It cannot be indefinitely large since yprotein production is restricted by the finite amount of available protein production machineries such as ribosomes.
An example with constant x(n) values (=10 μM), y(1) = 0 μM, py = 0.9 and pxy = 0.2, can be shown as:

The simulation code for Eq. 5 can be found online (see learnsysbio.net Module 219) and the simulation result is shown in Fig. 2A. From Eq. 5, following expressions can be derived:
(A) The simulation result of Eq. 4. yprotein reaches a constant or steady-state level as time approaches infinity while yprotein production and degradation and/or dilution are simultaneously occurring. (B) The time constant τ (tau) represents the time it takes yprotein to reach approximately 63.2% of the steady-state level. It is also called the response time, which can be used to evaluate how fast yprotein changes or responds to the input signals. (C) The effect of different pxy values on yprotein. As pxy increases, the steady-state level also increases because x*proteinis increasingly activating ygene. However, the time constant τ does not change, indicating that pxy, which governs yproteinproduction, does not affect how fast yprotein reaches its steady-state level. (D) The effect of different py values on yprotein. As py decreases (degradation increases), the steady-state level decreases because yprotein is degraded or diluted more. Note the time constant τ also decreases, which means yprotein reaches its steady-state level faster as py decreases.

Eq. 6 shows that as time approaches infinity (N ≈ ∞) yprotein reaches a steady-state level given that py < 1 and pxyand xprotein values are not indefinitely large. This steady-state level is achieved while yprotein production and degradation and/or dilution are simultaneously occurring. The time constant τ (tau) represents the time it takes yprotein to reach 1 −1/e or approximately 63.2% of the steady-state level (Fig. 2B). It is also called the response time, which can be used to evaluate how fast yprotein changes or responds to the input signals.
Protein production and degradation exhibit different dynamics
Figure 2C shows the effect of different pxy values on yprotein. As pxy increases, the steady-state level also increases because x*proteinis increasingly activating ygene. However, the time constant τ does not change, indicating that pxy, which governs yproteinproduction, does not affect how fast yprotein reaches its steady-state level (see learnsysbio.net Module 319). Figure 2D shows the effect of different py values on yprotein. As py decreases (degradation increases), the steady-state level decreases because yprotein is degraded or diluted more. Note the time constant τ also diminishes, which means yprotein reaches its steady-state level faster as py decreases (see learnsysbio.net Module 419). In summary, protein production affects only steady-state level, while protein degradation can affect both steady-state level and response time. This difference can be used to achieve target steady-state level with desired response time as shown in Fig. 3. Figure 3A shows a particular target steady-state level (approximately 15 μM) can be achieved with pxy = 0.15 and py = 0.9. The response time is about 10 minutes. Decreasing pyfrom 0.9 to 0.4 (increasing protein degradation) reduces the response time to approximately 2 minutes, which is desired (Fig. 3B). However, the steady-state level is also substantially reduced as a side effect. How can we achieve the target steady-state level of 15 μM with the response time of 2 minutes ? Figure 3C shows this can be done by increasing pxy from 0.15 (Fig. 3A) to 0.9 while maintaining low py (high protein degradation). In other words, we can achieve the target steady-state level with desired response time by co-modulating protein production (pxy) and degradation (py).
Achieving target steady-state level with desired response time.
(A) A target steady-state level (approximately 15 μM) is achieved with pxy = 0.15 and py = 0.9. The response time is about 10 minutes. (B) Decreasing pyfrom 0.9 to 0.4 (increasing protein degradation) reduces the response time to approximately 2 minutes, which is desired. However, the steady-state level is also substantially reduced as a side effect. (C) The target steady-state level of 15 μM with the response time of 2 minutes can be achieved by increasing pxy from 0.15 to 0.9 while maintaining low py (high protein degradation).
Protein production and degradation are also “asymmetric”. Protein production is a slow process compared to protein degradation and this asymmetry can be exploited to generate various protein dynamics. An example is illustrated in Fig. 4. Let us assume cells want to change protein level from Level 1 to Level 2 by increasing its production as shown in Fig. 4A. Since protein production is a slow process, increasing its rate is also slow. Note degradation is low in both Level 1 and Level 2. Cells can also achieve Level 1 with high production and high degradation as shown in Fig. 4B. In this case, Level 2 can be reached by lowering degradation. Since production is already at high speed, the transition from Level 1 and Level 2 occurs faster. Using this co-modulation in various ways, cells may generate pulses with desired frequency, amplitude and duration (Fig. 4C,D), which has biological significance in DNA repair, tumorigenesis, embryonic development, etc.20,21,22.
Co-modulating protein production and degradation (and/or dilution).
(A) By increasing protein production from low to high, a transition can occur from Level 1 to Level 2. Note degradation is low in both Level 1 and Level 2. (B) Level 1 can also be achieved with high production and high degradation. In this case, lowering degradation enables a faster transition from Level 1 to Level 2. (C) Protein pulses with high (blue) and low (brown) frequencies. High-frequency protein pulses (blue) show short pulse duration while low-frequency protein pulses (brown) show longer pulse duration. (D) Protein pulses with high (blue) and low (brown) amplitudes.
Robustness of steady-state level
The first term of Eq. 6, which depends on y(1) or the initial value of yprotein, becomes zero as time goes to infinity, indicating that the steady-state level does not depend on the initial value. For example, if we change y(1) from 0 to 5 μM, the steady-state level will not be affected (see Fig. 5A and learnsysbio.net Module 519). Furthermore, steady-state level can be robustly maintained while automatically restoring its value in the presence of disturbance (see Fig. 5B and learnsysbio.net Module 619). The yprotein dynamics defined by Eq. 4 enables this robustness of steady-state level.
Matrix representation of simple two-gene network
Matrix computation is widely used in computational science and engineering23 and representing gene network dynamics using matrices and vectors can be useful. From Eq. 4, following expressions can be derived:

These expressions can be compactly represented using matrices and vectors:

Given A and x we can find y, which becomes solving a system of linear equations.
Basal and saturated production
yprotein can be produced without being activated by other genes, which is called basal production. This production does not depend on x*proteinand can be denoted as b0:

When simulating gene networks, basal production can be added to the model to prevent protein levels from becoming negative. yprotein cannot indefinitely increase as x*proteinincreases because yprotein production eventually becomes saturated due to limited availability of protein synthesis resources (e.g., ribosomes). This can be modeled as:

where ymaxis the maximum level yprotein can be. We will use Eq. 4, which does not consider basal and saturated production, for simplicity in this article.
Stochastic modeling: extrinsic and intrinsic noise
Biological processes including gene expression are inherently stochastic constantly affected by noise24,25,26. Different types of noise influencing gene expression include extrinsic and intrinsic noise24. Extrinsic noise is “global” and universally affects the expression of all genes in a given cell. It is generated by factors such as variations in the number of RNA polymerase, ribosome, etc. In contrast, intrinsic noise is “local” and caused by noise propagated from upstream genes to downstream genes. It is generated by the randomness inherent in gene expression and has been used to analyze gene regulatory links27. In our simple two-gene network model, xgene (upstream gene) activates ygene (downstream gene), which means extrinsic noise affecting xgene gene expression can be propagated to create intrinsic noise in ygene gene expression. This is demonstrated in Fig. 6. Initially, there is no noise affecting xprotein and yprotein levels (Fig. 6A). Extrinsic noise obeying the normal (Gaussian) distribution (mean: 0, standard deviation: 1) is only added to xprotein (see Fig. 6B and learnsysbio.net Module 719). Although no noise is added to yprotein, fluctuations in yprotein levels (intrinsic noise) are observed, which is caused by extrinsic noise propagated from xprotein to yprotein. Interestingly, yprotein fluctuations are much less than xprotein fluctuations because our simple two-gene network is a low-pass filter, which removes or reduces high-frequency noise signals. This will be further discussed later. When extrinsic noise is added to yprotein as well, yprotein fluctuations look similar to xprotein fluctuations (see Fig. 6C and learnsysbio.net Module 819).
Extrinsic and intrinsic noise.
(A) There is no noise affecting xprotein and yprotein levels. (B) Extrinsic or global noise obeying a normal distribution (mean: 0, standard deviation: 1) is added to xprotein only. Although no noise is added to yprotein, fluctuations in yprotein levels are observed, which is intrinsic noise caused by extrinsic noise propagated from xprotein to yprotein. (C) Extrinsic noise is added to yprotein.
Predicting yprotein levels
When measured xprotein and yprotein data (e.g., Fig. 6C) are available, the parameter values pxy and py of Eq. 4 can be estimated, which can be used for predicting unknown yprotein level. There are mainly two models we can use for this prediction: 1) time-invariant models with fixed parameter values and 2) time-variant models with parameter values changing adaptively over time. Gene networks are often treated as time-invariant by computational models but it was previously demonstrated that adaptive time-variant models approximate experimental measurements more accurately than time-invariant models, while reducing modeling complexity and representing gene network dynamics more realistically10. Before proceeding any further, Eq. 4 can be modified into a more general form:

where y(n) at time n depends not only on immediate previous values x(n −1) and y(n −1) but also on other older x and y values (e.g., x(n −3) and y(n −5)). There are M previous x terms and N previous y terms determining the current value of y(n). The parameters a1, …, aM and b1, …, bN show how each previous x and y term affects y(n). In case the values of these parameters are fixed, Eq. 11 represents a time-invariant model. In contrast, an adaptive time-variant model allows them to change over time. Let us first examine a time-invariant model with fixed parameter values. The parameters or weights can be compactly represented by a single column vector w:

where superscript T stands for transpose, which changes a row vector into a column vector. The data vector d can be defined as:

For example, in case we define our model as:

w and d can be expressed as:

Using Eqs 12 and 13, Eq. 11 can be compactly expressed as:

Assuming wopt is the parameter vector computed in an optimal way:

where and  is the estimated value of y(n), which can be measured experimentally. The difference or error between y(n) and
is the estimated value of y(n), which can be measured experimentally. The difference or error between y(n) and  can be denoted as e(n):
can be denoted as e(n):

One approach for finding wopt is using the Least Squares (LS) estimation method such that ∑e(n)2 is minimized4,10:

where wLS is wopt computed by the method. Applying Eq. 19 to our previous example model (Equations 14 and 15), we get:

Once wLS is found,  can be predicted using Eq. 17:
can be predicted using Eq. 17:

Figure 7A shows an example of yprotein prediction using the least squares approach. Simulated data similar to Fig. 6C are used. As discussed previously by the author10, the estimation performance using this approach is generally poor due to highly “time-varying” nature of gene expression even if we increase the model complexity by adding more terms to Eq. 14.
yprotein level prediction using the Wiener filter
There is another approach for yprotein prediction using a time-invariant model called the Wiener filter28. The Wiener filter computes wopt that minimizes the expected value of e(n)2. The concepts of random variable, discrete-time random process and correlation will be briefly reviewed before they are discussed29. Let us assume that we measure y[n] using fluorescent reporter technology30. y(82), the yprotein level at time 82 (n = 82), is called a random variable whose value can randomly change in each experiment. A collection of these random variables (e.g., y(1), y(2), y(3), …) at discrete time points is called a discrete-time random process. The expected value of random variable y(n) can be defined as:

where k is the number of values y(n) can take. In theory, we need an infinite number of experiment results to find the exact expected value of a random variable. The autocovariance function, which shows how two random variables that belong to the same (“auto”) random process “co-vary”, can be defined as:

where n1 and n2 can be any time point from the identical discrete-time random process y(n). The first term of Eq. 23 is the autocorrelation function:

The cross-covariance function, which shows how two random variables that belong to two different (“cross”) random processes “co-vary”, can be defined as:

where x is a discrete-time random process formed by random variables x(1), x(2), x(3), …. The first term of Eq. 25 represents the cross-correlation function:

The Weiner filter can be used to estimate the parameters shown in Eq. 12 using autocorrelation and cross-correlation:

where the correlation matrix R is E[d(n)d(n)T] and the correlation vector p is  is wopt computed by the Wiener filter. Once wWF is found, it can be used to predict
is wopt computed by the Wiener filter. Once wWF is found, it can be used to predict  (Eq. 17):
(Eq. 17):

Although the Weiner filter can perform better than the Least Squares method (Eq. 19), it is based on the assumption that x and y are wide-sense stationary random processes and may not perform well if x and y are non-stationary random processes28,29. Furthermore, finding expected values requires a substantial number of prior experiments to be performed, which is often not possible. Most of all, the approach assumes that the parameter values to be estimated are fixed and do not change over time. However, biological systems are highly dynamic and it is possible that those values will constantly change, demanding tracking of such fluctuating parameter values. Adaptive filters address these issues.
yprotein level prediction using adaptive filters
Adaptive filters iteratively update wopt(n) that attempts to minimize e(n)2. The Least Means Squares (LMS) filter achieves this using the stochastic gradient descent method31:

where wLMS(n) is wopt(n) computed using LMS at time n and μ is the step size, which can be tuned to optimize performance. Let us use LMS to estimate the time-varying parameter values of simple two-gene network model shown in Eq. 4 (a1 = pxy and b1 = py):

 and d(n) can be defined as:
and d(n) can be defined as:


Note wLMS(n) is not fixed and can constantly change over time. Using Eqs 31 and 32,  can be compactly expressed as:
can be compactly expressed as:

The difference or error between measured  and estimated
and estimated  can be denoted as
can be denoted as  :
:

Using Eqs 31 and 32, Eq. 29 can be re-expressed as:


Since  is known,
is known,  can be computed:
can be computed:

Once measured y(n) is available, wLMS(n + 1) can be computed, which is then used to estimate  and these steps are repeated. An example of LMS-enabled yprotein level estimation is shown in Fig. 7B (also see learnsysbio.net Module 919). Note the estimation error e(n) is large in the beginning but soon substantially reduced as the filter “learns” adaptively over time. Taking time variation into consideration allows low-order simple models (e.g., Eq. 30, Fig. 7B) to outperform more complex higher-order, time-invariant models (e.g., Eq. 14, Fig. 7A)10. Although adaptive filtering is introduced as an estimation technique for better fitting a model to data, the same approach can be used to elucidate the adaptive behavior of biological systems9,13,14. Another possible extension of this work is to use adaptive filters and various forms of control mechanisms, such as adaptive control methods, for identifying and controlling the stochastic dynamics of gene networks in real time as described later.
and these steps are repeated. An example of LMS-enabled yprotein level estimation is shown in Fig. 7B (also see learnsysbio.net Module 919). Note the estimation error e(n) is large in the beginning but soon substantially reduced as the filter “learns” adaptively over time. Taking time variation into consideration allows low-order simple models (e.g., Eq. 30, Fig. 7B) to outperform more complex higher-order, time-invariant models (e.g., Eq. 14, Fig. 7A)10. Although adaptive filtering is introduced as an estimation technique for better fitting a model to data, the same approach can be used to elucidate the adaptive behavior of biological systems9,13,14. Another possible extension of this work is to use adaptive filters and various forms of control mechanisms, such as adaptive control methods, for identifying and controlling the stochastic dynamics of gene networks in real time as described later.
Simple two-gene network is a low-pass filter
Any discrete-time signal (time-domain) can be decomposed into a collection of sine or cosine waves with different amplitudes, frequencies and phases (frequency domain) (Fig. 8A). Using the z-transform, Eq. 4 can be converted into its frequency domain representation2:
(A) Any discrete-time signal (time-domain) can be decomposed into a collection of sine or cosine waves with different amplitudes, frequencies and phases (frequency domain). (B) The frequency response of H(z) can be illustrated using Bode plot. The effect of extrinsic noise signals added to xprotein levels with cycle period shorter than 30 min (high-frequency noise) will be reduced in yprotein expression, indicating Eq. 4 is a low-pass filter that passes low-frequency xprotein signals while attenuating high-frequency xprotein signals.

where  ,
,  and z is a complex number. When performing the z-transform, the region of convergence, which is the set of points in the complex plane for which the z-transform summation converges, needs to be considered. H(z) is called the transfer function, which represents the system and transforms input X(z) into output Y(z). The frequency response of H(z) can be illustrated using Bode plot as shown in Fig. 8B (pxy = 0.2, py = 0.9). The effect of extrinsic noise signals added to xprotein levels with cycle period shorter than 30 min (high-frequency noise) will be reduced in yprotein expression (Fig. 6B), indicating Eq. 4 is a low-pass filter that passes low-frequency xprotein signals while attenuating high-frequency xprotein signals. This way, cells can prevent unwanted noise signals from propagating from upstream genes to downstream genes. It is intriguing that this filtering mechanism is achieved by co-modulating protein production (pxy) and degradation (py). Eq. 4 is also called an Infinite Impulse Response (IIR) filter in digital signal processing1. The response is “infinite” because there is feedback (y(n −1) → y(n)) in the filter.
and z is a complex number. When performing the z-transform, the region of convergence, which is the set of points in the complex plane for which the z-transform summation converges, needs to be considered. H(z) is called the transfer function, which represents the system and transforms input X(z) into output Y(z). The frequency response of H(z) can be illustrated using Bode plot as shown in Fig. 8B (pxy = 0.2, py = 0.9). The effect of extrinsic noise signals added to xprotein levels with cycle period shorter than 30 min (high-frequency noise) will be reduced in yprotein expression (Fig. 6B), indicating Eq. 4 is a low-pass filter that passes low-frequency xprotein signals while attenuating high-frequency xprotein signals. This way, cells can prevent unwanted noise signals from propagating from upstream genes to downstream genes. It is intriguing that this filtering mechanism is achieved by co-modulating protein production (pxy) and degradation (py). Eq. 4 is also called an Infinite Impulse Response (IIR) filter in digital signal processing1. The response is “infinite” because there is feedback (y(n −1) → y(n)) in the filter.
The discrete Fourier transform (DFT) is a special form of the z-transform widely used in science and engineering (frequency analysis, fast convolution, image processing, etc.) because it can mathematically reveal periodicities (frequency components) in discrete-time data as well as the relative strengths of any frequency components32. For example, let us assume fluorescence intensity values of xprotein measured four times (the time-interval: 1 minute) are 2, 0, 4 and 7:

The DFT of the time series data x(n) can be computed using:

where ω(m) is angular frequency in radian per minute. 2π radian corresponds to one full cycle. For example, 4π radian per minute is equivalent to 2 cycles per minute. Since the total number of time-domain data N is 4, m can also take 4 different integer values, which generates 4 different ω(m) and X(ω(m)) values:
m = 0 (0 rad/min or 0 cycle/min):

m = 1 (0.5π rad/min or 0.25 cycle/min):

m = 2 (π rad/min or 0.5 cycle/min):

m = 3 (1.5π rad/min or 0.75 cycle/min):

The magnitude of each complex number X(ω(m)) informs the relative strength of each frequency component, i.e., how much it contributes to the formation of x(n):

The result of DFT is “mirrored” meaning that the values of  for 0 ≤ ω(m) ≤ π are equivalent to those of
for 0 ≤ ω(m) ≤ π are equivalent to those of  for π ≤ ω(m) ≤ 2π. In this respect, we can disregard the result for m = 3 (1.5π rad/min), which is equivalent to the result for m = 1 (0.5π rad/min). It was reported p53, one of the most studied genes in cancer biology, forms a negative feedback loop with MDM2 and p53 protein levels oscillate upon DNA damage by γ-irradiation33. Figure 9A shows such p53 oscillation. Note that there are about five cycles per 30 hours or 0.18 cycles per hour. By letting x(n) represent the p53 protein levels,
for π ≤ ω(m) ≤ 2π. In this respect, we can disregard the result for m = 3 (1.5π rad/min), which is equivalent to the result for m = 1 (0.5π rad/min). It was reported p53, one of the most studied genes in cancer biology, forms a negative feedback loop with MDM2 and p53 protein levels oscillate upon DNA damage by γ-irradiation33. Figure 9A shows such p53 oscillation. Note that there are about five cycles per 30 hours or 0.18 cycles per hour. By letting x(n) represent the p53 protein levels,  can be computed using Eq. 39 (Fig. 9B)34. It is shown that the frequency component 0.18 cycle/hour has high
can be computed using Eq. 39 (Fig. 9B)34. It is shown that the frequency component 0.18 cycle/hour has high  value represented by a tall peak, indicating that it is one of the prominent frequency components contributing to x(n).
value represented by a tall peak, indicating that it is one of the prominent frequency components contributing to x(n).
p53 oscillation.
(A) There are about five cycles per 30 hours or 0.18 cycles per hour. (B) By letting x(n) represent the p53 protein levels,  can be computed using Eq. 39. It is shown that the frequency component (0.18 cycle/hour) has high
can be computed using Eq. 39. It is shown that the frequency component (0.18 cycle/hour) has high  value represented by a tall peak, indicating that it is one of the prominent frequency components contributing to x(n).
value represented by a tall peak, indicating that it is one of the prominent frequency components contributing to x(n).
Autoregulation
Positive autoregulation (PAR) occurs when a gene promotes its own protein production (positive feedback, Fig. 10A). The equation for PAR can be obtained by adding an additional term, which represents positive autoregulation, to Eq. 4 (see learnsysbio.net Module 1019).

or

where par is the positive autoregulation parameter (par > 0). PAR increases the response time, the steady state value and cell-cell variation in protein levels8. Negative autoregulation (NAR) occurs when a gene represses its own gene expression (negative feedback, Fig. 10B). The equation for NAR can be obtained by adding an extra term, which represents negative autoregulation, to Eq. 4 (see learnsysbio.net Module 1019).

or

where nar is the negative autoregulation parameter (nar > 0). It is shown that NAR can decrease the response time and the steady state value, while reducing cell-cell variation in protein levels8.
Feedforward loop
Coherent type-1 feedforward loop (C1-FFL) and incoherent type-1 feedforward loop (Ic1-FFL) are commonly found FFLs in biological systems7. It was reported that C1-FFL causes delay in gene expression while Ic1-FFL induces pulse-like transient gene expression. C1-FFL can be expressed using following equations (Fig. 10C):

where three genes x, y and z form C1-FFL, which induces delay in z (see learnsysbio.net Module 1119). Ic1-FFL can be expressed using following equations (Fig. 10D):

where three genes x, y and z form Ic1-FFL, which induces pulse-like transient z gene expression (see learnsysbio.net Module 1219). C1-FFLs and Ic1-FFLs can be combined into more complex and larger gene networks. An example called interlocked FFL can be found in Bacillus subtilis, which generates sequential expression of multiple genes required for differentiation (see Fig. 10E and learnsysbio.net Module 1319,35).

Negative feedback control of protein levels
Gene networks are continuously affected by noise or fluctuations. Nevertheless, it is remarkable that they can robustly perform their functions in the presence of such disturbances. Feedback control theory informs us that feedback, a situation in which two (or more) dynamical sub-systems are connected in a way that their dynamics are coupled, can make a system resilient towards disturbances36. Feedback control theory can be used 1) to study the inherent robust feature of natural gene networks and 2) to manipulate the dynamics of genetically-modified gene networks with man-created control inputs. The main goal of the first approach is to gain insights, which may be experimentally validated using the second approach. For example, the author previously suggested that the p53-Mdm2 negative feedback gene network robustly achieves low levels of p5311. Since p53 protein may trigger apoptosis or “programmed cell death” when its levels are high, robustly maintaining them low using Mdm2 as a “negative feedback controller” becomes biologically significant. Although it is beyond the scope of this article, probing the uncertainty of gene network models, which may include various types of unmodeled dynamics (nonlinearity, etc.), is an important research topic36,37.
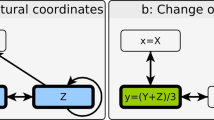
Equation 37 can be represented by the block diagram shown in Fig. 11A. X(z) is the input, Y(z) is the output and H(z) is the transfer or system function that processes the input to produce the output. Since the system may have other inputs than X(z) we can redefine H(z) as Hy(z) such that it includes only py, which is independent of X(z) (Fig. 11B). When designed properly, a negative feedback loop can reduce the impact of unwanted inputs or disturbances that influence the output of a system38. When a system receives desired input signal in the presence of unwanted input or disturbance (Fig. 11C), the output is affected by both inputs. The effect of such disturbance on the output can be reduced by adding a negative feedback loop and a controller to the system (Fig. 11D). The same mechanism can be used to reduce the disturbance effect on yprotein levels (Fig. 11E,F). A new controller gene “c” is added to the gene network, which forms a negative feedback loop with y (Fig. 11F). Discrete-time difference equations for this model can be expressed as:
(A) Block diagram representation of Eq. 37. X(z) is the input, Y(z) is the output and H(z) is the transfer or system function that processes the input to produce the output. (B) Since the system may have other inputs than X(z) we can redefine H(z) as Hy(z) such that it includes only py, which is independent of X(z). (C) When a system receives desired input signal in the presence of unwanted input or disturbance, the output is affected by both inputs. (D) The effect of such disturbance on the output can be reduced by adding a negative feedback loop and a controller to the system. (E,F) The same mechanism shown in D can be used to reduce of the disturbance effect on yprotein levels. (G) Block diagram representation of Eqs 47 and 48. (H) Steady-state error (the difference or error between target and actual steady-state levels as time goes to infinity) depends on disturbance.


where all the parameter values are positive (see learnsysbio.net Module 1419). The negative sign for y(n − 1) term in Eq. 48 indicates that y is downregulating c (negative feedback).
Steady-state error analysis
Steady-state error (the difference or error between target and actual steady-state levels as time goes to infinity) depends on disturbance, which can be analyzed mathematically2,11. Using the z-tranform, Eqs 47 and 48 can be represented by the block diagram shown in Fig. 11G. E(z) is the difference or error between pxc X(z) and pyc Y(z), which needs to be minimized and distrubance is denoted as D(z). E(z) can be expressed as11:

From the block diagram, Y(z) can also be written as:

Substituting Y(z) in Eq. 50 by Eq. 49:

The second term in Eq. 51 represents the effect of D(z) on E(z) or the effect of the disturbance on the error, which needs to be minimized. This term can be denoted by ED(z) and its corresponding time domain discrete-time signal as eD(n). Using the final value theorem and assuming a step disturbance for D(z) (=z/(z − 1)), we can compute the steady-state error due to the disturbance as follows (Fig. 11H):

Interestingly, Eq. 52 provides insight that the steady-state error caused by the disturbance can be reduced when pcy is increased or py is decreased11. In other words, how fast protein molecules are produced (pcy) and degraded (py) can have an effect on the robustness of gene networks, although they may seem irrelevant.
Stability analysis
Substituting E(z) in Eq. 50 by Eq. 49 and assuming no disturbance (D(z) = 0):


Complex numbers p1 and p2, which makes the denominator of H(z) zero, are called the poles of the transfer function. If the poles lie within the unit circle on the complex plane (the magnitude of each pole (complex number) is less than or equal to one), the system is stable and the output does not blow up2. From Eq. 11, a general form for H(z) can be derived:

Again, the stability of this system can be analyzed by finding the poles and checking if they lie within the unit circle on the complex plane.
Stability analysis using state-space representation
Equation 47 and 48 can be compactly represented by matrices and vectors:

where  is the state vector,
is the state vector,  is the state matrix,
is the state matrix,  is the input matrix and
is the input matrix and  is the input vector. This is called state-space representation and the eigenvalues of the state matrix are equivalent to the pole values of transfer function shown in Eq. 53. If the magnitude of each eigenvalue is less than or equal to one, the system is stable.
is the input vector. This is called state-space representation and the eigenvalues of the state matrix are equivalent to the pole values of transfer function shown in Eq. 53. If the magnitude of each eigenvalue is less than or equal to one, the system is stable.
In silico digital control of protein levels
As mentioned earlier, man-created control inputs can be used to manipulate the dynamics of genetically-modified gene networks, which may validate insights gained through mathematical modeling. One way of artificially modulating protein dynamics is using optogenetics, which was originally developed for modulating genetically modified light-sensitive ion channels in neurons39. For example, it was recently demonstrated that intracellular protein levels can be controlled using light by modulating protein production40,41 and degradation42 (Fig. 12A). Targeted time-varying protein levels in living cells are achieved using real-time fluorescent reporter image processing and in silico feedback control. Co-modulating protein production and degradation, harnessing the strengths of each mechanism, may generate protein dynamics previously shown in Fig. 4. Protein dynamics control virtually all cellular processes, including metabolism, growth, cell division, intercellular communication, etc., therefore, the capability of generating desired protein levels in individual cells can be immensely useful for unraveling the mechanism of these processes.
(A) Intracellular protein levels can be controlled using light by modulating protein production and degradation. Targeted time-varying protein levels in living cells are achieved using real-time fluorescent reporter imaging and in silico feedback control. (B) Desired or “reference” fluorescence intensity at time n is denoted as r(n). e(n) is the difference or “error” between r(n) and measured fluorescence intensity value x(n) at time n. Upon receiving error signal e(n), the controller uses this error and a control algorithm, such as the PID (proportional-integral-derivative) control, to compute control signal c(n), which is the intensity of light given to the cell.
Figure 12B illustrates an in silico digital control scheme, which can be used to modulate protein levels using light. Desired or “reference” fluorescence intensity at time n is denoted as r(n). e(n) is the difference or “error” between r(n) and measured fluorescence intensity value x(n) at time n:

Upon receiving the error signal e(n), a control algorithm, such as the PID (proportional-integral-derivative) control, may generate a control signal c(n). It is the intensity of light given to the cell to minimize e(n). For example, c(n) generated by a PID controller can be expressed as:

where KP, KI and KD are the controller parameters, which can be tuned for optimized performance and stability. Two types of c(n) signals can be used in parallel to co-modulate x(n) levels since protein production and degradation should rely on different colors of light to minimize cross-talk. Gene expression and relevant protein dynamics are slow processes, which take minutes and hours and not seconds and the time interval between control input signals is typically greater than a minute40,41.
Real-time parameter estimation using adaptive filters described previously can be used for system identification, which may lead to better performance. For this, a simple mathematical model similar to Eq. 4 can be formulated as:

Note measured fluorescence intensity value x(n) at time n depends on two previous values at time n −1, x(n −1) and control signal c(n −1). Once pcx and px are adaptively estimated, a set of PID controller parameters (KP, KI and KD), which achieves desired performance and robustness, can be computed and updated in real time43. It is also possible to address model (parameter) uncertainty based on adaptively estimated parameter values and to design a controller using model predictive and robust control theory (robust adaptive control), although it is beyond the scope of this article44.
Discussion
In this article, it was proposed digital signal processing and control provides useful tools for the study of gene networks. It was shown that discrete-time difference equations can be used to study complex dynamics of gene networks by incorporating time and frequency domain approaches. Most importantly, it was suggested that digital signal processing and control algorithms can be used not only to model, simulate and analyze gene networks but also to interact with them in real time since the experimental environment is mostly digital today. By no means this article is comprehensive and many digital signal processing and control concepts and tools (e.g., band-pass filter, etc.), which can be useful for the study of gene networks, were not discussed and will be addressed in future studies.
Methods
MATLAB (Mathworks, USA) and JavaScript programming language were used for simulation. The source code for online modules (learnsysbio.net) is available on GitHub45.
Additional Information
How to cite this article: Shin, Y.-J. Digital Signal Processing and Control for the Study of Gene Networks. Sci. Rep. 6, 24733; doi: 10.1038/srep24733 (2016).
References
Proakis, J. G. & Manolakis, D. G. Digital signal processing: principles, algorithms and applications (Prentice Hall, 1996).
Franklin, G. F. & Powell, J. D. Digital control of dynamic systems (Addison-Wesley, 1980).
Karlebach, G. & Shamir, R. Modelling and analysis of gene regulatory networks. Nature Reviews Molecular Cell Biology 9, 770–780 (2008).
Strang, G. Linear algebra and its applications (Thomson Learning, 2006).
Hamming, R. W. Numerical methods for scientists and engineers (Dover, 1986).
Milo, R. et al. Network motifs: simple building blocks of complex networks. Science 298, 824–827 (2002).
Alon, U. Network motifs: theory and experimental approaches. Nat. Rev. Genet. 8, 450–461 (2007).
Shin, Y. & Bleris, L. Linear control theory for gene network modeling. PLOS ONE 5, e12785 (2010).
Shin, Y., Sayed, A. H. & Shen, X. Using an adaptive gene network model for self-organizing multicellular behavior (Conf. Proc. IEEE Eng. Med. Biol. Soc., 5249–5263, 2012).
Shin, Y., Sayed, A. H. & Shen, X. Adaptive models for gene networks. PLOS ONE 7, e31657 (2012).
Shin, Y., Chen, K., Sayed, A. Hencey, B. & Shen, X. Post-translational regulation enables robust p53 regulation. BMC Systems Biology 7, 83–83 (2013).
Chandra, F. A., Buzi, G. & Doyle, J. C. Glycolytic oscillations and limits on robust efficiency. Science 333, 187–192 (2011).
Cattivelli, F. S. & Sayed, A. H. Modeling Bird Flight Formations Using Diffusion Adaptation. IEEE Transactions on Signal Processing, 59, 2038–2051 (2011).
Li, J., Tu, S.-Y. & Sayed, A.H. Honeybee swarming behavior using diffusion adaptation (Digital Signal Processing Workshop and IEEE Signal Processing Education Workshop (DSP/SPE), 249–254, 2011).
Liu, Y., Slotine, J. & Barabási, A. Controllability of complex networks. Nature 473, 167 (2011).
Xavier, J. B. Social interaction in synthetic and natural microbial communities. Mol. Syst. Biol. 7, 483 (2011).
Tu, S. Y. & Sayed, A. H. Mobile adaptive networks. IEEE Journal on Selected Topics in Signal Processing 5, 649–664 (2011).
Brambilla, M., Ferrante, E., Birattari, M. & Dorigo, M. Swarm robotics: a review from the swarm engineering perspective. Swarm Intell 7, 1–41 (2013).
Shin, Y. Learn Systems Biology. http://learnsysbio.net (2016) Date of access: 02/23/2016.
Loewer, A., Batchelor, E., Gaglia, G. & Lahav, G. Basal Dynamics of p53 Reveal Transcriptionally Attenuated Pulses in Cycling Cells. Cell 142, 89–100 (2010).
Novak, K. Tumorigenesis: Clockwork. Nature Reviews Cancer 2, 810 (2002).
Aulehla, A. & Pourquié, O. Oscillating signaling pathways during embryonic development. Curr. Opin. Cell Biol. 20, 632–637 (2008).
Golub, G. H. Matrix computations (ed Van Loan, C. F. ) (Johns Hopkins University Press, 1989).
Elowitz, M. B., Levine, A. J., Siggia, E. D. & Swain, P. S. Stochastic gene expression in a single cell. Science 297, 1183–1186 (2002).
Kaern, M., Elston, T. C., Blake, W. J. & Collins, J. J. Stochasticity in gene expression: from theories to phenotypes. Nat. Rev. Genet. 6, 451–464 (2005).
Raj, A. & van Oudenaarden, A. Nature, nurture, or chance: stochastic gene expression and its consequences. Cell 135, 216–226 (2008).
Dunlop, M. J., Cox, R. S., 3rd., Levine, J. H., Murray, R. M. & Elowitz, M. B. Regulatory activity revealed by dynamic correlations in gene expression noise. Nat. Genet. 40, 1493–1498 (2008).
Kay, S. M. Fundamentals of statistical signal processing (Prentice-Hall, 1993).
Fotopoulos, S. B. Probability and Random Processes. Technometrics 49, 365–365 (2007).
Nathan, C. S., Paul, A. S. & Roger, Y. T. A guide to choosing fluorescent proteins. Nature Methods 2, 905 (2005).
Sayed, A. H. Adaptive Filters (Wiley-IEEE Press, 2008).
Oppenheim, A. V. & Schafer, R. W. Discrete-time signal processing (Pearson, 2010).
Geva-Zatorsky, N. et al. Oscillations and variability in the p53 system. Mol. Syst. Biol. 2, 2006.0033 (2006).
Geva-Zatorsky, N., Dekel, E., Batchelor, E., Lahav, G. & Alon, U. Fourier analysis and systems identification of the p53 feedback loop. Proc. Natl. Acad. Sci. USA 107, 13550–13555 (2010).
Eichenberger, P. et al. The program of gene transcription for a single differentiating cell type during sporulation in Bacillus subtilis. PLoS Biol. 2, e328 (2004).
Doyle, J. C., Francis, B. A. & Tannenbaum, A. Feedback control theory (Macmillan, 1992).
Zhou, K. & Doyle, J. C. Essentials of robust control (Prentice Hall, 1998).
Nise, N. S. Control systems engineering (Wiley, 1994).
Fenno, L., Yizhar, O. & Deisseroth, K. The development and application of optogenetics. Annu. Rev. Neurosci. 34, 389 (2011).
Melendez, J. et al. Real-time optogenetic control of intracellular protein concentration in microbial cell cultures. Integrative Biology 6, 366–372 (2014).
Milias-Argeitis, A. et al. In silico feedback for in vivo regulation of a gene expression circuit. Nat. Biotechnol. 29, 1114–1116 (2011).
Renicke, C., Schuster, D., Usherenko, S., Essen, L. & Taxis, C. A LOV2 Domain- Based Optogenetic Tool to Control Protein Degradation and Cellular Function (Report). Chem. Biol. 20, 619 (2013).
Atherton, D. P. Autotuning of PID Controllers: Relay Feedback Approach. Int. J. Adapt. Control. Signal. Process. 14, 559–562 (2000).
Petros, I. & Jing, S. Robust adaptive Control (Dover, 2012)
Shin, Y. Learn Systems Biology GitHub Repository. https://github.com/yshin1209/learnsysbio (2016) Date of access: 02/23/2016.
Author information
Authors and Affiliations
Contributions
Y.-J.S. wrote the main manuscript text and prepared the figures.
Ethics declarations
Competing interests
The author declares no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Shin, YJ. Digital Signal Processing and Control for the Study of Gene Networks. Sci Rep 6, 24733 (2016). https://doi.org/10.1038/srep24733
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep24733
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.