Abstract
It has been proposed that adding disorder to a topologically trivial mercury telluride/cadmium telluride (HgTe/CdTe) quantum well can induce a transition to a topologically nontrivial state. The resulting state was termed topological Anderson insulator and was found in computer simulations of the Bernevig-Hughes-Zhang model. Here, we show that the topological Anderson insulator is a more universal phenomenon and also appears in the Kane-Mele model of topological insulators on a honeycomb lattice. We numerically investigate the interplay of the relevant parameters and establish the parameter range in which the topological Anderson insulator exists. A staggered sublattice potential turns out to be a necessary condition for the transition to the topological Anderson insulator. For weak enough disorder, a calculation based on the lowest-order Born approximation reproduces quantitatively the numerical data. Our results thus considerably increase the number of candidate materials for the topological Anderson insulator phase.
Similar content being viewed by others
Introduction
Topological insulators (TIs) are novel materials which have raised a great deal of interest over the past decade1,2. One of their distinguishing features is the existence of conducting boundary states together with an insulating bulk. The boundary states are protected by time-reversal symmetry (TRS) and exist both in two-dimensional (2D) and three-dimensional (3D) TIs. In 2D TIs, the boundary states lead to an edge conductance of one conductance quantum per edge for chemical potentials inside the bulk band gap3,4,5.
It is a challenging task to find candidate materials for TIs. So far, only a limited number of materials are known. The most prominent 2D TIs are HgTe/(Hg, Cd)Te quantum wells (HgTeQWs)6 and InAs/GaSb heterostructures7,8, whereas 3D TIs were found for instance in Bi1−xSbx9. The fact that their metallic surface states emerge due to a topological property of the bulk band structure means that they are robust to weak disorder. However, one expects that a large amount of disorder should ultimately localize the surface states and render them insulating.
All the more surprising, it was predicted that the opposite transition can happen in certain parameter ranges: adding strong disorder can convert a trivial insulator without edge states into a topological insulator with perfectly conducting edge states. Materials that exhibit this new state have been termed topological Anderson insulators (TAIs).
This effect was first theoretically predicted based on the lattice version of the Bernevig-Hughes-Zhang (BHZ) model for HgTeQWs in the presence of Anderson disorder10,11. For Anderson disorder, a random on-site potential, uniformly distributed in an energy window of width 2W, is assigned to each lattice site of a tight-binding model. From Anderson’s theory of localization12 one expects that a system with finite conductance without disorder undergoes a transition to a system with localized states and suppressed conductance as the disorder is increased beyond a certain threshold value. The behavior of TAIs instead is quite different. A TAI is an ordinary band insulator in the clean limit. Above a critical disorder strength W, an interesting topological state appears, in which the material features a quantized conductance. For even stronger W, above the disorder strength at which the states of the conduction and valence band localize, it was proposed that tunneling across the bulk becomes possible13, probably enabled by percolating states14 and the conductance is again suppressed.
The disorder-induced transition can be understood by a renormalization of the model parameters. The BHZ model with disorder and band mass m can be approximated by an effective model of a clean system and renormalized mass  . Using an effective-medium theory and the self-consistent Born approximation (SCBA), it was shown that for certain model parameters,
. Using an effective-medium theory and the self-consistent Born approximation (SCBA), it was shown that for certain model parameters,  can become negative even if the bare mass m is positive15. As a consequence, the effective model becomes that of a TI and features edge states with a quantized conductance of G0 = e2/h16.
can become negative even if the bare mass m is positive15. As a consequence, the effective model becomes that of a TI and features edge states with a quantized conductance of G0 = e2/h16.
Furthermore, TAIs have been predicted in several related systems, for instance in a honeycomb lattice described by the time-reversal-symmetry breaking Haldane model17, a modified Dirac model17, the BHZ model with sz non-conserving spin-orbit coupling18, as well as in 3D topological insulators19. Moreover, similar transitions from a topologically trivial to a topologically nontrivial phase have been found to be generated by periodically varying potentials20 or phonons21. In contrast to on-site Anderson disorder, certain kinds of bond disorder cannot produce a TAI as they lead only to a positive correction to m22,23. So far, however, the TAI phase was not found in the Kane-Mele model on a honeycomb lattice, describing for example graphene or proposed TIs such as silicene, germanene and stanene24,25,26,27. First indications to this phase were already found, showing that the Kane-Mele model without a staggered sublattice potential hosts extended bulk states even for large disorder strengths28.
In this paper we show the existence of TAIs in the Kane-Mele model by means of tight-binding calculations. The interplay between the parameters characterizing intrinsic spin-orbit coupling (SOC) λSO, extrinsic Rashba SOC λR and a staggered sublattice potential λν turns out to be crucial for the visibility of TAIs and we calculate the parameter ranges in which TAIs can be observed. We find analytically that to lowest order in W, the parameters λSO and λR are not renormalized with increasing disorder strength, in contrast to λν. However, a new effective hopping λR3 is generated due to the disorder, which is related but not identical to λR. Although λR is not a crucial ingredient for the existence of TAIs, it significantly alters the physics of topological insulators in various ways29,30 and, as we will show below, strongly affects the TAI state.
Even though recently first signs of a TAI phase may have been found experimentally in evanescently coupled waveguides31, there has been no experimental evidence so far for the existence of the TAI phase in fermionic systems. The main difficulty is the requirement of a rather large and specific amount of disorder, which is difficult to control in the topological insulators currently investigated, where the 2D TI layer is buried inside a semiconductor structure. In contrast, producing and controlling disorder in 2D materials described by the Kane-Mele model could be much easier. Disorder in 2D materials with honeycomb structure can be produced by randomly placed adatoms32,33 or a judicious choice of substrate material34,35,36,37. Moreover, a sizeable staggered sublattice potential can be generated via a suitable substrate material38. Other means of engineering disorder were proposed in periodically driven systems39,40. Finally, honeycomb structures with the SOC necessary to produce a topological phase have already been realized using ultracold atoms in optical lattices41, in which disorder can in principle be engineered.
Results
Setup
The basis of our calculations is the Kane-Mele model5 given by the following Hamiltonian on a tight-binding honeycomb lattice

which has been supplemented by an on-site Anderson disorder term with disorder strength W and uniformly distributed random variables  . The summations over the lattice sites 〈ij〉 and 〈〈i, j〉〉 include all nearest neighbors and next-nearest neighbors, respectively. The operators
. The summations over the lattice sites 〈ij〉 and 〈〈i, j〉〉 include all nearest neighbors and next-nearest neighbors, respectively. The operators  ,
,  are creation and annihilation operators for the site i of the lattice. The parameters t, λSO and λR are the nearest-neighbor hopping strength, intrinsic SOC and Rashba SOC, respectively. If the next-nearest neighbor hopping from site j to site i corresponds to a right-turn on the honeycomb lattice, then νij = 1, otherwise νij = −1. Furthermore, s =(sx, sy, sz) is the vector of Pauli matrices for the spin degree of freedom and
are creation and annihilation operators for the site i of the lattice. The parameters t, λSO and λR are the nearest-neighbor hopping strength, intrinsic SOC and Rashba SOC, respectively. If the next-nearest neighbor hopping from site j to site i corresponds to a right-turn on the honeycomb lattice, then νij = 1, otherwise νij = −1. Furthermore, s =(sx, sy, sz) is the vector of Pauli matrices for the spin degree of freedom and  is the unit vector between sites j and i. The Wannier states at the two basis atoms of the honeycomb lattice are separated in energy by twice the staggered sublattice potential λν, with ξi = 1 for the A sublattice and ξi = −1 for the B sublattice. The lattice constant is a.
is the unit vector between sites j and i. The Wannier states at the two basis atoms of the honeycomb lattice are separated in energy by twice the staggered sublattice potential λν, with ξi = 1 for the A sublattice and ξi = −1 for the B sublattice. The lattice constant is a.
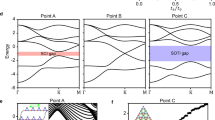
The band structure of this model depends strongly on the parameter set λSO, λR and λν. In the clean limit and for λR = 0, the system will be a topological insulator for  and a trivial insulator otherwise5. The tight-binding lattice and examples for the band structure in the clean limit are displayed in Fig. 1. For W = λν = 0, the system will be a topological insulator if
and a trivial insulator otherwise5. The tight-binding lattice and examples for the band structure in the clean limit are displayed in Fig. 1. For W = λν = 0, the system will be a topological insulator if  and a metal or semimetal otherwise. For finite λν and λR the situation is more complex and a topological transition appears for values within these two boundaries.
and a metal or semimetal otherwise. For finite λν and λR the situation is more complex and a topological transition appears for values within these two boundaries.
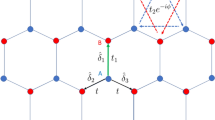
(a) Toy model illustrating the tight-binding terms in the Kane-Mele Hamiltonian (1). The blue color scale marks different on-site potentials. Thick black lines correspond to nearest-neighbor hopping and Rashba SOC, while thin green lines correspond to intrinsic SOC. The leads attached at both sides (red color) are modeled by a hexagonal lattice with nearest-neighbor hopping term and finite chemical potential. In this example, the sample has width w = 5a and length l = 6a. Much larger sample sizes of w = 93a and length l = 150a were used in the calculations described below. (b) Band structures of infinitely long samples of width w = 93a for two different values of λν showing a topologically nontrivial and a trivial gap. Vertical and horizontal axis correspond to energy in units of t and dimensionless momentum, respectively. Parameters are λSO = 0.3t and λR = 0.
Numerical solution
For λR = 0, we find a TAI phase for parameters close to the topological transition at  . Changing this ratio corresponds to changing the band mass in the case of the BHZ model. Figure 2 shows the conductance for different values of λν. We find that for
. Changing this ratio corresponds to changing the band mass in the case of the BHZ model. Figure 2 shows the conductance for different values of λν. We find that for  the system is a topological insulator. For W = 0, i.e., in the clean case, the conduction and valence bands are separated by a red region with a quantized conductance of 2G0. Remarkably, with increasing disorder strength, the states in the conduction and valence bands localize, but the helical edge states that are responsible for the conductance of 2G0 exist for an even larger energy window. The conductances and the vanishing error bars for the two distinct energy values EF = 0, EF = 0.2t in the lower row of Fig. 2 show that the conductance quantization and with it the topological nature of the system, persist for the vast majority of microscopic disorder configurations. Interestingly, for λν = 1.65t = 5.5λSO, the system is a trivial insulator at W = 0. The trivial gap closes however and at W ≈ t the system develops a topologically non-trivial gap and edge states. This can be seen from the quantized conductance. Finally, for λν = 1.85t ≈ 6.2λSO, the closing of the trivial gap and re-opening of the topological gap happens at a disorder strength which is strong enough to destabilize the emergent topological phase. Features of the conductance quantization can still be seen, but this behavior is not that robust anymore. As no averaging is done in the upper row of Fig. 2 and a new disorder configuration is taken for every data point, destabilization of the topological phase can be seen by red and white speckles in the figure.
the system is a topological insulator. For W = 0, i.e., in the clean case, the conduction and valence bands are separated by a red region with a quantized conductance of 2G0. Remarkably, with increasing disorder strength, the states in the conduction and valence bands localize, but the helical edge states that are responsible for the conductance of 2G0 exist for an even larger energy window. The conductances and the vanishing error bars for the two distinct energy values EF = 0, EF = 0.2t in the lower row of Fig. 2 show that the conductance quantization and with it the topological nature of the system, persist for the vast majority of microscopic disorder configurations. Interestingly, for λν = 1.65t = 5.5λSO, the system is a trivial insulator at W = 0. The trivial gap closes however and at W ≈ t the system develops a topologically non-trivial gap and edge states. This can be seen from the quantized conductance. Finally, for λν = 1.85t ≈ 6.2λSO, the closing of the trivial gap and re-opening of the topological gap happens at a disorder strength which is strong enough to destabilize the emergent topological phase. Features of the conductance quantization can still be seen, but this behavior is not that robust anymore. As no averaging is done in the upper row of Fig. 2 and a new disorder configuration is taken for every data point, destabilization of the topological phase can be seen by red and white speckles in the figure.
Top row: The conductance from the left to the right lead as a function of the disorder strength W (horizontal axis) and chemical potential EF (vertical axis).
The conductance varies from 0 (white) to 30G0 (dark blue). The quantized value of 2G0 (red for all conductances within [1.95G0, 2.05G0]) originates from two helical edge states. The three plots show the conductance for three different values of λν that represent, respectively, a topological insulator, a TAI and a TAI at the transition to an ordinary insulator. The black lines are obtained from a lowest-order Born approximation without any adjustable parameter. The two dotted lines mark the energies EF = 0, EF = 0.2t. Bottom row: The conductance at fixed chemical potentials EF = 0 (black) and EF = 0.2t (red) for the same parameters as in the top row. The errors bars originate from an averaging procedure over 100 disorder configurations. The vanishing error bars in the regions with a conductance of 2G0 show that the topological phase is stable irrespective of the exact disorder configuration. The system parameters are w = 93a, l = 150a, λSO = 0.3t and λR = 0.
We find that no TAI exists without staggered sublattice potential (λν = 0). If both λν and λR are finite, the TAI phase is in general less pronounced, see Fig. 3. The plot on the right shows the closing of a trivial gap and emergence of a topological phase at W ≈ 0.5t.
The conductance for increasing disorder strength W and chemical potentials EF for three different values of λR = 0 (left), λR = 0.5t (middle) and λR = 0.65t (right).
The system parameters are w = 93a, l = 150a, λSO = 0.3t and λν = 0.95t. The black lines are obtained from a lowest-order Born approximation without any fitting parameter. The conductance color code is the same as in Fig. 2.
Furthermore, we observe that the simultaneous presence of intrinsic and Rashba SOC (both λR ≠ 0 and λSO ≠ 0) destroys the particle-hole symmetry in the spectrum. In the absence of Rashba SOC, the symmetry operator ϒ, which acts on the lattice operators as  and
and  for the sublattices A and B, leaves the (disorder-free) Hamiltonian invariant. ϒ can be viewed as particle-hole conjugation combined with spatial inversion and the inversion is needed to leave the staggered sublattice potential term invariant.
for the sublattices A and B, leaves the (disorder-free) Hamiltonian invariant. ϒ can be viewed as particle-hole conjugation combined with spatial inversion and the inversion is needed to leave the staggered sublattice potential term invariant.
Lowest-order Born approximation
In the self-consistent Born approximation, the self-energy ∑ for a finite disorder strength is given by the following integral equation15,42

where  is the Fourier transform of H in the clean limit5. The coefficient 1/3 originates from the second moment
is the Fourier transform of H in the clean limit5. The coefficient 1/3 originates from the second moment  of the uniform distribution function of the disorder amplitudes and EF is the chemical potential. The integration is over the full first Brillouin zone. We use the lowest-order Born approximation, which means setting ∑ = 0 on the right-hand side of the equation.
of the uniform distribution function of the disorder amplitudes and EF is the chemical potential. The integration is over the full first Brillouin zone. We use the lowest-order Born approximation, which means setting ∑ = 0 on the right-hand side of the equation.
After a low-energy expansion of  , the integral can be evaluated analytically15 for λR = 0. This requires keeping the terms up to second order in k wherever this is the leading k-dependent order. The evaluation yields the renormalized staggered sublattice potential
, the integral can be evaluated analytically15 for λR = 0. This requires keeping the terms up to second order in k wherever this is the leading k-dependent order. The evaluation yields the renormalized staggered sublattice potential

For a certain set of parameters, the logarithm can be negative and  is reduced compared to λν. Moreover, we find that λSO is not renormalized to order W2. Therefore, it is possible to obtain
is reduced compared to λν. Moreover, we find that λSO is not renormalized to order W2. Therefore, it is possible to obtain  . The system thus makes a transition from a trivial insulator to a topological insulator with increasing W.
. The system thus makes a transition from a trivial insulator to a topological insulator with increasing W.
For a more quantitative treatment, we evaluate the integral for the full Hamiltonian  numerically. The self-energy ∑ is then written as a linear combination of several independent contributions
numerically. The self-energy ∑ is then written as a linear combination of several independent contributions

with  and Γab = [Γa, Γb]/(2i). Here, σx, σy, σz denote the Pauli matrices for the sublattice index. This leads to the following equations for the renormalized quantities
and Γab = [Γa, Γb]/(2i). Here, σx, σy, σz denote the Pauli matrices for the sublattice index. This leads to the following equations for the renormalized quantities

whereas  and
and  remain unrenormalized to lowest order in W. Surprisingly, a new coupling
remain unrenormalized to lowest order in W. Surprisingly, a new coupling  is created by the disorder. This coupling has the matrix structure Γ3, which is similar but not identical to the one for Rashba SOC. Expressing this new term in the lattice coordinates of Eq. (1) reveals that it corresponds to a Rashba-type nearest-neighbor hopping term which is asymmetric and appears only for bonds that are parallel to the unit vector (0, 1),
is created by the disorder. This coupling has the matrix structure Γ3, which is similar but not identical to the one for Rashba SOC. Expressing this new term in the lattice coordinates of Eq. (1) reveals that it corresponds to a Rashba-type nearest-neighbor hopping term which is asymmetric and appears only for bonds that are parallel to the unit vector (0, 1),

where 〈ij〉ν stands for summations over strictly vertical bonds only. Furthermore, we find to lowest order in W that  for λR = 0.
for λR = 0.
For W = λR = 0, the upper and lower edge of the gap are at the energies  . This is the case for both topological and trivial insulators. Extrapolation of these equations to finite W leads to the conditions
. This is the case for both topological and trivial insulators. Extrapolation of these equations to finite W leads to the conditions  . The solid black lines in Fig. 2 are the two solutions to these equations and describe the closing and reopening of the gap qualitatively for small W.
. The solid black lines in Fig. 2 are the two solutions to these equations and describe the closing and reopening of the gap qualitatively for small W.
For finite λR and therefore finite λR3, there is no analytical expression of the gap energy. In this case, we read off the positions of the gap edges from band structure calculations for several values of λR and λR3. An interpolation leads to two functions hU,L(λν, λR, λR3) for the upper and lower band edge in the clean system. Replacing the unperturbed by the renormalized parameters yields two equations

The solutions of these equations are indicated by the solid black lines in Fig. 3. Hence, these results agree with the numerical data for small W without any fitting parameter. Deviations appear for larger W, when the lowest-order Born approximation is not applicable.
Phase diagram
Figure 4 shows a phase diagram as a function of λν and λR based on the tight-binding simulations. The dark color marks the regions for which a critical disorder strength Wc exists above which the system is a TAI (blue for λSO = 0.3t, red for λSO = 0.15t). The TAI phase is located along the boundary separating trivial from topological insulators in the clean case. Towards larger λR, the TAI region becomes narrower and eventually vanishes above a critical λR. Figure 5 shows the critical disorder strength Wc as a function of λν for a fixed value of λR.
Phase diagram in the (λν, λR) plane.
Strong blue (red) color marks the region for which a TAI exists for λSO = 0.3t (0.15t). Transparent blue (red) color indicates the regions where a topological insulator is found for zero disorder. Each dot represents an individual simulation of the kind illustrated in Fig. 2.
In Figs 2 and 3 rather large values of the parameters λSO, λν and λR were chosen to better visualize the effect. The TAI phenomenon scales down also to smaller values of the parameters, as the red region in the Fig. 4 indicates, but the TAI phase becomes less pronounced in the conductance plots and is harder to identify. Material parameters for stanene for example are t = 1.3 eV, λSO = 0.1 eV43 and λR = 10 meV44. We suspect that disorder, e.g., originating from missing or dislocated atoms, can reach disorder strengths in the eV range.
Alternative disorder models
Anderson disorder is a special model for disorder which is not necessarily representative for all TI materials. To better understand the effect of the disorder model, we briefly remark on the following disorder Hamiltonian

In contrast to the Anderson disorder model, where a random potential is assigned to every lattice site, here the distribution function for ηi is such that only a fraction 0 < ρ ≤ 1 of the sites are affected by disorder. Denoting the total number of sites by N, we assume ηi = 1 on ρN/2 sites, ηi = −1 on ρN/2 sites and ηi = 0 on the remaining sites. The disorder amplitude W is constant. Because  , the normalization factor in Eq. (8) ensures that the mean squared disorder strength is equal to the Anderson disorder case for ρ = 1.
, the normalization factor in Eq. (8) ensures that the mean squared disorder strength is equal to the Anderson disorder case for ρ = 1.
For general ρ, the prefactor in Eq. (2) is thus replaced by ρW2/3. The lowest-order Born approximation for the disorder model (8) therefore predicts that a reduced disorder density ρ can be exactly compensated by an increased amplitude W. For large enough ρ, this is indeed confirmed in the tight-binding simulations.
However, because a single impurity (ρ = 1/N) cannot destroy the topological phase, it is clear that the TAI phase should eventually vanish for ρ → 0 at arbitrary W. Nevertheless, we find numerical evidence for the TAI phase at surprisingly low impurity densities. A TAI region remains pronounced for densities as low as ρ = 0.1.
Discussion
In conclusion, we have shown that the topological Anderson insulator is a significantly more universal phenomenon than previously thought. Using a combination of an analytical approach and tight-binding simulations, we have established that the topological Anderson insulator appears in the Kane-Mele model that describes potential topological insulators such as silicene, germanene and stanene and that can also be realized in optical lattices. We have observed a transition from a trivially insulating phase to a topological phase at a finite disorder strength and have mapped out the phase diagram as a function of the staggered sublattice potential (~λν) and the Rashba spin-orbit coupling (~λR). The new Anderson insulator exists at the boundary between trivial and topological insulators for small λR and finite λν, but not at the boundary between a semimetal and a topological insulator for small λν and finite λR. Since the Kane-Mele model on a honeycomb lattice describes a wide class of candidate materials for topological insulators, we hope that our work will trigger experimental efforts to confirm the existence of the topological Anderson insulator.
Methods
The numerical simulations were done with the tight-binding Hamiltonian (1) on a honeycomb lattice with rectangular shape of width w = 93a and length l = 150a using the Kwant code45. A smaller version of the sample is shown in Fig. 1. Both the upper and lower edge are taken to be of zigzag type. At the left and right edges two semi-infinite, metallic leads of width w are attached. The leads are also modeled by a honeycomb lattice with only nearest-neighbor hopping and a finite on-site energy of 1.2t to bring them into the metallic regime.
Additional Information
How to cite this article: Orth, C. P. et al. The topological Anderson insulator phase in the Kane-Mele model. Sci. Rep. 6, 24007; doi: 10.1038/srep24007 (2016).
References
Hasan, M. Z. & Kane, C. L. Colloquium: topological insulators. Rev. Mod. Phys. 82, 3045 (2010).
Qi, X. & Zhang, S. Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057 (2011).
Bernevig, B. A., Hughes, T. L. & Zhang, S.-C. Quantum spin Hall effect and topological phase transition in HgTe quantum wells. Science 314, 1757 (2006).
Kane, C. L. & Mele, E. J. Quantum spin Hall effect in graphene. Phys. Rev. Lett. 95, 226801 (2005).
Kane, C. L. & Mele, E. J. Z2 topological order and the quantum spin Hall effect. Phys. Rev. Lett. 95, 146802 (2005).
König, M. et al. Quantum spin Hall insulator state in HgTe quantum wells. Science 318, 766 (2007).
Knez, I., Du, R.-R. & Sullivan, G. Evidence for helical edge modes in inverted InAs/GaSb quantum wells. Phys. Rev. Lett. 107, 136603 (2011).
Li, T. et al. Observation of a helical Luttinger liquid in InAs/GaSb quantum spin Hall edges. Phys. Rev. Lett. 115, 136804 (2015).
Hsieh, D. et al. A topological Dirac insulator in a quantum spin Hall phase. Nature 452, 970 (2008).
Li, J., Chu, R.-L., Jain, J. K. & Shen, S.-Q. Topological Anderson insulator. Phys. Rev. Lett. 102, 136806 (2009).
Jiang, H., Wang, L., Sun, Q.-f. & Xie, X. C. Numerical study of the topological Anderson insulator in HgTe/CdTe quantum wells. Phys. Rev. B 80, 165316 (2009).
Anderson, P. W. Absence of diffusion in certain random lattices. Phys. Rev. 109, 1492 (1958).
Chen, L., Liu, Q., Lin, X., Zhang, X. & Jiang, X. Disorder dependence of helical edge states in HgTe/CdTe quantum wells. New J. Phys. 14, 043028 (2012).
Girschik, A., Libisch, F. & Rotter, S. Percolating states in the topological Anderson insulator. Phys. Rev. B 91, 214204 (2015).
Groth, C. W., Wimmer, M., Akhmerov, A. R., Tworzydło, J. & Beenakker, C. W. J. Theory of the topological Anderson insulator. Phys. Rev. Lett. 103, 196805 (2009).
Prodan, E. Three-dimensional phase diagram of disordered HgTe/CdTe quantum spin-Hall wells. Phys. Rev. B 83, 195119 (2011).
Xing, Y., Zhang, L. & Wang, J. Topological Anderson insulator phenomena. Phys. Rev. B 84, 035110 (2011).
Yamakage, A., Nomura, K. & Imura, K.-I., Kuramoto, Y. Disorder-Induced Multiple Transition Involving Z2 Topological Insulator. J. Phys. Soc. Jpn. 80, 053703 (2011).
Guo, H.-M., Rosenberg, G., Refael, G. & Franz, M. Topological Anderson insulator in three dimensions. Phys. Rev. Lett. 105, 216601 (2010).
Fu, B., Zheng, H., Li, Q., Shi, Q. & Yang, J. Topological phase transition driven by a spatially periodic potential. Phys. Rev. B 90, 214502 (2014).
Garate, I. Phonon-induced topological transitions and crossovers in Dirac materials. Phys. Rev. Lett. 110, 046402 (2013).
Song, J., Liu, H., Jiang, H., Sun, Q.-f. & Xie, X. C. Dependence of topological Anderson insulator on the type of disorder. Phys. Rev. B 85, 195125 (2012).
Lv, S.-H., Song, J. & Li, Y.-X. Topological Anderson insulator induced by inter-cell hopping disorder. J. Appl. Phys. 114, 183710 (2013).
Aufray, B. et al. Graphene-like silicon nanoribbons on Ag(110): A possible formation of silicene. Appl. Phys. Lett. 96, 183102 (2010).
Kara, A. et al. A review on silicene - new candidate for electronics. Surf. Sci. Rep. 67, 1 (2012).
Dvila, M. E., Xian, L., Cahangirov, S., Rubio, A. & Lay, G. L. Germanene: a novel two-dimensional germanium allotrope akin to graphene and silicene. New J. Phys. 16, 095002 (2014).
Zhu, F.-f. et al. Epitaxial growth of two-dimensional stanene. Nat. Mater. 14, 1020 (2015).
Prodan, E. Disordered topological insulators: a non-commutative geometry perspective. J. Phys. A: Math. Theor. 44, 113001 (2011).
Orth, C. P., Strübi, G. & Schmidt, T. L. Point contacts and localization in generic helical liquids. Phys. Rev. B 88, 165315 (2013).
Rod, A., Schmidt, T. L. & Rachel, S. Spin texture of generic helical edge states. Phys. Rev. B 91, 245112 (2015).
Stützer, S. et al. Experimental realization of a topological Anderson insulator. Paper presented at CLEO: QELS Fundamental Science 2015, San Jose (CA), United States, 10–15 May 2015, 10.1364/CLEO_QELS.2015.FTh3D.2.
Weeks, C., Hu, J., Alicea, J., Franz, M. & Wu, R. Engineering a robust quantum spin Hall state in graphene via adatom deposition. Phys. Rev. X 1, 021001 (2011).
Jiang, H., Qiao, Z., Liu, H., Shi, J. & Niu, Q. Stabilizing topological phases in graphene via random adsorption. Phys. Rev. Lett. 109, 116803 (2012).
Ando, T. Screening effect and impurity scattering in monolayer graphene. J. Phys. Soc. Jpn. 75, 074716 (2006).
Ishigami, M., Chen, J. H., Cullen, W. G., Fuhrer, M. S. & Williams, E. D. Atomic structure of graphene on SiO2 . Nano Letters 7, 1643–1648 (2007).
Fratini, S. & Guinea, F. Substrate-limited electron dynamics in graphene. Phys. Rev. B 77, 195415 (2008).
Varlet, A. et al. Tunable Fermi surface topology and Lifshitz transition in bilayer graphene. Synthetic Metals 210, 19 (2015) doi: 10.1016/j.synthmet.2015.07.006.
Nevius, M. S. et al. Semiconducting Graphene from Highly Ordered Substrate Interactions. Phys. Rev. Lett. 115, 136802 (2015).
Titum, P., Lindner, N. H., Rechtsman, M. C. & Refael, G. Disorder-induced Floquet topological insulators. Phys. Rev. Lett. 114, 056801 (2015).
Yang, Z. et al. Topological acoustics. Phys. Rev. Lett. 114, 114301 (2015).
Jotzu, G. et al. Experimental realization of the topological Haldane model with ultracold fermions. Nature 515, 237–240 (2014).
Bruus, H. & Flensberg, K. Many-Body Quantum Theory in Condensed Matter Physics (Oxford University Press, 2004).
Xu, Y. et al. Large-gap quantum spin Hall insulators in tin films. Phys. Rev. Lett. 111, 136804 (2013).
Liu, C.-C., Jiang, H. & Yao, Y. Low-energy effective Hamiltonian involving spin-orbit coupling in silicene and two-dimensional germanium and tin. Phys. Rev. B 84, 195430 (2011).
Groth, C. W., Wimmer, M., Akhmerov, A. R. & Waintal, X. Kwant: a software package for quantum transport. New J. Phys. 16, 063065 (2014).
Acknowledgements
C.P.O., T.S. and C.B. acknowledge financial support by the Swiss SNF and the NCCR Quantum Science and Technology. T.L.S. acknowledges support by National Research Fund, Luxembourg (ATTRACT 7556175).
Author information
Authors and Affiliations
Contributions
C.P.O. and T.S. performed the numerical simulations with input from C.B. and T.L.S. All authors contributed to writing the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Orth, C., Sekera, T., Bruder, C. et al. The topological Anderson insulator phase in the Kane-Mele model. Sci Rep 6, 24007 (2016). https://doi.org/10.1038/srep24007
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep24007
This article is cited by
-
Fredholm Homotopies for Strongly-Disordered 2D Insulators
Communications in Mathematical Physics (2023)
-
Observation of spin-polarized Anderson state around charge neutral point in graphene with Fe-clusters
Scientific Reports (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.