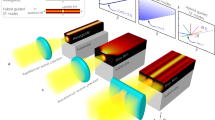
Abstract
Hybrid plasmonic (HP) modes allow strong optical field confinement and simultaneously low propagation loss, offering a potentially compact and efficient platform for on-chip photonic applications. However, their implementation is hampered by the low coupling efficiency between dielectric guided modes and HP modes, caused by mode mismatch and polarization difference. In this work, we present a mode-evolution-based polarization rotation and coupling structure that adiabatically rotates the TE mode in a silicon waveguide and couples it to the HP mode in a strip silicon-dielectric-metal waveguide. Simulation shows that high coupling factors of 92%, 78%, 75% and 73% are achievable using Ag, Au, Al and Cu as the metal cap, respectively, at a conversion length of about 5 μm. For an extremely broad wavelength range of 1300–1800 nm, the coupling factor is >64% with a Ag metal cap and the total back-reflection power, including all the mode reflections and backscattering, is below −40 dB, due to the adiabatic mode transition. Our device does not require high-resolution lithography and is tolerant to fabrication variations and imperfections. These attributes together make our device suitable for optical transport systems spanning all telecommunication bands.
Similar content being viewed by others
Introduction
Silicon (Si) photonics, which utilizes core and cladding materials that are compatible with complementary metal-oxide semiconductor (CMOS) technology for light guiding, modulation and detection, is promising for high-bandwidth communication and interconnection between computing nodes, due to the well-developed, low-cost CMOS manufacturing1,2,3,4,5. Further scaling down Si photonic devices for on-chip interconnects or information processing is hampered by, among others, the diffraction limit. Plasmonics in metallic nanostructures can confine light at subwavelength scale with enhanced field intensity6,7,8,9,10, thus in many cases breaking the diffraction limit and increasing the operating bandwidth11,12,13,14. The required power for an electro-optical modulation can also be reduced with increased light-matter interaction and reduced parasitic capacitance15. However, the use of plasmonic nanostructures is generally limited by the high optical loss in metals16,17.
Recently, hybrid plasmonic (HP) waveguide structures have been proposed to reduce the high propagation loss of plasmonic waveguides8,9. A typical HP waveguide consists of a Si core and a metal cap, in between which is a gap filled with a low-index material such as SiO2. When the gap is small, e.g. 50 nm, about 60% of the electromagnetic field can be confined within the low-index material, resulting in both a moderate propagation loss and a high field confinement in a low-index medium8,18. Electro-optical modulators15, nano-lasers10, ring-resonators19 and nonlinear optical devices20, based on, or related to HP waveguides have been demonstrated. Recently, various types of HP waveguide configurations based on nano-ridges21, metal ribbon buried slots22 and Si-on-nitride gap plasmon23 have been proposed at mid-infrared (MIR) to take advantage of the reduced propagation loss in plasmonic devices at these longer wavelengths, thus making HP waveguides attractive for MIR applications such as chemical and biological sensing24,25,26. To capitalize on these promising attributes of HP waveguides and integrate this platform into practical systems, meanwhile, requires a highly efficient and robust coupler between HP and Si waveguides to interface with Si photonics.
Previously, several schemes of couplers from Si waveguide to dielectric-loaded plasmonic waveguide27, metal-insulator-silicon-metal waveguide28 and HP waveguide29 have been proposed or demonstrated. Among them, the HP waveguide coupler design shows a broadband performance with a maximum coupling efficiency of about 70% at a gap size of 50 nm, from TM mode (electric field perpendicular to the surface) to HP mode29. However, in Si photonic devices, TE mode (electric field parallel to the surface) is dominant due to its higher confinement and ease of fabrication. Thus, to fully utilize the HP waveguide in Si photonic devices, it is essential to have an efficient coupler between TE mode and HP mode, that is, to rotate the TE mode in a Si waveguide and simultaneously couple the rotated mode to the HP mode. Achieving simultaneously high coupling efficiency (>90% with metal propagation loss), low reflection (<30 dB as on-chip isolators are not readily available), broad bandwidth (preferably > 500 nm to cover all telecommunication bands) and high tolerance to fabrication imperfections is highly desirable for such devices to be incorporated into large-scale silicon photonics integration and manufacturing. Unfortunately, to the best of our knowledge, no such couplers have been reported.
In purely dielectric photonic systems, mode-evolution based polarization splitter and rotators have been demonstrated with high performance30,31,32. Such devices usually include tapers to adiabatically splitting or rotating modes. However, simply tapering out the metal layer into sharp tips in a similar fashion does not achieve mode-evolution. Rather, the tapered sharp metal tip focuses and confines the light into the plasmonic mode33,34.
Several polarization rotators consisting of plasmonic structures have been proposed13,35 or fabricated14 to reduce the device length for Si photonic applications. Such devices utilize asymmetric HP structures, covering the top and one side-wall of Si waveguide with oxide and metal35 or tapering out the metal layer of HP waveguide13,14. However, these designs did not focus on the coupling to hybrid modes and are based on mode-coupling35 or a combination of mode-coupling and mode-evolution13,14. For example, in Fig. 2 of ref. 13, the oscillation in polarization extinction ratio (PER) from 2 μm to 7 μm for the case of 90 nm spacer thickness is a signature of mode-coupling. Therefore it remains interesting to find a scheme to achieve pure mode-evolution when plasmonic effect is involved and conduct a systematic investigation on the mechanism of transition between a dielectric mode and a HP mode.
In this paper, we present a truly mode-evolution-based polarization rotation and coupling (PRC) scheme that rotates the TE mode adiabatically and couples the rotated mode to the HP mode. When material absorption by metals is ignored, the coupler achieves almost 100% of efficiency with a proposed perfectly-phase-matched taper design. The performance of different metal caps (Cu, Au, Ag and Al) with a linear Si taper is evaluated and their spectral responses are assessed. Compared to mode-evolution structures in purely dielectric systems, our coupler has an upper limit of 92% efficiency when using silver as the metal cap, but it does have a much more compact size (~5 μm) and broader bandwidths (~500 nm), which are desirable in future dense optical integration.
Device design
Figure 1 shows the schematic view of the mode-evolution-based PRC structure and geometric parameters; w1 and w2 are the widths of Si waveguide at port 1 and HP waveguide at port 2, respectively and h1, h2 and h3 are the heights of Si core, SiO2 spacer and metal cap, respectively. The conversion/coupling region has a length of Lc and starts when the lateral shift between the metal cap and Si core is d and ends when the metal cap is exactly on top of the Si core. Through the conversion length Lc, the width of the Si core waveguide tapers from w1 to w2, while that of the metal cap is fixed to w2.
We first calculate and plot the effective refractive indices of each mode in Fig. 2 as a function of Si core width (w1 or w2). Finite element method (FEM) is used for the calculation with a free space wavelength of λ0 = 1550 nm. The refractive indices of Si and SiO2 are chosen to be nSi = 3.445 and  = 1.445. For the metal cap we choose Cu for its CMOS compatibility and the dispersive complex refractive index of Cu is used36. Waveguide heights are fixed to h1 = 220 nm, h2 = 30 nm and h3 = 100 nm. Here, the thickness of SiO2 spacer is chosen to strike a balance between the field confinement and propagation length for the subsequent hybrid mode8,9,18. In general, a small spacer thickness is desirable as it would lead to strong field confinement in the spacer, which is one of the motivations to incorporate hybrid modes into the silicon photonics platform8,9,18. A thinner spacer also requires an optimized coupler design as direct butt coupling would cause stronger reflection and scattering. Other thickness can also be selected to promote confinement over propagation loss or vice versa and the coupler can be designed accordingly. The thickness of Si core is chosen to be compatible with common silicon-on-insulator (SOI) wafers. TE01 (blue) and TM01 (green) are the fundamental TE and TM modes at port 1, respectively and HP02 (red) and TE02 (cyan) are the fundamental HP and TE modes at port 2, respectively. Our goal is to match the propagation constants (phases) between TE01 and HP02, while having a wide phase gap between TE01 and TE02. Here, we choose w2 = 300 nm and w1 = 405 nm as the port widths so that the phases of TE01 and HP02 modes are matched.
= 1.445. For the metal cap we choose Cu for its CMOS compatibility and the dispersive complex refractive index of Cu is used36. Waveguide heights are fixed to h1 = 220 nm, h2 = 30 nm and h3 = 100 nm. Here, the thickness of SiO2 spacer is chosen to strike a balance between the field confinement and propagation length for the subsequent hybrid mode8,9,18. In general, a small spacer thickness is desirable as it would lead to strong field confinement in the spacer, which is one of the motivations to incorporate hybrid modes into the silicon photonics platform8,9,18. A thinner spacer also requires an optimized coupler design as direct butt coupling would cause stronger reflection and scattering. Other thickness can also be selected to promote confinement over propagation loss or vice versa and the coupler can be designed accordingly. The thickness of Si core is chosen to be compatible with common silicon-on-insulator (SOI) wafers. TE01 (blue) and TM01 (green) are the fundamental TE and TM modes at port 1, respectively and HP02 (red) and TE02 (cyan) are the fundamental HP and TE modes at port 2, respectively. Our goal is to match the propagation constants (phases) between TE01 and HP02, while having a wide phase gap between TE01 and TE02. Here, we choose w2 = 300 nm and w1 = 405 nm as the port widths so that the phases of TE01 and HP02 modes are matched.
Figure 3(a) shows, from left to right, the normalized mode profiles (|E|) at the cross-sections of the device with the separation distance d = 600 nm, 200 nm and 0 nm, respectively and the corresponding Si core width w1 = 405 nm, 335 nm and 300 nm. Note that the case of d = 0 nm is the same as the cross-section of port 2 and d = 600 nm is the cross-section at the beginning of the conversion region. TE01 and SP01 are the TE and surface plasmon modes at the interface between port 1 and PRC, respectively and HP02 and TE02 are the HP and TE modes at port 2, respectively. PRCi is the i-th PRC mode in a hybrid state. Upper figures (TE01, PRC0 and HP02) are the main modes that play important roles in mode-evolution. This is an advantage over mode-coupling-based PRCs, where both PRC0 and PRC1 modes are excited for the rotation of polarization33,35.
(a) Normalized mode profiles (|E|) at the cross-sections of the PRC structure when the separation distance is changed from d = 600 nm (port 1) to d = 0 nm (port 2). (b) Effective refractive indices as a function of separation distance d and corresponding Si core width along the device. The main modes (TE01, PRC0 and HP02) and the secondary modes (SP01, PRC1 and TE02) are plotted in blue and dashed green, respectively.
To see the phase variations of mode-evolution in more detail, the effective refractive indices of main (blue line) and secondary (dashed green line) modes are plotted in Fig. 3(b) as a function of separation distance d and corresponding Si core width along the device. Notice that TE01 mode is adiabatically evolved into HP02 mode through PRC0 mode (blue line), while simultaneously maintaining a large phase gap to their secondary modes (dashed green line).
Results and Discussion
The performance of mode-evolution-based PRC with linear Si taper is evaluated by calculating the coupling factor to the HP mode (CFHP), which is defined as  , where
, where  is the input power of TE01 mode at port 1 and
is the input power of TE01 mode at port 1 and  is the output power of HP02 mode at port 2. 3D FEM simulations are conducted by exciting TE01 mode at port 1; then output fields of HP02 mode is decomposed to calculate the
is the output power of HP02 mode at port 2. 3D FEM simulations are conducted by exciting TE01 mode at port 1; then output fields of HP02 mode is decomposed to calculate the  33,37.
33,37.
Figure 4(a) shows the calculated CFHP of the linearly tapered PRC as a function of Lc, with different metal caps: Cu (blue), Au (green), Ag (red) and Al (cyan). Simulation results with the output port width w2 = 300 nm are plotted with plain lines and those with different port widths w2 − 20 nm and w2 + 20 nm are also presented with dotted and dashed lines, respectively. To show the designed PRCs are truly based on mode-evolution, Cu metal cap without metallic absorption loss is also evaluated (circled blue line) and its CFHP converges to about 97% after Lc = 5 μm. This is distinctively different from mode-coupling-based polarization rotation, which relies on the mode interference and the coupling factors show a sinusoidal oscillation as the conversion length increases13,14,33,35. In reality when metal absorption cannot be ignored, CFHP, decreases monotonously as the Lc increases, after reaching a maximum point. The trend for CFHP is similar with other metal caps, i.e.,  hits the maximum point then decreases as Lc increases; however, each metal cap shows different maximum point and descent rate. Especially, with a Ag cap, the maximum CFHP is ~92% and the descent rate is very slow, having over 80% of CFHP throughout the conversion lengths of 4 μm to 15 μm. Furthermore, simulations for w2 varied by ±20 nm show almost identical results for each material, suggesting that the devices are tolerant to fabrication variations. This is an another signature of the mode-evolution-based device and advantage over the mode-coupling-based one30,31. Also, the conversion lengths for the maximum CFHP are ultrashort with Lc ~ 5 μm. Typically, a mode-evolution-based device requires a long device length, e.g., hundreds of micrometers, to smoothly convert the mode adiabatically30,31; however, an ultrashort conversion length is achieved here, with a higher degree of field confinement in the HP mode
hits the maximum point then decreases as Lc increases; however, each metal cap shows different maximum point and descent rate. Especially, with a Ag cap, the maximum CFHP is ~92% and the descent rate is very slow, having over 80% of CFHP throughout the conversion lengths of 4 μm to 15 μm. Furthermore, simulations for w2 varied by ±20 nm show almost identical results for each material, suggesting that the devices are tolerant to fabrication variations. This is an another signature of the mode-evolution-based device and advantage over the mode-coupling-based one30,31. Also, the conversion lengths for the maximum CFHP are ultrashort with Lc ~ 5 μm. Typically, a mode-evolution-based device requires a long device length, e.g., hundreds of micrometers, to smoothly convert the mode adiabatically30,31; however, an ultrashort conversion length is achieved here, with a higher degree of field confinement in the HP mode
(a) Calculated CFHP of the linearly tapered PRC as a function of Lc with different metal caps: Cu (blue), Au (green), Ag (red) and Al (cyan). Circled blue line is the case of Cu without metallic loss. Simulation results with different port widths of w2 + 20 nm and w2 − 20 nm are also presented with dashed and dotted lines, respectively. (b) CFHP of the same devices as a function of λ0: Cu with Lc = 4.5 μm (blue), Au with Lc = 5.0 μm (green) and Ag with Lc = 5.5 μm (red). (c) Calculated back-reflection power R spectrum of the linearly tapered PRC with different mesh grid size: Δ = 5 nm (blue lines) and Δ = 3 nm (red lines). Solid lines are the total back-reflection power (Rtotal) and dashed lines are the TE component of the total back-reflection (RTE). Cu is used as the metal cap and the Lc = 4.5 μm.
In addition to high coupling efficiency, couplers need to have broad bandwidth to cover a wide range of operating wavelengths. The spectral responses of the linearly tapered PRC are shown in Fig. 4(b), for Cu (blue), Au (green) and Ag (red) metal caps. For each metal cap, different conversion lengths are chosen, which correspond to their maximum CFHP in Fig. 4(a): 4.5 μm, 5.0 μm and 5.5 μm for Cu, Au and Ag, respectively. Notice that, in every case, the spectral ranges with CFHP ≥ 50% are at least over 500 nm, covering the entire telecommunication bands.
In optical telecommunication systems, low back-reflection, or high return loss is also an important factor, especially for the emerging coherent transmission schemes. Despite recent advances38,39, on-chip optical isolators are not readily available, so a close-to-zero reflection is highly important if a device is to be considered for practical use. Figure 4(c) shows the calculated back reflection power of the linearly tapered PRC as a function of free space wavelengths. Cu is used as the metal cap and the device length is set to Lc = 4.5 μm. Solid lines are the total back-propagation power (Rtotal), accounting all possible reflections and scatterings. Dashed lines are the TE mode component of the total back-propagation (RTE). Simulations with two different mesh grid sizes (Δ) were included: Δ = 5 nm (blue lines) and Δ = 3 nm (red lines) and the results are almost identical, suggesting high likelihood of truthfulness. Overall the total back-propagating power is below −40 dB for the entire telecommunication wavelength range of 1300–1800 nm. Note that previous HP mode couplers showed about 2 ~ 4% of back-reflections29, but our mode-evolution based HP coupler shows an extremely low back-reflection, because our coupling mechanism is based on the mode-evolution, which allows an adiabatic and smooth mode transition.
Taper shape optimization
To further optimize the mode-evolution, the effective refractive indices of the main modes are calculated as functions of both w1 and d, while the other geometric parameters are fixed; then the index map is plotted in Fig. 5(a), again with Cu as the metal cap. The blue line on the figure is the case of linear tapering as in Fig. 3(b) and the green curved line delineate the contour of the Si waveguide taper whose main mode (PRC0) has the same effective refractive index as the HP02 mode. Note that the lower-right corner (d = 0 nm and w1 = 300 nm) is the point of pure HP02 mode and the end-points on top (w1 = 405 nm) are the points of pure TE01 mode. Keeping the separation distance d linearly, the Si waveguide core width w1 is tapered along the contour green line in Fig. 5(a); this tapering results in a perfect-phase-matching through the device. While there is a small phase deviation on PRC0 mode with a linear tapering (as the blue line in Fig. 3(b)), such deviation is removed with the contoured taper, which gives a perfect-phase-matching throughout the device. Figure 5(b) shows the calculated CFHP as a function of Lc for both tapers: blue lines for linear taper and green lines for perfectly-phase-matched (optimized) taper. Cases without considering the metal absorption are also plotted with dashed lines. Compared to linearly tapered design, perfectly-phase-matched tapering has shorter Lc for the maximum CFHP point and a little bit higher coupling factor for the case without metal absorption. The shorter Lc of perfectly-phase-matched tapering is due to the optimized separation distance d, making the effective interaction length longer. In terms of the coupling factor, even in the case without metal absorption, there is about 3% of loss with linear tapering (dashed blue line); this loss is due to the scattering that comes from the phase-mismatch and is removed by an optimized taper which gives the perfect phase-matching (dashed green line). After including absorption losses (thick lines), however, there is no appreciable improvement in coupling factor. This indicates that, in this mode-evolution-based PRC, the phase-mismatch is not a significant factor that determines the maximum coupling factor. Rather, as we’ve seen in Fig. 4(a,b), the metallic losses are the dominant factor that determines the maximum CFHP. The polarization conversion efficiency (PCE), which is defined as  , is also plotted in Fig. 5(c). Notice that the PCEs are almost 100% after Lc = 5 μm for every case. This shows that there are no remaining TE mode for these mode-evolution based PRCs after a short conversion length of merely Lc = 5 μm.
, is also plotted in Fig. 5(c). Notice that the PCEs are almost 100% after Lc = 5 μm for every case. This shows that there are no remaining TE mode for these mode-evolution based PRCs after a short conversion length of merely Lc = 5 μm.
(a) Effective refractive index map of the fundamental modes (TE01, PRC0, or HP02), as functions of separation distance d and Si core width w1. Blue and green lines are the cases of linear and optimized (perfectly-phase-matched) taperings, respectively. Calculated (b) CFHP and (c) PCE as a function of Lc for linear (blue) and optimized (green) taperings. Thick and dashed lines are the lossy and lossless cases, respectively.
Outline of device fabrication
In this section we describe briefly a potential route of fabrication for our proposed device. The fabrication can start from the deposition of a thin (e.g. 70 nm-thick) sacrificial silicon nitride (SiN) layer on top of the 220 nm-thick Si layer of a silicon-on-insulator (SOI) wafer. After the definition of Si waveguide via lithography and etching through the SiN and Si layers, a thick SiO2 layer will be deposited to cover the Si waveguides. Chemical mechanical polishing (CMP) can be applied to planarize the SiO2 top surface and the polishing will stop at the height of the top surface of the Si waveguide, using silicon nitride as the etch/polish stop. After removing the remaining SiN sacrificial layer, a 30 nm-thick layer of SiO2 can be deposited on the planarized surface with high precision in thickness to form the spacer between the Si and metal layers. The metal layers can be subsequently formed with lithography and lift-off to complete the fabrication of our device. To make the structure more robust, we propose to over clad the metal structures with SiO2 so that the metal is encapsulated between two SiO2 layers. The fabrication process does not require high-resolution lithography as all lateral features are above 300 nm, which can be achieved with any deep-UV projection lithography tools currently available in most CMOS manufacturing facilities.
Conclusion
In summary, we present a mode-evolution-based polarization rotation and coupling scheme that has a high coupling efficiency (the maximum CFHP is about 92% using Ag), an ultra-broad bandwidth (the spectral range with CFHP > 64% is over 500 nm) and near-zero reflection. Also, the device length is very short (Lc ~ 5 μm) and is tolerant to fabrication errors. The material property of plasmonic metal cap is important to the device performances such as the maximum coupling factor and the bandwidth. The Si waveguide core widths are also optimized with a perfect-phase-matching, reducing the conversion length and removing the scattering loss. This mode-evolution-based PRC scheme could meet the stringent requirements in optical communications systems and should be useful in HP-waveguide-based applications such as electro-optical modulators15, nano-lasers10, ring-resonators19, nonlinear optical devices20 and quantum plasmonic devices40,41,42.
Additional Information
How to cite this article: Kim, S. and Qi, M. Mode-evolution-based polarization rotation and coupling between silicon and hybrid plasmonic waveguides. Sci. Rep. 5, 18378; doi: 10.1038/srep18378 (2015).
References
Lipson, M. Guiding, modulating and emitting light on silicon-challenges and opportunities. J. Lightwave Technol. 23, 4222 (2005).
Kirchain, R. & Kimerling, L. A roadmap for nanophotonics. Nature Photon. 1, 303–305 (2007).
Soref, R. The past, present and future of silicon photonics. IEEE J. Sel. Topics Quantum Electron 12, 1678–1687 (2006).
Jalali, B. & Fathpour, S. Silicon photonics. J. Lightwave Technol. 24, 4600–4615 (2006).
Vlasov, Y. A., O’Boyle, M., Hamann, H. F. & McNab, S. J. Active control of slow light on a chip with photonic crystal waveguides. Nature 438, 65–69 (2005).
Sorger, V. J., Oulton, R. F., Ma, R.-M. & Zhang, X. Toward integrated plasmonic circuits. MRS bulletin 37, 728–738 (2012).
Brongersma, M. L. & Shalaev, V. M. Applied physics the case for plasmonics. Science 328, 440–441 (2010).
Alam, M. Z., Aitchison, J. S. & Mojahedi, M. A marriage of convenience: Hybridization of surface plasmon and dielectric waveguide modes. Laser Photon. Rev. 8, 394–408 (2014).
Oulton, R. F., Sorger, V. J., Genov, D., Pile, D. & Zhang, X. A hybrid plasmonic waveguide for subwavelength confinement and long-range propagation. Nature Photon. 2, 496–500 (2008).
Oulton, R. F. et al. Plasmon lasers at deep subwavelength scale. Nature 461, 629–632 (2009).
Guan, X., Wu, H., Shi, Y., Wosinski, L. & Dai, D. Ultracompact and broadband polarization beam splitter utilizing the evanescent coupling between a hybrid plasmonic waveguide and a silicon nanowire. Opt. Lett. 38, 3005–3008 (2013).
Kim, S. & Qi, M. Copper nanorod array assisted silicon waveguide polarization beam splitter. Opt. Express 22, 9508–9516 (2014).
Caspers, J. N., Alam, M. & Mojahedi, M. Compact hybrid plasmonic polarization rotator. Opt. Lett. 37, 4615–4617 (2012).
Caspers, J. N., Aitchison, J. S. & Mojahedi, M. Experimental demonstration of an integrated hybrid plasmonic polarization rotator. Opt. Lett. 38, 4054–4057 (2013).
Sorger, V. J., Lanzillotti-Kimura, N. D., Ma, R.-M. & Zhang, X. Ultra-compact silicon nanophotonic modulator with broadband response. Nanophotonics 1, 17–22 (2012).
Boltasseva, A. & Atwater, H. A. Low-loss plasmonic metamaterials. Science 331, 290–291 (2011).
West, P. R. et al. Searching for better plasmonic materials. Laser Photon. Rev. 4, 795–808 (2010).
Dai, D. & He, S. Low-loss hybrid plasmonic waveguide with double low-index nano-slots. Opt. Express 18, 17958–17966 (2010).
Ketzaki, D. A., Tsilipakos, O., Yioultsis, T. V. & Kriezis, E. E. Electromagnetically induced transparency with hybrid silicon-plasmonic traveling-wave resonators. J. Appl. Phys. 114, 113107 (2013).
Pitilakis, A. & Kriezis, E. E. Highly nonlinear hybrid silicon-plasmonic waveguides: analysis and optimization. J. Opt. Soc. Am. B 30, 1954–1965 (2013).
Mu, J. et al. Hybrid nano ridge plasmonic polaritons waveguides. Appl. Phys. Lett. 103, 131107 (2013).
Liang, H., Soref, R., Mu, J., Li, X. & Huang, W.-P. Long range mid-infrared propagation in si and ge hybrid plasmonic-photonic nano-ribbon waveguides. Opt. Express 22, 28489–28499 (2014).
Mu, J., Soref, R., Kimerling, L. C. & Michel, J. Silicon-on-nitride structures for mid-infrared gap-plasmon waveguiding. Appl. Phys. Lett. 104, 031115 (2014).
Soref, R. Mid-infrared photonics in silicon and germanium. Nature Photon. 4, 495–497 (2010).
Hu, J., Meyer, J., Richardson, K. & Shah, L. Feature issue introduction: mid-ir photonic materials. Opt. Mater. Express 3, 1571–1575 (2013).
Wang, J. et al. Monolithically integrated, resonant-cavity-enhanced dual-band mid-infrared photodetector on silicon. Appl. Phys. Lett. 100, 211106 (2012).
Briggs, R. M., Grandidier, J., Burgos, S. P., Feigenbaum, E. & Atwater, H. A. Efficient coupling between dielectric-loaded plasmonic and silicon photonic waveguides. Nano Lett. 10, 4851–4857 (2010).
Emboras, A. et al. Efficient coupler between silicon photonic and metal-insulator-silicon-metal plasmonic waveguides. Appl. Phys. Lett. 101, 251117–251117 (2012).
Song, Y., Wang, J., Li, Q., Yan, M. & Qiu, M. Broadband coupler between silicon waveguide and hybrid plasmonic waveguide. Opt. Express 18, 13173–13179 (2010).
Watts, M. & Haus, H. Integrated mode-evolution-based polarization rotators. Opt. Lett. 30, 138–140 (2005).
Watts, M., Haus, H. & Ippen, E. Integrated mode-evolution-based polarization splitter. Opt. Lett. 30, 967–969 (2005).
Watts, M. R. et al. Towards integrated polarization diversity: design, fabrication and characterization of integrated polarization splitters and rotators. In Optical Fiber Communication Conference, PDP11 (Optical Society of America, 2005).
Kim, S. & Qi, M. Polarization rotation and coupling between silicon waveguide and hybrid plasmonic waveguide. Opt. Express 23, 9968–9978 (2015).
Luo, Y. et al. On-chip hybrid photonic-plasmonic light concentrator for nanofocusing in an integrated silicon photonics platform. Nano Lett. 15, 849–856 (2015).
Jin, L., Chen, Q. & Wen, L. Mode-coupling polarization rotator based on plasmonic waveguide. Opt. Lett. 39, 2798–2801 (2014).
Johnson, P. B. & Christy, R.-W. Optical constants of the noble metals. Phys. Rev. B 6, 4370 (1972).
Yariv, A. & Yeh, P. Photonics: Optical Electronics in Modern Communications (Oxford University Press, Inc., 2006).
Fan, L. et al. An all-silicon passive optical diode. Science 335, 447–450 (2012).
Bi, L. et al. On-chip optical isolation in monolithically integrated non-reciprocal optical resonators. Nature Photon. 5, 758–762 (2011).
de Leon, N. P., Lukin, M. D. & Park, H. Quantum plasmonic circuits. IEEE J. Sel. Topics Quantum Electron. 18, 1781–1791 (2012).
Tame, M. et al. Quantum plasmonics. Nature Phys. 9, 329–340 (2013).
Fakonas, J. S., Lee, H., Kelaita, Y. A. & Atwater, H. A. Two-plasmon quantum interference. Nature Photon. 8, 317–320 (2014).
Acknowledgements
This work is supported in part by National Science Foundation grant CMMI-1120577, Defense Threat Reduction Agency grants HDTRA110-1-0106 and HDTRA1-07-C-0042, National Institute of Health grant 1R01RR026273-01, Air Force Office of Scientific Research grant FA9550- 12-1-0236 and DARPA PULSE program grant W31P40-13-1-0018 from AMRDEC.
Author information
Authors and Affiliations
Contributions
S.K. and M.Q. conceived the device design and wrote the manuscript. S.K. performed the numerical simulations.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Kim, S., Qi, M. Mode-evolution-based polarization rotation and coupling between silicon and hybrid plasmonic waveguides. Sci Rep 5, 18378 (2015). https://doi.org/10.1038/srep18378
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep18378
This article is cited by
-
Subwavelength silicon photonics for on-chip mode-manipulation
PhotoniX (2021)
-
Controlling evanescent waves using silicon photonic all-dielectric metamaterials for dense integration
Nature Communications (2018)
-
Ultracompact and high efficient silicon-based polarization splitter-rotator using a partially-etched subwavelength grating coupler
Scientific Reports (2016)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.