Abstract
Cylindrically polarized (CP) modes are laser beam modes which have rotational symmetry of the polarization distribution around the beam axis. Considerable attention has been paid to CP modes for their various applications. In this paper, by using the extended Stokes parameters and the degree of polarization defined for the spatial distribution (DOP-SD), we fully-quantitatively characterize the spectrally-resolved polarization states of arbitrary CP (axisymmetrically polarized and higher-order cylindrically polarized) broadband pulses generated by coherent beam combining. All the generated pulse states were fully-quantitatively analyzed for the first time and proved to have high symmetry (DOP-SD ≳ 0.95) and low spectral dependence of polarization states. Moreover, we show the DOP-SD, which cannot be defined by the conventional higher-order and hybrid Stokes parameters, enables us to make a quantitative evaluation of small degradation of rotational symmetry of polarization distribution. This quantitative characterization with high precision is significant for applications of precise material processing, quantum information processing, magneto-optical storage and nonlinear spectroscopic polarimetry.
Similar content being viewed by others
Introduction
A cylindrically polarized (CP) beam or Laguerre-Gauss (LG) vector vortex beam, a solution to the paraxial wave equation, is a laser beam mode which has rotational symmetry of the polarization distribution around the beam axis1. Its nonuniform polarization distribution has recently attracted much attention for applications such as telecommunications2,3,4, quantum information5,6,7, optical trapping8,9,10, physical properties measurement11,12, super-resolution microscopy13, detection of dielectric nano particles14, determination of orientation of point defects15 and laser processing16,17,18.
To realize these applications, many light sources and optical components generating CP beams have been developed19. Coherent beam combining methods20,21,22,23, being capable of generating arbitrary CP beams, are especially more versatile than other methods like direct producing from a resonator24,25,26,27 or using polarization converters28,29,30,31,32,33. To optimize the generation methods, it is crucial to establish quantitative evaluation method. For example, the purity evaluation of a CP beam is indispensable for the performance assessment of the application system using the CP beam, such as precision and reliability. However, almost all studies have made qualitative evaluation for CP beams. Chen et al.23 and D’Ambrosio et al.33 have characterized arbitrary CP beams by using the higher-order34,35 and the hybrid36 Stokes parameters. Not being able to define the degree of polarization37, these parameters cannot be responsible for the local deviation, in the symmetry of CP states, which often appears in experiments. As far as we know, all of the studies including their reports therefore did not make the fully-quantitative characterization of the generated CP beams, but qualitative or partly-quantitative characterization. In other words, the purity of CP beams generated so far has not been experimentally certified. To overcome these issues, we have proposed the extended Stokes parameters (ESPs) and their degree of polarization for the spatial distribution (DOP-SD; modified DOP)37,38 and have already shown their availability of quantitative characterization of l = 1 CP narrowband pulses38 (the pulses having C∞ symmetry of their transverse electric fields; the definition of l is described in our report37). In the present paper, to demonstrate the importance of the fully-quantitative characterization of CP beams, we generate l = 1 and l = 2 CP broadband pulses and make fully-quantitative spectrally-resolved characterization by using the ESPs and their DOP-SD. To our knowledge, the fully-quantitative characterization of various CP broadband pulse states is conducted for the first time. CP pulses recently began to be used in some applications such as material processing39 and nonlinear spectroscopic polarimetry40, where broadband or ultrashort CP pulses give us more information in the frequency or temporal domain. In this sense, the fully-quantitative characterization of broadband or ultrashort CP pulses here is significant.
Results and Discussions
Arbitrary manipulation of cylindrically polarized pulse states
We here describe the basic concept of generating arbitrary CP broadband pulses (Fig. 1(a)). The detail of the experimental setup is shown in Supplementary Fig. S1. First, x-polarized  broadband (or ultrashort) pulses are converted into x-polarized
broadband (or ultrashort) pulses are converted into x-polarized  optical vortex (OV) by the spatial light modulator in the 4-f configuration (4-f SLM). Here, l is referred to as the azimuthal index of LG modes41. A super-achromatic half-wave plate (HWP1) based on the design by Pancharatnam42 and a coherent combining system coherently superpose x-polarized
optical vortex (OV) by the spatial light modulator in the 4-f configuration (4-f SLM). Here, l is referred to as the azimuthal index of LG modes41. A super-achromatic half-wave plate (HWP1) based on the design by Pancharatnam42 and a coherent combining system coherently superpose x-polarized  and y-polarized
and y-polarized  OV broadband pulses, whose energy ratio is controlled by HWP1;
OV broadband pulses, whose energy ratio is controlled by HWP1;  . After that, the x- and y-polarized components of E3 are converted into
. After that, the x- and y-polarized components of E3 are converted into  and
and  circularly polarized states by a super-achromatic quarter-wave plate (QWP1), respectively. Here, s is the spin angular momentum of photon in units of ħ38. The pulse passes through a super-achromatic half-wave plate (HWP2), following which the sign of spin angular momentum of light is flipped36 and the relative phase between
circularly polarized states by a super-achromatic quarter-wave plate (QWP1), respectively. Here, s is the spin angular momentum of photon in units of ħ38. The pulse passes through a super-achromatic half-wave plate (HWP2), following which the sign of spin angular momentum of light is flipped36 and the relative phase between  and
and  states can be adjusted by the rotation angle of HWP2 θH2:
states can be adjusted by the rotation angle of HWP2 θH2:
(a) An outline drawing of generating arbitrary CP broadband pulses by use of coherent beam combining. SLM, a spatial light modulator; HWP1,2, super-achromatic half-wave plates; QWP1, a super-achromatic quarter-wave plate; In this figure, the case for m = 1, θH1 = π/8( = 22.5°), θH2 = −π/8( = −22.5°) is drawn. (b) The relationship of the rotational angles θH1 and θH2 to a generated beam state (m = 1).

which gives mth CP broadband pulses37. The normalized extended Stokes parameters (see Supplementary materials for definition) of the pulse state is

which is represented by the point (θ, ϕ) = (4θH1, π/2 + 4θH2) on the extended Poincaré sphere (Fig. 1(b)). Hence arbitrary manipulation of CP broadband pulse state can be achieved by adjusting the rotation angles of HWP1 and HWP2. In the present paper, we characterize generated pulse states and spatial symmetry by using parameters of the normalized extended Stokes vectors and the lth DOP-SD  , respectively. The definition of
, respectively. The definition of  is in Supplementary materials.
is in Supplementary materials.
Full quantitative analysis of cylindrically polarized states
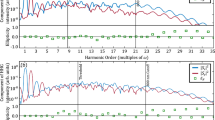
We respectively generated seven states for l = 1 and l = 2 CP broadband pulses: (θ, ϕ) = (0, 0), (π/4, 0), (π/4, π/4), (π/4, π/2), (π/2, 0), (π/2, π/4), (π/2, π/2). For simplicity, (θ, ϕ) is omitted hereafter. The light source used is a Ti:sapphire laser amplifier (center wavelength 800 nm, bandwidth of ~40 nm, pulse duration ~25 fs and repetition rate 1 kHz). Figure 2 shows characterization results for l = 1 (π/2, 0) and l = 2 (π/2, 0) CP pulses as typical examples. Spectrally-resolved polarization distributions are shown in Fig. 2(a,d); (a) is for l = 1 (π/2, 0) CP pulses (or radially polarized pulses) and (d) is for l = 2 (π/2, 0) CP pulses. From the polarization distributions in Fig. 2(a,d), the values of  (Fig. 2(b)) and
(Fig. 2(b)) and  (Fig. 2(c)) and
(Fig. 2(c)) and  (Fig. 2(e)) and
(Fig. 2(e)) and  (Fig. 2(f)) in individual spectral ranges were computed.
(Fig. 2(f)) in individual spectral ranges were computed.
Characterization results of l = 1 (a–c) and l = 2 (d–f) (π/2, 0) CP broadband pulses. (a,d) spectrally-resolved polarization distribution of generated l = 1 and l = 2 CP pulses, respectively. These polarization distributions are colored under the following rule: red, left-handed elliptical polarization; blue, right-handed elliptical polarization; black, linear polarization. The green points at the center of images represent the origins (x, y) = (0, 0). (b,c) characterization results of  and
and  for l = 1 (π/2, 0) CP pulses (or radially polarized pulses), respectively. (e,f) characterization results of
for l = 1 (π/2, 0) CP pulses (or radially polarized pulses), respectively. (e,f) characterization results of  and
and  for l = 2 (π/2, 0) CP pulses, respectively.
for l = 2 (π/2, 0) CP pulses, respectively.
The characterization results for all states are described in Fig. 3; (a) and (b) are for l = 1 CP pulse states and (c) and (d) are for l = 2 CP pulse states. Figure 3(a,c) respectively represent the l = 1 and l = 2 extended Poincaré sphere, on which the spectrally-resolved values of normalized ESPs  and
and  in l = 1 and l = 2 CP states are plotted. The spectrally-resolved values of DOP-SD corresponding to the CP states in Fig. 3(a,c) are shown in Fig. 3(b,d), respectively.
in l = 1 and l = 2 CP states are plotted. The spectrally-resolved values of DOP-SD corresponding to the CP states in Fig. 3(a,c) are shown in Fig. 3(b,d), respectively.
Spectrally-resolved characterization results for l = 1 (a,b) and l = 2 (c,d) CP pulses. The seven CP pulse states are realized in every azimuthal index l. (a,c) The values of normalized ESPs  for l = 1 and l = 2 CP pulse states plotted on the extended Poincaré sphere, respectively. (b,d) DOP-SD
for l = 1 and l = 2 CP pulse states plotted on the extended Poincaré sphere, respectively. (b,d) DOP-SD  of l = 1 and l = 2 CP pulse states corresponding to (a,c), respectively.
of l = 1 and l = 2 CP pulse states corresponding to (a,c), respectively.
All polarization distributions of l = 1 (π/2, 0) CP pulses at measured wavelengths (780, 790, 800, 810 and 820 nm) in Fig. 2(a) are almost purely radially polarized. This fact is well indicated by the obtained results that  and
and  were respectively over 0.99 and 0.98 in all spectral regions (Fig. 2(b,c)). Since
were respectively over 0.99 and 0.98 in all spectral regions (Fig. 2(b,c)). Since  is associated with the energy ratio between (π/2, 0) (radially polarized) state and (π/2, π) (azimuthally polarized) state38, which is given by
is associated with the energy ratio between (π/2, 0) (radially polarized) state and (π/2, π) (azimuthally polarized) state38, which is given by  , over 99% energy of the temporally- and spatially-perfect-polarized37 (TSPP) state was radially polarized. Moreover, DOP-SD
, over 99% energy of the temporally- and spatially-perfect-polarized37 (TSPP) state was radially polarized. Moreover, DOP-SD  enables us to evaluate the over 98% of the temporally-perfect-polarized state of the generated pulses were TSPP state. Consequently, the pulses generated from a coherent combining system had high purity of l = 1 (π/2, 0) CP state and high symmetry of polarization distribution.
enables us to evaluate the over 98% of the temporally-perfect-polarized state of the generated pulses were TSPP state. Consequently, the pulses generated from a coherent combining system had high purity of l = 1 (π/2, 0) CP state and high symmetry of polarization distribution.
From Fig. 2(e,f), l = 2 (π/2, 0) CP pulses similarly had high purity (over 99% in energy ratio) of l = 2 (π/2, 0) CP state and high symmetry (around 97% in energy ratio) in l = 2 CP state, though l = 2 pulses were slightly inferior to l = 1 pulses with regard to symmetry. Contamination of elliptical polarization in the polarization distribution (Fig. 2(d)) apparently affects the degradation in DOP-SD compared to that of l = 1 (π/2, 0) CP pulses.
The contamination comes from two factors. One is the deformation of incident OV pulses into the coherent combining system; the other is the degradation of extinction ratio of the polarizing beam splitter in the coherent combining system because of inclining incident angle. Figure 4(a–d) respectively depict the intensity and polarization distributions of (l, θH1) = (1, 0), (1, π/4), (2, 0) and (2, π/4) cases. The measurements of Fig. 4(a,c) and (b,d) are respectively conducted under blocking the blue blanch and the magenta branch in Supplementary Fig. S1, which means E5 should be proportional to  and
and  . However, these intensity distributions are of twofold symmetry rather than axisymmetry. This result is attributed to the slight superimposition of
. However, these intensity distributions are of twofold symmetry rather than axisymmetry. This result is attributed to the slight superimposition of  component on
component on  OV pulses because of deformation passing through optic elements. Though the polarization distribution should be circularly polarized, the polarization states are elliptic. The fact can be ascribed to the degradation of extinction ratio of the polarizing beam splitter in the coherent combining system because of inclining incident angle (in other words, the contamination of s- and p-polarized components at the polarizing beam splitter). The actual electric field of E5 is approximately described as
OV pulses because of deformation passing through optic elements. Though the polarization distribution should be circularly polarized, the polarization states are elliptic. The fact can be ascribed to the degradation of extinction ratio of the polarizing beam splitter in the coherent combining system because of inclining incident angle (in other words, the contamination of s- and p-polarized components at the polarizing beam splitter). The actual electric field of E5 is approximately described as
(a–d) The intensity and polarization distributions of (l, θH1) = (a) (1, 0), (b) (1, π/4), (c) (2, 0) and (d) (2, π/4) cases. The experimental measurements of (a,c) and (b,d) are conducted under blocking the blue blanch and the magenta branch in Supplementary Fig. S1, respectively. The white and black arrows are placed to emphasize the twofold symmetry of the intensity patterns. All the polarization distributions are colored under the rule in Fig. 2.

where δ1,2,4,5 and δ3,6 are superposition coefficients associated with the deformation and the elliptical polarization, respectively. When m = 1, the individual unwanted terms 
 and
and  can be partly cancelled. However, in the m = 2 case, the unwanted terms are
can be partly cancelled. However, in the m = 2 case, the unwanted terms are  and
and  , which cannot be cancelled. The contamination of terms except
, which cannot be cancelled. The contamination of terms except  and
and  leads to degradation of C|m−1| rotational symmetry. The value of DOP-SD of l = 2 CP pulses are thus smaller than that of l = 1 pulses.
leads to degradation of C|m−1| rotational symmetry. The value of DOP-SD of l = 2 CP pulses are thus smaller than that of l = 1 pulses.
Figure 3(a,c) respectively indicate the spectral dependence of polarization states of l = 1 and l = 2 CP pulses. All the pulse states have quite low spectral dependences thanks to optics for broadband pulses such as super-achromatic wave plates and a low-group-velocity-dispersion polarizing beam splitter. All the values of DOP-SD for l = 1 and l = 2 CP pulses have low spectral dependence ( ≲ 0.01), while the DOP-SD values for l = 2 CP pulses are somewhat less than those for l = 1 CP pulses by 0.02 to 0.03 (Fig. 3(b,d)) because of the previously described reasons. These results clearly show that our system employing coherent beam combining is able to generate arbitrary CP broadband pulse states with high symmetry and low spectral dependence, which is fully-quantitatively investigated by ESPs and DOP-SD with high precision.
≲ 0.01), while the DOP-SD values for l = 2 CP pulses are somewhat less than those for l = 1 CP pulses by 0.02 to 0.03 (Fig. 3(b,d)) because of the previously described reasons. These results clearly show that our system employing coherent beam combining is able to generate arbitrary CP broadband pulse states with high symmetry and low spectral dependence, which is fully-quantitatively investigated by ESPs and DOP-SD with high precision.
Comparison with simulation
In this section, we mention the comparison between the experimental and the simulation results. We conducted simulation for l = 1 (π/2, 0) and l = 2 (π/2, 0) CP states. The simulation results are shown in Fig. 5(a,b) and Table 1. Both intensity and polarization distributions in Fig. 5(a,b) well agree with that of the experimental results for l = 1 (π/2, 0) (Fig. 2(a)) and l = 2 (π/2, 0) (Fig. 2(d)) states, respectively. The values of  and DOP-SD
and DOP-SD  in Table 1 are also in good agreement with the experimental results in Fig. 2(b,e) and (c,f), respectively. In particular, there is a small (~0.02) difference between l = 1 and l = 2 cases in the simulation results for DOP-SD, which also appears in the experimental results. Therefore, it should be stressed that our measurement method is able to detect such small asymmetricity.
in Table 1 are also in good agreement with the experimental results in Fig. 2(b,e) and (c,f), respectively. In particular, there is a small (~0.02) difference between l = 1 and l = 2 cases in the simulation results for DOP-SD, which also appears in the experimental results. Therefore, it should be stressed that our measurement method is able to detect such small asymmetricity.
 and DOP-SD
and DOP-SD  .
.The simulation results for (a) l = 1 (π/2, 0) and (b) l = 2 (π/2, 0) pulse states. All the polarization distributions are colored under the rule in Fig. 2.
Perspective
It has been pointed out that precise measurement of polarization state is important in quantum information43. Applications using polarized pulses such as material processing44, magneto-optical storage45 and nonlinear spectroscopic polarimetry40 also need to know their polarization states precisely. Using CP pulses instead of the conventional uniform polarized pulses is a manner to extend the degree of freedom in these applications, which have been already demonstrated in quantum information science5,6,7, material processing16 and nonlinear spectroscopic polarimetry40. Our fully-quantitative measurement method for CP pulses hence can improve the sophistication of these applications.
We think that frequency chirp compensation can be easily achieved because of optics components for broadband pulses in our system. Characterization results in Fig. 3(a,c) show that the dispersions of spectrally-resolved polarization states in individual CP pulse states are small (≲0.05 in propagation distance on the extended Poincaré sphere). CP ultrashort pulses with steady polarization state in the pulse duration, which is especially important for applications for magneto-optical storage and nonlinear spectroscopic polarimetry, can be therefore generated with our system. Our experimental setup, where the accessible spectral range covers the region from 690 nm to 1080 nm (limited by the polarizing beam splitter and half-wave plates), offers us the capability of generating ultrashort CP pulses below 10 fs without polarization distribution dispersion. Moreover, by insertion of a femtosecond polarization pulse shaper46 after the 4-f SLM system, in place of HWP1 and HWP2, our experimental setup will be able to generate the CP pulses with arbitrary control of temporal CP states on one extended Poincaré sphere. Although the issue of fully-spatiotemporal characterization method for ultrashort pulses with nonuniform polarization distribution still remains, our measurement method is quite useful for precise characterization of ultrashort pulses.
The good agreement between the experimental and simulation results indicates that the degradation in DOP-SD is ascribed to the deformation of incident OV pulses and the contamination of perpendicular polarized components at the polarizing beam splitter and ensures that we can quantitatively investigate even the small differences of rotational symmetry of polarization distributions or the small contamination of unwanted modes by using DOP-SD. At least  is significant and detectable in our measurement system. Though the earlier studies have not taken account of DOP-SD, DOP-SD as well as ESPs is an important parameter for full-quantitative characterization of CP states.
is significant and detectable in our measurement system. Though the earlier studies have not taken account of DOP-SD, DOP-SD as well as ESPs is an important parameter for full-quantitative characterization of CP states.
Methods
Generation of broadband optical vortex pulses
The generated pulses from a Ti:sapphire laser amplifier are attenuated by ND filters, following which the 4-f SLM converts into x-polarized l = 1, p = 0 or l = 2, p = 0 OV pulses. Here, p denotes the radial index of LG modes41. The 4-f configuration in the SLM system enables us to compensate for angular dispersion47,48. We furthermore utilize a complex-amplitude modulation technique with a phase-only SLM49,50 as means to convert to broadband arbitrary single LG mode OV pulses.
Finding the zero delay in the coherent combining system
Using a polarizer (POL2 in Supplementary Fig. S1) and a spectrometer, we find the zero delay with the aid of the spectrum interference method. A charge-coupled-devise (CCD1 in Supplementary Fig. S1) monitors the intensity profile of the x-polarized component of E4 in order to ensure the delay time is unchanged within the polarization measurement.
Measuring polarization distributions
In the polarization measurement system, the pulses are spectrally-resolved by bandpass filters (BPF in Supplementary Fig. S1; center wavelengths, 780, 790, 800, 810, 820 nm; bandwidths, 10 nm), then their polarization distributions are acquired by using a rotating-retarder type imaging polarimeter51, which is composed of an achromatic quarter-wave plate (QWP2 in Supplementary Fig. S1), a Glan-Laser polarizer (GLP in Supplementary Fig. S1) and a charge-coupled-devise camera (CCD2 in Supplementary Fig. S1). From the polarization distribution, we computed the normalized extended Stokes vectors  and the mth DOP-SD
and the mth DOP-SD  . Here, the origins (x, y) = (0, 0) on the recorded images are set to maximize the mth DOP-SD.
. Here, the origins (x, y) = (0, 0) on the recorded images are set to maximize the mth DOP-SD.
Simulation
We respectively evaluated δ1,2,4,5 and δ3,6 from the intensity and the polarization distributions in Fig. 4(a–d) (the values are in Table 1). The intensity distributions were plotted by using the following equation based on equation 3:

where (r, ϕ) is the circular polar coordinates and w is a parameter for the beam size. We have made simulations under the various conditions of δ1,2,4,5 and confirmed that the values of  and
and  hardly changed.
hardly changed.
Additional Information
How to cite this article: Suzuki, M. et al. Full Quantitative Analysis of Arbitrary Cylindrically Polarized Pulses by Using Extended Stokes Parameters. Sci. Rep. 5, 17797; doi: 10.1038/srep17797 (2015).
References
Tovar, A. A. Production and propagation of cylindrically polarized Laguerre-Gaussian laser beams. J. Opt. Soc. Am. A 15, 2705–2711 (1998).
Ramachandran, S., Kristensen, P. & Yan, M. F. Generation and propagation of radially polarized beams in optical fibers. Opt. Lett. 34, 2525–2527 (2009).
Bozinovic, N. et al. Terabit-scale orbital angular momentum mode division multiplexing in fibers. Science 340, 1545–1548 (2013).
Milione, G. et al. 4 × 20 Gbit/s mode division multiplexing over free space using vector modes and a q-plate mode (de)multiplexer. Opt. Lett. 40, 1980–1983 (2015).
Barreiro, J. T., Wei, T.-C. & Kwiat, P. G. Remote preparation of single-photon “hybrid” entangled and vector-polarization states. Phys. Rev. Lett. 105, 030407 (2010).
Gabriel, C. et al. Entangling different degrees of freedom by quadrature squeezing cylindrically polarized modes. Phys. Rev. Lett. 106, 060502 (2011).
Parigi, V. et al. Storage and retrieval of vector beams of light in a multiple-degree-of-freedom quantum memory. Nat. Commun. 6, 7706 (2015).
MacDonald, M. P. et al. Creation and manipulation of three-dimensional optically trapped structures. Science 296, 1101–1103 (2002).
Huang, K. et al. Vector-vortex Bessel-Gauss beams and their tightly focusing properties. Opt. Lett. 36, 888–890 (2011).
Ito, S. et al. Selective optical assembly of highly uniform nanoparticles by doughnut-shaped beams. Sci. Rep. 3 (2013).
Tokizane, Y. et al. Global evaluation of closed-loop electron dynamics in quasi-one-dimensional conductors using polarization vortices. Opt. Express 17, 24198–24207 (2009).
Fatemi, F. K. Cylindrical vector beams for rapid polarization-dependent measurements in atomic systems. Opt. Express 19, 25143–25150 (2011).
Novotny, L., Beversluis, M. R., Youngworth, K. S. & Brown, T. G. Longitudinal field modes probed by single molecules. Phys. Rev. Lett. 86, 5251–5254 (2001).
Roy, S., Ushakova, K., van den Berg, Q., Pereira, S. F. & Urbach, H. P. Radially polarized light for detection and nanolocalization of dielectric particles on a planar substrate. Phys. Rev. Lett. 114, 103903 (2015).
Dolan, P. R., Li, X., Storteboom, J. & Gu, M. Complete determination of the orientation of NV centers with radially polarized beams. Opt. Express 22, 4379–4387 (2014).
Hnatovsky, C., Shvedov, V., Krolikowski, W. & Rode, A. Revealing local field structure of focused ultrashort pulses. Phys. Rev. Lett. 106, 123901 (2011).
Toyoda, K. et al. Transfer of light helicity to nanostructures. Phys. Rev. Lett. 110, 143603 (2013).
Omatsu, T. et al. Metal microneedle fabrication using twisted light with spin. Opt. Express 18, 17967–17973 (2010).
Zhan, Q. Cylindrical vector beams: from mathematical concepts to applications. Adv. Opt. Photon. 1, 1–57 (2009).
Tidwell, S. C., Kim, G. H. & Kimura, W. D. Efficient radially polarized laser beam generation with a double interferometer. Appl. Opt. 32, 5222–5229 (1993).
Niziev, V. G., Chang, R. S. & Nesterov, A. V. Generation of inhomogeneously polarized laser beams by use of a Sagnac interferometer. Appl. Opt. 45, 8393–8399 (2006).
Maurer, C., Jesacher, A., Fürhapter, S., Bernet, S. & Ritsch-Marte, M. Tailoring of arbitrary optical vector beams. New Journal of Physics 9, 78 (2007).
Chen, S. et al. Generation of arbitrary cylindrical vector beams on the higher order Poincaré sphere. Opt. Lett. 39, 5274–5276 (2014).
Kozawa, Y. & Sato, S. Generation of a radially polarized laser beam by use of a conical brewster prism. Opt. Lett. 30, 3063–3065 (2005).
Yonezawa, K., Kozawa, Y. & Sato, S. Generation of a radially polarized laser beam by use of the birefringence of a c-cut Nd:YVO4 crystal. Opt. Lett. 31, 2151–2153 (2006).
Ahmed, M. A., Voss, A., Vogel, M. M. & Graf, T. Multilayer polarizing grating mirror used for the generation of radial polarization in Yb;YAG thin-disk lasers. Opt. Lett. 32, 3272–3274 (2007).
Hamazaki, J., Kawamoto, A., Morita, R. & Omatsu, T. Direct production of high-power radially polarized output from a side-pumped Nd:YVO4 bounce amplifier using a photonic crystal mirror. Opt. Express 16, 10762–10768 (2008).
Machavariani, G., Lumer, Y., Moshe, I., Meir, A. & Jackel, S. Efficient extracavity generation of radially and azimuthally polarized beams. Opt. Lett. 32, 1468–1470 (2007).
Wakayama, T., Komaki, K., Otani, Y. & Yoshizawa, T. Achromatic axially symmetric wave plate. Opt. Express 20, 29260–29265 (2012).
Cardano, F. et al. Polarization pattern of vector vortex beams generated by q-plates with different topological charges. Appl. Opt. 51, C1–C6 (2012).
Imai, R. et al. Terahertz vector beam generation using segmented nonlinear optical crystals with threefold rotational symmetry. Opt. Express 20, 21896–21904 (2012).
Carbajo, S. et al. Efficient generation of ultra-intense few-cycle radially polarized laser pulses. Opt. Lett. 39, 2487–2490 (2014).
D’Ambrosio, V., Baccari, F., Slussarenko, S., Marrucci, L. & Sciarrino, F. Arbitrary, direct and deterministic manipulation of vector beams via electrically-tuned q-plates. Sci. Rep. 5 (2015).
Milione, G., Sztul, H. I., Nolan, D. A. & Alfano, R. R. Higher-order Poincaré sphere, Stokes parameters and the angular momentum of light. Phys. Rev. Lett. 107, 053601 (2011).
Milione, G., Evans, S., Nolan, D. A. & Alfano, R. R. Higher order Pancharatnam-Berry phase and the angular momentum of light. Phys. Rev. Lett. 108, 190401 (2012).
Holleczek, A., Aiello, A., Gabriel, C., Marquardt, C. & Leuchs, G. Classical and quantum properties of cylindrically polarized states of light. Opt. Express 19, 9714–9736 (2011).
Suzuki, M., Yamane, K., Oka, K., Toda, Y. & Morita, R. Extended Stokes parameters for cylindrically polarized beams. Optical Review 22, 179–183 (2015).
Suzuki, M., Yamane, K., Oka, K., Toda, Y. & Morita, R. Nonlinear coupling between axisymmetrically-polarized ultrashort optical pulses in a uniaxial crystal. Opt. Express 22, 16903–16915 (2014).
Hnatovsky, C., Shvedov, V., Krolikowski, W. & Rode, A. Revealing local field structure of focused ultrashort pulses. Phys. Rev. Lett. 106, 123901 (2011).
Shigematsu, K. et al. Coherent dynamics of uniaxially-strained GAN excitons excited by cylindrically polarized pulses. In Conference on Lasers and Electro-Optics/Europe and the European Quantum Electronics Conference, EE-P.15 (Munich, Germany, 2015).
Allen, L., Beijersbergen, M. W., Spreeuw, R. J. C. & Woerdman, J. P. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A 45, 8185–8189 (1992).
Pancharatnam, S. Achromatic combinations of birefringent plates. Proceedings of the Indian Academy of Sciences - Section A 41, 137–144 (1955).
Salvail, J. Z. et al. Full characterization of polarization states of light via direct measurement. Nat. Photon. 7, 316–321 (2013).
Shimotsuma, Y., Kazansky, P. G., Qiu, J. & Hirao, K. Self-organized nanogratings in glass irradiated by ultrashort light pulses. Phys. Rev. Lett. 91, 247405 (2003).
Satoh, T., Iida, R., Higuchi, T., Fiebig, M. & Shimura, T. Writing and reading of an arbitrary optical polarization state in an antiferromagnet. Nat. Photon. 9, 25–29 (2015).
Brixner, T. & Gerber, G. Femtosecond polarization pulse shaping. Opt. Lett. 26, 557–559 (2001).
Mariyenko, I., Strohaber, J. & Uiterwaal, C. Creation of optical vortices in femtosecond pulses. Opt. Express 13, 7599–7608 (2005).
Zeylikovich, I., Sztul, H. I., Kartazaev, V., Le, T. & Alfano, R. R. Ultrashort Laguerre-Gaussian pulses with angular and group velocity dispersion compensation. Opt. Lett. 32, 2025–2027 (2007).
Davis, J. A., Cottrell, D. M., Campos, J., Yzuel, M. J. & Moreno, I. Encoding amplitude information onto phase-only filters. Appl. Opt. 38, 5004–5013 (1999).
Ando, T., Ohtake, Y., Matsumoto, N., Inoue, T. & Fukuchi, N. Mode purities of Laguerre-Gaussian beams generated via complex-amplitude modulation using phase-only spatial light modulators. Opt. Lett. 34, 34–36 (2009).
Collett, E. Polarized light in fiber optics, 365–368 (SPIE Press, New Jersey, 2003).
Acknowledgements
This work was partially supported by Grant-in-Aid for Scientific Research (B) (No. 26286056, 2014–2016) from Japan Society for the Promotion of Science (JSPS) and CREST, JST. M.S. acknowledges support from JSPS Research Fellowships (No. 15J00038).
Author information
Authors and Affiliations
Contributions
M.S. conducted the experiment and the simulation and analyzed these results. K.Y. designed and built the coherent combining system. K.O. conceived the arbitrary manipulation of cylindrically polarized pulse states. M.S. and R.M. wrote the main manuscript text. Y.T. and R.M. supervised the implementation. All the authors discussed the results and reviewed the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Suzuki, M., Yamane, K., Oka, K. et al. Full Quantitative Analysis of Arbitrary Cylindrically Polarized Pulses by Using Extended Stokes Parameters. Sci Rep 5, 17797 (2016). https://doi.org/10.1038/srep17797
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep17797
This article is cited by
-
Comprehensive quantitative analysis of vector beam states based on vector field reconstruction
Scientific Reports (2019)
-
Spin-dependent manipulating of vector beams by tailoring polarization
Scientific Reports (2016)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.