Abstract
Microfluidic devices can be used to execute a variety of continuous flow analytical and synthetic chemistry protocols with a great degree of precision. The growing availability of additive manufacturing has enabled the design of microfluidic devices with new functionality and complexity. However, these devices are prone to larger manufacturing variation than is typical of those made with micromachining or soft lithography. In this report, we demonstrate a design-for-manufacturing workflow that addresses performance variation at the microfluidic element and circuit level, in context of mass-manufacturing and additive manufacturing. Our approach relies on discrete microfluidic elements that are characterized by their terminal hydraulic resistance and associated tolerance. Network analysis is employed to construct simple analytical design rules for model microfluidic circuits. Monte Carlo analysis is employed at both the individual element and circuit level to establish expected performance metrics for several specific circuit configurations. A protocol based on osmometry is used to experimentally probe mixing behavior in circuits in order to validate these approaches. The overall workflow is applied to two application circuits with immediate use at on the bench-top: series and parallel mixing circuits that are modularly programmable, virtually predictable, highly precise and operable by hand.
Similar content being viewed by others
Introduction
Additive manufacturing is rapidly becoming a viable alternative to micromachining and soft lithography for fabricating micro- and milli-fluidic devices1,2,3,4,5. Methods such as stereolithography (SLA) or extrusion-based processes (e.g. fused-deposition modeling, or FDM) enable entire devices with non-planar channel geometries to be fabricated rapidly and with less resources relative to traditional methods6. However, additive manufacturing is generally less precise than micromachining, leading to the possibility of performance errors in microfluidic systems designed to precisely control fluid transport and mixing. The impact of manufacturing variability on microfluidic circuit functions has not been explored quantitatively in the literature; errors in concentration of flows in complex microfluidic networks are generally unpredictable and must be addressed on a case-by-case, ad hoc basis. Additive manufacturing makes this sort of quantitative analysis possible by introducing a standardized fabrication technology as well as by encoding microfluidic system designs as digital, machine-interpreted files.
Previously, we introduced a platform of self-aligned discrete microfluidic elements manufactured using SLA that are reversibly connectable and described by their terminal flow characteristics much like discrete elements in electronic systems7. This system lends itself to the construction of reconfigurable, modular, three-dimensionally complex and hierarchically designed microfluidic devices from a library of standardized components suitable for mass manufacturing. In this work, we develop this system further by demonstrating a virtual implementation strategy and experimental probing procedure that address predicting variations in performance. This strategy has three parts: (A) definition of a component library of passive elements qualified by their expected variation due to manufacturing, (B) network analysis to derive mixing operability of some simple microfluidic circuits with useful application on the bench-top and (C) prediction of network performance variation using statistical analysis methods.
In (A), we develop an element library that is intuitively compatible with linear circuit analysis and accompanying statistical analysis techniques; hydraulic resistance values of each element were selected with convenience for designers in mind. Channel geometry was then deduced in order to yield these well-defined values of hydraulic resistance. In (B), microfluidic circuit topologies for source-invariant parallel and series mixing were conceived of and characterized by simple mathematical rules as a model system for network analysis. Network analysis is a powerful method for gaining insight into the operation of monolithic microfluidic circuits (see8,9,10,11,12,13 for a diverse set of examples), but in general has not been used as a central tool for design. In (C), a complete virtual implementation of each microfluidic circuit was devised, including expected manufacturing variation in components, in order to simulate the realistic scenarios for network performance. This was accomplished through applying mechanistic understanding of stereolithography to the statistical calculation of hydraulic resistance tolerances at the module level in (A) and further applying understanding of module level tolerances to the network analysis performed in (B). Ultimately, experimental realizations of these mixing circuits were assembled and probed using osmotic solutions in order to validate these models.
Application Circuits
A fundamental process in analytical and synthetic chemistry is the mixing of small quantities of fluids. Typically, this is accomplished using syringes, pipettes, burettes and a number of other glass and plastic tools that are operated by hand to manually withdraw fluids from source containers and procedurally deposit them into a sample container. The error in the final composition of a mixture is largely attributed to error in operating these tools, or “source-variant” and can have serious consequences on the repeatability of procedures critical to research and clinical activities. Consequently, electronically controlled robotic systems that automate these procedural tasks have been developed in order alleviate operator-induced error, create better consistency in the physical operation of instruments and speed up processing of samples overall. These systems are often prohibitively expensive, carry a large learning curve and require significant infrastructural support. There is therefore a need for hand-held tools for precise, predictable mixing of low volume solutions that are insensitive to typical operator and instrument errors, or “source-invariant”. The model circuits presented in this work are designed to serve this practical need, leveraging the reconfigurable and resistance-centric aspects of our overall discrete element system, while borrowing inspiration from the large volume of microfluidic mixing circuit design literature available14,15,16,17. Microfluidic technologies for controlled mixing and dilution demonstrated in the literature thus far have been focused on the generation of concentration gradients that mimic biologically relevant fluidic environments. Devices capable of performing parallel and serial mixing18 multi-layer dilutions19 and logarithmic concentration gradients20 have provided microfluidic chip designers with several strategies for manipulating the concentration of solutions. While these methods represent a substantial effort to construct application-specific microfluidic circuits, few of these techniques make it simple for designers to tune mixing factors in a modular sense.
Results and Discussion
Microfluidic Resistor Element Library
Laminar microscale flows can be analyzed in terms of their hydraulic resistance as determined by channel size and morphology8. In other words, it is possible to develop a set of fluidic elements with varying channel size that are defined on the basis of total hydraulic resistance per component. We therefore developed a library of microfluidic channel elements categorized by their hydraulic resistance in a manner that allows designers to rapidly prototype designs on paper (Fig. 1). Channel sizes were restricted such that the Reynolds Number of each element was strictly indicative of laminar flow for rates as high as 200 mL/hr. The community practices set by manufacturers of standardized discrete electronic resistors was adopted, wherein a typical functional unit of resistance is two to three orders of magnitude larger than that of the so-called “parasitic” resistance in a wire.
Library of constructed discrete elements organized according to their designed hydraulic resistance, with units denoted as G, short for GPa-s-m−3.
Resistor class components were designed with a 642.5 μm channel side-length, allowing resistance to be manipulated by channel length that is achieved by snaking and coiling channels within individual resistance components. Expected Resistance and Error (2σ) determined through Monte Carlo Analysis from measured channel side length, which statistically ensures that 95% of designed components will fall within the stated resistance tolerance.
Consider the hydraulic resistance of a segment of straight channel with square cross-section (1)8:

Here, the length of a channel segment is given by L, the height or width of the cross-section is h and the dynamic viscosity of the conducted fluid is η. For the purposes of this study, the definition of such elements is restricted to the flow of pure water, at 20 °C, the temperature of our experiments. Therefore, a value of 1 mPa · s was used for η throughout. We define a unit of hydraulic resistance “G” as short-hand notation for 1 GPa-s-m–3. This corresponds to the resistance of a reference channel element of 6 mm length and 642.5 μm square cross-sectional height. This channel height was selected for its convenience in creating a system of resistors with values on a standard scale of integers or simple fractions. This approach was borrowed from a similar practice in discrete electronic components, wherein manufacturers primarily offer electronic resistors with values that allow for easy combination and selection by designers during the drafting of circuit schematics.
A variety of hydraulic resistor elements were constructed based on the reference 642.5 μm process height. Resistors larger than 1G were realized by snaking and coiling longer track lengths into a standardized cubic element footprint. A special class of wire-like components characterized by a 0.01 G parasitic resistance were developed by increasing the cross-section side length to 2.0317 mm such that flow conditions are still laminar at reasonably high flow rates (e.g. Re ~ 0.1 at 200 ml/h in the standard 6 mm reference length). Port elements for interfacing to circuits were constructed with a special height of 1.1425 mm, resulting in a parasitic resistance of 0.05 G. These stray millifluidic resistances are sufficiently less than resistor class microfluidic components such that they need not be considered in microfluidic network analysis during the design phase.
Determination of Resistor Tolerance from Statistical Methods
The error in resistance for each element was determined from the errors associated with the stereolithographic manufacturing process. Consider the hydraulic resistance of a channel segment of rectangular cross-section height h, width w and length L given in (2) and derived by solving the Navier-Stokes equation using a Fourier Series method8:

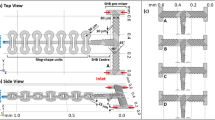
The layer-by-layer stereolithographic printing method affects manufacturing tolerances/errors Δw, ΔL and Δh due to the direction in which a channel segment is arranged with respect to the printing process (Fig. 2). This implies that the error in Δxy due to the printing optics and related control mechanism that affects the so-called “xy print plane” will be different than the error Δz due to the mechanism that controls the addition of photoresin layers along the “z print axis”. This results in channels that are imperfectly rectangular despite their square design. In addition, the solidification of material during printing and in post-processing may cause further anisotropic deformation of the channel. These effects appear to be secondary to those resulting from controls mechanisms in the printer, but the characterization procedure described here is translatable across variety of additive manufacturing processes and materials beyond those demonstrated experimentally. Experimental values for the print plane and print axis tolerances were determined by constructing a large number of library components with a model material (see Materials and Methods) and optically measuring their geometric cross sections (Supplementary Figure 1). These tolerances were used in a Monte Carlo simulation to predict the standard deviation in hydraulic resistance of each element in the component library (see Materials and Methods Section). Briefly, the resistance of each channel segment constituting a given element was computed using (2) with parameters w, L and h drawn from pseudorandom normal distributions set by the tolerances Δxy and Δz depending on the orientation of that segment (Fig. 2b). The segment resistances were added in series such that final resistance for the element was computed for that particular set of draws. Ultimately, the “manufacturer’s tolerance”, or 2σ, for 5000 draws was determined such that 95% of constructed resistor elements will fall within the specified range of values (Fig. 1).
(a) Port opening with centered channel for a resistance component with 642.5 μm cross-sectional side length showing the precision in the print plane, xy and the precision in the print axis, z. Due to the control mechanisms of stereolithography, precision in the xy and z plane are expected to be different. (b) Total component resistance was approximated by determining and adding together the resistance of segments respective to the xy-planes (yellow lines) and z-plane (purple lines). Both planes carry a particular fabrication error, determined by optically measuring the cross-sectional side length of components and creating distributions of precisions in both orientations (see Supplementary Figure 1).
Circuit Topologies for Parallel and Series Mixing
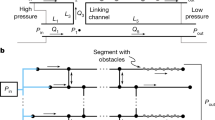
This study considers two microfluidic circuit topologies, denoted as Fork (Fig. 3a) and Ladder (Fig. 3b), respectively capable of parallel and series mixing. Reagents are pulled through inlet branches by a negative flow-rate source, such that they combine at a common junction to yield the target mixture. Borrowing from the hydraulic analogy to electrical circuits8, the Fork topology employs the principles of parallel resistances, wherein the pressure drop seen across each input branch is equivalent. In turn, the flow rate developed across each branch is due solely to the selection of branch resistances. This allows for a system where the resulting volume fraction of each inlet fluid at the outlet is invariant to the flow rate. The Ladder topology enjoys similar independence from source variation, but represents an alternate scenario in which inlet reagents are mixed serially. Flow through the branch furthest from the source is mixed with the next adjacent branch, which is then mixed with the next adjacent branch, so on and so forth until the final mixture is created at the outlet. In other words, the Ladder topology can be thought of as recursively connected Fork topologies.
(a) Generalized Fork topology where each branch resistance experiences the same pressure drop across and mixing occurs in parallel between inputs. (b) Generalized Ladder topology where mixing occurs in a serial manner, such that branch R1 mixes with branch R2, which then passes through a mixing resistance, RM and further mixes with the next adjacent branch, until branch RN is reached.
Network Analysis and Characterization of Performance from Statistical Methods
We employed nodal analysis to study the operation of 2- and 3-inlet Fork circuits, as well as a 3-inlet Ladder circuit (Supplementary Notes 1–6). The design objective was stated in terms of χ, the volume fraction of a given inlet fluid in the outlet mixture. Design rules for χ for each inlet were in turn derived, showing how branch resistances can be selected in order to tune operation to deliver a given mixture of each feed fluid (Table 1). Note that the source-invariance of each configuration is apparent in each mixing rule: χ only depends on the choice of resistor and not the withdrawal flow rate. Each circuit was then constructed using a variety of resistor combinations (Table 2a–c) and tested by running a stock NaCl solution through a single branch of each topology (see Materials and Methods Section). The resulting dilutions of the stock solution were tested using osmometry, for which the stock solution was well suited to provide results with variance far below that of the predicted manufacturing variance in network operation.
A feature of board-level electronic circuit design that enables efficient and repeatable design and manufacturing is the use of statistical methods to predict circuit behavior due to error in terminal characteristics at the element level. Similarly, the tolerance of hydraulic resistors becomes important for predicting the operation of microfluidic circuits assembled from mass-manufactured standardized elements. While simple error analysis is sufficient for most circuits involving few nodes and input reagents, complex networks are hard to analyze by hand. This analysis can be automated using numerical techniques. We extended our use of Monte Carlo analysis at the element level to simulate expected performance at the circuit level. More specifically, we generated simulated bins of pseudorandom normally distributed discrete microfluidic resistors using the tolerances derived in Fig. 1 and computed the distribution of possible outlet volume fractions using the rules in Table 1. The resulting volume fractions were analyzed for the inlet of the first branch (Branch R1) of each circuit topology, which was fed by the stock NaCl solution.
Experimental Validation
The 2,3-inlet Fork and 3-inlet Ladder circuits were assembled (Figs 4, 5, 6) from the library of modular microfluidic devices (Fig. 1) with the configurations given in Table 2. The volume fraction of inlet reagents was validated for each configuration by introducing a “probe” solution of measurable concentration to a single inlet, which is then mixed with diluent from remaining inlets in the circuit and the outlet concentration is finally measured. Each circuit was constructed including an inlet resistance determined by 24.4 mm PEEK tubing (OD 1/16”). The 0.34 M NaCl probe solution was run through the branch denoted as R1 in each circuit and all other inlets were fed by Milli-Q water. After channels were primed by manual withdrawal, the syringe barrel was interchanged with a clean barrel to collect roughly 0.5–1 mL of resultant mixture. Osmolality of the diluted NaCl solution product was measured (see Materials and Methods), allowing for determination the volume fraction for each resistance combination, for all topologies, for three syringe barrel exchanges (effectively three repetitions). Note that the measured output volume fractions (as determined by osmometry to find NaCl concentration in the output) fall within the predicted range of variation from as-designed resistance values. In Fig. 7, simulated and experimental volume fraction data are arranged to show the deviation from the designed volume fraction, whose values for each dilution was calculated by applying the resistor combinations of Table 2 to the mixing laws presented in Table 1, for the R1 branch of each topology. Note that many of the experimental values for χ were found to be greater than those designed, resulting in a tendency for negative deviations. This seems to occur largely because the mean expected resistance for many elements is less than their designed value, reflected by an overall higher mean value for Δxy and Δz tolerance distribution (or w, L and h channel parameters).
Comparison of experimental mixing ratio deviation from designed mixing ratio in comparison to simulated mixing ratio deviation to designed mixing ratio.
For each graph, the upper and lower bound describe a 2σ deviation from the expected mixing ratio, such that the shaded region, effectively the simulated operating space, is established by the manufacturer tolerance that suggests 95% of the constructed resistor elements will fall within specification. Experimental data lie within the simulated operational working space for the (a) 2-inlet Fork Topology, (b) 3-inlet Fork Topology and (c) 3-inlet Ladder Topology.
This study effectively demonstrated that performance variations in microfluidic systems constructed using discrete elements could be statistically predicted in context of mass manufacturing. Device processing and network assembly level error propagation was simulated using empirically determined process parameters and mechanistic understanding of the SLA process. Figure 7 shows that the measurable performance of real circuits for parallel and serial mixing constructed from a sample component library reliably perform within virtually determined bounds of precision. These circuits were useful as a modular, adjustable and handheld laboratory tool for creating mixtures with very high levels of precision. Furthermore, the circuit topologies explored in this work are expandable to an arbitrary number of input solutions; the network and Monte Carlo analysis techniques presented here reliably enable the determination of performance of similar systems with scaled complexity.
Materials and Methods
Each circuit topology was tested manually by feeding the R1 branch of each circuit with a 0.34 M NaCl probe solution and running Milli-Q water through the remaining circuit branches. A syringe was connected at the output end and was manually retracted to prime the circuit branches with their respective solutions. After priming all branches, a clean syringe replaced the priming syringe and about 1 mL of diluted mixture was collected. In order to calculate the experimental volume fraction, an osmometer (Gonotec Osmomat 3000) was used to measure the osmolality of 0.5 mL of the mixed product. The stock NaCl solution had a measured osmolarity of  osmol-kg–1; a linear relationship between osmolarity and salt concentration was used to find the concentrations of the diluted mixtures. All components were fabricated through a contract manufacturer Fineline Prototyping (Protolabs Inc.) in Watershed 11122 XC photoresin material.
osmol-kg–1; a linear relationship between osmolarity and salt concentration was used to find the concentrations of the diluted mixtures. All components were fabricated through a contract manufacturer Fineline Prototyping (Protolabs Inc.) in Watershed 11122 XC photoresin material.
The Monte Carlo simulation was written in Python 3.4.2 using the Anaconda SciPy framework. Supplementary Figure 2 shows an overview of the procedure. Process data were collected (Supplementary Figure 1) and fit to a normal distribution, from which the standard deviation and mean values were used to find expected mean and tolerance values for all members of the resistor component library. A loop with a maximum count of 5000 tries was constructed, wherein a normally distributed pseudorandom number generator was called to create a kit of virtual resistors set by the expected values in the component library in the previous step. The kit was in turn used to calculate expected values for mixing laws, yielding a predicted χ value. The resulting χ values were compared to those expected from resistors with no manufacturing error, yielding the deviation from intended behavior expected from mass-manufactured parts.
Additional Information
How to cite this article: Bhargava, K. C. et al. Predicting the behavior of microfluidic circuits made from discrete elements. Sci. Rep. 5, 15609; doi: 10.1038/srep15609 (2015).
References
Au, A. K., Lee, W. & Folch, A. Mail-order microfluidics: evaluation of stereolithography for the production of microfluidic devices. Lab Chip 15, 1294–1301 (2014).
Lee, W. et al. 3D-Printed Microfluidic Device for the Detection of Pathogenic Bacteria Using Size-based Separation in Helical Channel with Trapezoid Cross-Section. Sci. Rep. 5, 7717 (2015).
Zhu, F. et al. Three-dimensional printed millifluidic devices for zebrafish embryo tests. Biomicrofluidics 9, 046502 (2015).
Au, A. K., Bhattacharjee, N., Horowitz, L. F., Chang, T. C. & Folch, A. 3D-printed microfluidic automation. Lab Chip 5, 1934–41 (2015).
Rogers, C. I., Qaderi, K., Woolley, A. T. & Nordin, G. P. 3D printed microfluidic devices with integrated valves. Biomicrofluidics 9, 016501 (2015).
Ho, C. M. B., Ng, S. H. G., Li, K. H. H. & Yoon, Y.-J. 3D Printed Microfluidics for Biological Applications. Lab Chip May (2015).
Bhargava, K. C., Thompson, B. & Malmstadt, N. Discrete elements for 3D microfluidics. Proc. Natl. Acad. Sci. 111, 15013–15018 (2014).
Bruus, H. Theoretical microfluidics (Oxford University Press, Oxford, 2008).
Fuerstman, M. J. et al. Solving mazes using microfluidic networks. Langmuir 19, 4714–4722 (2003).
Oh, K. W., Lee, K., Ahn, B. & Furlani, E. P. Design of pressure-driven microfluidic networks using electric circuit analogy. Lab Chip 12, 515 (2012).
Choi, S., Lee, M. G. & Parka, J. K. Microfluidic parallel circuit for measurement of hydraulic resistance. Biomicrofluidics 4, 1–9 (2010).
Sun, K., Wang, Z. & Jiang, X. Modular microfluidics for gradient generation. Lab Chip 8, 1536–1543 (2008).
Leslie, D. C. et al. Frequency-specific flow control in microfluidic circuits with passive elastomeric features. Nat. Phys. 5, 231–235 (2009).
Irimia, D., Geba, D. A. & Toner, M. Universal microfluidic gradient generator. Anal. Chem. 78, 3472–3477 (2006).
Yang, M., Yang, J., Li, C.-W. & Zhao, J. Generation of concentration gradient by controlled flow distribution and diffusive mixing in a microfluidic chip. Lab Chip 2, 158–163 (2002).
Lin, F. et al. Generation of dynamic temporal and spatial concentration gradients using microfluidic devices. Lab Chip 4, 164–167 (2004).
Dertinger, S. K. W., Chiu, D. T., Jeon, N. L. & Whitesides, G. M. Generation of Gradents Having Complex Shapes Using Microfluidic Networks. Anal. Chem. 73, 1240–1246 (2001).
Jacobson, S. C., McKnight, T. E. & Ramsey, J. M. Microfluidic devices for electrokinetically driven parallel and serial mixing. Anal. Chem. 71, 4455–4459 (1999).
Neils, C., Tyree, Z., Finlayson, B. & Folch, A. Combinatorial mixing of microfluidic streams. Lab Chip 4, 342–350 (2004).
Kim, C. et al. A serial dilution microfluidic device using a ladder network generating logarithmic or linear concentrations. Lab Chip 8, 473–9 (2008).
Acknowledgements
This work was supported by the National Institutes of Health (Award 1R01GM093279).
Author information
Authors and Affiliations
Contributions
K.C.B., B.T. and N.M. designed the research and wrote the main manuscript text. K.C.B. and B.T. prepared figures. K.C.B., B.T. and D.I. performed the research. K.C.B. and B.T. contributed equally to this work.
Ethics declarations
Competing interests
The microfluidic platform described herein is the subject of a US patent application filed by USC and ReoLab, Inc. Authors K.C.B., B.T. and N.M. are equity holders in ReoLab.
Electronic supplementary material
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Bhargava, K., Thompson, B., Iqbal, D. et al. Predicting the behavior of microfluidic circuits made from discrete elements. Sci Rep 5, 15609 (2015). https://doi.org/10.1038/srep15609
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep15609
This article is cited by
-
Impact of inertia and channel angles on flow distribution in microfluidic junctions
Microfluidics and Nanofluidics (2020)
-
Engineered hydrophobicity of discrete microfluidic elements for double emulsion generation
Microfluidics and Nanofluidics (2016)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.