Abstract
The developing human brain remains one of the few unsolved mysteries of science. Advancements in developmental biology, neuroscience and medical imaging have brought us closer than ever to understand brain development in health and disease. However, the precise role of mechanics throughout this process remains underestimated and poorly understood. Here we show that mechanical stretch plays a crucial role in brain development. Using the nonlinear field theories of mechanics supplemented by the theory of finite growth, we model the human brain as a living system with a morphogenetically growing outer surface and a stretch-driven growing inner core. This approach seamlessly integrates the two popular but competing hypotheses for cortical folding: axonal tension and differential growth. We calibrate our model using magnetic resonance images from very preterm neonates. Our model predicts that deviations in cortical growth and thickness induce morphological abnormalities. Using the gyrification index, the ratio between the total and exposed surface area, we demonstrate that these abnormalities agree with the classical pathologies of lissencephaly and polymicrogyria. Understanding the mechanisms of cortical folding in the developing human brain has direct implications in the diagnostics and treatment of neurological disorders, including epilepsy, schizophrenia and autism.
Similar content being viewed by others
Introduction
One of the most intriguing, unanswered questions of the 21st century is what drives the formation of folds during human brain development. Fig. 1 illustrates the folding pattern of the human brain, which plays a significant role in health and disease: Recent research has, for example, revealed a positive correlation between cortical gyrification and intelligence1. Beyond that, the surface morphology is associated with malformations, like lissencephaly2 and polymicrogyria3 and with neurological disorders, like schizophrenia4,5 and autism6,7. These structural abnormalities originate from early in utero development8 and may give rise to functional pathologies like developmental delay, refractory epilepsy and cerebral palsy9. Rapid advancements in medical imaging provide tremendous opportunities to better understand brain development: They enable the quantitative classification of malformations10 and allow us to scan preterm brains in which folding is still incomplete8. Yet, despite significant progress throughout the past decade, the underlying mechanisms of brain folding remain largely unknown.
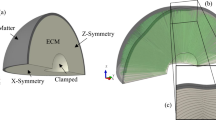
Schematic illustration of the human brain.
The cross section of the brain illustrates its characteristic convoluted surface with ridges called gyri and grooves called sulci. The outer layer of gray matter, which forms the cortex, is made up of neuronal cell bodies including the cell nuclei. The inner core of white matter, which forms the subcortex, consists primarily of neuronal axons. Cortical folding maximizes the surface-to-volume ratio to increase the number of nuclei and decrease the relative distance between them.
Historically, human brain development has been studied using a merely observational approach11, mainly on the basis of genetics and cytology. Recent evidence suggests that the mechanical microenvironment plays a crucial role in controlling pattern formation12. In this regulatory process, mechanics and biology are coupled bi-directionally: On the one hand, the biological microstructure changes in response to mechanical loading; On the other hand, the mechanical parameters change in response to biological processes13. Here we study human brain development using a fully coupled biomechanical approach to provide a holistic and predictive understanding of the mechanobiology of gyrogenesis.
The popular hypothesis that axons pull on the cortex to initiate cortical folding14 has recently been questioned and disproven experimentally15. Current studies based on magnetic resonance imaging now suggest that differential growth16 - with a faster growing surface layer and slower growing inner core - drives the formation of cortical folds17. From other organ systems like the airway18, the intestine19 and the gut20, but also from plants21 and seashells22, we know that differential growth can generate sufficient compressive residual stresses to induce structural instabilities such as buckles, folds, or creases23, even in the absence of external loading24. It seems intuitive to hypothesize that differential growth - with a faster growing cortex and slower growing subcortex - also plays a major role during brain development.
In this study, we establish a mechanical model for differential growth to simulate cortical folding in the developing human brain. The key challenge is to identify evolution equations of growth that realistically mimic the underlying biochemical processes25,26. In the simplest case, growth is purely morphogenetic, evolving in time irrespective of the mechanical environment11. In more complex cases, growth is mechanically driven, for instance by hypertension in arteries27 or by hyperstretch in skin28. In our model, the cortex, the outer surface of the brain, grows morphogenetically at a constant rate, while the subcortex, the inner core, grows in response to overstretch. Subcortical growth thus mimics the phenomenon of towed growth29,30, the chronic elongation of axons when stretched beyond their physiological limit31,32.
We hypothesize that morphological abnormalities in the human brain originate from misbalanced cortical and subcortical growth. Our rationale is that mechanically-driven growth has recently been shown to explain gyral wavelengths33 and stress patterns15 in the developing ferret brain. Based on these findings, we reveal mechanisms that cause abnormal brain folding and correlate our results with characteristic pathologic observations in lissencephalic, polymicrogyric and schizophrenic brains8. Identifying which parameters affect gyrogenesis and surface morphology can provide a tremendous insight into the human brain - how it forms and how it functions.
Results
Development of brain surface morphology
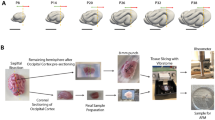
In the human brain, cortical folding takes place primarily in utero, during 24 and 32 weeks of gestation. In preterm infants, cortical folding is incomplete at birth, which allows us to explore the evolution of folding patterns using standard medical imaging techniques. Fig. 2 contrasts magnetic resonance images and simulated brain slices of the developing human brain in very preterm neonates at 27, 29 and 32 weeks of gestation. The magnetic resonance images (Fig. 2a) were acquired as part of a four-year prospective neuroimaging study of very preterm neonates after receiving informed, written consent from the parents. The study was approved by the Research Ethics Committee8. The magnetic resonance images reveal the spatio-temporal evolution of the characteristic convoluted surface morphology. Close ups of the blue rectangular cross section (Fig. 2b) illustrate progressive cortical growth associated with an increase in sulcal depth. The simulated brain slices (Fig. 2c) are based on a finite element model of cortical and subcortical growth. The underlying continuum model, its finite element discretization and the chosen parameters are specified in detail in the Methods section. The simulated brain slices display the progression of growth: At week 27, the cortex has increased 65% in volume and shallow sulci begin to form; At week 29, the cortex has increased 76% in volume and sulci become more prominent; At week 32, the cortex has doubled its volume, sulci increase significantly in depth and gyri begin to form first self-contact. The simulations predict the characteristic features of the developing human brain: gyrogenesis and progressive cortical folding between 27 and 32 weeks of gestation (Fig. 2c).
Development of brain surface morphology.
(a) Magnetic resonance images of the developing human brain in very preterm neonates at 27, 29 and 32 weeks of gestation display the evolution of the characteristic convoluted surface morphology. The blue rectangle frames the two-dimensional rectangular domain for the simulation. (b) Close ups of the simulated domain display a progressive increase in sulcal depth until the gyri form first self-contact. (c) Simulated morphologies of developing human brain section at 27, 29 and 32 weeks of gestation display a gradual increase in cortical volume associated with progressive gyrification.
Effect of cortical growth rate on surface morphology
Cortical growth depends on various biological processes like cellular differentiation, growth, proliferation and migration. Not surprisingly, it varies significantly both in space and time. Fig. 3 illustrates the effect of varying cortical growth rates on growth, elastic volume stretch, gyral wavelength and gyrification index as predicted by our model. For cortical growth rates below a critical value, subcortical growth is fast enough to compensate for cortical growth: Gyrification is suppressed and the surface remains smooth. Increasing the cortical growth rate beyond this critical value decreases the relative amount of subcortical growth (Fig. 3a), which increases the elastic volume stretch (Fig. 3b). Although the wavelength remains almost unaffected by this change (Fig. 3c), the reduced relative subcortical growth reduces the depth of the individual sulci, which decreases the gyrification index (Fig. 3d). In summary, with increasing cortical growth rate, folds maintain their length, but become more shallow.
Effect of cortical growth rate on surface morphology.
Sensitivity of (a) growth  , (b) elastic volume stretch Je, (c) gyral wavelength λ and (d) gyrification index GI for varying cortical growth rates Gc. For cortical growth rates below a critical value, no gyrification occurs. Increasing the cortical growth rate beyond this value does not affect the gyral wavelength but decreases the gyrification index: Folds maintain their length, but become more shallow.
, (b) elastic volume stretch Je, (c) gyral wavelength λ and (d) gyrification index GI for varying cortical growth rates Gc. For cortical growth rates below a critical value, no gyrification occurs. Increasing the cortical growth rate beyond this value does not affect the gyral wavelength but decreases the gyrification index: Folds maintain their length, but become more shallow.
Effect of initial cortical thickness on surface morphology
The initial thickness of the cortical surface varies significantly throughout the human brain. Fig. 4 illustrates the effect of thickness variation on growth, elastic volume stretch, gyral wavelength and gyrification index as predicted by our model. Increasing the initial cortical thickness decreases the amount of growth in both cortex and subcortex (Fig. 4a). Reduced cortical growth results in less localized deformation patterns, reduced axonal tension in the subcortex and reduced subcortical growth. Increasing the initial cortical thickness affects the elastic volume stretch only marginally (Fig. 4b). However, it markedly stiffens the cortical surface, which increases the gyral wavelength (Fig. 4c) and decreases the gyrification index (Fig. 4d). In summary, with increasing initial cortical thickness, folds become longer and more shallow.
Effect of initial cortical thickness on surface morphology.
Sensitivity of (a) growth  , (b) elastic volume stretch Je, (c) gyral wavelength λ and (d) gyrification index GI for varying initial cortical thickness tc. Increasing the initial cortical thickness increases the gyral wavelength and decreases the gyrification index: Folds become longer and more shallow.
, (b) elastic volume stretch Je, (c) gyral wavelength λ and (d) gyrification index GI for varying initial cortical thickness tc. Increasing the initial cortical thickness increases the gyral wavelength and decreases the gyrification index: Folds become longer and more shallow.
Lissencephaly
Lissencephaly is a rare malformation of the human brain associated with migration disorders and a poorly convoluted cortex9. During neuronal migration, a significant fraction of neurons fails to reach the outer cortex and remains underneath the cortical plate. Neuronal misplacement results in a severe defect of cortical connectivity and a markedly thickened cortex. Fig. 5 illustrates the pathology and simulation of a lissencephalic brain. Magnetic resonance images reveal an increased cortical thickness associated with a decrease in depth and number of gyri and sulci and a decreased subcortical volume (Fig. 5a). Simulations of moderately and severely increased cortical thicknesses display the characteristic morphological abnormalities of lissencephalic brains: the formation of a few shallow gyri (Fig. 5b) and the complete suppression of gyrification (Fig. 5c).
Pathology and simulation of lissencephaly.
(a) Magnetic resonance images of a lissencephalic brain display an increase in cortical thickness, a decrease in depth and number of cortical gyri and sulci and a decrease in subcortical volume. (b), (c) Simulated morphologies for a moderately and severely increased cortical thickness display the formation of a single shallow gyrus and the complete suppression of gyrification.
Polymicrogyria
Polymicrogyria is a malformation of the human brain associated with organization disorders and an overly convoluted cortex9. At inspection, the polymicrogyric brain surface appears smooth with only a few aberrant sulci. Cutting the brain exposes the characteristic convoluted structure with an increased number of secondary folds. Fig. 6 illustrates the pathology and simulation of a polymicrogyric brain. Magnetic resonance images reveal a reduced cortical thickness associated with an increase in number and a decrease in size of gyri and sulci. (Fig. 6a). Simulations of a reduced cortical thickness combined with physiological and severely retarded subcortical growth display the characteristic morphological abnormalities of mircogyric brains: the formation of numerous small gyri and sulci (Fig. 6b) and the formation of secondary folds (Fig. 6c).
Pathology and simulation of polymicrogyria.
(a) Magnetic resonance images of a polymicrogyric brain display a reduced cortical thickness, an increase in number and a decrease in size of gyri and sulci. (b), (c) Simulated morphologies for severely reduced cortical thickness at physiological and severely reduced subcortical growth rates display increased gyrification without and with formation of secondary folds.
Schizophrenia
Schizophrenia is a mental disorder with symptoms like delusions, social withdrawal and disorganized thinking associated with regional structural abnormalities in the brain. Fig. 7 contrasts the pathology and simulation of a healthy and a schizophrenic brain. Surface reconstructions reveal regional structural differences in the color-coded regions34. In comparison with the healthy brain (Fig. 7a), the schizophrenic brain displays a locally reduced cortical thickness and a locally increased gyrification index (Fig. 7b). Simulations of a reduced cortical thickness in the blue rectangular cross-section of the superior temporal gyrus display the characteristic morphological abnormalities of schizophrenic brains: the regional increase of the gyrification index from 1.47 in the healthy brain (Fig. 7c) to 1.71 in the schizophrenic brain (Fig. 7d).
Pathology and simulation of schizophrenia.
(a), (b) Surface reconstructions of healthy and schizophrenic brain display a reduced cortical thickness and an increase in number and depth of gyri and sulci in the color-coded regions of schizophrenic brains, adopted with permission from34. (c), (d) Simulated morphologies in blue rectangular cross-section through the superior temporal gyrus at physiological and reduced cortical thickness display an increase in number and depth of gyri and sulci associated with an increased gyrification index.
Discussion
Mechanics plays a critical role in brain development
Brain development was long considered an exclusively morphogenetic process, independent of forces, stress, stretch, or strain. There is now increasing evidence that mechanics plays a significantly role in regulating brain morphology. Here we have explored the role of mechanical stretch in human brain development using the nonlinear field theories of mechanics supplemented by the theory of finite growth. This allowed us to bridge the scales and correlate subcellular and cellular events like axon elongation to clinically relevant characteristics like surface area and gyrification indices.
The competing hypotheses of axonal tension and differential growth are not mutually exclusive
Mechanical factors are recognized as potential driving force for cortical folding, but controversies around two competing hypotheses, axonal tension and differential growth, have slowed down further progress35. Axonal tension, a mechanism to bring functionally related units topographically close together14, disagrees with dissection experiments, which confirm the general existence of axonal tension, however, not along the predicted directions15. Differential growth, a mechanism to release residual stresses by surface buckling16, agrees with stress distributions in dissection experiments, however, not with physiologically realistic stiffness ratios35. Here we combine both mechanisms in a unified model with a morphogenetically growing outer surface36 and stretch-driven growing inner core28. This allows us to predict both axonal tension, in the form of the elastic volume stretch Je and differential growth, in the form of cortical and subcortical volume growth  and
and  .
.
Cortical growth induces extreme subcortical deformation and axonal stretch
There is a general agreement that cortical growth is almost entirely morphogenetic, independent of mechanical factors17. We know, however, that rapidly growing biological membranes like the cortex may induce mechanical instabilities24, associated with large deformations of the overall system36. In the ferret, cortical growth is as rapid as 12.7 mm2/day per hemisphere in the third week after birth and even increases to 36.7 mm2/day per hemisphere in the fourth week37. In humans, cortical growth is on the order of  in first year after birth and decays towards
in first year after birth and decays towards  in the second year38. Not surprisingly, this creates extreme subcortical deformation, which our model captures in the form of the elastic volume stretch Je. Fig. 3 illustrates this effect through an increasing elastic volume stretch Je in response to increasing cortical growth rates Gc.
in the second year38. Not surprisingly, this creates extreme subcortical deformation, which our model captures in the form of the elastic volume stretch Je. Fig. 3 illustrates this effect through an increasing elastic volume stretch Je in response to increasing cortical growth rates Gc.
Subcortical growth is a result of stretch-driven axon elongation
On the cellular level, chronic axonal overstretch activates mechanotransduction pathways, which collectively result in a gradual increase in axonal length31. In the blue whale, axonal growth can be as rapid as 3 cm/day, in the giraffe up to 2 cm/day. In humans, maximum axonal growth in utero can be up to 11 cm/month during peak growth around the fifth months of gestation30. In vitro, under extreme conditions, axons tolerate elongation rates of up to 8 mm/day towards a total growth of 10 cm39. On the subcellular level, axonal growth is associated with an increase in the number of microtubules and neurofilaments, an increase in cytoplasm and an increase in plasma membrane, while the ultrastructural appearance and the diameter of the growing axon remain virtually unchanged39. Axonal growth is a self-regulating mechanism: As the axon grows, it reduces its stretch and thereby regulates its length30. These phenomena are collectively known as towed growth, the chronic axon elongation in response to mechanical stimuli29. While initial axon elongation experiments use tension as mechanical stimulus30, recent experiments prefer to use stretch instead40. Since stretch-driven growth is purely kinematic, it is easier to control and manipulate experimentally39. In our model, we suggest stretch rather than tension33 as the driving mechanism for subcortical growth. Our model inherently captures the self-regulating mechanism of growth by activating axon elongation only if the elastic volume stretch Je chronically exceeds the physiological limit J041.
Misbalanced cortical and subcortical growth creates morphological abnormalities
Our results confirm our hypothesis that morphological abnormalities in the human brain originate from misbalanced cortical and subcortical growth: Abnormally slowly growing cortices allow axons to almost instantaneously respond to growth-induced subcortical deformation so that no folds emerge (Fig. 3, left); Physiologically growing cortices create sufficient subcortical deformation to trigger axon elongation and subcortical growth (Fig. 3, middle); Abnormally fast growing cortices reduce the sulcal depth, decrease the gyrification index (Fig. 3, right) and provoke the formation of secondary folds12 (Fig. 6, right). These findings agree with qualitative observations in diseased human brains16: Lissencephalic brains, characterized by a poorly convoluted morphology (Fig. 5a) display reduced growth in the cortical layer (Figs. 5b,c); Polymicrogyric brains, characterized by an overly convoluted morphology (Fig. 6a) display reduced growth in the subcortical layer (Figs. 6b,c).
Our results further demonstrate that morphological abnormalities in the human brain could also originate from misbalanced cortical and subcortical thicknesses: Abnormally thin cortices grow at higher wavelengths with increased gyrification indices (Fig. 4, left); Abnormally thick cortices grow at lower wavelengths with decreased gyrification indices (Fig. 4, right). In agreement with the literature18,33, our simulations suggest that the gyral wavelength increases with cortical thickness. Severely thickened cortices may even suppress the formation of folds entirely (Fig. 5, right). These trends are consistent with the pathology of diseased human brains42: Lissencephalic brains, characterized by a thick cortex (Fig. 5a) display a smooth surface (Figs. 5b,c); Polymicrogyric brains, characterized by a thin cortex (Fig. 5a) display a large number of small folds (Figs. 5b,c). Future studies of developing malformations in preterm infants would be desirable to reveal whether an abnormal cortical thickness is a cause or consequence of the disease.
Our simulated quantitative metrics for brain surface morphology, gyral wavelengths and gyrification indices, agree well with reported values in the literature. Our wavelengths range from λ = 3.5 mm to λ = 10.3 mm (Figs. 3,4), which is consistent with the clinically measured intersulcal distance of λ = 8.5 mm at the end of the seventh month of gestation16. Our gyrification indices take values up to 1.9 (Figs. 3,4,7), which is slightly lower than characteristic gyrification indices in healthy human brains of 2.5 to 3.043. We attribute these discrepancies to our simplified simulation domain and to the uniformity of our folding pattern. Yet, the tendency of increased gyrification44 in regions with reduced cortical thickness45 in schizophrenic brains is consistent with our simulation.
Our current model has a few spatial and temporal limitations
Spatially, our most relevant limitation is isotropic volumetric growth46: In the cortex, we could refine volumetric growth as the collective result of two independent mechanisms, surface growth and surface thickening16. In the subcortex, we could refine growth as transversely isotropic, based on regionally varying axon orientation maps33. Anisotropic growth would introduce less regular, more directionally oriented gyri and sulci, which would agree more closely with the magnetic resonance images of human brains (Figs. 2,5,6,7). With only minor modifications, we could also model individual laminar growth rates across the cortical thickness42 and individual regional growth rates across the cortical surface47. Temporally, our most relevant limitation is associated with constant growth rates: Late neuronal migration, positive growth, takes place in the outer cortical layers to form gyri, while neuronal apoptosis, negative growth, takes place in the inner layers to form sulci48,49. The outer layers contain sensory and associative neurons, which receive many axon collaterals, while the inner layers contain mainly projection neurons, which send one axon each50,51. To functionally link these cellular and molecular events to cortical and subcortical growth37, we could turn different growth rates on and off to mimic the sequence of events during gyrogenesis, including neuronal proliferation, differentiation, apoptosis, dendrogenesis, synapsogenesis, glial proliferation, lamination and cellular rearrangement9.
Relevance of mechanics in human brain development
We have established a mechanical model to explain cortical folding in the developing human brain. This proof of concept might have to undergo a few refinements, but ultimately, it may help us to address basic scientific questions on different scales: On the patient scale, can we identify candidates at risk for neurological disorders and if so, how can we quantify the level of risk? On the organ scale, is there a general pattern of gyrogenesis for different evolutionary lineages and if so, how is it correlated to growth and cortical thickness? On the tissue scale, is there a biological limit for gyral lengths and if so, what are its key contributors? On the cellular scale, what are the rate limiting factors for growth and if any, how can we manipulate them? Bridging the scales, is there a correlation between axonal metabolism and the energy of growth and if so, what is the efficiency index of the living system? Ultimately, collectively answering these questions may bring us closer to answer the key clinically question in brain development: How do we systematically manipulate brain surface morphologies through pharmacologic or therapeutic treatment?
Conclusion
A mechanical model for brain development can explain variations in gyral wavelengths and gyrification indices of healthy and diseased human brains. A misbalance in cortical and subcortical growth or thickness causes morphological abnormalities: A slower growing or thinner cortex generally enhances folding and increases the gyrification index; A faster growing or thicker cortex reduces folding and decreases the gyrification index. These characteristics are in excellent agreement with the classical pathologies of lissencephaly and polymicrogyria. Understanding the mechanisms of cortical folding in the developing human brain has direct implications on the diagnostics and treatment of neurological disorders, including severe retardation, epilepsy, schizophrenia and autism.
Methods
Continuum model for cortical and subcortical growth
Fig. 8 illustrates our model for cortical and subcortical growth in the developing human brain. We model growth using the nonlinear field theories of mechanics supplemented by the theory of finite growth52. This results in a set of five equations, which define kinematics, constitutive behavior, mechanical equilibrium, growth kinematics and growth kinetics.
Continuum model for cortical and subcortical growth.
The cortex, the gray matter, grows morphogenetically at a constant rate Gc. Cortical growth induces subcortical deformation, which triggers subcortical growth. The subcortex, the white matter, grows at a stretch-dependent rate as Gs(Je − J0), where Gs mimics the axon elongation rate and Je − J0 activates growth only, if the elastic volume stretch Je exceeds its baseline value J0. The subcortical volume growth  mimics the three-dimensional effect of chronic axon elongation
mimics the three-dimensional effect of chronic axon elongation  , which is activated when axons are stretched beyond their physiological limit.
, which is activated when axons are stretched beyond their physiological limit.
Kinematically, we decompose the deformation gradient F, the spatial gradient of the nonlinear deformation map, into an elastic contribution Fe and a growth contribution Fg,

Similarly, we decompose the overall volume change J = JeJg = det(F) into an elastic volume change Je = det(Fe) and a growth-induced volume change Jg = det(Fg). Constitutively, only the elastic contribution Fe generates stresses41,

where λ and μ are the elastic Lamé constants, I is the second order unit tensor and Fet is the transpose of Fe. These stresses enter the mechanical equilibrium equation

which we solve numerically using the finite element method. To close the set of governing equations, we constitutively prescribe the evolution of growth. Kinematically, we assume that growth is purely isotropic,

This implies that the growth volume  is equivalent to the growth multiplier
is equivalent to the growth multiplier  to the power of three. Kinetically, we hypothesize that cortical growth is purely morphogenetic and that subcortical growth is stretch-induced,
to the power of three. Kinetically, we hypothesize that cortical growth is purely morphogenetic and that subcortical growth is stretch-induced,

where Gc and Gs are the cortical and subcortical growth rates. We assume that the subcortex is primarily populated by axons and correlate its growth rate with the experimentally well-characterized axon elongation rate30,39. In contrast to cortical growth, subcortical growth is activated only, if the elastic volume stretch Je exceeds its baseline value J0, i.e., when axons are stretched beyond their physiological limit31,53.
Finite element model for cortical folding
To simulate cortical folding, we create a finite element model of a two-dimensional rectangular subsection of a human brain slice. Fig. 2 illustrates the simulation domain, which is 2 cm long, 1 cm wide and 0.05 cm thick, discretized by a total of 80 × 40 × 1 = 3, 200 tri-linear Q1 elements and 19,926 degrees of freedom. We assume a plane strain state and fix the left, bottom and right boundary nodes orthogonal to the boundary, but allow them to slide freely along the corresponding edge. We model the cortex as Neo Hookean elastic with a Young's modulus Ec = 9, 210.87 Pa and a Poisson's ratio νc = 0.458, corresponding to Lamé constants λc = 34, 335 Pa and μc = 3, 159 Pa54. We assume that the cortex is three times stiffer than the subcortex, which we model as Neo Hookean elastic with Lamé constants λs = 11, 482 Pa and μs = 1, 053 Pa. We choose the initial cortical thickness to tc = 0.75 mm, the cortical growth rate to Gc = 2.0, the subcortical growth rate to Gs = 0.003 and the physiological limit to J0 = 153. We solve the resulting nonlinear finite element equations using a standard Newton-Raphson method36.
Gyrificaiton index to quantify cortical folding
Fig. 9 illustrates a common clinical metric to quantify the degree of cortical folding, the gyrification index. The gyrification index is the ratio between the complete cortical contour length and the outer cortical contour length. In humans, it increases during ontogenesis from the smooth initial brain surface with values close to 1.0 towards the heavily convoluted adult brain surface with values between 2.5 and 3.043. Lissencephalic brains have smaller gyrification indices2; Polymicrogyric brains have larger gyrification indices3. To quantify the degree of cortical folding for varying cortical growth rates and varying cortical thicknesses, we determine the gyrification index semi-automatically by contour tracing.
Gyrificaiton index to quantify cortical folding.
The gyrification index is the ratio between the complete cortical contour length, solid line and the outer cortical contour length, dashed line. It is used to quantify the degree of cortical folding and can be determined semi-automatically by contour tracing.
References
Luders, E. et al. Mapping the relationship between cortical convolution and intelligence: Effects of gender. Cereb. Cortex 18, 2019–2026 (2008).
Landrieu, P., Husson, B., Pariente, D. & Lacroix, C. MRI-neuropathological correlations in type 1 lissencephaly. Neuroradiology 40, 173–176 (1998).
Tortori-Donati, P. & Rossi, A. Brain malformations. In: Pediatric Neuroradiology, 71–198, Springer Berlin Heidelberg (2005).
Harrison, P. J. The neuropathology of schizophrenia a critical review of the data and their interpretation. Brain 122, 593–624 (1999).
Jou, R. J., Hardan, A. Y. & Keshavan, M. S. Reduced cortical folding in individuals at high risk for schizophrenia: A pilot study. Schizophrenia Res. 75, 309–313 (2005).
Hardan, A. Y., Jou, R. J., Keshavan, M. S., Varma, R. & Minshew, N. J. Increased frontal cortical folding in autism: A preliminary MRI study. Psychiatr. Res. Neuroimag. 131, 263–268 (2004).
Nordahl, C. W. et al. Cortical folding abnormalities in autism revealed by surface-based morphometry. J. Neurosc. 27, 11725–11735 (2007).
Raybaud, C., Ahmad, T., Rastegar, N., Shroff, M. & Al Nassar, M. The premature brain: Developmental and lesional anatomy. Neuroradiology 55, S23–S40 (2013).
Raybaud, C. & Widjaja, E. Development and dysgenesis of the cerebral cortex: Malformations of cortical development. Neuroimag. Clin. N. Am. 21, 483–543 (2011).
Raybaud, C., Girald, N., Canto-Moreira, N. & Poncet, M. High-definition magnetic resonance imaging identification of cortical dysplasias: micropolygyria versus lissencephaly. Dysplasias of cerebral cortex and epilepsy. Guerrini, R. et al. (eds.) Lippincott-Raven, Philadelphia, 1996.
Menzel, A. & Kuhl, E. Frontiers in growth and remodeling. Mech. Res. Comm. 42, 1–14 (2012).
Li, B., Cao, Y.-P., Feng, X.-Q. & Gao, H. Mechanics of morphological instabilities and surface wrinkling in soft materials: A review. Soft Matter 8, 5728–5745 (2012).
Kuhl, E. Growing matter - A review of growth in living systems. J. Mech. Beh. Biomed. Mat. 29, 529–543 (2014).
Van Essen, D. C. A tension-based theory of morphogenesis and compact wiring in the central nervous system. Nature 385, 313–318 (1997).
Xu, G. et al. Axons pull on the brain, but tension does not drive cortical folding. J. Biomech. Eng. 132, 071013 (2010).
Richman, D. P., Stewart, R. M., Hutchinson, J. W. & Caviness, V. S. Mechanical model of brain convolutional development. Science 189, 18–21 (1975).
Ronan, L. et al. Differential tangential expansion as a mechanism for cortical gyrification. Cereb. Cortex 10.1093/cercor/bht082 (2013).
Eskandari, M., Pfaller, M. R. & Kuhl, E. On the role of mechanics in chronic lung disease. Materials 6, 5639–5658 (2013).
Ben Amar, M. & Jia, F. Anisotropic growth shapes intestinal tissues during embryogenesis. Proc. Nat. Acad. Sci. 110, 10525–10530 (2013).
Savin, T. et al. On the growth and form of the gut. Nature 476, 57–63 (2011).
Harrington, M. J. et al. Origami-like unfolding of hydro-actuated ice plant seed capsules. Nature Comm. 2, 337 (2011).
Chirat, R., Moulton, D. E. & Goriely, A. Mechanical basis of morphogenesis and convergent evolution of spiny seashells. Proc. Nat. Acad. Sci. 110, 6015–6020 (2013).
Jin, L., Cai, S. & Suo, Z. Creases in soft tissues generated by growth. Eur. Phys. Lett. 95, 64002 (2011).
Goriely, A. & Ben Amar, M. Differential growth and instabilities in elastic shells. Phys. Rev. Lett. 94, 198103 (2005).
Ambrosi, D. et al. Perspectives on biological growth and remodeling. J. Mech. Phys. Solids 59, 863–883 (2011).
Dunlop, J. W. C., Fischer, F. D., Gamsjäger, E. & Fratzl, P. A theoretical model for tissue growth in confined geometries. J. Mech. Phys. Solids 58, 1073–1087 (2010).
Kuhl, E., Maas, R., Himpel, G. & Menzel, A. Computational modeling of arterial wall growth. Biomech. Model. Mechanobio. 6, 321–331 (2007).
Buganza Tepole, A., Ploch, C. J., Wong, J., Gosain, A. K. & Kuhl, E. Growing skin: A computational model for skin expansion in reconstructive surgery. J. Mech. Phys. Solids 59, 2177–2190 (2011).
Weiss, P. Nerve patterns: The mechanics of nerve growth. Growth, Third Growth Symp. 5, 163–203 (1941).
Bray, D. Axonal growth in response to experimentally applied mechanical tension. Dev. Bio. 102, 379–389 (1984).
Dennerll, T. J., Lamoureux, P., Buxbaum, R. E. & Heidemann, S. R. The cytomechanics of axonal elongation and retraction. J. Cell Bio. 109, 3073–3083 (1989).
Suter, D. M. & Miller, K. E. The emerging role of forces in axonal elongation. Prog. Neurobiol. 94, 91–101 (2011).
Bayly, P. V., Okamoto, R., Xu, G., Shi, Y. & Taber, L. A. A cortical folding model incorporating stress-dependent growth explains gyral wavelengths and stress patterns in the developing brain. Phys. Bio. 10, 016005 (2013).
Wisco, J. J. et al. Abnormal cortical folding patterns within Broca's area in schizophrenia: evidence from structural MRI. Schizophrenia Res. 94, 317–327 (2007).
Bayly, P. V., Taber, L. A. & Kroenke, C. D. Mechanical forces in cerebral cortical folding: A review of measurements and models. J. Mech. Beh. Biomed. Mat. 29, 568–581 (2014).
Papastavrou, A., Steinmann, P. & Kuhl, E. On the mechanics of continua with boundary energies and growing surfaces. J. Mech. Phys. Solids 61, 1446–1463 (2013).
Knutsen, A. K., Kroenke, C. D., Chang, Y. V., Taber, L. A. & Bayly, P. V. Spatial and temporal variations of cortical growth during gyrogenesis in the developing ferret brain. Cereb. Cortex 23, 488–498 (2013).
Li, G. et al. Mapping region-specific longitudinal cortical surface expansion from birth to 2 years of age. Cereb. Cortex 23, 2724–2733 (2013).
Pfister, B. J., Iwata, A. Meaney, D. F. & Smith, D. H. Extreme stretch growth of integrated axons. J. Neurosc. 2004, 7978–7983 (2004).
Smith, D. H. Stretch growth of integrated axon tracts: Extremes and exploitations. Prog. Neurobio. 89, 231–239 (2009).
Zöllner, A. M., Buganza Tepole, A. & Kuhl, E. On the biomechanics and mechanobiology of stretched skin. J. Theor. Bio. 297, 166–175 (2012).
Welker, W. Why does cerebral cortex fissure and fold? A review of determinants of gyri and sulci. Cerebral Cortex. Jones, E. G. & Peters, A. (eds.) Vol. 8B, Springer, New York, 1990.
Zilles, K., Armstrong, E., Schleicher, A. & Kretschmann, H.-J. The human pattern of gyrification in the cerebral cortex. Anat. Embryol. 179, 173–179 (1988).
Harris, J. M. et al. Gyrification in first-episode schizophrenia: A morphometric study. Bio. Psych. 55, 141–147 (2004).
Palaniyappan, L. & Liddle, P. F. Aberrant cortical gyrification in schizophrenia: a surface-based morphometry study. J. Psych. Neurosci. 37, 399–406 (2012).
Smart, I. H. M. & McSherry, G. M. Gyrus formation in the cerebral cortex of the ferret. II. Description of the internal histological changes. J Anat. 147, 27–43 (1986).
Hager, R., Lu, L., Rosen, G. D. & Williams, R. W. Genetic architecture supports mosaic brain evolution and independent brain-body size regulation. Nature Comm. 3, 1038 (2012).
Ferrer, I., Hernandez-Marti, M., Bernet, E. & Galofre, E. Formation and growth of the cerebral convolutions. I. Postnatal development of the median-suprasylvian gyrus and adjoining sulci in the cat. J. Anat. 160, 89–100 (1988).
Ferrer, I., Hernandez-Marti, M., Bernet, E. & Calopa, M. Formation and growth of the cerebral convolutions. II. Cell death in the suprasylvius gyrus and adjoining sulci in the cat. Dev. Brain Res. 45, 303–308 (1989).
Marin-Padilla, M. Prenatal and early postnatal ontogenesis of the human motor cortex: A Golgi study. I. The sequential development of the cortical layers. Brain Res. 23, 167–183 (1970).
Kostovic, I. & Jovanov-Milosevic, N. The development of the cerebral connections during the first 20-45 weeks of gestation. Sem. Fet. Neonat. Med. 11, 415–422 (2006).
Rodriguez, E. K., Hoger, A. & McCulloch, A. D. Stress-dependent finite growth in soft elastic tissues. J. Biomech. 27, 455–467 (1994).
Chada, S., Lamoureux, P., Buxbaum, R. E. & Heidemann, S. R. Cytomechanics of neurite outgrowth from chick brain neurons. J. Cell Science 110, 1179–1186 (1997).
Soza, G. et al. Determination of the elastic parameters of brain tissue with combined simulation and registration. Int. J. Med. Robot. Comp. Assist. Surg. 1, 87–95 (2005).
Acknowledgements
This work was supported by the National Science Foundation CAREER Award CMMI 0952021 and the INSPIRE Grant 1233054 and by the National Institutes of Health Grant U54 GM072970 to E.K.
Author information
Authors and Affiliations
Contributions
S.B. and E.K. designed the research, C.R. provided medical images, E.K. designed computational tools, S.B. performed simulations and analyzed data, S.B., C.R. and E.K. wrote the paper. All authors discussed results and commented on the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License. The images or other third party material in this article are included in the article's Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder in order to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/4.0/
About this article
Cite this article
Budday, S., Raybaud, C. & Kuhl, E. A mechanical model predicts morphological abnormalities in the developing human brain. Sci Rep 4, 5644 (2014). https://doi.org/10.1038/srep05644
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep05644
This article is cited by
-
Mechanical hierarchy in the formation and modulation of cortical folding patterns
Scientific Reports (2023)
-
Multi-scale measurement of stiffness in the developing ferret brain
Scientific Reports (2023)
-
Analysis of the compressible, isotropic, neo-Hookean hyperelastic model
Meccanica (2023)
-
Mathematical models of neuronal growth
Biomechanics and Modeling in Mechanobiology (2022)
-
PDE-constrained shape registration to characterize biological growth and morphogenesis from imaging data
Engineering with Computers (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.