Abstract
The scattering of a single photon with sufficiently high energy can cause a recoil of a motional scatterer. We study its backaction on the photon's coherent transport in one dimension by modeling the motional scatterer as a two-level system, which is trapped in a harmonic potential. While the reflection spectrum is of a single peak in the Lamb-Dicke limit, multi-peaks due to phonon excitations can be observed in the reflection spectrum as the trap becomes looser or the mass of the two-level system becomes smaller.
Similar content being viewed by others
Introduction
To realize all-optical devices at the single photon level for quantum information processing, it is very crucial to control the coherent transport of a single photon in some artificial quantum architectures. Recent theoretical studies1,2 have demonstrated that, in one dimension (1D), a fixed two-level system (TLS) can well serve this purpose in principle, since the interference between the spontaneously emitted photon and the incident one can result in a perfect reflection on resonance. Therefore, the TLS can act as a quantum node to function as a quantum optical switch and a single photon transistor3,4,5,6,7,8,9,10,11. Here, we emphasize that this observation is made only for the situation, in which the TLS is fixed and thus does not recoil in the scattering process.
However, when the energy of the single photon becomes comparable to the motional energy of the TLS, the recoil of the TLS caused by the incident photon becomes evident. It is obvious that such a backaction will have effect on the absorption and emission of photons. For instance, the energy of the gamma-ray photon emitted by a nucleus at rest is lower than the transition energy of the nucleus, while that absorbed by a nucleus at rest is higher than the transition energy of the nucleus, because in both emission and absorption processes energy is lost into the recoil motion of the nucleus12. In an ensemble of free nuclei, the energy shift is so great that the emission and absorption spectra have no overlap. As a result, the nuclear resonance fluorescence cannot happen in free nuclei.
In contrast, for nuclei bound in a solid crystal, there exist recoil-free emission and absorption and in consequence the nuclear resonance fluorescence can be observed. This phenomena is called the Mössbauer effect13. Here, the inherent mechanism to suppress the recoil lies in the fact that the conservation of momentum is actually satisfied by the solid crystal as a whole instead of by a single nucleus alone. In a recoil-free scattering process based on the Mössbauer mechanism, the novel quantum optical phenomena, such as the collective Lamb shift and the electromagnetically-induced-transparency (EIT)-like phenomena14,15, were displayed in an ensemble of nuclei interacting with the intense coherent photons from the synchrotron radiation light sources.
It is believed that there will emerge more exciting quantum optical effects, as photons of much better coherence and of much greater beam intensity shall be utilized, which are produced from a novel generation of light sources, such as the hard X-ray or gamma-ray free-electron laser (FEL). Stimulated by the great progress in the high energy coherent light source16,17,18,19,20,21, a novel research field, the X-ray quantum optics22 is gaining momentum to be born in the near future. At that time, when the high energy photons, with perfect coherence, interact with nuclei (especially for free atoms in the in situ x-ray measurement23,24), the recoil effect will become dominant to lead to new quantum phenomena beyond the Mössbauer effect. It is worthy to notice that the existing theoretical studies25,26 only work well for the situation that the nuclei are perfectly fixed by the solid crystal.
We set up a fully quantum model to directly manifest the main characteristics of the recoil effects in the single-photon scattering by a motional scatterer. In our one-dimensional (1D) model, the motional scatterer is modeled as a TLS confined by a harmonic potential and assume the 1D photon field has a linear dispersion relation, which is a good approximation of the usual 3D case. The Lamb-Dicke parameter (LDP)27, which is proportional to both the wave number of the resonant photon and the spatial spread of the TLS's ground state wavefunction, quantifies the coupling strength of the TLS's internal state to its motional state and thus controls the recoil strength of the TLS in the photon scattering process. In the Lamb-Dicke limit when the LDP is very small, the scattering process is recoil-free and in the reflection spectrum there is a single peak of complete reflection at the resonance point. As the LDP becomes larger, the recoil effect in the scattering process becomes more evident. A main characteristic of the recoil effect is the phonon induced multi-peaks in the reflection spectrum; moreover, the scattered photon splits into a mixed state due to its entanglement with the TLS's motional state and each component of the mixed state has a separate frequency shift.
Results
Model setup
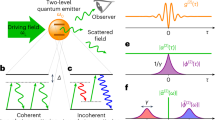
As schematically shown in Fig. 1, what we consider is a 1D system, consisting of a TLS, whose mass is M and the internal energy level spacing between the excited state |e〉 and the ground state |g〉 is Ω. The spatial confinement of the TLS is modeled by a harmonic potential of the oscillator frequency ω and therefore the motional state of the TLS is denoted by a Fock state |n〉. Let a† (a) be the creation (annihilation) operator of the vibrational quanta (phonons). Then the TLS's position (momentum) operator reads as

with  . Therefore, the Hamiltonian involving the motional TLS alone reads as
. Therefore, the Hamiltonian involving the motional TLS alone reads as

and the corresponding energy level diagram is shown in Fig. 2. While the fixed TLS has two levels, the motional TLS has two sidebands made up of many sublevels. The state of the motional TLS is denoted by |g, n〉 or |e, n〉, which means the internal state is |g〉 or |e〉 and the motional state is |n〉.
(a) Schematic of a single photon with wave number k incident on the motional two-level system (TLS) with transition frequency Ω. (b) The TLS is trapped by a harmonic potential. Here, the upper green (lower blue) harmonic oscillator represents the energy levels of the TLS in the internal excited (ground) state.
The Hamiltonian of the 1D photon field is

with ωk = υg|k|, where k is the photon wavevector and υg is the velocity of the confined photon28.
In the rotating wave approximation, the dipole coupling of the TLS to the 1D photon field is described as

Here, J is the frequency-independent coupling between the photon field and the TLS;  is the creation (annihilation) operator of the photon field, obeying the bosonic commutation relations
is the creation (annihilation) operator of the photon field, obeying the bosonic commutation relations  is the internal transition operator, i.e. σ+ = |e〉 〈g|, σ− = |g〉 〈e|; exp [±iαk(a† + a)] is known as the displacement operator, which can creat a coherent state acting on vacuum. In this model, the displacement operator causes transitions between different motional Fock states. Thus, we name it the transition operator here. The LDP, denoted as εLD, is given by
is the internal transition operator, i.e. σ+ = |e〉 〈g|, σ− = |g〉 〈e|; exp [±iαk(a† + a)] is known as the displacement operator, which can creat a coherent state acting on vacuum. In this model, the displacement operator causes transitions between different motional Fock states. Thus, we name it the transition operator here. The LDP, denoted as εLD, is given by

where kc is the resonant wave number, i.e., kc = Ω/υg.
Single-photon scattering equation
A photon propagating in 1D will inevitably encounter the TLS. The virtual absorption and emission of the photon by the TLS dramatically affect the coherent transport of the incident photon, which could be described as a single-photon scattering process by the TLS.
A single photon, incident from the left side and with wave number k, propagates in 1D, until it is scattered by the TLS, which is initially in the lowest energy state. The input state for scattering is  , where |vac〉 represents the vacuum of the photon field and |g, 0〉 is the lowest energy state of the TLS. In the scattering process, the TLS may virtually absorb and spontaneously emit a photon, which transfers the single-excitation from the photon field to the internal state of the TLS or vice versa. Additionally, the vibrational motion of the TLS is disturbed and thus the number of phononic excitations may be changed.
, where |vac〉 represents the vacuum of the photon field and |g, 0〉 is the lowest energy state of the TLS. In the scattering process, the TLS may virtually absorb and spontaneously emit a photon, which transfers the single-excitation from the photon field to the internal state of the TLS or vice versa. Additionally, the vibrational motion of the TLS is disturbed and thus the number of phononic excitations may be changed.
In the single-excitation subspace spanned by the basis |g, m〉 and |e, n〉 (m and n are the phonon numbers), the scattering state can be written as

The wavefunctions ug(p, n) and ue(n) obey the Lippmann Schwinger equation

where  and Ek,0 = ωk + ω/2. It follows from equations(5)(6) that
and Ek,0 = ωk + ω/2. It follows from equations(5)(6) that


where ωp,n = ωp + (n + 1/2)ω, ωe,m = Ω + (m + 1/2)ω and

Note that for motional TLS, the effective coupling to the photon field is indeed the coupling constant J times the vibrational transition amplitude

where  is the generalized Laguerre polynomial29. Note that due to the decay factor exp(−α2p2/2) in Eq.(10), the effective coupling strength decays as the photon momentum increases. It follows from Eq.(8) that different phononic states of the TLS are coupled via the photon field. The matrix F(m, n) gives the self-energy of the TLS due to resonant coupling with the photon field.
is the generalized Laguerre polynomial29. Note that due to the decay factor exp(−α2p2/2) in Eq.(10), the effective coupling strength decays as the photon momentum increases. It follows from Eq.(8) that different phononic states of the TLS are coupled via the photon field. The matrix F(m, n) gives the self-energy of the TLS due to resonant coupling with the photon field.
Now we calculate the single-photon scattering probability, according to the scattering state obtained. To this end, we first reform the scattering state in the coordinate representation as

where


From equation(7) and equation(13), we can obtain the photon wavefunction ug(x, n). Actually, to study the scattering problem, we only need to know the wavefunction in the limit |x| → ∞,

where kn ≡ k − nω/υg and tn (rn) is the transmission (reflection) amplitude30,


Note that the photon is scattered into a mixed state, due to the contribution of the phononic states with n ≠ 0. Each pure state component corresponds to a phononic Fock state. Thus, we can label the pure state components by the corresponding phonon numbers. Namely, the photon wavefunction of the nth pure state component with n phonons is denoted by ϕn(x). It follows from Eq.(11) that ϕn(x) = ug(x, n). For the nth pure state component, the reflectance is |rn(k)|2 and the transmittance is |tn(k)|2. The total reflectance (transmittance) Rk (Tk) is a statistical sum of each pure state component,


According to equations(8)(15)(16)(17)(18), we numerically obtain the total reflectance (transmittance), from which the probability current conservation, i.e. Tk + Rk = 1, is confirmed.
The Lamb-Dicke limit
The recoil effects in the single-photon scattering arise from the vibrational transition operator exp [±iαk(a† + a)] and the recoil strength depends on the LDP. In the Lamb-Dicke limit, αkc → 0, the vibrational transition operator can be expanded to the lowest order, i.e.  . Consequently, the recoil vanishes and the model reduces to the ideal case1. The reflectance (transmittance) is given by
. Consequently, the recoil vanishes and the model reduces to the ideal case1. The reflectance (transmittance) is given by


with Γ = 2πJ2/υg. The probability current conservation Tk + Rk = 1 holds. Therefore, we are only concerned with the reflectance Rk. We plot the reflection spectrum Rk in Fig. 3. It is observed that complete reflection occurs at the resonant point ωk/Ω = 1 and Γ/Ω is the width of the reflection peak. When the coupling strength J is very weak, a sharp reflection peak is obtained. In the scattering process the motional state of the TLS remains in the Fock state |0〉 and thus the scattered photon is in a pure state.
The recoil effects
As stated above, the recoil strength is fixed by LDP. In the limit αkc → 0, the recoil vanishes; as αkc increases, the recoil becomes more important. In the Lamb-Dicke regime  , let us expand the vibrational transition operator in α as
, let us expand the vibrational transition operator in α as

If we keep only the zeroth order,  , the TLS may absorb the photon by internal transition, but its vibrational motion is not affected. Therefore, there is only one resonance at ωk = Ω. If we keep up to the first order,
, the TLS may absorb the photon by internal transition, but its vibrational motion is not affected. Therefore, there is only one resonance at ωk = Ω. If we keep up to the first order,  , the TLS may absorb the incident photon and meanwhile, its vibrational motion gains a phonon or remains in the lowest sublevel. As a result, the outgoing photon is in a mixed state, of which a component has the resonance energy ωk = Ω, leaving the TLS in the lowest sublevel and the other component has the resonance energy ωk = Ω + ω, leaving the TLS in the second lowest sublevel. As α increases, higher-order phonon processes take effect. In consequence the scattered photon splits into a mixed state, of which each pure state component is entangled with a phononic state of the recoiled TLS and has a separate resonance energy.
, the TLS may absorb the incident photon and meanwhile, its vibrational motion gains a phonon or remains in the lowest sublevel. As a result, the outgoing photon is in a mixed state, of which a component has the resonance energy ωk = Ω, leaving the TLS in the lowest sublevel and the other component has the resonance energy ωk = Ω + ω, leaving the TLS in the second lowest sublevel. As α increases, higher-order phonon processes take effect. In consequence the scattered photon splits into a mixed state, of which each pure state component is entangled with a phononic state of the recoiled TLS and has a separate resonance energy.
To manifest the recoil effects, in Fig. 4 we compare the reflection spectra as LDP varies. When εLD is very small, the reflection spectrum coincides with the Lamb-Dicke limit. As εLD increases, the reflection peak at ωk/Ω = 1 is lowered and more peaks emerge in the vicinity of the points ωk = Ω + nω, with  .
.
The emergent multi-peaks in the reflection spectrum can also be well understood in an intuitive way. As shown in Fig. 2, the phononic excitations in the vibrational motion of the TLS bring side-bands to the energy level structure of the motional TLS. As a result, instead of the single transition between two levels for fixed TLS, there are different transitions between the side-bands and thus multi-peaks arise. For TLS initially in the lowest sublevel, the transitions are shown by the dashed lines in Fig. 2 and the corresponding resonance energies are Ω, Ω + ω, Ω + 2ω. If the TLS is initially in a high sublevel, the transitions are shown by the dotted lines in Fig. 2, with the resonance energy Ω − ω, Ω − 2ω, Ω − 3ω.
The locations of the resonance peaks are illustrated in Fig. 5, which compares the reflection spectra as ω/Ω varies. Note that the locations of the reflection peaks are shifted from the transition frequencies Ω + nω (with the integer n) of the transition channels depicted in Fig. 2. The transition channels depicted in Fig. 2 are coupled with each other, due to their interaction with the common photon field. Thus, the locations of the reflection peaks, which are actually defined by the transition frequencies of the diagonalized channels, are shifted from the transition frequencies Ω + nω by an amount increasing with the coupling strength. This phenomenon can also be interpreted by the Lamb shift of the TLS's energy level.
Besides multi-peaks in the reflection spectrum, which is a typical effect due to the recoil of the TLS, the coupling strength is also modified by the vibrational motion of the TLS. In the Lamb-Dicke limit, the coupling strength is J, whereas for motional TLS, the effective coupling is rescaled by the vibrational transition amplitude, which varies with LDP, as written in equation(10). In the limit α → ∞, the rescaling factor approaches zero, which means the coupling between the photon and the TLS is negligible. As demonstrated in Fig. 4, the reflection diminishes with εLD increasing and in the limit εLD → ∞, the reflection vanishes.
The coupling strength between the photon field and the TLS is indicated by the dimensionless parameter Γ/Ω. As shown in Fig. 6, when Γ/Ω increases, the reflection increases and also, the width of the peaks increases. The peaks merge into a single peak, when the width of the peaks is large enough to fill out the spacing between them. In addition, the location shift of the reflection peaks also increases with Γ/Ω increasing.
Apart from the reflection spectrum, the recoil also shifts the frequency of the outgoing photon. In the Lamb-Dicke limit, the contribution of the phononic states with n ≠ 0 vanishes, so that the scattering state is simplified as

Note that the scattered photon is in a pure state described by the wavefunction ug(x), which in the limit |x| → ∞ takes the form

It is observed from Eq.(23) that the frequency of the outgoing photon is still ωk. In contrast, considering recoil effects, the scattered photon is in a mixed state, of which the nth pure state component is described by the wavefunction ϕn(x) = ug(x, n), which in the limit |x| → ∞ takes the form

with kn ≡ k − nω/υg. It is observed that the frequency of the outgoing photon is ωk − nω, with nω lost to excite n phonons in the vibrational motion of the TLS.
Discussion
We have studied the 1D single-photon scattering with a motional TLS confined by a harmonic potential. In the Lamb-Dicke limit when the trap frequency is very high or the mass of the TLS is very large, we recover the results of previous studies1,2, which assume the TLS is perfectly fixed and get a reflection spectrum with only a single peak of complete reflection at the resonance point ωk = Ω. As the trap becomes looser or the mass of the TLS becomes smaller, the recoil of the motional TLS brings about new features to the single-photon transport. The original single peak of complete reflection is lowered and its location has a small shift from the resonance point ωk = Ω. Besides, multi-peaks induced by phonon excitations are observed in the neighborhood of the points  in the reflection spectrum. Besides, the properties of the scattered photon are also changed. To be specific, it splits into a mixed state due to its entanglement with the TLS's motional state and each component of the mixed state has a separate red shift with respect to the incident photon, due to energy exchange with phonon excitations.
in the reflection spectrum. Besides, the properties of the scattered photon are also changed. To be specific, it splits into a mixed state due to its entanglement with the TLS's motional state and each component of the mixed state has a separate red shift with respect to the incident photon, due to energy exchange with phonon excitations.
In the quantum devices such as a quantum switch or a single-photon transistor, the recoil should be avoided. However, the TLS cannot be absolutely fixed in practice, namely, the Lamb-Dicke parameter cannot equal zero. Note that the real incident light is always a wave packet. Since it is a linear mapping from the incoming wave to the outgoing wave, the scattering property of a wave packet can be directly obtained based on the single photon reflection spectrum. Although the recoil cannot be totally avoided, its effects can be suppressed under certain conditions. If the characteristic frequency of the harmonic potential is much larger than the energy width of the wave packet, the small multi-peaks will not take effect. Otherwise, the wavepacket of light shall be broadened and deformed after scattering.
On the other hand, the recoil may be useful, in preparing a phonon Fock state in the harmonic potential. Note that the characteristic frequency of the harmonic potential can be measured by exploring the reflection spectrum using monochromatic light. A phonon Fock state in the harmonic potential can be prepared by scattering of light with a particular frequency.
The atomic recoil in 3D light scattering also brings fasinating effects, which are out of the scope of this paper and here we cite some references31,32,33,34,35,36 for interested readers.
Methods
Numerical calculations of the reflectance
Using the formula  with
with  denoting the principal value, F(m, n) can be decomposed as the principal-value integral and the imaginary part, both of which can then be numerically calculated.
denoting the principal value, F(m, n) can be decomposed as the principal-value integral and the imaginary part, both of which can then be numerically calculated.


where we have introduced the notations


Note that the principal-value integral is convergent, because the effective coupling strength decays with the photon momentum increasing. The real part ReF(m, n) contributes to the Lamb shift of the TLS in different motional states, while the imaginary part of F(m, n) determines the decay rate of the excited TLS. Note that in the imaginary part, the phononic space is truncated by  (the total energy of phonons is no more than the incident photon), whereas in the principal-value integral, there is not a natural truncation of the phononic space. Let us assume the dimension of the phononic space is υgk/ω + Nmore. In the numerical calculation of the principal-value integral, one can start with the truncation Nmore = 0 and then gradually extend the truncation until the reflectance is convergent upon increasing Nmore. In this paper, the data in the figures is obtained by setting Nmore = 10. By increasing Nmore, the numerical value of the Lamb shift will become more precise, but no qualitative changes will happen.
(the total energy of phonons is no more than the incident photon), whereas in the principal-value integral, there is not a natural truncation of the phononic space. Let us assume the dimension of the phononic space is υgk/ω + Nmore. In the numerical calculation of the principal-value integral, one can start with the truncation Nmore = 0 and then gradually extend the truncation until the reflectance is convergent upon increasing Nmore. In this paper, the data in the figures is obtained by setting Nmore = 10. By increasing Nmore, the numerical value of the Lamb shift will become more precise, but no qualitative changes will happen.
Derivation of equations (19) and (20)
The result in the Lamb-Dicke limit can be obtained by setting α = 0. In the limit α → 0, equations(8)(9) become


It follows from Eq.(28) that the TLS remains in the lowest motional state (no phononic excitation) and thus the self-energy matrix is diagonalized. In the Lamb-Dicke limit the principal-value integral has an ultraviolet divergence, which is caused by the high momentum photons coupled to the TLS with equal strength. In order to obtain the Lamb shift, a renormalization procedure should be performed to eliminate the divergence. Since the Lamb shift is in general a very small correction to the energy level of the TLS, we have it neglected in Eq.(27) (see Refs. 1, 28). Actually, Eq.(28) is exact when Ω is identified with the renormalized level spacing.
With Eq.(28), the scattering wavefunction ug(x, n) in Eq.(14) is simplified as

which demonstrates that the motional state of the TLS remains in the Fock state|0〉 and thus the scattered photon is in a pure state. From equation(29), we read the reflection (transmission) amplitude as


and then the reflectance (transmittance) is obtained, Tk = |t(k)|2, Rk = |r(k)|2.
References
Shen, J. T. & Fan, S. Coherent photon transport from spontaneous emission in one-dimensional waveguides. Opt. Lett. 30, 2001–2003 (2005).
Zhou, L., Gong, Z. R., Liu, Y. X., Sun, C. P. & Nori, F. Controllable scattering of a single photon inside a one-dimensional resonator waveguide. Phys. Rev. Lett. 101, 100501 (2008).
Chang, D. E., Chang, D. E., Sørensen, A. S., Demler, E. A. & Lukin, M. D. A single-photon transistor using nanoscale surface plasmons. Nature Phys. 3, 807–812 (2007).
Zhou, L. et al. Quantum supercavity with atomic mirrors. Phys. Rev. A 78, 063827 (2008).
Zhou, L., Yang, S., Liu, Y. X., Sun, C. P. & Nori, F. Quantum Zeno switch for single-photon coherent transport. Phys. Rev. A 80, 062109 (2009).
Shi, T. & Sun, C. P. Lehmann-Symanzik-Zimmermann reduction approach to multiphoton scattering in coupled-resonator arrays. Phys. Rev. B 79, 205111 (2009).
Shi, T., Fan, S. & Sun, C. P. Two-photon transport in a waveguide coupled to a cavity in a two-level system. Phys. Rev. A 84, 063803 (2011).
Chang, Y., Gong, Z. R. & Sun, C. P. Multiatomic mirror for perfect reflection of single photons in a wide band of frequency. Phys. Rev. A 83, 013825 (2011).
Yan, C. H., Wei, L. F., Jia, W. Z. & Shen, J. T. Controlling resonant photonic transport along optical waveguides by two-level atoms. Phys. Rev. A 84, 045801 (2011).
Wang, Z. H., Li, Y., Zhou, D. L., Sun, C. P. & Zhang, P. Single-photon scattering on a strongly dressed atom. Phys. Rev. A 86, 023824 (2012).
Huang, J. F., Liao, J. Q. & Sun, C. P. Photon blockade induced by atoms with Rydberg coupling. Phys. Rev. A 87, 023822 (2013).
Craig, P. P., Dash, J. G., McGuire, A. D., Nagle, D. & Reiswig, R. R. Nuclear Resonance Absorption of Gamma Rays in Ir191. Phys. Rev. Lett. 3, 221–223 (1959).
Mössbauer, R. L. Kernresonanzfluoreszenz von Gammastrahlung in Ir191. Z. Physik 151, 124–143 (1958).
Röhlsberger, R., Schlage, K., Sahoo, B., Couet, S. & Rüffer, R. Collective Lamb shift in single-photon superradiance. Science 328, 1248–1251 (2010).
Röhlsberger, R., Wille, H. C., Schlage, K. & Sahoo, B. Electromagnetically induced transparency with resonant nuclei in a cavity. Nature 482, 199–203 (2012).
Ackermann, W. et al. Operation of a free-electron laser from the extreme ultraviolet to the water window. Nature Photonics 1, 336–342 (2007).
Emma, P. et al. First lasing and operation of an ångstrom-wavelength free-electron laser. Nature Photonics 4, 641–647 (2010).
Pile, D. X-rays: first light from SACLA. Nature Photonics 5, 456–457 (2011).
Rohringer, N. et al. Atomic inner-shell X-ray laser at 1.46 nanometres pumped by an X-ray free-electron laser. Nature 481, 488–491 (2012).
Di Piazza, A., Müller, C., Hatsagortsyan, K. Z. & Keitel, C. H. Extremely high-intensity laser interactions with fundamental quantum systems. Rev. Mod. Phys. 84, 1177 (2012).
Kohler, M. C., Pfeifer, T., Hatsagortsyan, K. Z. & Keitel, C. H. Frontiers of Atomic High-Harmonic Generation. Adv. AMO Phys. 61, 159–208 (2012).
Adams, B. W. et al. X-ray quantum optics. J. Mod. Opt. 60, 2–21 (2013).
Couet, S., Diederich, T., Schlage, K. & Röhlsberger, R. A compact UHV deposition system for in situ study of ultrathin films via hard x-ray scattering and spectroscopy. Rev. Sci. Instrum. 79, 093908 (2008).
Slobodskyy, T. et al. A portable molecular beam epitaxy system for in situ x-ray investigations at synchrotron beamlines. Rev. Sci. Instrum. 83, 105112 (2012).
Röhlsberger, R., Klein, T., Schlage, K., Leupold, O. & Rüffer, R. Coherent x-ray scattering from ultrathin probe layers. Phys. Rev. B 69, 235412 (2004).
Xu, D. Z., Li, Y., Sun, C. P. & Zhang, P. Collective effects of multi-scatterer on coherent propagation of photon in a two dimensional network. arXiv:1212.5688. (2012).
Javanainen, J. & Stenholm, S. Laser cooling of trapped particles III: The Lamb-Dicke limit. Appl. Phys. 24, 151–162 (1981).
Shen, J. T. & Fan, S. Theory of single-photon transport in a single-mode waveguide. I. Coupling to a cavity containing a two-level atom. Phys. Rev. A 79, 023837 (2009).
Cahill, K. E. & Glauber, R. J. Ordered Expansions in Boson Amplitude Operators. Phys. Rev. 177, 1857 (1969).
Taylor, J. R. Scattering Theory: The Quantum Theory on Nonrelativistic Collisions. John Wiley & Sons, Inc (1972).
Politzer, H. D. Light incident on a Bose-condensed gas. Phys. Rev. A 43, 6444–6446 (1991).
Lewenstein, M. & You, L. Probing Bose-Einstein condensed atoms with short laser pulses. Phys. Rev. Lett. 71, 1339–1342 (1993).
Stamper-Kurn, D. M. et al. Excitation of Phonons in a Bose-Einstein Condensate by Light Scattering. Phys. Rev. Lett. 83, 2876–2879 (1999).
Piovella, N., Gatelli, M. & Bonifacio, R. Quantum effects in the collective light scattering by coherent atomic recoil in a Bose–Einstein condensate. Opt. Commun. 194, 167–173 (2001).
Campbell, G. K. et al. Photon Recoil Momentum in Dispersive Media. Phys. Rev. Lett. 94, 170403 (2005).
Slama, S., Bux, S., Krenz, G., Zimmermann, C. & Courteille, Ph. W. Superradiant Rayleigh Scattering and Collective Atomic Recoil Lasing in a Ring Cavity. Phys. Rev. Lett. 98, 053603 (2007).
Acknowledgements
Thanks to P. Zhang and J. Q. Liao for helpful discussions. This work is supported by National Natural Science Foundation of China under Grants No. 11121403, No. 10935010 and No. 11074261.
Author information
Authors and Affiliations
Contributions
Q.L. wrote the main manuscript text and did the calculations, D.Z.X. and C.Y.C. helped with calculations and discussions, C.P.S. designed and supervised the project and revised the manuscript. All authors reviewed the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Li, Q., Xu, D., Cai, C. et al. Recoil effects of a motional scatterer on single-photon scattering in one dimension. Sci Rep 3, 3144 (2013). https://doi.org/10.1038/srep03144
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep03144
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.







 .
.