Introduction

Hafnia ferroelectrics1,2—including HfO2, Hf1−xZrxO2, ZrO2 and doped variations—attract attention because of their technological promise3 and surprising properties, from their resilient polar order in nanostructures1 to their tunable piezoresponse4. Understanding their behavior is challenging, though, a major difficulty coming from the variety of intrinsic and extrinsic factors that influence the observed properties. Even if we focus on the intrinsic features of perfect crystals, as those considered in quantum computer simulations, these materials prove exceedingly intriguing.

Recent works show that, in the case of the most common ferroelectric phase of hafnia (orthorhombic with space group Pca21), some most basic questions—e.g., what should be the centrosymmetric state that can be used as a reference to compute the polarization5,6—are not resolved yet. In fact, we contend that the common theoretical treatments7,8—which assume the well-known tetragonal (P42/nmc) or cubic (\(Fm\bar{3}m\)) phases as reference structure—are not ideally suited to discuss the behavior of the woken-up ferroelectric phase of these materials. Indeed, such approaches yield involved models that hamper the discussion of the relevant low-energy landscape. Then, based on first-principles simulations, we show that there exists an alternative reference state that solves these issues while providing us with an appealing picture of the ferroelectric state and its properties.

Results

Reasons for an alternative approach to hafnia

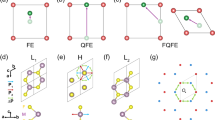
Let us first discuss the issues we see in current treatments. Figure 1a sketches the tetragonal phase most frequently considered as the centrosymmetric reference in discussions of ferroelectricity in hafnia (P42/nmc space group, “t” in the following). The figure also shows the variants of the Pca21 ferroelectric phase ("o-III” in the following) obtained from this t-reference. The distortion from t to o-III breaks the tetragonal 4-fold axis, and the resulting polarization can adopt four symmetry-equivalent orientations within the plane of the figure, (±P, 0) and (0, ±P). Accordingly, one would expect to find four different domains in hafnia samples. For example, we could have 90° ferroelectric and ferroelastic domain walls separating regions with P = (P, 0) and P = (0, P). Such 90° boundaries have indeed been observed at intermediate stages during the electric cycling frequently required to wake up hafnia samples9,10, as the material visits intermediate states with coexisting regions of in-plane (as-grown) and out-of-plane (poled) polarization. Similar 90° walls have also been observed upon ferroelectric switching in some samples11. The reported 90° walls would be nominally charged and of very high energy according to Density Functional Theory (DFT) calculations12, which suggests yet-undetermined screening mechanisms might be at play. At any rate, beyond some lingering mysteries, the observations clearly indicate that in some situations—particularly during wake-up cycling—hafnia behaves as a ferroelastic biaxial (even triaxial) material, which demands a theory based on a tetragonal (even cubic) high-symmetry reference structure.

Fig. 1: Ferroelectric domains expected in hafnia.
figure 1

a shows the tetragonal (t) phase of hafnia (center) and the four orthorhombic ferroelectric (o-III) variants it leads to. b shows the orthorhombic centrosymmetric phase (o-ref) we propose as reference (center) and the two o-III domains it leads to. Hafnium atoms are shown in blue. The active oxygens, responsible for the development of the spontaneous polarization, are shown in red; the other oxygens are shown in orange. Black arrows indicate spontaneous polarization, which goes against the displacement of the active oxygens from the reference structure. The computed polarization with respect to the t-phase for the structure marked with an asterisk in (a) is +0.54 C m−2; by contrast, the polarization with respect to the o-ref phase of the structure marked with an asterisk in (b) is −0.68 C m−2, while the one marked with a dagger presents +0.68 C m−2. (As shown in Supplementary Note 1, +0.54 C m−2 and −0.68 C m−2 differ by two polarization quanta.) Lattice constants are indicated.

Full size image

By contrast, we think there are reasons to believe that the treatment of woken-up hafnia samples could be much simpler. Experimental studies13 suggest that woken-up hafnia and zirconia samples often present a coexistence of phases, including the o-III ferroelectric state, the well-known monoclinic ground state (m-phase) and other low-energy orthorhombic polymorphs (e.g., those usually denoted o-I and o-I*14). Remarkably, microscopy images suggest that such polymorphs are separated by boundaries of essentially zero width13,15. In fact, such polytypic states appear to be a well-oriented structure where all the polymorphs share a common (anti)polar axis of sorts. (This statement will be made precise below). These conclusions are reinforced by recent first-principles investigations of ferroelectric switching in hafnia16: the most likely paths involve intermediate structures that share atomic motifs with the low-energy phases of the material (m, o-I and o-I*), all displaying a common (anti)polar axis. Hence, it seems reasonable to hypothesize a uniaxial behavior and examine to what extent it may yield a simpler—and useful—theoretical description.

An additional issue pertains to the nature of ferroelectricity. Figure 2a shows the energy of hafnia computed along a path connecting t and o-III. (See “Methods” for calculation details). Both structures are local energy minima, separated by a barrier, suggesting that a transition between them should be discontinuous (first-order). Further, if the energy landscape is analyzed in terms of symmetry-adapted modes8, one concludes that the o-III state displays an improper ferroelectric behavior, whereby the spontaneous polarization relies on the occurrence of several non-polar modes. This picture is appealing because hafnia exhibits features typical of improper ferroelectrics (e.g., large coercive fields, resilience of the polar order at the nanoscale). However, fresh experiments17 question this interpretation.

Fig. 2: Energy landscape connecting key HfO2 polymorphs.
figure 2

The black lines show the computed energy variation between the t and o-III phases (a), o-III and o-ref (b), and o-ref and m (c). The energies are computed for intermediate structures obtained by linear interpolation between the corresponding end-point polymorphs. The red line in (b) shows the energy variation of the o-ref state upon condensation of the \({\Gamma }_{2}^{-}\) distortions present in the o-III phase; the red line in (c) shows the analogous result when considering only the \({\Gamma }_{4}^{+}\) phonon distortions present in the m-phase. The blue line in (c) shows the result of condensing together the \({\Gamma }_{4}^{+}\) phonon and shear strain distortions present in the m-phase, while the green line shows the energy variation associated with the shear alone. In (b) and (c), the additional distortions leading to the black line are fully symmetric \({\Gamma }_{1}^{+}\) modes, including the normal cell strains.

Full size image

Schroeder et al.17 have recently reported a strong dielectric anomaly (ϵr ≈ 8000) upon heating Hf0.5Zr0.5O2 across what seems to be a ferroelectric phase transition. The authors note that the observed behavior is reminiscent of proper ferroelectrics like BaTiO3, which presents a first-order transition driven by a soft mode with a high permittivity maximum (ϵr ≈ 10,000) associated with it18. In line with previous experimental19,20,21 and theoretical22,23 reports of a transition between the t and o-III phases, the authors assume that the measured dielectric anomaly occurs at the temperature where the ferroelectric polymorph becomes unstable in favor of the tetragonal one. There is a difficulty with this picture, though: it is not consistent with (in fact, it goes against) what we know about proper soft-mode ferroelectricity in perovskite oxides. Indeed, DFT simulations of BaTiO3 show that the paraelectric cubic state presents a dominant polar instability24,25, which is the hallmark of proper ferroelectricity driven by a soft mode. The situation in hafnia is different: according to DFT, the t-phase presents no indication of a polar instability (see Supplementary Fig. S1) and, thus, there is no support for proper soft-mode ferroelectricity. If anything, DFT suggests that a transition between o-III and t would be similar to the ferroelectric-paraelectric transition in BiFeO326: a non-soft-mode transformation between two states that DFT describes as local energy minima27, and which experimentally has a weak dielectric anomaly (ϵr ≈ 65) associated to it28,29.

Uniaxial picture of hafnia

Let us now discuss the picture of hafnia that emerges if we consider a different centrosymmetric reference, namely, the orthorhombic Pbcm state denoted “o-ref” in Fig. 1b. This structure is similar to o-III, except that the active oxygens (red in the figure) are located within the same plane as the Hf atoms. This o-ref phase has been discussed in theoretical investigations of ferroelectric switching as a potential transition state5,6,30. Further, this polymorph has probably been observed experimentally in ZrO2 under pressure31 and as an adaptive martensite phase in ZrO2 nanoparticles32. At any rate, let us stress that, for the present purposes, it is not critical whether this polymorph actually occurs or not. Note that, for example, the cubic paraelectric phase of BiFeO3 is all but inaccessible experimentally33; yet, it is the relevant reference to explain the observed ferroelectric domains.

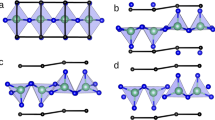
Figure 3a shows the phonon bands computed for the o-ref phase. We find a small number of unstable bands with well-defined character: they feature off-plane displacements of the active oxygens. At the Γ point of the Brillouin zone, there is a dominant instability: a polar mode with symmetry \({\Gamma }_{2}^{-}\) that captures the distortion connecting o-ref and o-III (Fig. 3b, c). Indeed, standard symmetry analysis34,35 shows that o-III can be obtained from o-ref by distortions of \({\Gamma }_{2}^{-}\) and \({\Gamma }_{1}^{+}\) symmetries, the latter being fully symmetric modes not relevant in this discussion. The black curve in Fig. 2b shows the energy variation associated with this transformation: a simple potential well with a minimum of about 177 meV per formula unit (f.u.) below o-ref. Thus, an energy expansion around o-ref naturally provides a framework to describe soft-mode-driven proper ferroelectric behavior, as that of BaTiO3. Further, the \({\Gamma }_{2}^{-}\) irreducible representation is one-dimensional; thus, we have uniaxial ferroelectricity, as sketched in Fig. 1b.

Fig. 3: Phonon bands of the o-ref phase.
figure 3

a shows the computed bands, presenting imaginary frequencies as negative values. The most important unstable modes are marked in (a). We also show the corresponding eigenmodes and the polymorphs they lead to: the \({\Gamma }_{2}^{-}\) soft mode (b) and the corresponding o-III phase (c); the \({X}_{2}^{-}\) soft mode (d) and the corresponding o-I phase (e); the \({\Gamma }_{4}^{+}\) soft mode (f) and the associated m-phase (g); and the \({X}_{4}^{+}\) soft mode (h) and the corresponding o-I* phase (i). We mark in red the active oxygens whose displacements characterize these phonons. For the polymorphs, we indicate the energy with respect to o-ref.

Full size image

Incidentally, let us note that, as discussed in Supplementary Note 1 and previous literature5,6, using o-ref instead of the t-phase as a centrosymmetric reference leads to a different—but related within the Berry-phase theory36—quantification of the polarization of the o-III phase.

If we follow the \({\Gamma }_{2}^{-}\) soft mode along the Γ − X direction of the Brillouin zone, we reach a stronger instability: the antipolar \({X}_{2}^{-}\) mode in Fig. 3d. This distortion yields another low-energy polymorph: the orthorhombic Pbca phase depicted in Fig. 3e, which is usually denoted “o-I”14 and has been experimentally observed in ZrO237. Symmetry analysis shows that o-ref and o-I are connected solely by \({X}_{2}^{-}\) and fully symmetric distortions. The o-I state is more favorable than the ferroelectric o-III phase, by about 17 meV per f.u. Further, this state can be seen as a sequence of ultra-thin ferroelectric stripe domains, where the polarization of the o-III phase is modulated along the horizontal direction in Fig. 3b. From this perspective, we can say that the domain walls of the o-III phase have a negative formation energy (of about −84 mJ m−2) and that ferroelectricity in hafnia is essentially two-dimensional (i.e., a single ultra-thin ferroelectric stripe can occur regardless of its surroundings). This and related observations (e.g., the slow motion of domain walls in hafnia) had been previously made38,39; here, by taking the o-ref phase as a starting point, we rediscover them in a straightforward manner.

Our calculations reveal additional soft modes worth discussing. Especially interesting is the second lowest-lying zone-center instability, with \({\Gamma }_{4}^{+}\) symmetry and an antipolar character (Fig. 3f). This distortion leads to the well-known monoclinic ground state of hafnia (P21/c “m-phase”, Fig. 3g), about 240 meV per f.u. below o-ref14,40. If we follow the \({\Gamma }_{4}^{+}\) instability as we move toward X, we reach a soft mode with symmetry \({X}_{4}^{+}\). Sketched in Fig. 3h, this mode involves an antiphase modulation of the antipolar distortion in Fig. 3f; its condensation yields the state shown in Fig. 3i, with space group Pbca and about 213 meV per f.u. below o-ref, denoted “o-I*”14 and experimentally observed15,41. Note that the m and o-I* phases are both connected to the o-ref state by distortions of well-defined symmetry (\({\Gamma }_{4}^{+}\) and \({X}_{4}^{+}\), respectively) solely accompanied by fully symmetric modes. Hence, notably, the most relevant low-energy polymorphs of hafnia (m, o-III, o-I and o-I*) can be obtained as simple proper instabilities of the o-ref phase. Additional low-energy structures—e.g., the “m-III” polar phase recently discussed in ref. 14—can also be obtained, by condensing other individual soft modes or combinations of them. Supplementary Fig. S2 shows that essentially the same applies to ZrO2.

Note that our proposed uniaxial approach to hafnia affects not only the o-III phase but also the mentioned low-lying polymorphs. All of them share an axis along which the active oxygens move, namely, the vertical direction that is common to all the structures of Fig. 3. For convenience, Supplementary Fig. S4 shows the simulated X-ray diffraction patterns for all these phases, and Supplementary Table S1 lists the corresponding lattice constants as obtained from our simulations.

The phonon frequencies of Fig. 3a pose an apparent paradox: given that the computed \({\Gamma }_{4}^{+}\) instability is weak compared to the others discussed above, how can the associated m-phase be the ground state? To answer this, in Fig. 2b, c we distinguish the energy contributions of different sets of modes to stabilize the o-III and m phases. The condensation of the \({\Gamma }_{2}^{-}\) distortion yields a large energy reduction with respect to o-ref (red curve in Fig. 2b); then, the fully symmetric \({\Gamma }_{1}^{+}\) modes react to the ferroelectric distortion and further reduce the energy (black curve) down to the actual o-III minimum. By contrast, the condensation of the \({\Gamma }_{4}^{+}\) optical distortion alone (red curve in Fig. 2c) yields a shallow energy well. Nevertheless, in the case of the m-phase, the shear strain causing the monoclinic deformation of the cell shares the \({\Gamma }_{4}^{+}\) symmetry. Hence, while stable by itself (green curve), this shear couples harmonically with the \({\Gamma }_{4}^{+}\) phonon yielding a much stronger instability (blue curve). In addition, the \({\Gamma }_{1}^{+}\) modes react to the monoclinic distortion, resulting in the very stable m-phase (black curve). Hence, by using the o-ref phase as the starting point of our analysis, we reveal the key role of the shear strain in determining the ground state of hafnia, reflected in the energetics of Fig. 2c and the fact that the total \({\Gamma }_{4}^{+}\) instability has a mixed strain-phonon character.

Our approach also sheds light on the possible transitions between stable hafnia polymorphs. For example, an electric field-driven transformation from o-I to o-III would constitute a textbook case of antiferroelectric behavior. Indeed, because the antipolar (\({X}_{2}^{-}\)) and polar (\({\Gamma }_{2}^{-}\)) instabilities belong to the same band (Fig. 3a), this appears to be an ideal antiferroelectric as discussed by Kittel42. Further, we suggest that field-driven transformations from o-I* to o-III, or from m to o-III, can also be viewed as Kittel-like antiferroelectric transitions since the polar and antipolar states have a common origin as distortions of the o-ref phase. The latter (m to o-III) would be a rare example of antiferroelectric effect involving no doubling of the unit cell. Along these lines, let us note that Kudoh et al.31 studied ZrO2 under pressure and found what seems to be an order-disorder transition from m to o-ref itself, with oxygens hopping back and forth across their high-symmetry positions in the Pbcm structure.

Our results also suggest that o-I* is structurally connected to the monoclinic ground state. In essence, this connection was already mentioned by Ohtaka et al.41; our theory confirms it and reveals its deeper origin. Indeed, viewed as a distortion of o-ref, the m-phase can present the two variants shown in Fig. 4a, with positive and negative shear, respectively. Then, as emphasized in Fig. 4b, the o-I* unit cell can be seen as composed of two matching domains corresponding to such m-variants. This is most natural: the underlying \({\Gamma }_{4}^{+}\) and \({X}_{4}^{+}\) instabilities belong to the same band, which suggests that the associated distortions correspond to different modulations of the same local motif. Such a common motif is the particular antipolar displacement of the active oxygens in Fig. 3f, which is accompanied by a relative vertical shift of the neighboring Hf planes. When this pattern repeats homogeneously (\({\Gamma }_{4}^{+}\)) it yields a net shear; when antimodulated (\({X}_{4}^{+}\)) the opposing local strains cancel out. These observations further suggest that a transition from o-I* to m, driven by an appropriate shear stress, would be an example of antiferroelastic behavior. Interestingly, antiferroelastics were introduced theoretically decades ago43, but we are not aware of any demonstration. (The term antiferroelastic has been used to denote phases that present correlated antiferrodistortive and Jahn-Teller distortions44; however, as far as we can see, such phases do not involve the antiphase strain modulations discussed by Aizu43 and shown here.) In the case of hafnia, an experimental realization would require stabilizing the o-I* state over the m-phase; given their proximity in energy (the gap is about 27 meV per f.u.) this is conceivable, e.g., by growing samples on appropriate substrates.

Fig. 4: Antiferroelastic behavior.
figure 4

a shows the two symmetry-equivalent m-phase variants that can be obtained as a \({\Gamma }_{4}^{+}\) distortion of the o-ref phase. In (b), we emphasize that the unit cell of the o-I* phase can be obtained by matching the two m-variants in (a). Hence, o-I* can be seen as composed of ultra-thin ferroelastic stripe domains (marked with dotted lines), with a domain wall energy of 126 mJ m−2.

Full size image

Discussion

We now make some remarks that put our work into perspective. Let us start by noting that Zhou et al.45 have recently used DFT to predict that, under suitable elastic constraints, the t-phase evolves into an antipolar state with Pbcn symmetry, which in turn can eventually develop a ferroelectric soft mode leading to o-III. Raeliarijaona and Cohen46 have provided an additional DFT-based discussion on how the centrosymmetric Pbcn state can yield proper ferroelectric order. We think these theories may indeed prove relevant to explain the experimentally observed dielectric anomaly and soft-mode-like behavior17. Interestingly, both these works imply an uniaxial picture of hafnia, which is justified as a result of epitaxial strain by Zhou et al.45.

On the topic of the temperature-driven transition, it is worth noting that ref. 32 showed experimental evidence—for zirconia nanoparticles—of a martensitic transformation from t to o-I through an intermediate o-ref state. Given the structural similarities between the o-I and o-III states (see Fig. 3c, e), these results suggest that a transition between o-III and t may present an intermediate orthorhombic centrosymmetric state like o-ref. If so, this could explain the soft-mode-like dielectric anomaly observed experimentally upon heating the o-III state17.

Let us briefly mention that machine-learned potentials—derived from DFT simulations—have been used to study the temperature-driven ferroelectric-to-paraelectric phase transition in both hafnia22 and zirconia23. Both works report an o-III to t transformation, involving a dielectric anomaly in the case of zirconia (ϵr ≈ 330 at 900 K)23. While valuable, we are not convinced these simulations explain the experimentally observed transformation17. On the one hand, while it reflects some lattice softening, the observed dielectric maximum is quite modest compared to the experimental one observed in hafnia (ϵr ≈ 8,000). On the other hand, the results of these studies probably depend on the training sets used to construct the machine-learned potentials, and we wonder whether the orthorhombic states discussed here or in refs. 45,46 were considered. Hence, we think this remains an open question.

Let us now consider ferroelectric switching or field-driven transitions between the low-lying polymorphs. As already mentioned, the latest experimental13 and theoretical16 results suggest that the most favorable switching paths involve hopping of the active oxygens across their high-symmetry positions in the o-ref state, giving rise to local configurations that resemble the structural motifs of the m, o-I and o-I* polymorphs. Further, these low-energy paths do not seem to involve t- or Pbcn-like configurations. Interestingly, the situation is reminiscent of the order-disorder hopping of active oxygens, around their equilibrium positions in the o-ref phase, as deduced from experiments of ZrO2 under pressure31. Such a dynamical disorder can be viewed as (local) stochastic transitions between the m, o-I, o-I* and o-III states, yielding the o-ref structure in average. Hence, in order to investigate ferroelectric switching and field-driven transitions in woken-up hafnia and zirconia, it seems most suitable to construct a theory that takes the o-ref state as starting point, so that all relevant intermediate states can be described as simple distortions of the reference structure.

We thus have the following remarkable situation. For hafnia and zirconia, we may need to work with a tetragonal or cubic reference to study the stabilization of the o-III ferroelectric state, including wake-up cycling. This implies a biaxial or triaxial material, respectively. By contrast, it may be sufficient, and physically more transparent, to build uniaxial theories based on the Pbcn or o-ref structures in order to discuss the proper ferroelectric phase transition and soft-mode-like dielectric anomaly observed experimentally. Finally, to investigate ferroelectric switching—or field-driven transformations among low-lying polymorphs—the o-ref state may offer the simplest and physically most relevant starting point. However, in our opinion, the possibility that the t-phase offers an active (competing) switching path cannot be ruled out based on the available information5,6,16, and this remains an open question.

The above disquisition may seem puzzling, particularly if one has in mind the simplicity of the best-studied ferroelectrics family, i.e., perovskite oxides like BaTiO3 or PbTiO3. There, the ideal (cubic) perovskite structure is generally taken as the high-symmetry centrosymmetric reference, for all materials and purposes. However, even among perovskites, there are subtle cases that can inform our present discussion. For example, the ferroelectric transition of BiFeO3 involves a complex paraelectric phase featuring large distortions of the ideal cubic structure (large tilts of the O6 octahedra, Pbnm space group). This non-polar state bears no group-subgroup symmetry relation with the ferroelectric phase (R3c space group); in fact, it would be hopeless to (try to) use the Pbnm state as the starting point of a theory aiming to explain the properties (domain variants, switching) of the ferroelectric phase. Hence, BiFeO3 is an example where the theory needed to explain the ferroelectric phase transition (which must account for the Pbnm phase) is different from the theory needed to model the properties of the ferroelectric state (which requires a cubic reference).

It is also worth noting the case of LiNbO347, which features a rhombohedral (R3c) ferroelectric phase that is very similar to that of BiFeO3. By analogy with BiFeO3, one would postulate a cubic reference and treat this compound as a triaxial ferroelectric. However, experiments show that LiNbO3 behaves as a uniaxial material and that a centrosymmetric rhombohedral (\(R\bar{3}c\)) phase is the paraelectric state48. Hence, a simple model taking the \(R\bar{3}c\) phase as reference—and yielding only two polarization variants—gives a description of LiNbO3 that is both simple and sufficient. LiNbO3 thus provides us with an example where phenomenological arguments—not unlike the ones made in this work—lead us to a theory that is simpler and physically sounder than the one that might have been chosen by default. See Supplementary Note 2 for further considerations on the choice of reference states in BiFeO3 and LiNbO3.

In summary, in this work, we introduce a theoretical framework ideally suited to model the functional properties of the most common ferroelectric phase of hafnia and zirconia, including switching, field-driven transitions between low-energy polymorphs, and electromechanical responses. We rely on the assumption of a uniaxial ferroic order which, according to recent experiments, seems to be relevant to many woken-up samples. We also discuss how other phenomena may require different treatments, potentially involving alternative reference phases (e.g., to address the temperature-driven ferroelectric transition) and abandoning the uniaxial hypothesis (e.g., to tackle ferroelastic effects during the wake-up process).

Within this restricted—but crucial—realm of application, our work provides a simple yet thorough picture of the relevant energy landscape of hafnia and zirconia, naturally connecting all low-energy polymorphs. In particular, the proposed reference phase appears as an ideal starting point for the development of physically transparent perturbative theories, from phenomenological Ginzburg-Landau models to coarse-grained effective Hamiltonians49 or atomistic second-principles potentials50. Further, having such a soft-mode-style model of hafnia invites (enables) us to borrow ideas from the literature on perovskite oxides, for example, to optimize the negative capacitance effect51,52. We thus expect our findings will become an important ingredient of future work on these materials, from theoretical and computational studies to the conception of new experiments and optimization strategies.

Methods

Our simulations are carried out using first-principles density functional theory (DFT) as implemented in the Vienna Ab-initio Simulation Package (VASP)53,54. We employ the Perdew-Burke-Ernzerhof formulation for solids (PBEsol)55 of the generalized gradient approximation for the exchange-correlation functional. The atomic cores are treated within the projector-augmented wave approach56, considering the following states explicitly: 5s, 5p, 6s, 5d for Hf; 4s, 4p, 5s, 4d for Zr; and 2s, 2p for O. We use a plane-wave energy cutoff of 600 eV. A 6 × 6 × 6 Monkhorst-Pack57 k-point sampling of the Brillouin zone is employed for the o-ref, m, t and o-III phases, and a 3 × 6 × 6 k-point grid is employed for the o-I and o-I phases, which are (approximately) twice as long along the first lattice vector. The structures are fully relaxed until the residual forces fall below 0.001 eVÅ−1 and residual stresses fall below 0.01 GPa. These calculation conditions yield well-converged results.

The paths shown in Fig. 2 are obtained by interpolating the lattice vectors and fractional atomic coordinates between the initial and final structures with 10 intermediate points. No structural optimization is performed for the intermediate states. Thus, for example, the green points in the figure are obtained by computing the energy of the o-ref structure distorted by a shear strain as the one of the m-phase, from zero shear (pristine o-ref) to its value in the m polymorph. The blue points give the energy of an o-ref structure distorted by condensing simultaneously the shear strain and the \({\Gamma }_{4}^{+}\) phonon distortion that appear in the m-phase, from zero (pristine o-ref) to their values in the m polymorph.

The polarization is computed using the modern theory of polarization36. Phonon bands are obtained using the direct supercell approach implemented in the PHONOPY package58. A 2 × 2 × 2 supercell is employed both for the o-ref phase of HfO2 and ZrO2 and for the t-phase of HfO2, which we find to give well-converged results. The non-analytical contribution to the phonons is considered in the calculations.

We use standard web-based crystallographic tools34,35 for symmetry analysis. The visualization package VESTA59 is used for the structure representations and to simulate X-ray diffraction patterns.