High-entropy grain boundaries

Abstract

As high-entropy alloys receive an increasing amount of attention, an interesting scientific question arises: can grain boundaries be “high entropy”? In 2016, we proposed “high-entropy grain boundaries” as the grain boundary counterparts to high-entropy materials. Here, we discuss the underlying interfacial thermodynamics to elaborate relevant concepts. We emphasize that “high-entropy grain boundaries” are neither equivalent to grain boundaries in high-entropy materials nor simply “compositionally complex grain boundaries”, but they should possess specific thermodynamic characters. Using a simplified segregation model, we illustrate that both grain boundary and bulk high-entropy effects can reduce grain boundary energy with increasing temperature for saturated multicomponent alloys, where the effective grain boundary entropy can be positive and increase with the number of components. We show that high-entropy grain boundaries can stabilize nanocrystalline alloys at high temperatures via thermodynamic and kinetic effects. Grain boundary structural disordering and transitions may offer further opportunities to attain higher effective grain boundary entropies.

Introduction

High-entropy alloys and ceramics (HEAs and HECs), which are subgroups of broader classes of compositionally complex (or complex concentrated) alloys and ceramics (CCAs and CCCs), have attracted substantial research interests recently^{1,2,3,4,5,6,7}. Here, we post an interesting scientific question: can an interface, particularly a grain boundary (GB), be “high entropy”? In 2016, we first proposed the concept and terminology of high-entropy grain boundaries (HEGBs) with a single numerical example in a Current Opinion article as a future perspective⁸. We subsequently showed that HEGBs can be utilized to stabilize nanocrystalline alloys (nanoalloys) at high temperatures⁹. While that original work⁹, particularly the idea of stabilizing nanoalloys with high-entropy effects, has caught substantial interests^{10,11,12,13,14,15,16,17,18,19,20}, a rigorous thermodynamic theory of HEGBs has not been presented. This article elaborates the relevant concepts and present a complete thermodynamic framework for the first time, and subsequently discusses the future perspective.

In a multicomponent system, a GB can certainly be compositionally complex. In fact, even if the bulk phase a conventional multicomponent alloy that is a dilute solid solution of multiple solute components, the GB can be a concentrated multi-principal component solution (Fig. 1c), thereby potentially being high entropy even if the bulk alloy is not. Here, we need to first discuss what is GB entropy and thermodynamic characters of HEGBs based on rigorous interfacial thermodynamics.

Fig. 1: Grain boundary (GB) disorder, adsorption, and entropy.

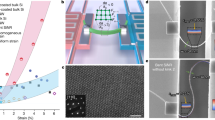
a Normalized GB energy (${\gamma }_{{GB}}/{\gamma }_{{GB}}^{(0)}$) and dγ_GB/dT vs. normalized temperature ($T/{T}_{M}$) for a Ni $\Sigma$ 79 GB (replotted after Foiles²¹ with permission ©Elsevier 2010) and a hypothetic case with a first-order GB premelting transition. b GB energy (${\gamma }_{{GB}}$) and GB adsorption ($\Gamma$) vs. bulk Bi percentage (${X}_{{{{{{\rm{Bi}}}}}}}^{{{{{{\rm{bulk}}}}}}}$) for a Bi-doped Ni general GB (replotted after Zhou et al.²³ with permission ©Elsevier 2017), where the inset is a scanning transmission electron microscopy image of Bi bilayer adsorption (reprinted after Luo et al.²⁹ with permission ©AAAS 2011). c Schematic illustration of different GB structures with increasing structural and/or chemical disorder and entropy. Insets are high-resolution transmission electron microscopy images showing coupled GB premelting and segregation in Ni-doped W (reprinted after Luo et al.³⁰ with permission ©AIP 2005).

GB entropy and interfacial thermodynamics

There are two general ways to define GB entropy. In the classical Gibbs adsorption theory, we can define the GB excess of entropy (${s}^{{{{{{\rm{xs}}}}}}}$), which has a well-defined value (independent of the Gibbs dividing plane) for a GB. For a bulk phase of a closed system, entropy (S) measures how the Gibbs free energy (G) decreases with temperature (T) at a constant pressure (P): $S=-{(\partial G/\partial T)}_{P}$. Analogously, we look for a HEGB to have a positive and large “effective GB entropy”: ${s}_{{{{{{\rm{GB}}}}}}}^{{{{{{\rm{eff}}}}}}.}\equiv -{(\partial {\gamma }_{{{{{{\rm{GB}}}}}}}/\partial T)}_{P}$, where GB energy (${\gamma }_{GB}$) decreases with increasing temperature. This also represents a beneficial feature to stabilize nanoalloys at high temperatures. However, a multicomponent GB is more complex (than a bulk phase) because it is not a closed system. Different scenarios will be discussed subsequently.

In an N-component system, interfacial energy (γ) is the interfacial excess of grand potential:

$$\gamma ={u}^{{{{{{\rm{xs}}}}}}}-T{s}^{{{{{{\rm{xs}}}}}}}-\mathop{\sum }\limits_{i=1}^{N}{\mu }_{i}{\Gamma }_{i},$$

(1)

where ${u}^{{{{{{\rm{xs}}}}}}}$, ${s}^{{{{{{\rm{xs}}}}}}}$, and ${\Gamma }_{i}$ are the interfacial excess of internal energy, entropy, and (adsorption of) the i-th component (i = 1, 2, …, N), respectively, based on the Gibbs definition. For a phase boundary, we can select the Gibbs dividing plane so that ${\Gamma }_{1}$ = 0. However, this convention cannot be adopted for a GB, where two abutting grains are the same phase, so that the GB excess quantities are independent of the position of the Gibbs dividing plane. The generalized Gibbs adsorption equation states:

$$d{\gamma }_{{{{{{\rm{GB}}}}}}}=-{s}^{{{{{{\rm{xs}}}}}}}dT+\overline{V}dP-\mathop{\sum }\limits_{i=1}^{N}{\Gamma }_{i}d{\mu }_{i}.$$

(2)

For a specific GB in a unary system, its GB energy varies with temperature at a constant pressure:

$${\Bigg(\frac{\partial {\gamma }_{{{{{{\rm{GB}}}}}}}}{\partial T}\Bigg)}_{P}=-{s}^{{{{{{\rm{xs}}}}}}}-\Gamma {\Bigg(\frac{d\mu }{dT}\Bigg)}_{P}=-({s}^{{{{{{\rm{xs}}}}}}}-\Gamma \bar{S}),$$

(3)

where $\bar{S}$ is molar entropy. Since $\Delta {v}_{{{{{{\rm{GB}}}}}}{{{{{\rm{free}}}}}}}$= $-\Gamma \overline{V}$= ${(\partial {\gamma }_{{{{{{\rm{GB}}}}}}}/\partial P)}_{T}$ is the GB “free volume” per unit area (in a unit of length), we may define the effective GB entropy for a unary GB as:

$${s}_{{{{{{\rm{GB}}}}}}}^{{{{{{\rm{eff}}}}}}.}\equiv -{\Bigg(\frac{\partial {\gamma }_{GB}}{\partial T}\Bigg)}_{P}={s}^{{{{{{\rm{xs}}}}}}}+(\bar{S}/\overline{V})\cdot \Delta {v}_{{{{{{\rm{GB}}}}}}{{{{{\rm{free}}}}}}}={s}^{{{{{{\rm{xs}}}}}}}+{S}_{V}\cdot \Delta {v}_{{{{{{\rm{GB}}}}}}{{{{{\rm{free}}}}}}},$$

(4)

where S_V (=$\bar{S}/\overline{V}$) is the volumetric entropy of the bulk phase. It is interesting to note that ${s}_{{{{{{\rm{GB}}}}}}}^{{{{{{\rm{eff.}}}}}}}\equiv -(\partial {\gamma }_{{{{{{\rm{GB}}}}}}}/\partial T)_{P} \, \ne \, {s}^{{{{{{\rm{xs}}}}}}}$ even for a simple unary GB (because $\Gamma \, \ne \, 0$). This inequality is a unique character of unary GBs since we would typically select the Gibbs dividing plane to ensure $\Gamma =0$ for other types of unary interfaces between two phases (e.g., unary solid-liquid and solid-vapor interfaces), so that ${s}_{{{{{{\rm{GB}}}}}}}^{{{{{{\rm{eff}}}}}}.}={s}^{{{{{{\rm{xs}}}}}}}$ for those cases. For an unary GB, ${s}_{{{{{{\rm{GB}}}}}}}^{{{{{{\rm{eff}}}}}}.}$ is typically positive because the GB region is usually more disordered (${s}^{{{{{{\rm{xs}}}}}}} \, > \, 0$) and less dense ($\Gamma \, < \, 0$ and $\Delta {v}_{{{{{{\rm{GB}}}}}}{{{{{\rm{free}}}}}}} \, > \, 0$) than the crystal. This suggests that GB energy generally decreases with increasing temperature or $(\partial {\gamma }_{{{{{{\rm{GB}}}}}}}/\partial T)_{P} \, < \, 0$ for a unary GB, as evident by the atomistic simulation of a Ni GB by Foiles (Fig. 1a)²¹. If a first-order GB premelting transition occurs, a “liquid-like” GB complexion²² (a.k.a. 2D interfacial phase) with a high ${s}_{{{{{{\rm{GB}}}}}}}^{{{{{{\rm{eff}}}}}}.}$ can form (Fig. 1a).

For a multicomponent system, the Gibbs-Duhem equation states:

$$\mathop{\sum }\limits_{i=1}^{N}{X}_{i}^{{{{{{\rm{bulk}}}}}}}d{\mu }_{i}=-\bar{S}dT+\overline{V}dP,$$

(5)

Combining Eqs. (2) and (5) at a constant pressure (dP = 0) produces:

$$d{\gamma }_{{{{{{\rm{GB}}}}}}}=-\Bigg[{s}^{{{{{{\rm{xs}}}}}}}-\Bigg(\frac{{\Gamma }_{1}}{{X}_{1}^{{{{{{\rm{bulk}}}}}}}}\Bigg)\bar{S}\Bigg]dT-\mathop{\sum }\limits_{i=2}^{N}\Bigg[{\Gamma }_{i}-\Bigg(\frac{{X}_{i}^{{{{{{\rm{bulk}}}}}}}}{{X}_{1}^{{{{{{\rm{bulk}}}}}}}}\Bigg){\Gamma }_{1}\Bigg]d{\mu }_{i}.$$

(6)

Here, we note that for multicomponent systems, chemical potentials (${\mu }_{i}$’s) depend on both temperature and the bulk composition (${X}_{i}^{{{{{{\rm{bulk}}}}}}}$). For an ideal solution, we can obtain:

$${\Bigg(\frac{\partial {\gamma }_{{{{{{\rm{GB}}}}}}}}{\partial {X}_{i}^{{{{{{\rm{bulk}}}}}}}}\Bigg)}_{P,T,{X}_{j}(j\ne 1;j\ne i)} =-\frac{RT}{{X}_{i}^{{{{{{\rm{bulk}}}}}}}}\Bigg[{\Gamma }_{i}-\Bigg(\frac{{X}_{j}^{{{{{{\rm{bulk}}}}}}}}{{X}_{1}^{{{{{{\rm{bulk}}}}}}}}\Bigg){\Gamma }_{1}\Bigg] \\ =-RT\Bigg[\frac{{\Gamma }_{i}}{{X}_{i}^{{{{{{\rm{bulk}}}}}}}}-\frac{{\Gamma }_{1}}{{X}_{1}^{{{{{{\rm{bulk}}}}}}}}\Bigg].$$

(7)

where R is gas constant. Taking Component 1 as the principal element (in a conventional multicomponent alloy), Eq. (7) suggests that increasing amount of segregation (${\Gamma }_{i} \, > \, 0$, while ${\Gamma }_{1} \, < \, 0$) can reduce GB energy ${\gamma }_{GB}$. This is illustrated by a binary example of Bi-doped Ni in Fig. 1b, which further shows the occurrence of a first-order GB adsorption transition that accelerates the GB energy reduction with increasing doping²³.

Let us consider the temperature dependence of GB energy, where we can treat two limiting cases. First, for a fixed bulk composition (i.e., below the solvus or solubility limit for all components), applying the chain rule to Eq. (2) produces:

$${\Bigg(\frac{\partial {\gamma }_{{{{{{\rm{GB}}}}}}}}{\partial T}\Bigg)}_{P,{{{{{{\bf{X}}}}}}}^{{{{{{\bf{b}}}}}}{{{{{\bf{u}}}}}}{{{{{\bf{l}}}}}}{{{{{\bf{k}}}}}}}({X}_{j}^{{{{{{\rm{bulk}}}}}}},j=1,2,{{{{\mathrm{..}}}}}.,N)} \, = \, -{s}^{{{{{{\rm{xs}}}}}}}-\mathop{\sum }\limits_{i=1}^{N}{\Gamma }_{i}{\Bigg(\frac{\partial {\mu }_{i}}{\partial T}\Bigg)}_{P,{{{{{{\bf{X}}}}}}}^{{{{{{\bf{b}}}}}}{{{{{\bf{u}}}}}}{{{{{\bf{l}}}}}}{{{{{\bf{k}}}}}}}} \, \\ = \, -\Bigg({s}^{{{{{{\rm{xs}}}}}}}-\mathop{\sum }\limits_{i=1}^{N}{\Gamma }_{i}{\bar{S}}_{i}\Bigg),$$

(8)

where ${\bar{S}}_{i}$ is the partial molar entropy of the i-th component, and X^bulk is bolded to represent the bulk composition vector of a multicomponent alloy). For a strong segregating system, GB energy often increases with increasing temperature because of temperature-induced desorption that reduces ${\gamma }_{{{{{{\rm{GB}}}}}}}$ (at least in the lattice model presented here without considering GB structural disordering, the effects of which can potentially reverse this trend and will be discussed later), thereby resulting in a negative effective ${s}_{{{{{{\rm{GB}}}}}}}^{{{{{{\rm{eff}}}}}}.\,({{{{{\rm{fixed}}}}}}\,{{{{{{\bf{X}}}}}}}^{{{{{{\bf{b}}}}}}{{{{{\bf{u}}}}}}{{{{{\bf{l}}}}}}{{{{{\bf{k}}}}}}})}$ (while ${s}^{{{{{{\rm{xs}}}}}}}$ can still be positive).

Second, we may consider a case of a saturated conventional multicomponent alloy with one principal and ($N-1$) segregating solute components. Here, with changing temperature, the composition of the grains moves along the maximum solvus line, where the chemical potentials of all solutes are pinned by a set of $(N-1)$ precipitates (assumed, for simplicity, to be stoichiometric line compounds). If chemical potentials ${\mu }_{j}$ (j ≠ 1) are fixed (as an approximation), we can derive from Eq. (6):

$${\Bigg(\frac{\partial {\gamma }_{GB}}{\partial T}\Bigg)}_{P,{X}_{j}(T) \, {{{{{\rm{on}}}}}} \, {{{{{\rm{solvus}}}}}}} \approx {\Bigg(\frac{\partial {\gamma }_{GB}}{\partial T}\Bigg)}_{P,{\mu }_{j}(j\ne 1)}\, \\ = \, -\Bigg[{s}^{{{{{{\rm{xs}}}}}}}-\Bigg(\frac{{\Gamma }_{1}}{{X}_{1}^{{{{{{\rm{bulk}}}}}}}}\Bigg)\bar{S}\Bigg]\equiv -{s}_{{{{{{\rm{GB}}}}}}}^{{{{{{\rm{eff}}}}}}.\,({{{{{\rm{saturated}}}}}})}.$$

(9)

For a segregating system, ${s}_{{{{{{\rm{GB}}}}}}}^{{{{{{\rm{eff}}}}}}.\,({{{{{\rm{saturated}}}}}})}$ is likely positive since we typically expect: ${s}^{{{{{{\rm{xs}}}}}}}$ > 0 and ${\Gamma }_{1}$ < 0.

GB high-entropy effects in a simplified segregation model

To illustrate GB and bulk high-entropy effects, we can use a statistical thermodynamic model for multicomponent GB segregation (a.k.a. adsorption)⁸ that is a generalization of the binary Wynblatt-Chatain model²⁴ with a few simplifications. Considering a general twist GB with segregation limited to the two layers at the GB core and further assuming an ideal solution for simplicity (that can be further refined to include multilayer adsorption and regular-solution interactions⁸), we can obtain:

$$\left\{\begin{array}{c}{\gamma }_{{{{{{\rm{GB}}}}}}}={\gamma }_{{{{{{\rm{GB}}}}}}}^{(0)}+2{n}_{{{{{{\rm{PD}}}}}}}\mathop{\sum }\limits_{i=2}^{N}{X}_{i}^{{{{{{\rm{GB}}}}}}}\Delta {g}_{i\to 1}^{{{{{{\rm{seg}}}}}}.}+2{n}_{{{{{{\rm{PD}}}}}}}\mathop{\sum }\limits_{i=1}^{N}kT{X}_{i}^{{{{{{\rm{GB}}}}}}}\,{{{{\mathrm{ln}}}}}\Bigg(\frac{{X}_{i}^{{{{{{\rm{GB}}}}}}}}{{X}_{i}^{{{{{{\rm{bulk}}}}}}}}\Bigg)\hfill\\ \frac{{X}_{i}^{{{{{{\rm{GB}}}}}}}}{{X}_{i}^{{{{{{\rm{bulk}}}}}}}}=\frac{{X}_{1}^{{{{{{\rm{GB}}}}}}}}{{X}_{1}^{{{{{{\rm{bulk}}}}}}}}\exp \Bigg(-\frac{\Delta {g}_{i\to 1}^{{{{{{\rm{seg}}}}}}.}}{kT}\Bigg)\hfill\end{array},\right.$$

(10)

where ${\gamma }_{{{{{{\rm{GB}}}}}}}^{(0)}$ is the GB energy of the pure Component 1, ${n}_{{{{{{\rm{PD}}}}}}}$ is the planar density of atoms, and $\Delta {g}_{i\to 1}^{{{{{{\rm{seg}}}}}}.}$ is the free energy change of GB segregation by swapping an atom of the i-th element inside the grain with an atom of the 1st element at the GB. Here, we adopt the sign convention that $\Delta {g}_{i\to 1}^{{{{{{\rm{seg}}}}}}.}=\Delta {h}_{i\to 1}^{{{{{{\rm{seg}}}}}}.}-T\Delta {s}_{i\to 1}^{{{{{{\rm{seg}}}}}}.}\approx \Delta {h}_{i\to 1}^{{{{{{\rm{seg}}}}}}.}$ < 0 for positive GB segregation (while noting that positive $\Delta {h}_{i\to 1}^{{{{{{\rm{seg}}}}}}.}$ values are sometimes cited in literature for GB enrichment). While we recognize the importance of GB segregation entropy $\Delta {s}_{i\to 1}^{{{{{{\rm{seg}}}}}}.}$^25,26,27, it produces a temperature-independent segregation term (Eq. (10)) that affect $\partial {\gamma }_{GB}/\partial T$ only indirectly. Thus, we focus on $\Delta {h}_{i\to 1}^{{{{{{\rm{seg}}}}}}.}$ (that is normally the larger and dominating term in $\Delta {g}_{i\to 1}^{{{{{{\rm{seg}}}}}}.}$) here and will discuss $\Delta {s}_{i\to 1}^{{{{{{\rm{seg}}}}}}.}$ (that were elaborated by Lejček et al.^25,26,27) latter. We also note that this model does not consider interfacial structural disorder so that ${\gamma }_{{{{{{\rm{GB}}}}}}}^{(0)}$ is independent of temperature (albeit it should exhibit a negative temperature dependence due to interfacial disordering and GB free volume, as shown in Fig. 1a and Eq. (3)). Equation (10) suggests no “high-entropy effect” for ${s}_{{{{{{\rm{GB}}}}}}}^{{{{{{\rm{eff}}}}}}.\,({{{{{\rm{fixed}}}}}}\,{{{{{{\bf{X}}}}}}}^{{{{{{\bf{b}}}}}}{{{{{\bf{u}}}}}}{{{{{\bf{l}}}}}}{{{{{\bf{k}}}}}}})}$ (that is likely negative due to temperature-induced desorption) in this model without considering GB disordering: e.g., in a simple analysis assuming $(N-1)$ segregating solutes of a fixed total amount of solutes ${\sum }_{i=2}^{N}{X}_{i}^{{{{{{\rm{bulk}}}}}}}$ and identical $\Delta {h}_{i\to 1}^{{{{{{\rm{seg}}}}}}.}$ (and therefore ${X}_{i}^{{{{{{\rm{GB}}}}}}}/{X}_{i}^{{{{{{\rm{bulk}}}}}}}$), both ${\gamma }_{{{{{{\rm{GB}}}}}}}$ and ${s}_{{{{{{\rm{GB}}}}}}}^{{{{{{\rm{eff}}}}}}.\,({{{{{\rm{fixed}}}}}}\,{{{{{{\bf{X}}}}}}}^{{{{{{\bf{b}}}}}}{{{{{\bf{u}}}}}}{{{{{\bf{l}}}}}}{{{{{\bf{k}}}}}}})}$are independent of N. However, ${s}_{{{{{{\rm{GB}}}}}}}^{{{{{{\rm{eff}}}}}}.\,({{{{{\rm{saturated}}}}}})}$can be positive and increase with increasing N.

To analytically illustrate a GB high-entropy effect in a dilute multicomponent alloy, we can analyze a hypothetic ideal solution with one principal (M) and $(N-1)$ segregating solute (S_i) elements (i.e., the bulk phase is not a HEA, referred to as “Type I” here). For a saturated N-component alloy in an equilibrium with $(N-1)$ precipitates (i.e., the bulk composition moves along the maximum solvus line following ${X}_{i,{{{{{\rm{slovus}}}}}}}^{{{{{{\rm{bulk}}}}}}}\approx \exp (\Delta {g}_{i}^{{{{{{\rm{sol}}}}}}./{{{{{\rm{ppt}}}}}}.}/kT)$ for $i=2,3,{{{{\mathrm{..}}}}}.,N$, where $\Delta {g}_{i}^{{{{{{\rm{sol}}}}}}./{{{{{\rm{ppt}}}}}}.}$ < 0 is the free energy of dissolving i from the precipitate), we can derive an approximated expression at the dilute limit (${\sum }_{i=2}^{N}{X}_{i}^{{{{{{\rm{bulk}}}}}}} < < 1$) as:

$$\left\{\begin{array}{c}\frac{{X}_{i}^{{{{{{\rm{GB}}}}}}}}{{X}_{1}^{{{{{{\rm{GB}}}}}}}}\approx \exp \Bigg(-\frac{\Delta {g}_{i}^{{{{{{\rm{seg}}}}}}.-{{{{{\rm{ppt}}}}}}.}}{kT}\Bigg)\hfill\\ {\gamma }_{{{{{{\rm{GB}}}}}}}-{\gamma }_{{{{{{\rm{GB}}}}}}}^{(0)}\approx 2{n}_{{{{{{\rm{PD}}}}}}}kT\,{{{{\mathrm{ln}}}}}\,{X}_{1}^{{{{{{\rm{GB}}}}}}}\approx -2{n}_{{{{{{\rm{PD}}}}}}}kT\,{{{{\mathrm{ln}}}}}\Bigg[1+\mathop{\sum }\limits_{i=2}^{N}\exp \Bigg(-\frac{\Delta {g}_{i}^{{{{{{\rm{seg}}}}}}.-{{{{{\rm{ppt}}}}}}.}}{kT}\Bigg)\Bigg]\hfill\end{array},\right.$$

(11)

where $\Delta {g}_{i}^{{{{{{\rm{seg}}}}}}.-{{{{{\rm{ppt}}}}}}.}$ (=$\Delta {g}_{i\to 1}^{{{{{{\rm{seg}}}}}}.}-\Delta {g}_{i}^{{{{{{\rm{sol}}}}}}./{{{{{\rm{ppt}}}}}}.}$) represents the free energy difference between the segregation and precipitation per atom. Here, an empirical relationship (for the enthalpic part) exists: $\Delta {g}_{i}^{{{{{{\rm{seg}}}}}}.-{{{{{\rm{ppt}}}}}}.}$ ≈ $-(0.10\,{{\pm }}\,0.06)$ eV/atom (or ${-}(10\,{{\pm }}\,6)$ kJ/mol)²⁸. Equation (11) suggests that adding more segregating elements can reduce ${\gamma }_{GB}$ along the solvus line for a N-component system (i.e., increase the effective GB entropy ${s}_{{{{{{\rm{GB}}}}}}}^{{{{{{\rm{eff}}}}}}.\,({{{{{\rm{saturated}}}}}})}$), representing a GB high-entropy effect.

Furthermore, we can conduct numerical experiments to show this GB high-entropy effect using typical parameters for transition metals (using similar parameters as the case shown in Fig. 6 in Ref. ⁸, but for a simpler ideal solution in an equilibrium with $(N-1)$ precipitates of 1:1 stoichiometric (M)₁(S_i)₁ of identical (significant)$\Delta {g}_{i}^{{{{{{\rm{sol}}}}}}./{{{{{\rm{ppt}}}}}}.}$ of $-0.13$ eV/atom and an intermediate $\Delta {g}_{i\to 1}^{{{{{{\rm{seg}}}}}}.}$ similar to those for Nb or Ta in Ni). Figure 2a shows this GB high-entropy effect of enhanced reduction in ${\gamma }_{GB}$ with more segregating elements. Similar results were obtained in a regular-solution model previously⁸.

Fig. 2: Grain boundary (GB) and bulk high-entropy effects in high-entropy grain boundaries (HEGBs).

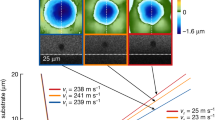
a Computed normalized GB energy (${\gamma }_{{GB}}/{\gamma }_{{GB}}^{(0)}$) vs. temperature ($T$) curves showing that a GB high-entropy effect can decrease $d{\gamma }_{{GB}}/{dT}$ along the solvus line in a hypothetic conventional multicomponent nanoalloy with one principal (M) and multiple segregating (S_i) elements. This GB high-entropy effect increases with increasing number of segregating elements. b Computed ${\gamma }_{{GB}}/{\gamma }_{{GB}}^{(0)}$ vs. $T$ curves along the bulk solvus curves, showing that ${{\gamma }}_{{GB}}$ can also be reduced via a bulk high-entropy effect that lower the bulk chemical potentials to suppress precipitation to promote GB adsorption for a hypothetic high-entropy nanoalloy of 1–5 principal (M_i) and one segregating element (S). In (a and b), subscript “S” indicates the bulk composition of the segregating element is kept saturated (on the solvus line) at each temperature. c Computed ${\gamma }_{{GB}}/{\gamma }_{{GB}}^{(0)}$) vs. $T$ curves for several “Ni-like” alloys, where the superscripts “^*” are used note that the calculations were conducted by using a lattice model of ideal solutions with segregation enthalpies and bonding energies mimic the real alloys to capture useful trends. d Selected experimental results of measured grain sizes of nanoalloys annealed at three different temperatures for 5 h, which shows a correlation between reduced GB energies and grain sizes. e Experimentally measured grain size vs. annealing temperature curves for several nanoalloys with HEGBs along with Ni and Ni-based binary nanoalloys for comparison⁹. The numerical and experimental results are replotted or regenerated using the same procedures; the figure panels are reprinted or replotted after Zhou et al.^{8, 9}, both with permission ©Elsevier 2016.

Bulk high-entropy effects and type II HEGBs

In addition, we can show a bulk high-entropy effect for HEAs with multiple principal elements (i.e., the grains are HEAs) and at least one (or more) segregating elements to form “Type II” HEGBs (Fig. 2b)⁹. Prior numerical experiments (Fig. 2b)⁹ of a hypothetic symmetric ideal solution with $(N-1)$ principal (M_i, assumed to have identical properties for simplicity) and one (S) segregating elements based on the same model described above illustrate that ${\gamma }_{GB}$ can also be reduced via a bulk high-entropy effect. This bulk high-entropy effect lowers the bulk chemical potentials to suppress precipitation to promote more GB adsorption for the HEAs saturated with the segregating element S. Moreover, increasing the number of principal elements in HEAs enhances this bulk high-entropy effect to attain more negative ${(\partial {\gamma }_{GB}/\partial T)}_{{{{{{\rm{saturated}}}}}}}$, as shown in Fig. 2b. Similar to the prior case, we can also derive an approximated analytical expression for an ideal solution at the dilute limit (${X}_{N}^{{{{{{\rm{bulk}}}}}}} < < 1$; ${X}_{i}^{{{{{{\rm{bulk}}}}}}}=(1-{X}_{N}^{{{{{{\rm{bulk}}}}}}})/(N-1)\approx 1/(N-1)$ for $\,i=1,2, {.}..,(N-1)$) for a Type II HEGB in a HEA:

$${\gamma }_{{{{{{\rm{GB}}}}}}}-{\gamma }_{{{{{{\rm{GB}}}}}}}^{(0)}\approx 2nkT \, {{{{{\mathrm{ln}}}}}}\left(\frac{{X}_{1}^{{{{{{\rm{GB}}}}}}}}{{X}_{1}^{{{{{{\rm{bulk}}}}}}}}\right) \approx -2{n}_{{{{{{\rm{PD}}}}}}}kT \, {{{{{\mathrm{ln}}}}}}\left[1+{(N-1)}^{x/y}\exp \left(-\frac{{\Delta} {g}_{N}^{{{{{{\rm{seg.}}}}}}-{{{{{\rm{ppt.}}}}}}}}{kT}\right)\right].$$

(12)

Here we assume, for simplicity, all binary i-N systems ($\,i=1,2,{{{{\mathrm{.}}}}}..,(\it N-1)$) have identical thermodynamic parameters and the binary solvus lines are pinned by stoichiometric (M_i)_x(S)_y precipitates following ${X}_{i,\,{{{{{\rm{binarysolvus}}}}}}}^{{{{{{\rm{bulk}}}}}}}\approx \exp (\Delta {g}_{N}^{{{{{{\rm{sol}}}}}}./{{{{{\rm{ppt}}}}}}.}/kT)$, so that the bulk solubility limit of the segregating N-th component is given by: ${X}_{N}^{{{{{{\rm{bulk}}}}}}}={(N-1)}^{x/y}\exp (\Delta {g}_{N}^{{{{{{\rm{sol}}}}}}./{{{{{\rm{ppt}}}}}}.}/kT)$. Equation (12) suggests that more principal elements can also reduce ${\gamma }_{GB}$ along the solvus line (i.e., increase the effective GB entropy ${s}_{{{{{{\rm{GB}}}}}}}^{{{{{{\rm{eff}}}}}}.\,({{{{{\rm{saturated}}}}}})}$). This represents a bulk high-entropy effect for Type II HEGBs with HEA grains.

We should note that this bulk high-entropy effect and Type II HEGBs may also exist in conventional HEAs if one (or more) of the principal element(s) segregates at GBs. An assessment by Miracle and Senkov³ suggested that slow bulk diffusion in HEAs may not supported by the available data; in fact, the term “sluggish kinetics” was initially introduced based on the observations of fine grains in HEAs. Here, we hypothesize that the “sluggish” grain growth kinetics can exist HEAs because of this bulk high-entropy effect (with the formation of Type II HEGBs), which should be further examined in future studies.

Interfacial structural disordering and GB transitions

The segregation model discussed above do not consider GB structural disordering, which can further increase GB entropy. In addition, first-order GB transitions (e.g., a first-order GB segregation transition for Ni-Bi²⁹ shown Fig. 1b and a hypothetic first-order GB premelting transition shown in Fig. 1a) can take place to accelerate the reduction in ${\gamma }_{GB}$. GB structural disordering and segregation can be coupled, as observed in W-Ni (Fig. 1c)³⁰. It is yet unknown when (and why) ordered (Ni-Bi)²⁹ vs. disordered (W-Ni)³⁰ segregation structures form at GBs. We anticipate that structurally disordered HEGBs can possess even higher effective GB entropies with increased interfacial width (Fig. 1c) and potentially exhibit positive ${s}_{{{{{{\rm{GB}}}}}}}^{{{{{{\rm{eff}}}}}}.\,({{{{{\rm{fixed}}}}}}\,{{{{{{\bf{X}}}}}}}^{{{{{{\bf{b}}}}}}{{{{{\bf{u}}}}}}{{{{{\bf{l}}}}}}{{{{{\bf{k}}}}}}})}$ (that is negative at a fixed grain composition in the lattice model discussed above that does not consider GB disordering effect) to show GB high-entropy effects. This is an area that is largely unexplored and will be discussed further in the Outlook section.

Definitions and terminologies

Similar to bulk HEAs, the definition of HEGBs can be debatable. Here, we propose to first define “compositionally complex GBs (CCGBs)” as GBs with at least five principal components (e.g., >5%) at the GB core, as the GB counterpart to the bulk CCAs or CCCs. Then, we may loosely define HEGBs as the GBs with large, positive effective GB entropy (${s}_{{{{{{\rm{GB}}}}}}}^{{{{{{\rm{eff}}}}}}.}\equiv -\partial {\gamma }_{GB}/\partial T$). It is important to note that effective ${s}_{{{{{{\rm{GB}}}}}}}^{{{{{{\rm{eff}}}}}}.}$ can be either positive and negative in multicomponent alloys (vs. bulk configurational entropy that is always positive), and it also depends on the bulk phase equilibrium condition (e.g., fixed grain composition vs. saturated with secondary precipitation phases: ${s}_{{{{{{\rm{GB}}}}}}}^{{{{{{\rm{eff}}}}}}.\,({{{{{\rm{fixed}}}}}}\,{{{{{{\bf{X}}}}}}}^{{{{{{\bf{b}}}}}}{{{{{\bf{u}}}}}}{{{{{\bf{l}}}}}}{{{{{\bf{k}}}}}}})}$ ≠${s}_{{{{{{\rm{GB}}}}}}}^{{{{{{\rm{eff}}}}}}.\,({{{{{\rm{saturated}}}}}})}$). At this time, we are reluctant to suggest a specific cut-off value in ${s}_{{{{{{\rm{GB}}}}}}}^{{{{{{\rm{eff}}}}}}.}$ to define HEGBs (that would be highly subjective). Instead, we propose two essential characters that help to define HEGBs: (1) the effective ${s}_{{{{{{\rm{GB}}}}}}}^{{{{{{\rm{eff}}}}}}.}\equiv -\partial {\gamma }_{GB}/\partial T$ of HEGBs should be positive and (2) it should increase with increasing number of (segregating and/or primary) components, which can be achieved via the GB and/or bulk high-entropy effects discussed above.

Unlike the bulk phases, more principal components at the GB core (in CCGBs) do not always lead to larger (or even positive) ${s}_{{{{{{\rm{GB}}}}}}}^{{{{{{\rm{eff}}}}}}.}\equiv -\partial {\gamma }_{GB}/\partial T$ for GBs. The configurational entropy at the GB core and the effective GB entropy (${s}_{{{{{{\rm{GB}}}}}}}^{{{{{{\rm{eff}}}}}}.}$) are not always positively correlated. In fact, CCGBs (in both HEAs and conventional multicomponent alloys) can have negative ${s}_{{{{{{\rm{GB}}}}}}}^{{{{{{\rm{eff}}}}}}.}$ so that they cannot be considered as HEGBs even if there are five or more components of nearly equimolar fractions at the GB core.

These unique characters (somewhat differing from bulk CCAs vs. HEAs) make the thermodynamics of CCGBs and HEGBs intriguing and interesting, calling for further theoretical, modeling, and experimental studies.

Stabilizing nanoalloys at high-temperatures via HEGBs

While HEGBs may have several unique characters, one potential application is to utilize them to stabilize nanoalloys at high temperatures⁹. To test this, we modeled, and subsequently fabricated and tested, several Type I (e.g., Ni_79.5Ta_5.5Nb₁₀W₅) and Type II (e.g., Ni₂₉Fe₂₃Co₂₃Cr₂₃Zr₂) multicomponent nanoalloys to show substantially improved high-temperature stability (Fig. 2c–e)⁹.

Here, we can simulate multicomponent alloys via adopting (1) the above simplified GB segregation model, (2) estimated GB and bonding energies as well as $\Delta {g}_{i\to 1}^{{{{{{\rm{seg}}}}}}.}$ for the actual alloys, and (3) binary solvus lines based on empirical $\Delta {g}_{i}^{{{{{{\rm{seg}}}}}}.-{{{{{\rm{ppt}}}}}}.}$ or experimental phase diagrams to forecast useful trends⁹. Here, we use subscript “*” (e.g., “Ni*₂₅Fe*₂₃Co*₂₃Cr*₂₃Mo*₂Nb*₂Zr*₂”) to denote that they are ideal solutions that mimic the real alloys. Figure 2c suggests both GB and bulk high-entropy effects in reducing ${\gamma }_{GB}$, in comparison with benchmarks, for several alloys⁹. Subsequent experiments found that both Type I and Type II nanoalloys with HEGBs exhibit improved (sometime superior) high-temperature stabilities⁹. For example, Ni₂₅Fe₂₃Co₂₃Cr₂₃Mo₂Nb₂Zr₂ (with four principal and three segregating elements) maintained ~45 nm grain size after 5 h annealing at 1000 °C, outperforming not only their binary counterparts (Ni₇₉Zr₂₁ and Ni₉₃Zr₇) but also the conventional HEA counterpart (Ni₂₅Fe₂₅Co₂₅Cr₂₅), as shown in Fig. 2d, e⁹. This modeling and experimental validation methodology can be extended to other alloys in future studies.

We should note that there are two general approaches to inhibit grain growth: (1) thermodynamic stabilization by reducing ${\gamma }_{GB}$ via solute segregation can reduce the grain growth driving force and (2) kinetic stabilization by solute drag and/or Zener (particle) pinning^{31, 32}. Notably, in the cases shown in Fig. 2c, GB energies, although being reduced by the HEGBs, are still significant (non-zero). Thus, kinetic stabilization should exist and be important.

A Ni₈₀Mo_6.6Ti₆Nb₆Ta_1.4 alloy was designed to further examine kinetic effects, where the Ti, Nb and Ta contents were about 60–70% of the binary solvus at 900 °C while Mo was ~25% of binary solid solubility⁹. Thus, this case resembles the fixed bulk composition scenario represented by Eq. (8) with no or little anticipated GB high-entropy effect (or the GBs in Ni₈₀Mo_6.6Ti₆Nb₆Ta_1.4 are CCGBs but not HEGBs). However, a prior experiment showed that this nanoalloy possessed a superior high-temperature stability, maintaining 45 nm grain size after annealing 1000 °C for 5 h (Fig. 3d, e)⁹. Here, the kinetic effects, particularly solute drag^{33, 34} (since binary phase diagrams suggest no precipitate above ~700 °C), presumably played the key role in stabilizing this nanoalloy.

Fig. 3: Stabilizing nanoalloys at high temperatures with high-entropy grain boundaries (HEGBs).

Schematic illustration of a balance of reduced thermodynamic driving pressure (${\gamma }_{{{{{{\rm{GB}}}}}}}/\left\langle d\right\rangle$, where ${\gamma }_{{{{{{\rm{GB}}}}}}}$ is grain boundary energy and $\left\langle d\right\rangle$ is the mean grain size) and increased critical kinetic solute drag pressure (${{P}_{C}}^{{{{{{\rm{drag}}}}}}}$) for grain growth, which result in the stabilization of a nanoalloy against grain growth. This balance has to be achieved before precipitation (below the solubility limit if the nanoalloy is at a thermodynamic equilibrium). Increasing temperature (T) can induce GB desorption (de-segregation) that moves the balance point toward right (to de-stabilize the nanoalloy, albeit the solubility limits also increase with increasing temperature). The HEGB-stabilized grain boundary segregation can counter the thermally induced desorption. The increased total adsorption (the total amount of all segregating components) at HEGBs, which can be more stable at high temperatures with increasing number of components, can simultaneously reduce the thermodynamic driving force and increase the kinetic solute drag, thereby increasing the high-temperature stability (or moving the balance point toward left). Interfacial disordering (illustrated in Fig. 1c) can further alter the thermodynamic and kinetic stabilities of nanoalloys at high temperatures.

Figure 3 shows that a stable nanoalloy can be achieved via a balance between the thermodynamic driving pressure (${\gamma }_{GB}/\langle d\rangle$, where $\langle d\rangle$is the mean grain size) and critical kinetic solute-drag pressure (${{P}_{C}}^{{{{{{\rm{drag}}}}}}}$, i.e., the maximum drag force solutes can imposed on the GB before it tears itself off in the Cahn-Lücke-Stüwe model^{33, 34}): ${\gamma }_{GB}/\langle d\rangle$= ${{P}_{C}}^{{{{{{\rm{drag}}}}}}}$. However, both the thermodynamic stabilization and kinetic solute drag become less effective at high temperatures due to temperature-induced GB desorption, which moves the balance point in Fig. 3 toward right. Here, HEGBs may boost GB adsorption to counter the thermally induced desorption (to move the balance point in Fig. 3 toward left to allow a larger stable window). Specifically, HEGBs can accommodate a higher total amount of GB adsorption within the bulk solid solubility limit (enhanced at high temperatures with more components, as shown in Fig. 2a, b). This effect can not only reduce the thermodynamic driving force for grain growth by decreasing ${\gamma }_{GB}$ at high temperatures, but also enlarge solute drags to pin grain growth kinetically in “sluggish” HEGBs. We recognize that Zener (particle) pinning is another kinetic stabilization effect (not yet considered in Fig. 3).

Outlook

The theory of HEGBs is still in its infancy stage. Although the concept of HEGBs was proposed in 2016 with some modeling and experimental supports^{8, 9}, which has caught substantial interests since then^{10,11,12,13,14,15,16,17,18,19,20, 25, 35, 36}, this current article is the first comprehensive discussion of the underlying thermodynamic theory (yet with simplified models). Thermodynamic and kinetic models of HEGBs should be developed and improved to guide this exploration and enable rigorous data analysis.

The multicomponent segregation model presented here, although they can illustrate important concepts and predict some useful trends, is highly simplified. Here, several improvements should be made in future studies. First, multilayer segregation and regular-solution interactions can be readily included, but analysis of a multicomponent system posts a challenge. For a $N$-component system, there are $N\times (N-1)/2$ regular-solution (pair-interaction) parameters, e.g., there will be 10 pair-interaction parameters for a 5-component system! This will lead to complex (yet interesting) phenomena that should simulate future studies. Second, such pair interactions can result in ordering and clustering at GBs (as shown, e.g., in a recent study of GBs in HEAs³⁷), which can reduce the configurational entropy at GBs. Third, GB segregation entropy ($\Delta {s}_{i\to 1}^{{{{{{\rm{seg}}}}}}.}$)^25,26,27 should also be considered to better model GB segregation. Here, we note that GB segregation entropy ($\Delta {s}_{i\to 1}^{{{{{{\rm{seg}}}}}}.}$) and the effective GB entropy (${s}_{{{{{{\rm{GB}}}}}}}^{{{{{{\rm{eff}}}}}}.}\equiv -\partial {\gamma }_{GB}/\partial T$) are two important GB-related entropies with different meanings. This Perspective article discusses the latter (${s}_{{{{{{\rm{GB}}}}}}}^{{{{{{\rm{eff}}}}}}.}$), but we recognize that GB segregation entropy ($\Delta {s}_{i\to 1}^{{{{{{\rm{seg}}}}}}.}$) can play an important role in determining GB segregation behaviors (thereby affecting $\partial {\gamma }_{GB}/\partial T=-{s}_{{{{{{\rm{GB}}}}}}}^{{{{{{\rm{eff}}}}}}.}$, albeit somewhat indirectly as it produces a temperature-independent segregation according to Langmuir-MacLean type Eq. (10)). Interested readers are referred to Prof. Lejček et al.’ articles^25,26,27 for in-depth discussion of GB segregation entropy ($\Delta {s}_{i\to 1}^{{{{{{\rm{seg}}}}}}.}$).

Moreover, GB structural disordering, which is not considered in this segregation model, offers a further opportunity to attain even higher effective GB entropies. For example, while the lattice segregation model without considering interfacial disordering suggests no GB high-entropy effect for the fixed grain composition scenario (${s}_{{{{{{\rm{GB}}}}}}}^{{{{{{\rm{eff}}}}}}.\,({{{{{\rm{fixed}}}}}}\,{{{{{{\bf{X}}}}}}}^{{{{{{\bf{b}}}}}}{{{{{\bf{u}}}}}}{{{{{\bf{l}}}}}}{{{{{\bf{k}}}}}}})}$ < 0), coupled interfacial disordering and segregation of multiple species, which can enhance each other, may alter the high-temperature behaviors to allow decreasing ${\gamma }_{GB}$ (and increasing total adsorption amount) with increasing temperature even with a fixed grain composition (to allow ${s}_{{{{{{\rm{GB}}}}}}}^{{{{{{\rm{eff}}}}}}.\,({{{{{\rm{fixed}}}}}}\,{{{{{{\bf{X}}}}}}}^{{{{{{\bf{b}}}}}}{{{{{\bf{u}}}}}}{{{{{\bf{l}}}}}}{{{{{\bf{k}}}}}}})}$ > 0). This possibility (hypothesis) is yet to be tested by modeling and experiments. A more rigorous model of HEGBs should consider both chemical and structural (disordering) effects. Developing models for HEGBs in ceramics, which are more prone to form amorphous-like (structurally disordered) GBs³⁸, represents another challenge and opportunity.

Here, a future opportunity is to utilize GB disordering and transitions to tailor HEGBs and subsequently the high-temperature stability of nanoalloys (and other properties). Notably, Rupert’s group showed the formation of amorphous-like GBs in W-doped Ni³⁹, Cu-Zr-Hf⁴⁰, and most recently in Cu-Zr-Hf-Nb-Ti and similar quinary nanoalloys²⁰ that enhance their high-temperature stability. This suggests a possibility to form structurally disordered (amorphous-like) HEGBs with even higher GB entropies to further enable exceptional high-temperature nanoalloy stability and other exotic properties (e.g., improved mechanical properties with amorphous-like GBs^{41, 42}). Amorphous-like intergranular films, first discovered in W-Ni (Fig. 1c) and Mo-Ni for metals (as segregation-induced GB premelting or prewetting)^{30, 43}, which are more commonly observed in ceramics³⁸, can enable (accommodate) more adsorption. A series of other GB complexions (a.k.a. 2D interfacial phases)^{22, 29, 44,45,46,47} may also exist in HEGBs, leading to different properties and opportunities.

A recent report showed the feasibility of combining atomistic simulations and machine learning to predict GB segregation and GB disorder for HEAs in a 5D space (as functions of temperature and four independent compositional degrees of freedom for quinary alloys), where a key observation is the coupling of GB segregation and disordering (that may further increase the effective GB entropy as discussed about)⁴⁸. Such methods can be used to model HEGBs more realistically and accurately than simplified models. Notably, GB “phase” diagrams have been computed for binary, multicomponent, and high-entropy alloys, representing a potentially transformative research direction⁴⁹. We envision that such GB diagrams may also be constructed to represent the temperature- and composition-dependent formation of both classes of HEGBs, as well as their thermodynamic, structural, and other properties in future studies.

Notably, Weismuller proposed the existence of an “equilibrium” grain size when the effective ${\gamma }_{GB}$ approaches zero;⁵⁰ yet, Kirchheim⁵¹ suggested (based on the empirical relationship $\Delta {G}_{i}^{{{{{{\rm{seg}}}}}}.-{{{{{\rm{ppt}}}}}}.}$ ≈ ${-}(10\,{{\pm }}\,6)$ kJ/mol²⁸ that the equilibrium grain sizes in binary alloys often represent metastable states in supersaturated regions if and only if the precipitation is hindered kinetically, which also becomes difficult with increasing temperature. It is interesting to investigate whether truly equilibrium nanoalloys can exist in multicomponent alloys with HEGBs, which is suggested by Fig. 1a, but not yet verified experimentally.

Furthermore, a first-order premelting transition can result in a discontinuous increase in the GB excess entropy to accelerate the GB energy reduction with increasing temperature (Fig. 1a, albeit that studies showed GB structural disordering can often increase GB mobilities⁴⁴.). Likewise, a first-order adsorption transitions can also cause a discontinuous increase in the GB adsorption (a.k.a. segregation), which accelerates the GB energy reduction with increasing chemical potential (Fig. 2b)^{23, 29, 47}. It will be exciting to seek coupled GB disordering or adsorption transitions in HEGBs to further accelerate the ${\gamma }_{GB}$ reduction (i.e., increase the effective GB entropy) to potentially achieve zero GB energy within the solid solubility limit (to realize nanoalloys with equilibrium grain sizes at a true thermodynamic equilibrium).

We should develop quantitative models for the combined thermodynamic and kinetic stabilization of nanoalloys at high temperatures via utilizing HEGBs, following the concept shown in Fig. 3. We should also further explore the unique characters of HEGBs beyond thermodynamic and kinetic properties.

A further extension is to investigate other types of high-entropy interfaces beyond GBs. For example, can we use high-entropy surfaces to stabilize nanoparticles for high-temperature catalysis or other applications?⁵² Do high-entropy surfaces (or solid-solid heterointerfaces) have unique properties?