Introduction

Two-dimensional (2D) materials are attractive to the community for their unprecedented deformability and a variety of novel properties1,2,3,4. Similar to the bulk semiconductors, extensive efforts have been devoted to the strain engineering on 2D materials5,6. Including graphene and transition metal dichalcogenides (TMDs), the electronic band structures of 2D materials are prevalently sensitive to the external loading, leading to significant changes in electrical or optical properties7,8,9. It is more intriguing for the anisotropic 2D materials such as rhenium disulfide (ReS2), as the crystal lattice reconstructions and sub-domain structures can contribute an additional degree of freedom for control10,11,12.

According to the elasticity and plastic theory, stressing the three-dimensional (3D) bulk materials can result in a certain deformation in crystal lattices13. On the contrary, for 2D materials, which can be regarded as nearly ideal plane-stress deformation due to the vanishing thickness14,15, the induced strain could have higher uncertainties. For example, the out-of-plane undulation/rippling in 2D materials is almost unavoidable, especially under compressive or shear stress16. Such rippling is also intrinsic to stabilize the suspended 2D crystals17. On the other hand, 2D materials can usually be stressed close to the ideal strength due to the exclusion of atomic defects18, leaving the elasticity entering the deep nonlinear regime19. Indeed, abundant theories and experiments on the 2D materials such as graphene and 2D TMDs have shown their excellent mechanical properties, which also justify their great potentials in future applications20,21,22,23,24,25.

Compared to the isotropic 2D counterparts, less is known about the anisotropic 2D materials. It has been reported the 2D ReS2 or ReSe2 can undergo atomic lattice reconstruction under electron beam effect26. The 2D ReS2 after growth were also observed with stripe-like or needle-like domains and parallel domain boundaries, though the as-grown samples on the growing substrates without transfer have not been systematically investigated27,28. Apart from that, the anisotropic atomic structures (viz. the directional Re atomic chains, see Fig. 1a) in these T′ phases of 2D TMDs have also been manifested to have anisotropic electrical and optical properties22,28,29,30,31,32,33,34. The anisotropic high electron mobility and the hierarchical domain structure in ReS2 may create new possibilities for the property modulation in 2D structures.

Fig. 1: The martensite-like domain structures in 2D ReS2.
figure 1

a, b The color optical images under bright field, polarized 70° and 110° for CVD-grown 1L-ReS2 transferred on 300 nm SiO2/Si substrate, and mechanical exfoliated ReS2 on 300 nm SiO2/Si substrate, respectively. The inset shows the crystal structure model of monolayer (1L) ReS2 with chain-like structures (dashed black lines). c, d The DFM phase and topography images of monolayer ReS2 as grown on mica (ReS2/mica). e The magnified DFM topography image corresponding to the white dashed square in d. f The line profiles corresponding to the black dashed lines in e.

Full size image

It was explained that the sub-domain structures in 2D ReS2 exist with mirror (twin) boundaries27,34. However, the origin of these domains is not clear yet. As we will discuss in the current paper, the rich-domain structures in 2D ReS2 can be attributed to the atomic lattice reorganization under ultra-low strain. Here we will give a complete explanation for the origin of all the needle-like domain patterns with a complete list of domain boundary types. These observed domains are not originated during growth in the chemical vapor deposition (CVD) at high temperature (CVD-grown products are virtually single crystal for each flake from a single nuclei), rather they are attributed to the cool-down stress by sample-substrate thermal expansion differences. The rich-domain structures in 2D ReS2 are formed by lattice reorganization during the cooling process, which resembles the formation of the needle-like microstructure of martensite by iron atomic rearrangement during the cooling process35,36. Here the origin of “martensite-like” structures in anisotropic 2D ReS2 is investigated.

Results and discussion

The martensite-like domain structures in 2D ReS2

The monolayer and multilayer 2D ReS2 samples in our experiments were synthesized either by the CVD method or mechanical exfoliation method (see “Methods” section)37,38. Similar to previous reports, the CVD-grown monolayer (1L) ReS2 samples, irrespective of monolayer or multilayers, predominantly exhibited sub-domain structures and parallel stripe patterns under polarized optical microscopy (OM) (Fig. 1a). After the samples were wet-transferred (see “Methods” section) onto new substrates, the domain and stripe patterns persisted (Supplementary Fig. 1). Comparatively, the mechanical exfoliated 1L-ReS2 samples did not show any domain patterns above (Fig. 1b). We have verified the above patterns using dynamic force microscopy on the as-grown samples (DFM, see “Methods” section), in the topography images, the similar patterns can be clearly identified, while the phase images can further enhance the domain contrasts (Fig. 1c, the corresponding topography images show in Supplementary Fig. 2). Notably, the multilayer ReS2 also possess similar sub-domain structures irrespective of the thickness (Supplementary Fig. 3). These domain structures should be attributed to the different orientated crystal grains of 2D ReS2. Hence the DFM phase images can be understood—domain contrast came from the different molecular interactions between scanning tips and ReS2 surfaces along different crystal orientations. However, the brighter contrast half (higher) in the DFM topography image implies there is partial delamination between the 2D flake and substrate (Fig. 1d–f). Particularly, for the triangle flakes, the needle-like or stripe-like patterns are more likely to form in the undelaminated half flakes (the darker halves in the DFM topography images) than the delaminated half (the brighter halves in DFM topography images) (Fig. 1e), which will be explained later.

The strain distribution of the as-grown ReS2

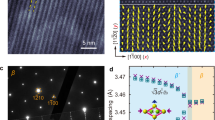
Here we used the angle-resolved polarized Raman (ARPR) spectroscopy39 to examine the 2D monolayer ReS2 samples without transfer (which means they are measured on the growth substrates directly). The polarized optics in our Raman setup has been verified on 1L-MoS2 prior to the measurement on ReS2 (Supplementary Figs. 4 and 5). We have correlated the Raman and DFM results for the same ReS2 flakes (CVD grown on fluorophlogopite mica) (see “Methods” section). Considering the anisotropic optical property of ReS2 and the non-polarized Raman measurement is less sensitive to anisotropic structures, the ARPR measurement is imperative for the in-plane anisotropic ReS2 (Fig. 2). In the DFM phase images, the brighter color contrast indicates the lattice reconstruction area and the darker color contrast indicates the delaminated area (Fig. 2a). The Raman peak at 3, 4, 5, and 6 (Fig. 2b) are the Re atoms in-plane vibration modes40. Different vibration modes in 1L-ReS2 are excited with different polarization directions. Besides, the ARPR intensity of peak 5 indicates the orientation of Re chain34. As shown in Fig. 2c, d, the intensities of Raman peak 5 exhibit stark differences between the delaminated/undelaminated domains. The Raman intensity variance can be explained by the different strain levels. The crystal orientations influence the angle of reaching maximum peak intensity (Fig. 2e, f). Peaks 3, 5, and 6 of sub-domain I reach maximum intensity at polarized angles 138°, 70°, and 65° (Fig. 2e). It shows a decreasing trend. On the contrary, the peaks 3, 5, and 6 of sub-domain II reach the maximum intensity at polarized angles 108°, 135°, and 150° (Fig. 2f). It shows an increasing trend. The inverse trend indicates the different lattice orientations (Fig. 2e, f). However, as for the orientation of each vibration mode, there are still huge intensity differences. As shown in Fig. 2g–i, the maximum peak intensity at peaks 3, 5, and 6 of sub-domain I are ~120, ~250, and ~250% of sub-domain II. The lattice reconstructed area has stronger APRP intensity than the delaminated area. The reduction of Raman intensity of ReS2 is owing to the existed strain41. Hence, the residual strain effects are verified by the difference of ARPR intensity at oriented directions. More strain is released in the lattice reconstructed area, leading to a higher ARPR intensity than the delaminated area.

Fig. 2: The ARPR characterizations on CVD-grown 2D 1L-ReS2.
figure 2

a The DFM phase image. b The single Raman spectra (polarized 0°) of 1L-ReS2 at different sub-domains corresponding to the blue and red spots in c. c, d The polarized 0° and polarized 90° Raman peak 5 intensity mapping, respectively. e, f Polarization-dependent Raman intensity mappings corresponding to the blue and red spots in c, respectively. g–i Angle-dependent polar plots for sub-domain I and sub-domain II at peaks 3, 5, 6 (scatter) and fitted by Sine function (line), respectively.

Full size image

Cooling-induced train at ReS2/substrate interface

The delamination of CVD as-grown flakes usually occurs during the cooling down process, so that the cooling rate is modulated to investigate the cool-down stress (Fig. 3). The slow-cooling rate produces less domain patterns on the sample (Fig. 3a, d), while the fast-cooling rate leads to more and denser domain patterns on 1L-ReS2 sample (Fig. 3c, f). Initially, the sub-domain structures observed under polarized 70° OM images (Fig. 3a–c) indicate the distinguishing Re chain orientations. Furthermore, the needle-like patterns are studied using the DFM topography and phase characterizations (Fig. 3d–f). The delaminated areas have brighter contrast (higher) in DFM topography images resulted from the release of the cool-down stress. On the other hand, the lattice reconstruction is the stress release of the undelaminated area. Apparently shown in DFM phase images, the delaminated area shows the darker contrast and the lattice reconstructed area shows the brighter contrast. With a slow-cooling rate, the interfacial stress can be released by a large area, continuous flake-substrate delamination, while with a fast-cooling rate, the interfacial stress tends to be released through local lattice reconstructions. Fast cooling exerts larger cooling stress due to less strain relaxation, providing larger tensile stress on the 1L-ReS2. As a result, the fast-cooling ReS2 flakes have more needle-like patterns.

Fig. 3: DFM topography and phase images of CVD-grown 2D ReS2 with different cooling rates.
figure 3

a–c Polarized OM images of 1L-ReS2/mica synthesized with the slow-cooling rate (5 °C min−1), normal slow-cooling rate (25 °C min−1), and fast-cooling rate (120 °C min−1), respectively. d–f DFM topography image and phase image corresponding to samples in a–c, respectively. g–i Line profiles corresponding to dash black lines in d–f.

Full size image

The residual stress/strain is distinctly different in the original lattice (delaminated) and lattice reconstructed domains. More strain is released in the lattice reconstructed areas (Fig. 2), leading to lowered remaining stress in those areas. According to the DFM topography results, the magnitude of the partial delaminations in lattice reconstructed domains is within 0.1–0.2 nm. With delaminations, the lattice mismatch strains between ReS2 and substrate upon cooling are released. According to the Poisson ratio effect (elasticity of membranes), if the tensile strain in the membrane is relaxed, the thickness of the membrane will increase, in agreement with our DFM results as well. On the other hand, it is intrinsic behavior for the different optical responses under polarized light along with the different lattice directions (or domains) in 2D ReS227. However, in our experiments, the contrast of ARPR spectroscopy and DFM topography results between different domains should be attributed to the contrasted residual strain levels in the pristine and reconstructed domains.

The strain-originated domain structure can also explain the absence of domain patterns in the mechanical exfoliated ReS2 flakes. The mechanical exfoliated flakes mainly experienced out-of-plane stressing instead of in-plane stress which might induce domain structures. Except for the out-of-plane bending, no apparent in-plane straining that is required for mechanical twinning is applied during the mechanical exfoliation process42. In CVD-grown flakes, owing to the easier relief of interfacial stress in smaller flakes and larger residual stress remained in larger flakes, the smaller 1L-ReS2 flakes usually possess remarkably less domain structures (Fig. 4a–f). It is also found enhanced/increased domain structures in 1L-ReS2 grown on SiO2/Si substrate, compared with fluorophlogopite mica and c-face sapphire. It is attributed to the larger thermal expansion coefficient (TEC) misfits of SiO2/Si with 2D anisotropic materials (Fig. 4g–o and Supplementary Table 1). The substrates with lower TEC such as Si/SiO2 will shrink much less than 1L-ReS2 during cooling, hence induce a larger traction force. The CVD-grown ReS2 samples after transfer onto another substrate (Supplementary Fig. 1) kept the original patterns after synthesis due to no additional loading is applied in the processing. For the multilayer specimens, the cooling down strain can be actually transferred by interlayer interactions (signature of T′ phases of TMD materials)43, inducing similar lattice switching behavior throughout all the thicknesses.

Fig. 4: Size dependence and substrate effects.
figure 4

a, b The DFM topography image and phase image of 20 µm 1L-ReS2 grown on fluorophlogopite mica. c, d The DFM topography image and phase image of 10 µm 1L-ReS2 grown on fluorophlogopite mica. e, f The DFM topography image and phase image of 5 µm 1L-ReS2 grown on fluorophlogopite mica. g–i, j–l, m–o The optical micrographs of CVD-grown ReS2 on 300 nm SiO2/Si, c-face sapphire, and fluorophlogopite mica substrates, respectively.

Full size image

The sub-domains boundaries trigger by the above lattice reconstructions have been fully corroborated by our high-resolution scanning transition electron microscopy (STEM) observations (Fig. 5a–c and Supplementary Fig. 6), which should be nucleated from the free edges (lowest strain energy cost at the edges). In the case of CVD cooling down the process for 2D ReS2 in our experiments, the biaxial thermal expansion difference between ReS2 and underlying substrates (mica or sapphire) created a tensile strain field in ReS2. There are no clear boundary conditions for strain/stress, the ReS2 flakes and substrates are engaged by the vdW interactions (can be rationalized as static frictions) at the interface. In contrast to the out-of-plane buckling under compressive cooling down strains in 2D WS244, the interactions between ReS2 and substrates here can create the homogeneous in-plane tensile strain in 2D ReS2, while the relative sliding and delamination between 2D flakes and the substrates prefer to start at the free edges (Fig. 5d, e). Assuming the frictional force (between ReS2 and substrate) is constant (maintained at maximum) in final states near edges at room temperature, the tensile stress/strain can be assigned according to the location in the 2D flakes (Fig. 5f, g). Apparently, the normal stress pointing to the edges will decrease from the corners to the interiors along edges, causing the shear strain in the “wing” like structures. Therefore, the energy favorable twinning domains will be triggered from the corners, sweep over half of the edges, and be ceased at the middle points of edges, as we observed above. The delaminated half (brighter half in the DFM topography images, e.g., Fig. 1d–f) thus have less or even no sub-domain structures due to the relief of interfacial stress upon this first-step delamination, while the undelaminated half (darker half in the DFM topography images) will undergo further transformations by the tensile stress starting from the edges, forming the needle-like sub-domains in the darker half.

Fig. 5: The STEM images and illustration of strain field in ReS2.
figure 5

a–c The STEM annular dark field (ADF) images showing the typical twinning domain boundary structures stemming from free edges, the diamond chain directions (b direction in Fig. 6) are highlighted, scale bars =1 nm. d The tensile tractions on ReS2 flake exerted by the engaged substrate. e The sketch map of the tensile strain level, decreasing from the center to flake edges. f The mechanical schematic of tensile strain resulted interfacial sliding and traction forces in equilibrium. g The diagram illustration traction and strain level associated with the location in the sample flakes.

Full size image

The lattice reconstructed domains thus can have stark differences in residual stress, especially between sample and substrates. Compared to the original lattice domains (delaminated sub-domains), the interfacial strains have been largely released during lattice reconstructions in reconstructed domains. The contrasts between original and reconstructed domains seen by the DFM topography images (Fig. 1e) and the polarized optical characterizations (Fig. 2b–i) can be attributed to the strain differences between reconstructed and pristine domains. Particularly, the small shear angle changes in lattice directions, for pristine and reconstructed domains, can also be clearly visualized on free edges in the DFM/optical images (Fig. 1a, c, d and 3). The tensile traction exerted on the monolayer ReS2 samples will cause the stripe patterns along certain crystal directions (Figs. 1e and 4). Since all of the twin boundaries shown in Fig. 6 have very low lattice mismatches thus low formation energies, in real samples we can found quite complicated domain structures consisting of all the possible domain boundaries, crossing with angles close to 30°, 60°, 90°, 120°, and 150° (Supplementary Fig. 7).

Fig. 6: The structural and strain analysis of twin structures by lattice reconstructions in 1L-ReS2.
figure 6

a The original (pristine) lattice relaxed by DFT calculations. Specific vectors are defined for low-index crystal orientations (<100> and <110> directions), and only Re atoms shown. b The lattice in mirror symmetry to a. Lattice in b can be considered as after reconstruction from a. c–e, i–k Scheme of the twinning domain boundaries (zigzag lines) along different low-index orientations. Lattice orientations for two opposite sides of twin boundaries are shown by arrows. f–h, l–n The shear angle of labeled crystal directions and the normal strain (only f–h, normal strain for l–n is zero) for reconstructed lattices compared to pristine lattices, corresponding to the six types of twin boundaries above (c–e, i–k), respectively. o, p The domain types resulted from corresponding lattice reconstructions. Panel o corresponds to c–e type twin boundaries, while panel p corresponds to i–k type twin boundaries.

Full size image

The structural and strain analysis of twin structures by lattice reconstructions in 1L-ReS2

2D ReS2 has a monoclinic crystal structure or called T′ (tetrahedral) phases39,45. This structure is flexible to switch either two of the base vectors (a,b,i) under ultra-low straining (see Fig. 6a, b, and Supplementary Fig. 8), the 1L-ReS2 structures are relaxed by density functional theory (DFT) calculations, see “Methods” section. We have listed all the possible normal strains and shear strains that can result in the lattice switching (viz. lattice reconstruction) in monolayer ReS2 (Fig. 6c–n). For the three types of twin boundaries (Fig. 6c, d, e), the twin boundary directions are always in 0° or 60° with respect to the zigzag edges of 2D ReS2, while for the other three types of twin boundaries (Fig. 6i, j, k), the twin boundary directions are in 30° or 90° with respect to the zigzag edges of 2D ReS2. Therefore, we can readily distinguish these two groups of twin boundaries from the DFM or polarized OM images. It should be noted here that the strain condition needs to be comprehensively understood with the domain structures resulted from lattice reconstructions, and the strain effect for these lattice reconstructions are not relevant to the exact atomic structures of the domain boundaries, but only determined by the original (pristine) and the reconstructed domains. In principle, there is no strain along all the twinning domain boundaries. However, in other directions, the lattice reconstructions can accommodate the in-plane normal strain (either compressive or tensile) from −1.5% to 2.5%, and the in-plane shear strain (in terms of shear angle for certain directions) from −1.6° to 3.4° (Fig. 6c–n), depending on the orientation of twin boundaries (along a,b,i,u,v,w, respectively, see Fig. 6a for the definition).

Apparently, the domain boundaries prefer to be twinning boundaries for the lowest energy cost (least lattice mismatch and zero strain along twin boundary directions). The remarkable low shear or normal strain (shear angle <1–2°) that absorbed by twinning are associated with the lattice reconstruction in such anisotropic 2D materials. The parallel needle-like or stripe-like domain structures well resemble the famous martensite phases46 widely existed, however, the energy required for twinning here are much lower than the normal mechanical twinning. Therefore, such lattice reconstruction can act as an efficient deformation mechanism for low straining level in 2D ReS2. Classified by boundary angles with respective to the ReS2 edges, the triangular domain structures (twin boundary in 90° or 30° with edges) and the parallel stripe domains (twin boundary in 60° with edges) can be correlated with the deformation under shear and normal stress in samples, respectively (Fig. 6o, p). In addition, it should be noted that if the sulfur (S) atoms are considered, the lattice symmetry normal to the basal plane needs to be counted. That is, the S atoms cannot penetrate the basal plane during lattice reconstructions, so only the cases shown in Fig. 6c–e are entirely twin boundaries (for both Re and S atoms), whereas the cases in Fig. 6i–k are twin boundaries for Re atoms, but inverse twin boundaries for S atoms.

Next, opposite to the tensile strain discussed above, we will focus on the effects of compressive stress on the 2D anisotropic materials. The biaxial compressive strain in 2D materials can be generated by flexible substrates in the previous works47. Albeit the wrinkle patterns can be frequently seen in 2D materials strained by the underlying flexible substrates48,49, mechanical approach is less controllable, particularly for biaxial straining. Here we applied ultraviolet (UV) exposure with moisture condition on the 2D ReS2 samples (see “Methods” section for details). Unlike the previous graphene or isotropic TMD materials50,51, the regular wrinkle patterns emerged in 2D ReS2. As seen from the DFM characterization results, the wrinkles preferentially follow the low-index directions (Fig. 7 and Supplementary Figs. 9, 10). The wavelengths, wrinkle heights for these three main directions are maintained almost identical throughout all the sub-domains in the flake (originated from CVD cooling) (Fig. 7e, f). Therefore, the wrinkle patterns also exhibit the domain patterns following the crystals. Apart from the preferences in crystal orientations, the wrinkles are prone to be formed along the domain boundaries. More wrinkle patterns generated can be found in Supplementary Fig. 10.

Fig. 7: The results of DFM characterizations and wrinkling behavior of 1L-ReS2 as grown on fluorophlogopite mica substrate after 180 s UV treatment.
figure 7

a–d The DFM topography and phase images for pristine 1L-ReS2. e, f The DFM images for 180 s UV treated ReS2 flake in a and c, respectively. The white dashed lines with arrows indicate the different directional wrinkles and the sub-domain boundaries are marked by purple dashed lines.

Full size image

The compressive strain above is supplied by the photochemistry relevant to the surface of ReS2 (see “Methods” section). The oxygen and hydroxyl radicals introduced by UV treatment are able to anchor in the lattice space lead to the compressive strain in the lattice. Supplementary Fig. 11a–c shows the TEM characterization result of the spontaneous 2D wrinkling in monolayer ReS2 under the biaxial compressive field. The wrinkles formation during UV treatment tends to follow the energy favorable directions—along basis vectors a or b. As shown in Supplementary Fig. 11d, the expansion of lattices after UV oxidation is confirmed by our DFT simulations. The basal plane is expanded during UV treatment meanwhile the ReS2 are constrained by the underlying substrates, subsequently, the wrinkles can be developed to release the stress. The atomic structures of 1L-ReS2 can be slightly distorted with the exotic covalently-bonded surface oxygen atoms41. The ReS2 fold (Supplementary Fig. 11e) is also in part owing to the stacking of two counter layers after folding (the stable wrinkles can be reckoned as vertical folds)52,53, along these directions has the lowest interlayer energies. It should also be noted that due to the monoclinic structure of 1L-ReS2, the folded two layers (in mirror symmetry) cannot match each other (rotate by 1–2 degrees) with the original lattice. Therefore, to minimize the stacking energy of the wrinkles, lattice switching can take place and accommodate the strains (Supplementary Fig. 11f).

The wrinkles along the grain boundaries (by merging/stitching of grains during growth from different nuclei) (Fig. 7e, f) are also clearly observed. The wrinkle structures close to the edges are related to the special strain distribution along the edges (almost zero strain parallel to edges), hence the remaining compressive strain perpendicular to edges will generate the perfect periodic one-dimensional wrinkle patterns. Close to the edges, there are always less interactions from the substrate effects, rendering the wavelength/period of the wrinkles also become larger at edges (Supplementary Fig. 10).

According to the above experiments and explicit analysis, it has been clarified that the strain effects play essential roles in the formation of martensite-like structures and the twinning domain boundaries in anisotropic 2D materials such as ReS2, and ReSe2. These domain structures can conversely have a significant impact on the mechanical behavior as well as other physical properties. The rich atomic structural reconstructions under strain loading, and the associated strong anisotropy in physical properties (electrical, electronic, optical, etc.), could open great opportunities for future strain engineering on these anisotropic 2D materials.

Methods

Synthesis of ReS2 on fluorophlogopite mica, c-face sapphire and 300 nm SiO2/Si, MoS2 on 300 nm SiO2/Si substrates

1L-ReS2 and MoS2 flakes are synthesized in a two-splitting heating center tubular furnace. Firstly, 2 mg ammonium perrhenate (NH4ReO4) (Aldrich, 99.999%) powder for ReS2 growth, sodium molybdate dihydrate (Na2MoO4·2H2O) (Aldrich, 99%) for MoS2 growth is placed in a quartz boat and covered by a piece of 1 cm * 1 cm fluorophlogopite mica (KMg3AlSi3O10F2), c-face sapphire or 300 nm SiO2/Si substrate then located on the downstream heating center. Next, 100 mg sulfur (Aldrich, 99.998%) plates for ReS2 and MoS2 growth are placed in a separated quartz boat located on the upstream heating center.

As the downstream heating center ramped up to 850 and 800 °C, for ReS2 and MoS2 growth, respectively. Meanwhile, the upstream heating center climbed to 200 °C. The 80 sccm Argon carrier gas is introduced during synthesis. After maintaining the target temperature for 10 min, the furnace is cooled down naturally.

Transfer of ReS2 sample on SiO2/Si, TEM grid

The as-grown ReS2 was spin-coated with polymethyl methacrylate (PMMA) (A4) to form PMMA/ReS2/substrate structure. Next, the PMMA/ReS2/substrate is floated on the 75 °C ultrapure water for one hour to detach PMMA/ReS2 from the substrate. Following, a 300 nm SiO2/Si substrate or QuantifoilTM TEM grid is applied to scoop out the PMMA/ReS2 film. Subsequently, the PMMA/ReS2 on the target substrate was dried under ambient temperature to increase the adhesion between ReS2 and the target substrate. Finally, the acetone or acetone vapor is introduced to remove the PMMA layer on 300 nm SiO2/Si substrate or on the TEM grid, respectively.

Prepare of ReS2 on SiO2/Si from a bulk sample

With the assistance of the semiconductor transfer tape (USI, Blue Adhesive Plastic Film), bulk ReS2 (2D Semiconductors Inc., USA) was exfoliated into pieces and attached to a 300 nm SiO2/Si substrate.

UV treatment method

1L-ReS2 on the substrate is placed into a chamber fitted out a mercury lamp (LH-arc, Lichtzen Co. Ltd, Korea) with ~90% of emitted light at a wavelength of 254 nm and the minority of light at a wavelength of 185 nm (20 mW cm−2). The chamber is connected with two injection pipes and one output valve. One injection pipe is for a humidifier to introduce moisture, while another one is for N2 gas to extrude the humid and the output valve is used to balance the pressure at ambient pressure. The humid level was monitored using a hygro-thermometer (accuracy ± 3%). The 1L-ReS2 is treated with UV light for 180 s. The radicals were generated by UV light treated moisture air as the following reactions:

$${{{{\rm{O}}}}}_{2}\to {{{{\rm{O}}}}}_{3},{{{{\rm{O}}}}}_{3}+{{{{\rm{H}}}}}_{2}{{{\rm{O}}}}\to {{{{\rm{H}}}}}_{2}{{{{\rm{O}}}}}_{2}+{{{{\rm{O}}}}}_{2},2{{{{\rm{O}}}}}_{3}+{{{{\rm{H}}}}}_{2}{{{{\rm{O}}}}}_{2}\to 2{{{{\rm{OH}}}}}^{\ast }+3{{{{\rm{O}}}}}_{2},{{{{\rm{H}}}}}_{2}{{{\rm{O}}}}\to {{{{\rm{OH}}}}}^{\ast }+{{{{\rm{H}}}}}^{\ast }.$$

Angle-resolved polarized Raman (ARPR) measurement

The ARPR measurement is performed using a commercial inVia confocal Raman microscope (Renishaw, UK) with a ×50/0.75 N.A. objective (LEICA, German) with a spatial resolution ~1 µm. The ARPR of ReS2 and MoS2 are measured at excitation wavelengths of 785 nm (~1.6 mW power) and 514 nm laser (~0.54 mW power) with 1200 l mm−1 grating and 1800 l mm−1 grating with a ×50/0.75 N.A. objective (LEICA, German), respectively. The laser power is calibrated using standard photodiode power sensor S121C (Thorlabs, USA). The ARPR measurement setup is equipped with a rotatable Polarizer I, one half-wave plate, and a linear Polarizer II, the setup shown in Supplementary Fig. 4. The ARPR spectra are recorded every 10° with the incident laser being rotated by Polarizer I from 0° to 360° while the sample is fixed. As analyzer, the half-wave plate and the linear Polarizer II are applied to collect the scattered light. The ARPR spectra were fitted using Gaussian contributions to extract the peak intensity value.

DFM measurement

The topography and phase images are recorded using an AFM5300E system (HITACHI, Japan) in cyclic contact mode. The topography image and phase image are recorded through detection of the oscillation evolution of the cantilever. Initially, the cantilever oscillation is driven by the input signal. During the scanning, the force between the probe and the sample surface is maintained to be constant then the cantilever oscillation state changes. On the one hand, the topography images are generated by the amplitude evolution of the cantilever oscillation as shown in Supplementary Fig. 12a. On the other hand, the phase shift contrast is attributed to the energy adsorption of the sample surface, such as the delaminated area will have the less adsorptive energy, which results in a smaller phase shift (Supplementary Fig. 12b). The n-type silicon tip NSG30 (Tipsnano, Estonia) with Au coating on the reflective side is used for the measurement. The tip curvature radius is ~35 nm with typical resonant frequency and force constant at 320 kHz and 40 N m−1, respectively.

DFT calculations

Structure relaxations and energies of ReS2 are calculated by using density functional theory as implemented in the Vienna ab initio simulation package (VASP)54,55 within the projector augmented wave (PAW)56. The Perdew, Burke, and Ernzernhof (PBE) exchange-correlation functional57 of the generalized gradient approximation (GGA)58 is used to describe the electron interactions. A plane-wave cutoff energy of 450 eV is adopted for all the calculations. The vacuum space in z direction is set to be more than 15 Å to prevent the interaction between layers. The criteria for convergence in energy is 10−5 eV. Structure relaxations and lattice constant are obtained by optimizing all atomic positions until the Hellmann-Feynman forces are less than 0.02 eV Å−1. The Brillouin zone is sampled with 8 × 8 × 1 Γ centered k points for structural optimizations.