Designing bioinspired brick-and-mortar composites using machine learning and statistical learning

Abstract

The brick-and-mortar structure inspired by nature, such as in nacre, is considered one of the most optimal designs for structural composites. Given the large number of design possibilities, extensive computational work is required to guide their manufacturing. Here, we propose a computational framework that combines statistical analysis and machine learning with finite element analysis to establish structure–property design strategies for brick-and-mortar composites. Approximately 20,000 models with different geometrical designs were categorized into good and bad based on their failure modes, with statistical analysis of the results used to find the importance of each feature. Aspect ratio of the bricks and horizontal mortar thickness were identified as the main influencing features. A decision tree machine learning model was then established to draw the boundaries of good design space. This approach might be used for the design of brick-and-mortar composites with improved mechanical properties.

Introduction

Data-driven methods such as machine learning (ML) and statistical analysis (SA) are efficient toolsets for extracting process–structure–property relation or for design–synthesis–characterization of materials^{1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18}. ML and SA are able to address large and complex tasks by focusing on the most relevant information in an overwhelming quantity of data while providing similar or better accuracy to the finite element analysis (FEA) and experiment^19,20,21,22.

In particular, ML and SA have been used for design analysis of various composites and structural materials. Alakent and Soyer-Uzun implemented statistical learning methods to develop design guidelines for biocomposites with high tensile strengths²³. Chen and Gu used an integrated approach combining finite element method, molecular dynamics, and ML to investigate the effect of constituent materials (assumed to be perfectly brittle) on the mechanical behavior of composites²⁴. Gu et al. used a perceptron and convolutional neural network (machine/deep learning model) to demonstrate their capacity to accurately and efficiently predict the toughness and strength of a two-dimensional (2D) composite²⁵. The results showed that ML accurately predicted the performances of composite geometries relative to each other. The optimum structures of the composite in terms of strength and toughness were obtained. Qi et al. used an artificial neural network to predict the unconfined compressive strength of cemented paste backfill²⁶. Tiryaki and Aydin employed ML models to predict the compression strength of heat-treated woods²⁷. Deep learning approaches were used for mining structure–property linkages in high contrast composites from simulation datasets, and to establish structure–property localization linkages for elastic deformation of three-dimensional high contrast composites^16,18.

 Yang et al. developed deep learning models to capture nonlinear mapping between three-dimensional material microstructure and its macroscale (effective) stiffness¹⁶. Due to the lack of a suitable experimental data set, they assumed that the ground truth could be captured by the results of micromechanical finite element models. They employed a multilayer perceptron neural network (ML model) and convolutional neural network (ML/deep model). The results showed that the proposed convolutional neural network outperforms the sophisticated physics-based classic approaches by as much as 54% in terms of testing the mean absolute stiffness error. However, the deep learning approach did not perform very well for some mid-range values of effective stiffness.

This manuscript presents a ML statistical learning approach for the analysis and design of brick-and-mortar composite architecture with a large data set (>20,000 samples). The structure of the “brick-and-mortar” composite is shown in Fig. 1. This architecture is inspired by natural materials, and there have been many studies in the literature aiming at manufacturing such composites^{28,29,30,31,32}. Natural materials such as nacreous part of sea shells have developed structural composites, using a set of rather ordinary constituents, which exhibit extraordinary mechanical properties. For example, sea shells convert a brittle ceramic material (aragonite calcium carbonate) to a super-tough material (nacre) by incorporation of ~5% polymer, in a layered brick-and-mortar microstructure. More specifically, the fracture toughness of aragonite is ~0.25 MPa m^1/2, while the toughness of nacre is ~10 MPa m^1/2, a 40-fold increase in toughness, and a factor of nearly 2000 in terms of energy^28,33. If we are able to improve the fracture toughness of synthetic composites by 40-folds through bioinspired design principles (e.g., brick-and-mortar microstructure), we will obtain composite materials that have the strength, stiffness, and low weight of ceramics, while their fracture toughness and work-to-failure matches or surpasses those of metals and alloys.

Fig. 1: The brick and mortar architecture and the representative volume element.

a A brick‐and‐mortar composite microstructure. Bricks are arranged in a staggered pattern, which are perfectly bonded with the mortar. The mortar (soft and ductile) and the bricks (hard and brittle) are represented by blue and gray, respectively. b The selected RVE (representative volume element) with the geometrical features. The mortar is divided into two sections: the vertical and horizontal sections, which for clarity are colored red and blue, respectively. The definition of each symbol is given in Table 2. VI and HI are the vertical and horizontal interfaces, respectively. w and h are the brick length and height, respectively. t₁ and t₂ are mortar vertical and horizontal thickness, respectively, and s is the shift in stagger arrangement.

In this work, the mortar and bricks were assumed to be metal and ceramic, respectively. Metal–ceramic composites have been identified as the most promising type for brick-and-mortar architecture. For the brick-and-mortar composite architecture, there are several geometrical design parameters, including the mortar volume fraction, the aspect ratio of the bricks, mortar thickness, and shift in stagger arrangement of the bricks, among others. Additionally, materials properties of the brick and mortar should be also added to this list. Such a large design space cannot be fully examined by experimental work since manufacturing processes for such composites are often costly^28,29.

In Fig. 1, the bricks and mortar regions are respectively colored gray and blue. The mortar is further split into vertical (VI) and horizontal (HI) sections (red and blue regions in Fig. 1b, respectively). The smallest informative repeating section was selected as the representative volume element (RVE), assuming that the global behavior of the brick-and-mortar structure is the same as that of the RVE (Fig. 1)³⁴. The RVE consists of bricks, and vertical (VI) and horizontal (HI) mortars regions^35,36. The RVE contains two bricks that are separated by HI vertically and shifted by s horizontally. For transverse loading, the boundary conditions consist of symmetric conditions along the left and bottom edges of the RVE (Fig. 2). In addition, the top and right edges were constrained to have equal displacements in the perpendicular direction to satisfy periodic boundary conditions. Therefore, it is possible to apply uniform stress to the RVE by applying a point force to one point on the right edge. The imposed periodic boundary conditions on the RVE cannot handle the application of other loading types, for example, shear. Moreover, the RVE can only predict the strain/stress distribution within the bulk composite and it does not consider the edge effect.

Fig. 2: RVE periodic boundary conditions (BCs).

The applied periodic boundary conditions restrict the top and right edges of the RVE to remain parallel to their initial positions by adding two constraints to the nodes on the right and top sides of the RVE to have equal displacements in the x and y directions, respectively. Uniform tensile stress with the magnitude of one is applied to the right edge of RVE.

In this work, the strength is evaluated using the elastic deformation analysis to predict the stress required to trigger various failure modes. Based on the theoretical failure modes, the designs are split into two classes, that is, “good” and “bad.” For the brick-and-mortar structure, the ideal failure mode is the failure of the vertical mortar, followed by failure of the horizontal mortar, and subsequent pull-out of the bricks. Such a failure mode results in the highest fracture toughens. In this work, we assigned good design to the cases that the VI fails first. In the good class, the composite can still carry the load by horizontal mortar and bricks after VI failure^{37,38,39,40,41}. Therefore, the other two (HI failure and brick failure) were considered as a bad design. Using the data set, ML models were trained to capture the relationships between the features and classes (classification). Furthermore, to illustrate the potential of the ML approach beyond classification, a quantitative regression ML model was also developed to estimate the strength. More specifically, the proposed regression model was employed to capture the nonlinear mapping between the composite microstructure and its strength.

The presented model can predict the strength of high contrast elastic composites with a wide range of microstructures while exhibiting high accuracy and very low computational cost for new evaluations. It was found that the thickness of vertical to horizontal mortar ratio (TR) and the aspect ratio of the brick (AR) are the main influencing features defining the design class while mortar volume fraction (v_m) and shifting distance of the bricks (s) are not significantly different for each class. Moreover, these results emphasize the importance of simultaneously controlling TR and v_m. The high and low values of TR and v_m, respectively, assure the high strength, while low AR can be used for good design.

Results

Data generation

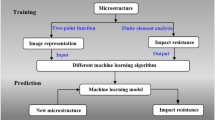
The data generation procedure and ML model development are shown in Fig. 3. The data set was generated by MATLAB and ABAQUS. Mechanical strengths obtained from FEA were considered as the ground truth and held the correct class. The failure of the VI, HI, or bricks and their combination are the main failure modes of a brick-and-mortar composite (Fig. 1b). Each failure mode results in different strengths and toughness levels. Theoretical models predict that the most desirable failure mode is the VI failure first, followed by HI failure³⁷. Following VI and HI failure, the bricks can pull-out, which is preferred to brick failure. The brick failure will result in catastrophic failure. Therefore, in this work, we categorized failure modes with VI-failure-first as “good.” Classifying the data into the good and bad design was done by comparing the maximum stress in VI, HI, and bricks with their corresponding strength, given that the system is considered to behave elastically. Finally, all geometries in the data set were categorized into “good” labeled as “1” and “bad” labeled as “0” classes²⁵. Higher stress in VI would result in lower composite strength in good designs. Hence, the strength in the good design was defined by reciprocal of the maximum stress in VI. The generated data set (D) contains the geometrical features, the classes, and the strength of ~20,000 samples. D was then randomly partitioned into three non-intersecting sets: training data set (D_training) = 70% of D, validation data set (D_v) = 10% of D, and test data set (D_test) = 20% of D for ML calculation.

Fig. 3: Data generation and ML model development procedure.

The data set was generated by MATLAB⁵³ and ABAQUS⁵². Mechanical strengths obtained from FEA were considered as the ground truth and held the correct class. The classification to good and bad classes was done through the decision tree with its leaves representing different features conditions. A support vector regression was used for strength prediction.

Machine learning model

Figure 4 shows the depth effect on the decision tree performance. The decision tree construction strongly depends on the number of branches (depth)^42,43. To accurately select the depth, decision trees with different depths from 1 to 11 were evaluated over D_v. We used the area under the receiver operating characteristics curve (AUC, the area under the curve) as the evaluation metric. The results showed that the highest AUC value is 0.95, and it belongs to the decision tree with depth 6. Therefore, the decision tree with depth 6 was selected as the optimum case with the least bias and variance. The decision tree can distinguish a 2D brick-and-mortar structure as either a “good” or a “bad” design. For geometries labeled as “good” designs in the data set, their performances can be compared in the terms of strength. A support vector regression (SVR) with the radial basis function (RBF) kernel was employed to predict strength values.

Fig. 4: The depth effect on the decision tree performance.

a The AUC (area under the curve) vs. the depth for the decision tree, and the b MSE (mean squared error) as a function of γ (hyperparameter) for SVR with the radial basis function (RBF) kernel over D_v (validation data set). The dashed lines show the selected value for each hyperparameter.

RBF is one of the most widely used kernel functions because of its ability to generalize nonlinear functions and efficiently manage large datasets. SVR specifies the epsilon-tube within which no penalty is associated with the training loss function with points predicted within a distance epsilon from the actual value. Scikit-learn implementation of SVR is a wrapper around LIBSVM⁴⁴ that uses the decomposition method as the optimizer⁴⁵. The MSE was used to measure the difference between the strength predicted by SVR and the actual value from the FEA results (Fig. 4b). The MSE equation is expressed as:

$${\mathrm{MSE}} = \frac{1}{n}\mathop {\sum}\limits_{i = 1}^n {(y_{\mathrm{prediction}} - y_{\mathrm{true}})},$$

(1)

in which y_prediction and y_true are the predicted strength and the actual strength for geometry i in D_v, respectively. γ is an important hyperparameter for SVR⁴⁶. The MSE vs. γ over D_v is shown in Fig. 4b. γ ~0.15 shows the least MSE and was selected for this problem. The obtained hyper-parameters for ML models are given in Table 1.

Table 1 The hyper-parameters for each ML prediction model.

Feature selection

The presented method was used to generate a data set containing a large amount of information. The selection of relevant features and the elimination of irrelevant ones is one of the central problems in SA and ML⁴⁷. By focusing on only a small subset of features, an ML algorithm significantly reduces the number of hypotheses under consideration and can quickly search for better designs from a very large number of possible composite designs for further evaluation. The good geometries may have simple geometric patterns, which are easier to be recognized. Therefore, we first tried to find the relevant features that determine whether a design is good or bad.

To select the relevant features, an SA of the features was carried out. The distribution of features, that is, AR, TR, s, and v_m in good and bad classes in the D_training are displayed in Fig. 5. In the box plot, the black line is the median. The bottom to top of each box show 25–75% (interquartile) range. The results reveal that medians and the range of AR and TR for the good and bad designs are fully separable. The figure shows more than 75% of the data in good class has the TR and AR below ~1.3 and ~18, respectively.

Fig. 5: The distribution of features in good and bad classes in training data set (D_training).

The box plot for different features’ distribution in the good [1] and bad [0] designs in D_training: a AR, b TR, c s, and d v_m. The segments inside each box show the median and the whiskers above and below the box show the minimum and maximum. The boxes contain at least 75% of the training samples. Filled circles in a, b display surprisingly high maxima or surprisingly low minima. All the features’ distributions are almost symmetric expect the TR in good design that shows skewed distribution. TR (horizontal mortar ratio), AR (the aspect ratio of the brick), v_m mortar volume fraction, and s (shifting distance of the bricks).

No visible correlation between s and v_m for the classes is observed since they are approximately balanced around the mean values for both classes. Therefore, TR and AR were the selected features for the classification problem. It is worthy to note that considering only two features, that is, AR and TR as the input for classification problem drops the computational cost while maintaining the performance. The maximum AUC of decision tree classifier on all features (with depth 10) was calculated to be just ~3% higher than the decision tree on just two features, that is, AR and TR (with depth 6).

Classification

Based on the results of SA, AR and TR were selected to train a decision tree classification model. The construction of the decision tree strongly depends on the number of branches (depth). A complex tree with a large depth may be overfit to the data, while a simple tree with small depth may be underfit to the data. To carefully select how training parameters in the decision tree affect the prediction, the number of branches was systematically varied in the training process. The good and bad classes produced in the pre-processing step were considered as the ground truth and held the correct classes. The AUC of the decision tree models over D_v is shown in Fig. 4a. The AUC of the decision tree increases to 0.95 by increasing the depth to 6. No further AUC improvement is observed afterward. Therefore, 6 is the optimum value for depth that provides the highest performance and simplicity. The selected decision tree showed the same values of AUC over D_test. D_training in AR-TR space (Fig. 6a) and partitioned AR-TR space (Fig. 6b) is depicted in Fig. 6. Good design in D_training dominates a larger portion of the space. Seventy-five percent of the D_training is good design, and only 25% is bad design. The developed decision tree was used to partition the AR-TR space. Figure 6b shows the boundaries created by the decision tree for the good and bad classes. Eighty-three percent of the AR-TR space is colored in orange (good design).

Fig. 6: Boundaries of the good and bad design in design space and the stress distribution in selected points.

a Scatterplot of good and bad designs in TR-AR design space for D_training. The response is color coded: the orange cross and blue circle represent points in the good and bad classes, respectively. b The partitioned space by the decision tree. Orange and blue correspond to good and bad classes, respectively. c The von Mises stress distribution obtained from FEA for selected points shown in a. The stress contours are von Misses stress, and the figures are undeformed geometry of the RVE. The stress magnitude is normalized with respect to the applied load. The selected points illustrate the different failure possibilities: the black triangle represents a sample in the good class (VI fails first). The black circle and square are examples of bad designs with HI and brick failure, respectively. The red color shows the region with the highest stress value. All the geometries in c have the same value of s = 0.2 and v_m = 0.5 while they present different failure modes. The heights of RVE obtained from Eq. 1 and Eq. 2 are 0.43, 0.1, and 0.15 for the points shown by the triangle, circle, and square point in a, respectively. The stars in c show the location of the failure initiation. Failure is considered as the onset of yielding in the mortar and fracture of the ceramics. TR (horizontal mortar ratio), AR (the aspect ratio of the brick), v_m mortar volume fraction, and s (shifting distance of the bricks).

Figure 6c shows stress distribution for the samples in D_training (selected points in Fig. 6a) with different failure modes. Regions of the bricks just above and below the VI have the highest stress values for all the cases (Fig. 6c). Therefore, they are susceptible regions for brick failure. As shown in the pie chart in Fig. 7, 5% and 20% of the geometries in the D_training have HI and brick failure as the failure mode, respectively. Figure 7 displays the probable location of failure for each failure mode, that is, VI, HI, or brick failure. As it was expected, the failure probability of the brick above or below of VI is ~94% due to higher stress concentration (Fig. 6c). Eighty-five percent of HI failures happen near brick corners due to stress concentration.

Fig. 7: The probable location of failure for each failure mode.

a A pie chart that shows the percentage of different failure modes in the D_training. Failure position for different failure modes with >1% probability: b HI, c VI, and d brick failure. HI (horizontal interface) and VI (vertical interface).

Regression

In addition to being able to determine the strength value, a regression model can also be implemented to rank the designs based on their strength. Figure 8 shows the ranking comparison predicted using the SVR model and the actual strength ranking in the D_training and D_test. It can be argued that the regression model predicts ranking in the D_training with high accuracy for strength since the majority of the points lie very close to the line y = x. Additionally, as can be seen in Fig. 8, although the SVR model does not observe the FE strength or FE ranking information, the results are also impressive when predicting the ranks of geometries in D_test. The decision tree and regression model are very useful when using ML as a filter to quickly search for better designs with high accuracy from a very large number of possible composite designs for further evaluation in a short period.

Fig. 8: Ranking comparisons for ML regression and the FEA model.

a, b show the comparisons between the rankings obtained from the FEA and the linear model over D_training and D_test, respectively. The red dashed lines represent y = x. The size of D_training and D_test are 14,566 and 6937, respectively.

Geometrical pattern

The previous section has shown that our ML model can accurately categorize geometries and rank geometries relative to each other. One question is whether the ML models can actually capture the physics and mechanics of this composite design problem based on the patterns they have earned. Figure 9 shows the frequency distribution of the features and strength over D_test. The results demonstrate that, on average, the ML models can predict the geometries that have high-strength, nearly as well as the FEA approach, without ever solving finite element equations. High similarities between the geometrical patterns of ML and FEA are observed. It is interesting to note that the majority of geometries provide a low strength while only a small fraction of them has high strength (Fig. 9). The average strength of D_test is ~0.74, while the top 100 samples have a strength of ~0.99.

Fig. 9: The frequency distribution of the features and strength over D_test.

a Frequency histogram of strength for geometries obtained from the FEA and those obtained from ML models. The results are normalized w.r.t. the maximum strength in D_test. The frequency histogram of geometrical features in the top 100 models in D_test predicted by ML and FEA: b AR, c TR, d s, and e v_m. TR (horizontal mortar ratio), AR (the aspect ratio of the brick), v_m mortar volume fraction, and s (shifting distance of the bricks).

The feature frequency histogram for the top 100 geometries is shown in Fig. 9b–e. Considering the top geometries for both properties obtained from the FEA and ML, there are high similarities in frequency distributions. The optimal combination of mortar and brick geometries that maximizes strength would be the designs with TR above ~1.6, v_m below ~0.3, and AR between 10 and 20. Without considering mechanics knowledge, without even knowing the geometry, the ML models find the patterns that lead to high strength. As can be seen from Fig. 9c, d, the TR and s histograms show the skewed distributions with long-tail points to the right (right-skewed), while left-skewed distributions were observed for AR and v_m histograms (Fig. 9b, e).

One million random geometries

To demonstrate a potential application of ML in composite design and optimization, we applied the ML models to a much larger data set to determine the relations between the features and strength. First, one million random geometries (D_1M) were generated and imported to the decision tree to filter out the bad designs. In the second step, we used the SVR model to search for a relation between the features and strength. Figure 10 represents how a combination of features contribute to strength.

Fig. 10: This figure shows how a combination of features contribute to strength for one million random geometries.

Contour maps of composite strength at the elastic limit for D_1M. The contour shows the strength of a different combination of the geometrical features. The values of strength are normalized w.r.t. maximum values of strength in D_1M. The apparent noise in the contour maps is because the strength depends on four features, while each contour map shows variation in just two features.

Discussion

In order to test the dependency of the results on the size of D_training, the ML models were trained with three different sizes of the training data densities, that is, 50%, 60%, and 70%, while the D_v (10%) and D_test (20%) were kept fixed. Less than 2% discrepancy in results was observed in AUC and MSE for different D_training. Therefore, it was concluded that enough data points were generated from the finite element simulation. It is also worth mentioning that the decision tree regressor (DTR) was also tested for the regression problem. The MSE of the DTR in its best performance (depth of 7) was 3.4% that was more than 10 times higher than the SVR. Therefore, the SVR was selected for strength prediction.

Based on Fig. 6c, for the fixed value of AR, increasing the TR may cause HI and brick failure (bad design): this is because increasing the TR corresponds to thicker VI and larger strength of VI. For short bricks, VI failure controls the strength, as the stress required for HI failure (brick pull-out) and brick failure is smaller than the stress required to yield VI. However, for the designs with TR above one, as AR increases from two (brick length increases), the HI failure governs the composite strength. If the bricks are long (AR > ~23), the HI strength is higher than the stress required to break the bricks, such that the bricks fail prior to HI. In other words, longer bricks increase the stress generated in the bricks that can cause brick failure to occur. These results are consistent with the analytical results reported in ref. ³⁷, as the analytical model predicts no brick failure for AR = 5.

In Fig. 10, the white space in the TR-AR graph shows the bad designs that are filtered out by the decision tree. For a fixed AR, increasing TR corresponds to thicker VI. As the mortar sections become thicker, the applied stress required to cause them to fail increases. Thus, the strength increases with TR. This is not a valid conclusion for all the samples in D_1M. For instance, the maximum strength D_1M happens at AR = 40 and TR = −2. Therefore, each individual case needs to be investigated separately. No specific pattern in AR-s space was observed. Lower v_m increases the strength as the maximum strength was observed around 0.1–0.2 (Figs. 9e and 10). Figure 10 illustrates that TR and v_m have a profound effect on strength. For example, consider the case of AR = 10: in all cases, the vertical strength is varied by a factor of two upon varying TR and v_m between their upper and lower bounds. While the stiffness could be considerably improved by increasing the AR as it is reported in ref. ³⁷, the strength does not show a trend with brick size as no obvious trend between strength and brick size can be observed in v_m vs. AR contour map. However, there are points in the AR vs. v_m contour map with the relative strength higher than 0.9. Approximately 52% of these points have AR between 30 and 35, while 44% have AR between 40 and 45. The values of v_m and TR for these points are <0.5 and −1, respectively. FEA simulations also confirm that the implementation of these values in the design would result in higher strength.

The simulation time to calculate the stress–strain responses of 20,000 FEA models was ~50 h, while using the ML approach to predict the strength of one million geometries took only 6 s using the same computational resource. This comparatively short time demonstrates ML models’ capability to find the trend for the best design despite using a very small computational cost. Clearly, a much more detailed study is needed to understand trade-offs between all other design possibilities, other mechanical properties of brick-and-mortar, or mechanical behavior under different loading conditions.

The presented RVE draws inspiration from previous analytical and numerical studies for the micromechanical modeling of composite materials^{29,37,48,49,50}. For reference, the FEA model predictions are compared to the measured properties of the nacre-inspired synthetic Al₂O₃/PMMA (poly(methyl methacrylate)) composite²⁸, and an analytical model presented in ref. ³⁷. Using the properties for Alumina and PMMA reported in ref. ³⁷, and the pertinent composite details from ref. ²⁸ (v_m = 0.2, h = 8 μm, w = 50 μm, and t₂ = 1.5 μm), the presented model predicts a composite modulus of 111 GPa, close to the measured value of 115 GPa in the experiment. The analytical model in ref. ³⁷ predicts a composite modulus of 122 GPa. The slight discrepancy between analytical results³⁷ and the experiment²⁸ could be attributed to the following assumptions: (i) the horizontal mortar experiences pure shear and the vertical mortar sections experience pure tension, (ii) the bricks experience purely axial elongation, and (iii) the mortar is assumed infinitesimal in comparison to other dimensions. These assumptions may not be valid for brick–mortar structures with a large value of v_m, particularly metal/ceramic composites that usually have v_m larger than 40³⁷. Using the FEA, no simplifying assumptions need to be imposed on the geometry or mechanical behavior.

In this work, an ML approach was designed and implemented to model an elastic homogenization structure–property linkage in a brick-and-mortar composite material system. We propose an intelligent technique to predict the tensile strength. This technique is a combination of the FEA, SA, and ML. The SA was used for feature selection, while the ML was used for architecture tuning. Twenty thousand designs under different combinations of features were tested by the FEA for data set preparation. The FEA model describes the strength of an idealized composite, with bricks arranged in a staggered pattern that are perfectly bonded with mortar. These models were employed to train ML models. A large data set with one million geometries was imported into the trained ML models to further understand the relationship between each of those features and the mechanical behavior of the system. The results show that the thickness of vertical to horizontal mortar ratio (TR) and the aspect ratio of the brick (AR) are the main influencing features defining the design class, while mortar volume fraction (v_m) and shifting distance of the bricks (s) are not significantly different for each class. Moreover, these results emphasize the importance of simultaneously controlling TR and v_m. The high and low values of TR and v_m, respectively, assure the high strength, while low AR can be used for good design.

Methods

Brick and mortar model

All the constituents were assumed to behave elastically. The ratio of elastic moduli and strengths of the mortar to brick was assumed to be 0.5 based on the average values in the Ashby plot for metals and ceramics⁵¹. The von Mises stress was used to predict the yielding initiation of metal, and the maximum normal stress was used as the elastic limit for the ceramic phase, given the brittle nature of most ceramics. By comparing the maximum generated stress within metal and ceramic and knowing their strength, we can predict the initial failure mode that occurs at the limit of elasticity in the components. Post-yield analysis can be added to obtain information on the fracture and toughness in the composite. Poisson’s ratio for all the materials was considered to be 0.3. Geometrical symbols used in the model are presented in Table 2.

Table 2 Geometrical symbols in RVE.

t₁ and t₂ are the thicknesses of the vertical and horizontal mortar sections, respectively. LR is assumed to be one, without loss of generality. Moreover, all the parameters are normalized with respect to LR. The volume fraction of the mortar phase is derived from:

$$v_{\mathrm{m}} = \frac{{2(t_2 + t_1 \times h)}}{{\mathrm{WR}}}.$$

(2)

The RVE height is obtained by solving a system of equations:

$${\mathrm{TR}} = \log \left( {\frac{{t_1}}{{t_2}}} \right),$$

(3)

$${\mathrm{AR}} = \frac{w}{h},$$

(4)

$$1 = t_1 + w,$$

(5)

$${\mathrm{WR}} = 2(h + t_2).$$

(6)

AR is the aspect ratio of each brick and TR is the logarithmic thickness ratio of vertical and horizontal mortar sections. A logarithmic scale was used to better display the small and large values. AR, TR, v_m, and s were selected as independent geometrical features (dimensionless variables) that need to be quantified for constructing the RVE. Therefore, there are five unknown geometrical features, that is, t₁, t₂, w, h, and WR. The values of these unknown features can be obtained by solving the system of equations (Eqs. 2–6).

The dimensionless variable s is the shift in the staggered arrangement, divided by the RVE length = 1. These features vary continuously within their upper and lower limits (Table 3). The volume fraction v_m varies from 0.01 (~pure brick) to 0.99 (~pure mortar). For the model, we used the range v_m from 0.01 to 0.99 to avoid the extreme cases of pure brick and pure mortar. The shift in staggered arrangement s varies from 0 to the length of RVE that is 1. By virtue of symmetry, the results for the range of s between 0 (both layers of brick are aligned) to 0.5 is similar to 0.5 to 1 (both layers of brick are aligned). Therefore, the minimum and maximum values of s were assumed to be 0.01 to 0.5. TR = log (t₁/t₂) can vary from negative infinity to positive infinity. The finite element simulation revealed that the values of TR <−2 and >2 would not alter the results. AR = w/h is the aspect ratio of the bricks. A range of 2–50 was used based on experimental literature and reasonable brick aspect ratio. Based on our previous experimental work, the literature values and commercially available bricks, a typical range for AR is 5–20^28,29. Progress in additive manufacturing methods may be able to extend this range. We used a range of 2–50 as an extreme case.

Table 3 The upper and lower bounds of geometrical features.

The total number of geometry combinations is infinite. Therefore, we used sampling methods to generate the data set. To prevent under-coverage, multi-stage sampling was used. In the first stage, systematic sampling was employed to cover the entire design space by points with a specific distance in between. In the next step, a simple random sampling strategy selected the random values for the features in their predefined range (Table 3). The final data set contains >20,000 geometries.

Data generation

The ABAQUS FEA package with the implicit solvers implemented in ABAQUS/Standard⁵² was utilized to solve the stress and strain fields within the RVE. The RVE meshed with 132, 4-nodes plain-strain element CPE4R. Mesh sensitivity analysis showed that four times larger mesh density had <3% discrepancy in predicted stress and strain values. To analyze different geometrical configurations an algorithm capable of automatic generation of ABAQUS script files was implanted. This procedure was carried out using MATLAB⁵³. The FEA simulations were run 20,000 times on the generated RVE geometries using the presented algorithm. In the final step, a data set (D) containing geometrical features values and the FEA results was created.

ML model

The ML calculations were performed using Scikit-learn⁴⁷, the ML library in Python. The decision tree classification algorithm was selected because of its high interpretability and good performance⁵⁴. A decision tree represents the features in the form of a tree. We trained decision tree models with binary information to estimate their ability to reproduce actual performances based on limited D_training. The classification was done through the decision tree with its leaves representing different features conditions. The entropy evaluation function was chosen as the criterion for the branching process. The geometrical features and their classes (good or bad) were assigned as inputs and outputs for the decision tree.