Modeling the dynamics and spatial heterogeneity of city growth

Abstract

We propose a systems model for urban population growth dynamics, disaggregated at the county scale, to explicitly acknowledge inter and intra-city movements. Spatial and temporal heterogeneity of cities are well captured by the model parameters estimated from empirical data for 2005–2019 domestic migration in the U.S. for 46 large cities. Model parameters are narrowly dispersed over time, and migration flows are well-reproduced using time-averaged values. The spatial distribution of population density within cities can be approximated by negative exponential functions, with exponents varying among cities, but invariant over the period considered. The analysis of the rank-shift dynamics for the 3100+ counties shows that the most and least dense counties have the lowest probability of shifting ranks, as expected for ‘closed’ systems. Using synthetic rank lists of different lengths, we find that counties shift ranks gradually via diffusive dynamics, similar to other complex systems.

Introduction

Early studies based on analyses of empirical data and models suggested consistent power-law distribution of city populations^1,2,3,4,5, but the robustness (and the existence itself) of the empirical Zipf’s law has been challenged. For instance, the power-law exponent may depend on the country of study⁶, the definition of city⁷, the period under consideration⁸ and the estimation methods⁶, as well as tempering or cutoff observed in the lower- or upper-tail of the distribution^7,9. More recent analyses provide theoretical and empirical basis to explain such deviations among sets of cities. Bettencourt and Zund¹⁰ focus on the dynamic process of demographic growth plus the structure of migration flows to analyze the stationary distribution of city sizes. They show that symmetrical flows lead to Zipf’s law at the steady-state, while asymmetric flows might lead to other distributions. Verbavatz and Barthelemy¹¹ analyzed empirical data for four countries (U.S., Canada, UK, France) to propose a dynamic stochastic model for city population growth, and showed that rare and extreme migratory events are crucial in shaping the growth of cities, which in turn agrees with¹⁰.

In Verbavatz and Barthelemy¹¹ model, inter-city migratory flows are approximated by a distance-free model that depends only on the population sizes of the origin and destination cities. This model assumes that net flows are asymmetrical, which include migratory shocks that ultimately shape the growth of cities. However, Metropolitan Statistical Areas (MSAs) in the U.S. are composed of multiple counties, ranging from 1 to 29. In our study of domestic population flows in the U.S.¹², we showed that intra-city net flows trend from higher to lower density counties within the same city. Further, the internal redistribution of people within cities was found to be an important driver of the population increase in most external counties, thus being an important factor of urban expansion.

Migration patterns at the micro-level are usually studied under the heading of residential mobility, which helps us to understand why people move¹³. In a recent study, Frost shows that mobility is declining over the years, and that housing is the main reason behind local moves while employment is the main reason behind long-distance moves¹⁴. In a review of intra-urban residential mobility, Quigley and Weinberg¹⁵ present a description of the most important determinants of intra-metropolitan mobility, among which is family life cycle. Referring to the conceptualization of Hawley¹⁶, the effects of family life cycle on mobility can be summarized in the following steps: (i) a young couple starts the married life in an apartment; (ii) the couple moves to a small house as they have children; (iii) the family moves to a larger house in the suburbs as the family reaches its maximum size; (iv) the couple moves close to central city, to a small house, when the children leave to live on their own. Indeed, this conceptualization is somewhat supported by the studies of Plane et al.¹⁷, Lee et al.¹⁸ and Dieleman¹⁹.

In this paper, we re-examine the growth dynamics of cities by spatially dis-aggregating domestic migration flows in the U.S. at the county level. Domestic migration is the dominant source of growth in high-income, low-fertility countries such as the U.S.: the magnitude of domestic netflows is higher than the magnitude of natural growth for about 76% of U.S. counties, and domestic netflows are on average nine times more intense than natural growth (see Supplementary Fig. 1). We expand on the growth equation of cities¹¹ to include migration flows between counties within the same city (intra-city flows). The choice of counties as a proxy for urban unit relies on the data availability for county-to-county migration flows provided by the U.S. Census²⁰. Population and land-use data (and other urban metrics) are indeed available at finer spatial scales^21,22, but are not suitable for our analyses of intra- and inter-city populations flows with identity of the origin and destination counties for the flows.

Our approach explicitly considers cities as heterogeneous dynamical systems in terms of spatial and temporal patterns, with anisotropic flows contributing to population growth in counties within cities. We consider the heterogeneity of cities as captured by the spatial patterns of population density distribution^21,22,23, to examine cities undergoing different rates of population growth and expansion. We also examine rank-shift dynamics of population densities of counties resulting from differential population growth, contrasted with that of cities exhibiting sudden shifts in their ranks¹¹.

Our analyses of the empirical data for U.S. migration flows involved two stages. In the first stage, we analyzed annual estimates of flow data collected from 2015 to 2019 to study their spatial heterogeneity within 46 U.S. cities, each with at least six counties, and comprising a total of 469 counties (see Supplementary Fig. 2). The 2015–2019 period corresponds to the most recent 5-year migration flow files released by the American Community Survey (ACS)²⁴. A metro area with n counties has n(n − 1)/2 different netflow vectors, one for each pair of counties. Our analysis is restricted to n ≥ 3 because the gravitational model used to describe intra-city netflows has three free parameters. Here, we focus on the set of metro areas with n ≥ 6 (twice the lower bound) that offers more robust estimates to intra-city parameters (avoid overfitting), which accounts for about 15% of counties and 39% of population of the U.S., and reduce the dispersion of the distribution of intra-city parameters.

In the second stage, we extended these analyses for the 2005–2019 period, based on the estimated mean annual flows, to examine temporal trends in population flows. Our choice for the 2005–2019 is based on the availability of ACS 5-year migration flow files: the first flow file corresponds to the 2005–2009 period, and the last corresponds to the 2015–2019 period. In our analyses, we only consider flows between the 469 counties within the set of 46 metro areas. For this reason, in the following discussion we use the terms city and metropolitan statistical areas interchangeably.

In the following, we first present a stochastic system model for spatio-temporal dynamics of inter-county migration flows, followed by a quantitative analyses of the empirical flow data based on estimation of the key parameters in the model and the statistical structure of these parameters. We then examine two other aspects of the county-level population growth dynamics, based on the county population density: a comparison of temporal shifts in intra-city spatial structure across the selected cities; and rank-shift dynamics. We close with a discussion of the implications of our model-data analyses for understanding urban population growth dynamics in the U.S., as well as the limitations arising from available population flow data and constraints for projections of likely changes or extensions to population flow dynamic in other countries.

Results

City population dynamics

Let us consider a system composed of a set of cities within a country. The growth equation of a city k within this system can be written as

$$\frac{d{S}^{k}}{dt}=\eta {S}^{k}+\mathop{\sum}\limits_{l\in {N}^{k}}{{{{\mathcal{J}}}}}^{k\to l}-{{{{\mathcal{J}}}}}^{l\to k},$$

(1)

in which η is the out-of-sytem growth, accounting for births minus deaths and international migration, and ${{{{\mathcal{J}}}}}^{k\to l}$ represents migratory flows from city k to city l. The sum in the second term on the right side of Eq. (1) accounts for population growth due to netflows exchange with the set of ${N^{k}}$ cities within the system.

Verbavatz and Barthelemy in ref. ¹¹ find that “interurban migratory shocks dominate city growth”. They show that inter-city flows are well approximated by a distance-free model as ${{{{\mathcal{J}}}}}^{k\to l}={{{\mathcal{I}}}}{({S}^{k})}^{\nu }{({S}^{l})}^{\nu }{x}^{k\to l}$, in which ${{{\mathcal{I}}}}$ is a constant, ν is an exponent capturing the influence of the population of origin and destination cities in driving the flows, and x^k→l captures high-order effects such as the role of distance and random fluctuations. The total netflows of a given city k is then written as ${\sum }_{l\in {N}^{k}}{{{{\mathcal{J}}}}}^{k\to l}-{{{{\mathcal{J}}}}}^{l\to k}={{{\mathcal{I}}}}{({S}^{k})}^{\nu }{\sum }_{l\in {N}^{k}}{({S}^{l})}^{\nu }({x}^{k\to l}-{x}^{l\to k})$, and the impact of netflows on the city is captured by the rescaled variable ${{{{\mathcal{X}}}}}^{kl}={({S}^{l})}^{\nu }({x}^{k\to l}-{x}^{l\to k})=({{{{\mathcal{J}}}}}^{k\to l}-{{{{\mathcal{J}}}}}^{l\to k})/{{{\mathcal{I}}}}{({S}^{k})}^{\nu }$. Note that ${{{{\mathcal{X}}}}}^{kl}$ depends on the sum of random variables x^k→l and x^l→k, thus the direction and intensity of netflows are driven by random fluctuations. They find that ${{{{\mathcal{X}}}}}^{kl}$ follows a heavy-tailed distribution, and that the sum of rare and extreme fluctuations (viz. rescaled netflows at the tail of the distribution of ${{{{\mathcal{X}}}}}^{kl}$) shape the growth of cities.

The aforementioned approach does not acknowledge the intra-city spatial heterogeneity, which has been addressed by urban metrics such as population density^25,26 and land use²⁷. Here, we acknowledge the intra-city spatial heterogeneity and model population growth at a more disaggregated level, viz., county level. We focus our attention on the growth of counties because this is the smallest geographic region having data regarding inflows and outflows. Nevertheless, the framework we present in the following section can be extended to smaller regions once migratory flow files are available.

County population dynamics

The growth of a county within a given city is given by (neglecting international migration flows):

$$\,{{\mbox{County growth = natural growth + intra-city moves + inter-city moves}}}.$$

Consider the population growth of county i within city k. By defining ${Y}_{j\to i}^{k}$ as the flow from county j to county i in which both counties belong to k, and J_p→i as the flow from county p in city m to county i in city k, for all cities m such that m ≠ k, we can write:

$$\begin{array}{rcl}\frac{d{S}_{i}^{k}}{dt}&=&\eta {S}_{i}^{k}+\mathop{\sum}\limits_{j\in k}\left({Y}_{j\to i}^{k}-{Y}_{i\to j}^{k}\right)+\\ &&+\mathop{\sum}\limits_{m:m\ne k}\mathop{\sum}\limits_{p\in m}\left({J}_{p\to i}-{J}_{i\to p}\right),\end{array}$$

(2)

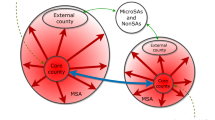
in which ${S}_{i}^{k}$ is the population of county i in city k, t is the time instant and η is the natural growth rate. The flows contributing to the population growth of county i are represented in Fig. 1. In this schematic figure, the intensity of the background color represents the population density of the counties. The black arrows represent intra-city netflows (${Y}_{j\to i}^{k}-{Y}_{i\to j}^{k}$) between counties within the same city, and blue/green arrows represent inter-city netflows (J_p→i − J_i→p) between counties from different cities.

Fig. 1: Intra- and inter-city netflows contribution to the growth of counties.

This schematic figure illustrates the components of domestic migration affecting the growth of counties of Atlanta and Charlotte metro areas. Intra-city netflows are represented by black arrows. Inter-city netflows from Atlanta to Charlotte are represented by blue arrows, and the green arrows represent inter-city netflows in the opposite direction. The opacity and width of the arrows are proportional to the intensity of the netflows. The background color resembles the population density of the counties, in which denser counties have darker colors. Intra-city netflows have a trend from higher to lower density counties, and the most intense inter-city netflows were directed to Charlotte. This figure was based on migration flow data of the 2015–2019 period.

In order to model intra-city netflows, we hypothesize that distance plays an important role in determining the magnitude of netflows and that population density is crucial in determining the direction of the netflows. The first hypothesis is based on the fact that the highest share of domestic flows is local and decays with distance (Fig. 2). The second hypothesis is based on the results reported in ref. ¹², which shows that the highest share of intra-city netflows are directed to lower density counties for more than 90% of the cities considered, thus indicating that the redistribution of people within a given city is asymmetrical. As a consequence, the term corresponding to intra-city netflows in Eq. (2) is written as:

$$\mathop{\sum}\limits_{j\in k}\left({Y}_{j\to i}^{k}-{Y}_{i\to j}^{k}\right) =(2{{{{\mathcal{F}}}}}^{k}-1){H}^{k}\left(\mathop{\sum}\limits_{{\rho }_{i} < {\rho }_{j};j\in k}\frac{{({S}_{i}^{k})}^{{u}^{k}}{({S}_{j}^{k})}^{{u}^{k}}}{{d}_{ij}^{{\sigma }^{k}}}-\mathop{\sum}\limits_{{\rho }_{i} > {\rho }_{j};j\in k}\frac{{({S}_{i}^{k})}^{{u}^{k}}{({S}_{j}^{k})}^{{u}^{k}}}{{d}_{ij}^{{\sigma }^{k}}}\right).$$

(3)

Fig. 2: The highest share of domestic migration is local (d ≤ 100km) in the U.S., and the distributions of intra-city parameters follow a normal distribution.

About 86% of the domestic grossflows between two counties (a) are found within a distance d≤100km, and about 92.3% of domestic netflows is within a 100 km radius (b). After d = 100 km, the probability of grossflows and netflows decay with a power-law with cut-off about 10⁴. We consider distributions of fraction of flows from higher to lower density counties ${{{{\mathcal{F}}}}}^{k}$ (c), county population’s exponent u^k (d) and distance’s exponent σ^k (e) of all cities k in our system. The empirical distribution of each parameter in black is characterized by mean and standard deviation as shown. The curves in red correspond to the Gaussian pdf with respective mean and standard deviation. The goodness of fit is addressed by the KS-test, with KS and p values (under the null hypothesis that both distributions are equal) being reported in the panels.

Intra-city netflows trend from higher to lower density counties is captured by the fraction of netflows to lower density counties ${{{\mathcal{F}}}}$. Acknowledging that each city k has its own internal migration pattern due to a multitude of factors²⁸, we assume that ${{{{\mathcal{F}}}}}^{k}$ depends on the city k (see Supplementary Table 1). We also assume that exponents u^k and σ^k, which captures the strength of county population and distance between counties in intra-city flows, depend on the city k under consideration. The variable H^k is a constant.

The term $(2{{{{\mathcal{F}}}}}^{k}-1)$ modulates and directs netflows within the same city, thus accounting for the resulting population growth due to intra-city netflows. Note that there is no trend if ${{{{\mathcal{F}}}}}^{k}=0.5$. In this case, intra-city flows are random and the netgrowth is zero on average. The first sum on the right side of Eq. (3) represents the inflow of people coming from counties j, within the same city k, with higher population density ρ (i.e. ρ_i < ρ_j). The second sum on the right side of Eq. (3) represents the outflow of people to lower population density counties j.

Inter-city netflows, capturing flows between counties from different cities, do not have a trend with respect to origin and destination county population densities¹². In this sense, we follow¹¹ and approximate inter-city flows J_p→i from county p in city m to county i in city k with the distance-free model ${J}_{p\to i}={({S}_{i}^{k})}^{\nu }{({S}_{p}^{m})}^{\nu }({x}_{p\to i})$ (see the section “City population dynamics”). The exponent ν captures the strength of county population size in the flows between two counties, and x_p→i is a random variable accounting for higher order effects. In light of this, inter-city netflows is written as

$$\mathop{\sum}\limits_{m:m\ne k}\mathop{\sum}\limits_{p\in m}\left({J}_{p\to i}-{J}_{i\to p}\right) = I{({S}_{i}^{k})}^{\nu }\mathop{\sum}\limits_{m:m\ne k}\mathop{\sum}\limits_{p\in m}{({S}_{p}^{m})}^{\nu }({x}_{p\to i}-{x}_{i\to p}),$$

(4)

in which I is a constant.

Interestingly, Eq. (4) shows us that the direction and the intensity of inter-city netflows between counties i and p depend on the difference between random variables x_p→i and x_i→p. By denoting ${X}_{p\to i}^{m}={({S}_{p}^{m})}^{\nu }({x}_{p\to i}-{x}_{i\to p})$, we see from Eq. (4) that ${X}_{p\to i}^{m}=({J}_{p\to i}-{J}_{i\to p})/I{({S}_{i}^{k})}^{\nu }$, thus ${X}_{p\to i}^{m}$ captures the relative impact of migratory flows in a given county when netflows are adjusted by population. Note that J_p→i represents inter-city inflows to county i, while J_i→p represents inter-city outflows from county i. In this sense, rescaled netflows ${X}_{p\to i}^{m}$ can be positive or negative, with distributions shown in Supplementary Fig. 3. In contrast to the distribution of rescaled netflows between different cities, which are well approximated by a heavy-tail distribution (viz. power-law)¹¹, the distribution of rescaled netflows between counties from different cities is exponentially bounded (viz. lognormal distribution), thus suggesting that counties do not experience rare and extreme migratory events as cities. As pointed out in ref. ¹², counties have fixed boundaries while city boundaries are dynamic, expanding and absorbing adjacent counties if needed. Besides, extreme migratory shocks to a given city are dissipated among the different counties, in a ‘spill over’ effect¹².

For convenience, we can write the total inter-city netflows to county i (Eq. (4)) as

$$\mathop{\sum}\limits_{m:m\ne k}\mathop{\sum}\limits_{p\in m}\left({J}_{p\to i}-{J}_{i\to p}\right) = I{({S}_{i}^{k})}^{\nu }\mathop{\sum}\limits_{m:m\ne k}\mathop{\sum}\limits_{p\in m}{X}_{p\to i}^{m}=I{({S}_{i}^{k})}^{\nu }{N}_{i}{\xi }_{i},$$

(5)

in which ${\xi }_{i}=(1/{N}_{i}){\sum }_{m:m\ne k}{\sum }_{p\in m}{X}_{p\to i}^{m}$ and N_i is the number of counties from other cities exchanging people with county i. We find that the distribution of ξ_i, which can be seen as the mean netflow per interacting county, is well approximated by a skew-normal distribution (see Supplementary Fig. 4a). The asymmetry in the distribution ξ_i is caused by positive netflows to counties with lower population. If we consider the distribution of ξ_i from counties with population higher than 50000, the resulting distribution is well approximated by a normal distribution (see Supplementary Fig. 4b). In summary, the results from our analysis of empirical migration flow data suggest that (1) counties with lower population are more likely to have positive netflows and (2) ξ_i can be approximated by a random variable normally distributed.

The number of counties N_i follows a non-linear relationship with the county size ${S}_{i}^{k}$, as shown in Supplementary Fig. 5, so that ${N}_{i}=C{({S}_{i}^{k})}^{\beta }$. Thus we rewrite Eq. (5) as

$$\mathop{\sum}\limits_{m:m\ne k}\mathop{\sum}\limits_{p\in m}\left({J}_{p\to i}-{J}_{i\to p}\right)=D{({S}_{i}^{k})}^{\gamma }{\xi }_{i},$$

(6)

in which exponent γ = ν + β and D is a constant given by D = IC. The log-linear fitting of inter-city flows gives us ν = 0.29 and I = 0.02.

Eqs. (3) and (6) allow us to rewrite Eq. (2) for county growth as:

$$\begin{array}{l}\frac{d{S}_{i}^{k}}{dt}=\eta {S}_{i}^{k}+\\ \,+(2{{{{\mathcal{F}}}}}^{k}-1){H}^{k}\left(\mathop{\sum}\limits_{{\rho }_{i} < {\rho }_{j};j\in k}\frac{{({S}_{i}^{k})}^{{u}^{k}}{({S}_{j}^{k})}^{{u}^{k}}}{{d}_{ij}^{{\sigma }^{k}}}-\mathop{\sum}\limits_{{\rho }_{i} > {\rho }_{j};j\in k}\frac{{({S}_{i}^{k})}^{{u}^{k}}{({S}_{j}^{k})}^{{u}^{k}}}{{d}_{ij}^{{\sigma }^{k}}}\right)+\\ \,+D{({S}_{i}^{k})}^{\gamma }{\xi }_{i}.\end{array}$$

(7)

Interestingly, the model for population growth of cities k is recovered by aggregating the flows contributing growth of its ${{{{\mathcal{N}}}}}^{k}$ counties, so that

$$\frac{d{S}^{k}}{dt}=\eta {S}^{k}+D{\phi }^{k},$$

(8)

in which ${\phi }^{k}={\sum }_{i\in {{{{\mathcal{N}}}}}^{k}}{({S}_{i}^{k})}^{\gamma }{\xi }_{i}$. This expression shows that while intra-city flows are important to describe the heterogeneous growth of urban units (i.e. counties) within cities, the growth of a city as a whole is represented by natural growth and inter-city migratory events¹¹.

Parameters estimation and heterogeneity

The proposed county-level population dynamics model contains five key parameters: ${{{\mathcal{F}}}}$, u, σ, ν, and β. The parameters ${{{\mathcal{F}}}}$, u, σ are used to describe intra-city flows, thus the heterogeneity of cities is represented by the fact that each city k has its own set of values: ${{{{\mathcal{F}}}}}^{k}$, u^k, σ^k. The parameter ${{{{\mathcal{F}}}}}^{k}$ of a city k is directly computed from the empirical data by doing ${{{{\mathcal{F}}}}}^{k}$ = (sum of netflows, within city k, from higher to lower density counties) / (sum of netflows within city k), thus ${{{\mathcal{F}}}}\in [0,1]$ captures the fraction of intra-city netflows to lower density counties. Note that netflows are always directed from higher to lower density counties when ${{{\mathcal{F}}}}=1$, but are randomly directed towards any county if ${{{\mathcal{F}}}}=0.5$.

The exponent u captures the strength of asymmetry in county population (S) driving intra-city netflows within a given city, with u≤1, suggesting a sub-linear increase with increasing S. The inverse dependence of intra-city netflows on distance between county centroids is depicted by exponent 0 ≤ σ ≤ 2, with σ = 0 implying flows are agnostic to separation distances (as was found by Verbaratz & Barthelemy¹¹ for inter-city flows), whereas larger values suggest intra-city netflows diminish nonlinearly with distance. For each city k, the magnitude of netflows between any pair of counties i, j within the city is approximated by the gravitational model (see Eq. (3)), and the parameters u^k and σ^k are estimated from empirical data using log-linear regressions with parameters shown in Supplementary Table 1.

Although each city is unique, with a particular set of parameters (Supplementary Table 1), the statistical distributions of model parameters across different cities during the same period are well approximated by Gaussian distributions, with CV < 0.52 for u and σ, and CV ~ 0.24 for ${{{\mathcal{F}}}}$ (Fig. 2). These results suggest that while each household decisions are driven by a multitude of factors to optimize costs-benefits, the macro-scale behavior of all counties and cities can be approximated as a random process (Gaussian pdf).

Inter-city flow parameters ν and β are estimated using flow data between counties from different cities. To obtain ν, the magnitude of inter-city flows is approximated by the distance-free model (see Eq. (4)), and the value of ν is estimated using log-linear regressions with parameters shown in Supplementary Table 3. Parameter β is obtained from the non-linear relationship between the number of counties from other cities N_i exchanging people with county i and its population. The results of log-linear fittings for different time periods are also presented in Supplementary Table 3. For both sets of parameters (viz. intra- and inter-city flow parameters), the range in temporal (2005–2019) variability is small enough (Supplementary Figs. 6, 7 and 8) that mean parameters values might prove to be sufficient to predict population flows (Supplementary Tables 2, 3 and 4).

We find that the population dynamics of the counties can indeed be well approximated by proposed model (Eq. (7)) with parameter values given by their time-averaged values (see Supplementary Tables 2 and 4). For 2010 (Fig. 3, panels a and b), the relative error reveals that ~63% of the counties population is estimated with a percentage error lower than 0.05, while ~89% and ~97% of the counties, population is estimated with a percentage error lower than 0.15. For 2015 (Fig. 3, panels c and d), the relative error reveals that population for ~40% of the counties estimated with a percentage error lower than 0.05, while county population for ~68% and ~85% is estimated with a percentage error lower than 0.10 and 0.15, respectively. The mean of the absolute percentage errors (MAPE) are MAPE = 0.05 for 2010 and MAPE = 0.08 for 2015, indicating that the errors of the estimates increases slightly with time. Therefore, the model with fixed parameters, set at their time-averaged values, captures the overall population dynamics of the system of counties for the time period we considered here. A word of caution is in order; using these parameters to make projections at longer time intervals (i.e. >10 years when starting in 2005) is infeasible for lack of requisite empirical data. Our model may generate unreliable results if the underlying drivers of inter-county flows undergo rapid (sudden) shifts, as they do for the case of inter-city flows.

Fig. 3: Model with parameters given by their time-averaged values performs well at the system level.

a, c The estimated population density as function of the empirical population density in 2010 (a) and 2015 (c) of the 469 counties belonging to the 46 cities under consideration. The model starts at 2005 with the population density of the counties in this year as initial condition. Each gray dot represents a county. The x-axis is binned, and the mean and the error bars are colored green if the line y = x lies within the 95% confidence interval, otherwise mean and error bars are colored red. b, d The relative error of the estimates. The population estimate for each county was averaged over 100 independent runs.

Population density patterns

There are several models for describing the spatial heterogeneity in various urban metrics^23,29,30. Among them, the most used are the negative exponential²⁵ for population density, and the inverse power-law²⁶ for describing land-use²⁷. The negative exponential model assumes that cities are monocentric, isotropic, with growth occurring via spatio-temporal diffusive processes^27,31. However, the geographic expansion of cities are not radially symmetric³², but constrained by geographic, political, and land-use/land-cover constraints^21,22. Figure 4 shows the spatial profiles for relative population density ρ_r = ρ/ρ_C, in which ρ is the population density of a given county and ρ_C is the core county density, for the top nine cities in the U.S. We observe that each city is characterized by a different exponential decay, but with two trends.

Fig. 4: The heterogeneity of cities is captured by the exponential decay of the population density with distance.

a The relative population density (ρ_r), given by county’s population density scaled to that of the core county (ρ_C), as function of distance from the core county (d_r). Colored dots represent the top nine most populous cities with more than five counties, shown in detail in b–j, and gray dots represent the remaining 37 metro areas. The relative density ρ_r can be approximated by the exponential function ${\rho }_{r} \sim {e}^{-\omega {d}_{r}}$, in which ω and R² are indicated in the panels. In b–j, the size of the dots are proportional to the land area of the counties.

First, the estimated values of the slope, ω, for a given city do not change over the time period. Differences between ω estimates for 2015 and 2005 are not statistically significant: for all cities, we can not reject the null hypothesis that both estimates belong to same distribution since p-value ≫ 0.10 (t-test). In this context, these cities seem to have reached a quasi-steady state³³ in which population density profiles are approximately constant. All U.S. counties underwent a mean relative growth of about 7% from 2005 to 2015 (Supplementary Fig. 9). Our findings indicate that this growth had only minor affect on the stability of the population density profiles of the 46 U.S. cities included in our analyses here.

Second, the ω values are different among the cities, but with variable explanatory performance of the model (R²) among cities. The spatial resolution of the mean density values depends on the number of counties constituting a city, the variable county areas, the built-up areas of a county, and the geographical distribution of households. For cities experiencing different levels of anisotropic land-use expansion and densification^22,23,34,35, it is not surprising that some are better explained by the exponential model than others²³.

County rank dynamics

Cities rise and fall in terms of their attractiveness and economic activity over time. Batty³⁶ points out that the rise and fall of cities, captured by rank-plots, are associated with rare, extreme population flow events. In this context, migratory shocks described by Lévy fluctuations emerge as a better explanation for the “turbulent properties of the dynamics of cities through time”¹¹ than proportional growth models since a rank analysis reveals that the model in¹¹ predicts rank volatility closer to the empirical rank volatility.

The mechanisms behind rank-shifts in diverse systems were explored by Iñiguez et al.³⁷. They analyzed the rate at which new elements enter or leave a ranked list of fixed size, and classified diverse complex systems as being ruled by rank-shifts as Lévy walk, diffusive or replacement regimes. Unlike cities, counties do not go through dramatic population changes via migratory shocks. We have shown¹² that inter-city flows are dissipated among counties within the same city, so that the distribution for ξ_i follows a Gaussian distribution. Consequently, we expect a diffusive regime for county rank-shifts in which rank changes are gradual and spatial patterns within cities are unlikely to change abruptly. Here, we examine the temporal evolution of counties in terms of rank dynamics, using mean population density as the metric for ranking. Other metrics such as county population could have been used, but density accounts for differences in populations and areas. Nevertheless, the analysis with population as metric for ranks leads to similar conclusions.

We create a rank list of length N₀ = N, in which N is the number of counties in the U.S., and investigate probability of rank shift between consecutive times (C) in each rank position (R) in Supplementary Fig. 10. We observe that C is lower at the top and at the bottom of the rank list, suggesting that the counties at these positions are more stable and less susceptible to rank shifts. As expected, this behavior is consistent with the behavior of a closed system since we are considering a rank comprising all the counties in our set.

The rank dynamics can be further explored by creating synthetic ranking lists of lengths N₀ < N to mimic the behavior of open systems. In this sense, here we create synthetic lists of sizes N₀ = 100, 200, 300, …, 3100 to analyze systems with different levels of openness. The rank dynamics of open systems is then captured by the following variables: the number of different counties N_t that appeared at least once among the top N₀ counties until time t, the flux F_t given by the probability that a county enters or leaves the list of the top N₀ counties at time t, and the rank turn over o = N_t/N₀³⁷.

The relationship between the rank dynamics and the openness of the synthetic systems is show in Fig. 5. We observe a monotonic growth of o_t with t, which is less intense as N₀ increases (panel a). In the case N₀ = N, we observe o_t = 1 irrespective of the time instant since no counties enters or leaves the rank list that already comprises all the U.S. counties. By defining $\dot{o}=({o}_{t = 10}-{o}_{t = 0})/10$ and F = 〈F_t〉, the linear dependence of $\dot{o}$ on F suggests that the dynamical properties of rank shifts continuously change as the system transitions from being more (low N₀) to less (high N₀) open (panel b).

Fig. 5: Rank shifts are ruled by a diffusive process.

a The turn over rate o_t as function of t for N₀ = 100, 500, …, 3137. Open systems are more prone to the entrance of new elements, thus o_t=10 is higher for more open systems. b $\dot{o}$ can be approximated by the model $\dot{o}=\alpha F$, indicating that there is a continuous transition from open to closed systems as the rank length increases from N₀ = 100 (blue dot) to N₀ = 3100 (red dot). c The reescaled parameters τ_r and d_r fall into the universal curve τ_rd_r = 1, as observed in open systems³⁷.

In ref. ³⁷, the authors propose a model for F and $\dot{o}$ to explore the mechanisms driving the rank dynamics, given by:

$$F=1-{e}^{\nu }[p+(1-p){e}^{-\tau }]{{{\:\rm{and}}}}\,\dot{o}=\nu \frac{\nu +\tau }{\nu +p\tau },$$

(9)

in which p = N₀/N is the fraction of the system size comprised by the length of the rank list. Panel c of Fig. 5 shows estimated parameters of this model (ν and τ) for each synthetic list re-scaled as ${\tau }_{r}=\frac{\tau }{p(1-p)\dot{o}}$ and ${\nu }_{r}=\frac{\nu -p\dot{o}}{\dot{o}}$, suggesting that the relationship between τ_r and ν_r is well approximated by the universal curve τ_rν_r = 1. The average probability that a county changes its rank via diffusive process (W_Diff = e^−νe^−τ) is much higher than changes via Lévy walk (W_Levy = e^−ν(1 − e^−τ)) and via replacement (W_Repl = 1 − e^−ν)³⁷, suggesting that the rank dynamics is driven by smooth changes in the population density of counties. The rank volatility obtained with the model we propose here is closer to the empirical rank volatility than a null model in which counties have no exchange of people via inter- and intra-city flows (Supplementary Figs. 11 and 12). Thus, it is a step forward to a better understanding of the drivers of city growth.

Discussion

We develop a general system modeling approach to analyze city growth at the county level. The proposed model includes the intra-city redistribution of people that explicitly accounts for intra-city heterogeneities in population flows¹². This offers a mechanism to explain suburbanization and urban sprawl³⁸. The predictive performance of our model is conditioned to small fluctuations of the parameters around mean values. Our data analysis is focused on ACS county-to-county flow files. Each flow file contains annual flows obtained in 5-year time windows to offer more robust estimates of low-intensity flows, and usage of shorter time-spans could lead to larger deviations from migration trends.

Our choice of using data from metropolitan statistical areas to study city growth was based on the finest spatial resolution of flow data available (county level). Consequently, we have analyzed flows between counties within the same metro area (intra-city flows) and between counties belonging to different metro areas (inter-city flows). However, here we cannot quantify the spatial population heterogeneity within a given county, which is not homogeneously distributed. In fact, Supplementary Table 5 shows that the highest share of land area of the MSAs considered (besides New York and Boston) is rural. From the population perspective, Supplementary Table 6 shows that the highest share of MSAs population is urban, but rural population accounts for up to 39.4%. The urban population is split into urbanized areas (urban areas of 50,000 or more) and urban clusters (urban areas of at least 2500 and <50,000), thus the population of metro counties is spread among urban areas occupying small shares of land. In spite of the constraints of our analysis at the aggregate level of a county, the same framework we propose here could be used to study flows at smaller geographic units if data were available at finer spatial resolution.

We have covered the 2005–2019 period. For this period, we have shown that mean values capture well the parameter’s trends. However, if the system of cities undergoes a dramatic shock or event causing disruptive fluctuations in the estimated parameters, then the predictive performance of the model would be compromised. The consideration of longer time-spans could compromise the performance of the model as well because of changes not only in migration trends (see Supplementary Fig. 13) but also in county/city boundaries. Nevertheless, the descriptive performance by means of understanding the drivers of city and county growth, viz. intra- and inter-city flows, would not be compromised since the parameters of the model can be estimated for any time instant irrespective of temporal trends.

The highest share of migration flows in the U.S. occurs within a county and a state, with about 90% of domestic flows occurring within a 100 km radius (Fig. 2). Given that employment is the main reason behind long-distance / inter-city moves¹⁴, the distance-agnostic flow model performs well at explaining inter-city moves. On the other hand, the main reasons behind local/intra-city moves are housing and family¹⁴, so distance plays an important role. In this scenario, the gravitational model, which has been used in similar contexts of urban migration^39,40, emerges as a natural candidate for describing intra-city flows. Consequently, the performance of the model as presented here is also conditioned on the stability of the drivers of flows. If the reasons behind long-distance and local moves change, then distance may play a different role in domestic flows, thus compromising the utility of the flow models used here.

Our findings indicate that the population density profiles for counties within cities are well described by negative exponential decays which are stable over the time period considered, signaling either that cities reached a quasi-steady state in which natural growth, inter- and intra-city flows balance each other so counties within the same city grow at a rate proportional to population, or that the period studied here is too small compared to the time scale in which changes in population density occur. A similar conclusion is reached by our analysis of rank-shift dynamics³⁷. Using population density as a metric for rank classification, we find that rank shifts are more likely to be characterized as a diffusive regime, thus supporting the findings that the changes in population density profiles are gradual and that inter-city flows are dissipated at county level, so that county populations do not experience extreme migratory shocks.

Socioeconomic level increases segregation between rich and poor⁴¹ and affects mobility patterns of high and low income classes²⁸. Our model was built on empirical migration flow data of the U.S., in which the highest share of population live in highly urbanized areas and inter- and intra-cities are the majority of migratory flows¹². In this context, the approach presented here can be extended to other urbanized countries whose domestic flows are dominated by inter- and intra-city flows as well. For steadily and rapidly urbanizing countries, as defined in ref. ⁴², the distribution of ξ_i should be asymmetrical because of migratory trends from low to high urbanized areas. However, the model presented here should be used with caution since: (1) population flows can be dominated by rural-urban and rural-rural migratory flows, which are not included in our model; (2) distance may be a more important factor in driving inter- and intra-city moves. The modeling of urban areas from low income countries that have more than 60% of population living in small cities or neighboring areas⁴³ should include rural-urban and rural-rural migratory flows.

Although population density patterns might be spatially anisotropic, the overall behavior is well approximated by a negative exponential trend, suggesting that the growth of intra-city counties is ruled by diffusive processes^25,27. Several complex factors affect the redistribution of people within a city such as economic activity, housing needs, urban policies, culture, etc.³⁸. This heterogeneity is captured by the finding that each city is well approximated by a different exponential decay.

City-level population dynamics are explained by sudden shifts (Lévy shocks¹¹) driven by one or more external drivers, such as financial, social-political, disasters, job markets, that either increase the attractiveness of cities at both local and regional scales. Recent analyses¹² show that when migration flows are disaggregated the county level (cities with more than five counties), the heavy tails in Levy shocks are ‘tempered’ by dispersing flows within the counties in these cities, and they can be approximated as Gaussian pdfs. Here we find that rank-shift dynamics for these counties will exhibit the characteristics (and regimes) described in a recent Iniguez et al.³⁷, depending on whether system of counties we consider are treated either as closed systems or as systems with different degrees of openness. On one extreme is the closed system when we include all the U.S. counties (~3100), because no counties are added because of population growth. On the other hand, as the populations of cities continue to increase and the city area expands, spilling over to micropolitan counties in the surrounding areas (i.e., urban sprawl) via intra-city flows, the number of city counties continues to increase; thus we have an open system whose rank-shifts will most likely be described by diffusive process as we seen with the synthetic ranks we created here. However, these dynamics occur at longer timelines (multi-decadal, consistent with census data and reclassification).

Methods

Data collection

We analyze empirical data to unveil the dynamics of city growth. Migration flow data were used to characterize the distribution of intra- and inter-city domestic migration flows, and county population totals were used to extract components of resident changes, viz. births and deaths, to compute the natural growth.

Our analysis is restricted to the period 2005–2019. The two datasets used in this study, both from U.S. Census, are listed below:

• County-to-county migration flows data set. This dataset is a result of annual surveys conducted by the American Community Survey (ACS) and the Puerto Rico Community Survey (PRCS) in which “respondents age 1 year and older whether they lived in the same residence 1 year ago”²⁰. Results are reported over 5-years period in which flow estimates resemble annual number of movers.

• County population totals dataset. This dataset offers “population, population change, and estimated components of population change”⁴⁴. From this dataset, we extract births and deaths to compute the natural growth.