Effects of aberrations on 3D optical topologies

Abstract

Optical knots and links are nontrivial three-dimensional topologies consisting of trajectories of phase or polarisation singularities. They are theoretically predicted and experimentally observed in paraxial and nonparaxial regimes and in random and speckle fields. The topological nature of optical knots suggests that environmental disturbances should not alter their topology, hence becoming a resilient vector of information. However, the robustness of optical knots under typical disturbances encountered in optical experiments has not been investigated. Here, we provide the experimental analysis of the effects of optical phase aberrations on optical knots and links. We demonstrate that Hopf links, trefoil and cinquefoil knots are robust to misalignment and phase aberrations. The observed knots are obliterated for high aberration strengths and defining apertures close to the characteristic optical beam size. Our observations indicate these photonic topological structures as viable alternatives for both classical and quantum information processing noisy channels, where optical modes are not applicable.

Introduction

Linked or knotted structures can arise from optical fields as trajectories in the three-dimensional space of phase or polarisation singularities^{1,2,3,4,5,6,7,8,9,10}. For instance, a scalar paraxial optical field described by the wavefunction ψ(x, y, z), at a given plane z, can exhibit points of zero intensity where the phase is undefined¹¹. These singular points are characterized by a topological charge q given by the winding of the field’s phase around the singularity^4,6,11,12,13: q = 1/(2π)∮_L∇ψ ⋅ dℓ, where L is a closed loop around the singularity and dℓ the infinitesimal arc length. Stable singularities carry the minimal topological charge q = ± 1 and can evolve in space with the constraint of total topological charge conservation^12,14,15,16, i.e., singularity pairs, with individual components having opposite q, can annihilate each other or emerge from planes where no charge is present. This dynamics of creation and annihilation of pairs at different planes can result in singularity paths confined in the three-dimensional space and forming a closed trajectory¹⁷. These curves can be trivial loops, for instance, generated by two charges appearing in one plane and then re-joining each other upon free-space propagation¹⁸. However, it is now well-known that the wave equation allows for solutions where singularities can track linked or knotted trajectories^1,17. These solutions were originally found by perturbing high-strength vortex line singularities threaded by unstable loop singularities¹. Other approaches based on numerical optimization procedures and Laguerre-Gauss mode expansions^3,19,20,21 have been subsequently developed. More recently, it has been shown that specific optical knots can be generated by imposing weighted polynomials as boundary conditions on the field amplitude^22,23,24. This result, which still lacks a general proof²², is particularly intriguing since it may lead to a systematic approach for generating optical knots and links. This may prove extremely useful in implementing secure communications based on optical knots^23,24,25, and quantum money^26,27.

While some kinds of singularities, like high-order topological charges and some types of caustics²⁸, can be structurally unstable, knots and links formed by elementary singularity paths are mathematically stable. Indeed, knots and links are topologically robust objects since they cannot be smoothly deformed into each other. For a knot to change type, a mathematical transformation should reach a point in parameter space where the knot is singular, i.e., self-intersecting. An optical knot is thus expected to keep the same nature under environmental disturbances that smoothly change its phase and amplitude, thus suggesting a potential advantage for environment-resilient transfer of information.

However, in practice, typical disturbances may be strong enough to induce a transition in knot type, thus ruling out the potential of this approach. Here we show, through numerical and experimental investigation, how some types of optical knots recently realized experimentally; namely, Hopf link, trefoil, and cinquefoil, are robust under the action of phase distortions applied on the waist plane. The phase distortions are studied in terms of Zernike polynomials and of their relative strengths and defining apertures. Additional examples, like the superpositions of several aberrations and misalignment effects are considered. Lastly we also consider the simulations of distortions introduced in different propagation planes, an important step towards understanding the effects of turbulence on these structures

Results

Optical knots and links can all be generated by an optical field which in the plane z = 0 reads: $\psi (\rho ,\phi )=\exp (-{\rho }^{2}/(2{s}^{2}))\,{{\mbox{Poly}}}\,(\rho ,\exp (i\phi ))$, where (ρ, ϕ, z) are cylindrical coordinates, s is a width parameter specifying the size of a Gaussian envelope, and $\,{{\mbox{Poly}}}\,(\rho ,\exp (i\phi ))$ is a Milnor polynomial which specifies the knot type^22,23,24 (see Supplementary Note 1 for the explicit expressions).

Phase aberrations, which are the most common consequence of environmental disturbances and imperfections in optical setups, can be modeled as an additional phase factor δ(ρ, ϕ) applied on the undistorted field:

$$\widetilde{\psi }(\rho ,\phi )=\exp (i\delta (\rho ,\phi ))\psi (\rho ,\phi ).$$

(1)

Monochromatic optical aberrations can be expanded in Zernike functions:

$$\delta (\rho ,\phi )=\pi \mathop{\sum}\limits_{n,m}{\gamma }_{n,m}{Z}_{n}^{m}(\rho /A,\phi ),$$

(2)

where γ_n,m are real numbers which we call the strength of the (n, m)-th aberration, and ${Z}_{n}^{m}(\rho /A,\phi )={R}_{n}^{m}(\rho /A)\cos (m\phi )$ for positive m and ${Z}_{n}^{m}(\rho /A,\phi )={R}_{n}^{m}(\rho /A)\sin (m\phi )$ for negative n, with ${R}_{n}^{m}(\rho /A)$ the radial Zernike polynomial, defined in 0 ≤ ρ ≤ A. We recall that ∣m∣ ≤ n and $| {Z}_{n}^{m}(\rho /A,\phi )| \le 1$. Here, we mainly investigate the effect of the individual aberrations, up to 4-th order, on optical knots, thus applying phase distortions of the form,

$$\widetilde{\psi }(\rho ,\phi )={e}^{i\pi \gamma {Z}_{n}^{m}(\rho /A,\phi )}\psi (\rho ,\phi ).$$

(3)

In particular, we seek the critical values of the strengths γ and inverse aperture 1/A above which the knot topology is altered. It will be shown how knots can survive these aberrations for apertures slightly larger than the characteristic beam size and for strengths γ ≈ 1, which are much higher than values encountered in many practical scenarios. We then push towards smaller apertures to determine which aberrations can affect more the topological structure. It is found that aberrations like coma and secondary astigmatism are the most relevant. This is because these aberrations exhibit local maxima and minima in the interior of the aperture, thus introducing wavefront distortion in between the location of the phase singularities and affecting their trajectories.

The robustness of three different 3-dimensional optical topologies (Hopf link, Trefoil, and Cinquefoil) under various optical phase aberrations was experimentally investigated.

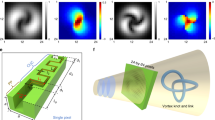
These structures were generated and detected with an approach similar to ref. ²¹. The principle of the experiment is shown in Fig. 1a, while details of the setup are reported in Method section: experimental setup. Optical knots can be obtained from computer-generated holograms displayed on a spatial light modulator (SLM). Exploiting the encoding introduced in ref. ²⁹, a phase mask is applied on an input Gaussian beam which is transformed in the desired knotted field after selecting the first diffraction order (this is done with a pinhole placed in the far field of the SLM). Aberrations effects can be introduced in a controlled way adding on the same SLM the aberration phase to the knot hologram. In this experiment, the knotted beam interferes collinearly with a reference Gaussian beam. On the translation stage, a CMOS camera is automatically translated to 75 different planes, recording interference patterns that are formed by changing the phase α of the reference beam. The reference phase is controlled using half of the SLM window (see refs. ^21,23 and experimental setup section). The phase of the structured beam in each plane can be reconstructed by means of phase-shifting digital holography. By tracking the phase singularities upon propagation, the singular skeleton was retrieved. Different aberrations, modeled as Zernike functions³⁰, were applied individually as additional phases with a specific aperture on the knot hologram.

Fig. 1: Experimental scheme and reconstructed aberrated knots.

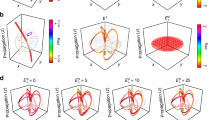
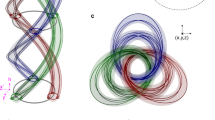
a Schematics of the experimental setup. An SLM displays a phase mask which encodes the knotted field and simultaneously applies the desired aberration mask (Eq. (1)). The desired field is obtained after a 4-f system and selection of the first diffraction order. The resulting field’s phase structure is reconstructed by phase-shifting digital holography, interfering with the knot field and a Gaussian reference beam. Recording the interference patterns at different propagation planes allows one to reconstruct the singular skeleton. b Examples of three-dimensional topologies affected by secondary astigmatism with γ = 1 experimentally reconstructed. From left to right: Hopf link, trefoil, and cinquefoil. The z-axis scale is, respectively, 74 cm, 39 cm, and 51 cm. The x and y axis scales are 0.25 cm. It should be noted that, for different topologies, a different second lens for the 4-f system was used to ensure the topology was confined within the range explored by the camera. The main plots show the experimentally observed singular skeletons and the phase patterns in different propagation planes. The reconstruction procedure of the singular skeleton from the phase patterns is detailed in the Methods. Insets show the top view of the singular skeleton (right) and the theoretical intensity patterns in the waist plane with red circles indicating the size of the aperture over which the Zernike polynomials were defined.

Robustness under the effect of individual aberrations

In agreement with simulations, it was observed that for each topology and aperture A higher than a critical value A_c, the structure survives all different aberrations with γ = 1. For each example, robustness up to at least γ = 1 was observed for values of A slightly larger than the characteristic beam intensity radius. Specifically, the topological structures were unaltered for aperture values A = 8w₀, 8w₀, and 4w₀ for Hopf link, trefoil, and cinquefoil, respectively, where w₀ is the characteristic waist parameter (which however, does not necessarily correspond to the beam size, the latter being also dependent on the parameter s). We point out that simulations predict that trefoil structures should survive high strength aberrations also for A = 7w₀, while experimentally, we observe a critical behavior for ${Z}_{4}^{2}$ (while other aberrations still give rise to trefoils). We attribute this mismatch to an additional phase perturbation present in the setup. Figure 1b shows examples of the three structures affected by secondary astigmatism (data for the other aberrations are given in Supplementary Note 3, Supplementary Fig. 1). The main effect of the aberrations is to stretch or compress the individual “lobes” of the curves leaving the overall topology unchanged. Therefore, if the aperture of the phase aberration compared to the beam waist w₀ is bigger than a critical value no aberrations (up to 4-th order) even with γ = 1 can break the topological structure. Beyond the 4th order, for the chosen maximum apertures, we theoretically observed breakups for some specific aberrations (e.g., ${Z}_{5}^{1}$ for trefoil—see Supplementary Note 3, Supplementary Fig. 2). This is not surprising, since, to a first approximation, these distortions resemble coma aberrations with higher strength.

Effects of smaller apertures

When decreasing A, knots and links can be broken into open trajectories. This effect can be, for instance, caused by singularity pairs created in the far field, which, instead of annihilating in back-propagation, join with the lines of the singular skeleton. For fixed γ = 1, we define the critical aperture (A_c) as the A in which the structure breaks up or cannot be fully reconstructed. The value of A_c is different for different aberrations typologies. For instance, in the case of the cinquefoil, A_c for ${Z}_{3}^{1}$, ${Z}_{4}^{0}$, and ${Z}_{4}^{2}$ is ≈ 3w₀ and for ${Z}_{2}^{0}$, ${Z}_{2}^{2}$, ${Z}_{3}^{3}$, and ${Z}_{4}^{4}$ is ≈2.3w₀. When A ≈ A_c, the effect of γ can be further investigated. In Fig. 2, experimental examples of links and knots under different aberrations with A ≈ A_c and γ < 1 are shown, highlighting how the topology can still be recovered for smaller strengths, even if is not preserved under the highest γ. We note that the experimental knots tend to break up for slightly higher apertures than theoretically expected. This is due to either experimental imperfections, which amount to additional aberrations perturbing the beam, or to residual interference with the zeroth order beam diffracted from the SLM. The latter case was analyzed in detail (see Methods Section: theoretical simulations) but may be less relevant in practical scenarios where aberrations are applied after the spatial filtering.

Fig. 2: Knot survival for small apertures.

The figure shows different singular skeletons obtained for aperture values slightly below the critical aperture A_c and for strengths γ < 1 such that the topology is conserved. The examples shown are for 3-rd and 4-th order aberrations, namely (a) trefoil, (b) quadrafoil, (c) coma, and (d) secondary astigmatism. The first column shows a three-dimensional plot of the aberrations with a texture given by the cinquefoil phase pattern to highlight how the different Zernike polynomials affect the wavefront near the phase singularities.

The topology of the singular skeleton can be more or less sensitive to different Zernike functions. The aberrations with stronger variations close to the singularities affect their evolution more and, therefore, can destroy the topology for larger A compared with aberrations responsible for distortions of the external parts of the wavefront. This is the reason why to coma (${Z}_{3}^{1}$) and secondary astigmatism (${Z}_{4}^{2}$) is associated a bigger A_c compared to trefoil (${Z}_{3}^{3}$) and quadrafoil (${Z}_{4}^{4}$) aberrations. As shown in the first column of Fig. 2, coma and secondary astigmatism have local minima and maxima in the interior of the defining circle, and so these variations can modify the wave vector distribution around the singularities, thereby altering their trajectory. On the other hand, distortions like ${Z}_{3}^{3}$ and ${Z}_{4}^{4}$, are mostly flat in their central region while being responsible for wavefront distortions close to the boundary of the defining circle. Hence, for large enough apertures, the phase singularities will lie in the central flat region, and the formation of the singular skeleton will be less affected.

Misalignment effects

Up to this point, we considered the case in which the defining aperture of the Zernike functions is perfectly centered with the unperturbed beam. However, lateral misalignments are a common source of imperfections. Hence, we looked into the effect of a relative displacement between the center of the beam and the center of the aberration’s defining circle. Figure 3 shows how displaced coma affects the cinquefoil knot. Relatively small displacements leave the singular skeleton topology unaltered, even for γ = 1. However, for the second displacement (Δx = 1.5w₀), it can be seen that ${Z}_{3}^{1}$ breaks the knot. We observed qualitatively similar effects for other aberrations (data are reported in Supplementary Note 3, Supplementary Fig. 3).

Fig. 3: Effect of aperture displacement.

The singular skeleton of a cinquefoil knot perturbed by a coma aberration with displaced origin (aperture A = 4w₀ and γ = 1). For displacement Δx = w₀ the knot topology is unaltered (a). For Δx = 1.5w₀ (b) the singular skeleton opens up due to joining with singularities created in the far field. Insets show the phase pattern in the waist plane (left) and the top view of the singular skeleton (right).

Isoplanar and multiplanar superpositions of aberrations

So far, we have considered high values of the strength by looking at the effect of individual aberrations. In practical scenarios, one deals with wavefront distortions described by a superposition of Zernike polynomials (as in Eq. (2)). As an example, we consider the effect of the wavefront distortion observed in a previous experiment on underwater high-dimensional quantum key distribution (ref. ³¹). The same distortion was applied to the cinquefoil beam, and, as shown in Fig. 4, the topology survives, which is not surprising since the γ_n,m are much smaller than 1. We point out that while this wavefront distortion is rather small, it was shown to have a significant effect on the security of orbital angular momentum (OAM)-based high-dimensional quantum key distribution. In particular, giving an error rate above the security threshold for dimensions higher than three³¹. This difference in robustness between OAM and knot-based encoding is strictly due to the topological nature of the singular skeletons of structured beams: on the one hand, optical aberrations can abruptly change the decomposition in a given spatial mode basis, thus affecting immediately the fidelity of the transmitted beam and the information encoded within its structure; on the other hand, the change in spatial mode decomposition induced by aberrations does not alter the topological structure associated with a knotted or linked beam, assuming that the strength and/or inverse defining aperture is below a given threshold. Thus, the survival of knot fields under relevant wavefront distortion is a promising example of how these structures can provide a more robust way to encode information. However, we stress that deeper studies on the effects of turbulence must be carried out to certify this advantage. For instance, turbulent channels are better modeled by considering that phase distortions are not introduced in a single plane. One can ask if a knot field propagating through several random phase masks can still keep its topology unaltered. We carried a few simulations of this kind for some examples in which we considered the propagations through multiple, equally spaced phase masks. The masks were obtained as superpositions of Zernike polynomials with coefficients extracted from a Gaussian distribution with zero mean and standard deviation calculated based on ref. ³². In our simulations we chose typical values of the Fried parameter r₀ = 180, 10 mm and the spacing between the planes Δz = r₀. The field was numerically propagated over a range of 2 × 75 cm (corresponding to twice the focal length f₁ = f₂ of the lenses shown in Fig. 5). In these configurations, we observed the survival of cinquefoil knots. This is somewhat not surprising since the individual phase masks introduce relatively weak phase distortions. We thus expect that moderate levels of turbulence, which can be compensated by an adaptive optics system, will not present a serious obstacle to the transmission of either classical or quantum information by means of three-dimensional optical topological structures. We also considered two other cases simulating a generic system with multiple wavefront-distortion-inducing slabs (not related to turbulence models): first the variance of the normal distribution (with zero mean) of the coefficients was increased to 1, second we considered random strengths uniformly distributed between 0 and 1 for the first nine Zernike polynomials. We observed a full knot with ten aberration masks for both of these cases.

Fig. 4: Cinquefoil knot subject to a superposition of aberrations.

a Plot of the wavefront distortion applied to a cinquefoil knot. The distortion was obtained from a superposition of Zernike polynomial reported in ref. ³¹. b Side view and top view (inset) of the reconstructed singular skeleton which dysplays a cinquefoil topology.

Fig. 5: Knot propagation through multiple phase masks.

a Schematics of the simulated process. A knotted field is generated by a spatial light modulator (SLM)—the imaging system selecting the first diffraction order is omitted for simplicity—and sent through a free space channel with equally spaced phase masks. The distorted field is then captured by a second lens and reconstructed. The performed simulations, based on Zernike polynomial decomposition of Kolmogorov turbulence models (see text), show robustness for typical values of turbulence. b, c These show side and top views of a simulated cinquefoil knot propagated through 150 phase planes obtained as superposition of the first 54 Zernike polynomials (up to n = 10) with random coefficients extracted from a Gaussian distribution with width given by ref. ³², assuming r₀ = 10 mm, R = 4w₀.

Conclusions

In conclusion, we have demonstrated experimentally how simple optical knots and links are robust under phase aberrations and setup misalignments, thus hinting at their potential advantage in communication protocols. Moreover, we showed how the aberrations exhibiting local minima or maxima in the interior of the circle defining the Zernike polynomials are those which can more significantly affect the topology of the singular skeleton. These considerations can be useful not only for communication purposes but also in devising setups to generate knotted fields in more delicate scenarios, e.g., in nanophotonics experiments¹⁰ or in setups for other kinds of structured quantum waves^33,34, e.g., electrons and neutrons³⁵. We also note that results in the nonlinear regime can be expected to be completely different. Effects such as self-focusing may cause singularity crossing and thus the transition to trivial line singularities.

In this work, we have shown that these structures can be altered without affecting their topology, and thus the encoded information, when propagating in media that introduce relatively strong aberrations. However, other challenges need attention, starting with the practical implementation of higher-order structures, and a fast and reliable reconstruction. The first challenge can be faced by the nested knot approach²⁴, which allows to scale the prime number encoding by accessing multiple wavelengths. The second challenge can be addressed by introducing single or few-plane knot detection based either on the post-processed digital propagation of the detected amplitude and phase or on phase retrieval from multiple-plane intensity detection.

Methods

Experimental setup

In Fig. 6, we report a more detailed experimental setup. An 808 nm diode laser is coupled to a single-mode fiber, and a Gaussian profile for the beam is generated, which is then sent to a folded-Sagnac interferometer with a Polarising Beam Splitter (PBS) as the input/output port. The vertically polarized beam is converted to a horizontally polarized one by a half-wave plate before reaching the right side of a liquid crystal Spatial Light Modulator (SLM). The SLM replaces the intermediate mirror of the interferometer and displays two holograms on each side, hence applying different transformations on the two beams. On the left side, the knot-generating hologram is applied, while the right side only shifts the phase of the incident beam. Both hologram functions are also superimposed with a blazed grating so that the modulated light is deflected to the first diffraction order. The reference beam is converted to vertical polarization by the same waveplate that acted on the knot hologram’s input. In this way, the two beams will both exit the input port of the PBS. The interferometer is aligned to avoid overlap with the input beam and to ensure perfect collinearity of the two output beams. A pinhole placed in the center of the 4-f system selects the first diffraction order of the SLM. The pinhole aperture and diffraction angle were different depending on the implemented structured beam to minimize the interference with the zeroth order and, at the same time, avoid cutting weak radial contributions necessary for the formation of the desired topology. After the 4-f system the field is $\tilde{\psi }(\rho ,\phi ,z){{{{{{{{\bf{e}}}}}}}}}_{H}+{e}^{i\alpha }{\psi }_{{{\mbox{ref}}}}(\rho ,z){{{{{{{{\bf{e}}}}}}}}}_{V}$ with α = 0, π/2, π, 3π/2, $\tilde{\psi }(\rho ,\phi ,z)$ the aberrated knot, ψ_ref(ρ, z) the reference Gaussian beam. Projecting on a diagonal polarization (with a half-wave plate and a PBS) we obtained a scalar superposition between the structured beam and the reference. A CMOS camera placed on a motorized translation stage was used to record the intensity patterns of the resulting superposition for different relative phases, thus allowing for phase reconstruction based on phase-shifting digital holography (see Supplementary Note 2).

Fig. 6: Experimental setup.

SLM Spatial Light Modulator, M Mirror, HWP Half Wave-Plate, PBS Polarising Beam-Splitter, L Lens, HM D-Shaped Mirror, Ph Pinhole.

Theoretical simulations

To explore the wide parameter space and choose which case to look for experimentally, we simulated the propagation of the aberrated knotted fields using a Fresnel Transfer Function propagator. We define each field over a 2048 × 2048 array and a simulation window with a half-length of 24w₀, where w₀ is the simulated beam’s dimensionless waist parameter, and a numerical wavelength of 0.0134w₀. We compute the propagation of the knotted beam given at z = 0 within the range z = ±z₀, where ${z}_{0}=\pi {w}_{0}^{2}/\lambda$ refers to the Rayleigh range.

Our experimental results, in some cases, show breakup also in situations where simulations predict the survival of the topological structure. Some discrepancies can be partially explained when considering interference from the zeroth diffraction order of the SLM, which, when applying stronger aberrations, can exhibit a small overlap with the first order. We thus compared the simulations in the ideal case with simulations considering the hologram implementation used in our experiment. We generate a hologram encoding the aberrated knotted field, using the scheme proposed by ref. ²⁹. The SLM acts as a phase mask applied onto a Gaussian beam with a large waist (relative to the knotted beam) of 10w₀. To simulate the effect of the pinhole placed in the far field of the diffracted beam, we applied a Fourier filter encoded as a Heaviside function θ(1 − f_r/σ), where ${f}_{r}^{2}={f}_{x}^{2}+{f}_{y}^{2}$ is the radial component in Fourier space and σ is the pinhole aperture. The value of σ was determined experimentally by imaging the iris aperture when illuminated with a Gaussian beam set with waist w₀ on the SLM plane.

Fig.7 illustrates an example which demonstrates the effect of simulating the interference of the zeroth order onto the theoretical simulations. When subjected to this aberration at the highest strength and with A = 7w₀, the trefoil knot is not observed to survive in the experiment (Fig. 7c) due to one branch of the singular skeleton opening up. Simulations at A = 7w₀ predict, with and without SLM effects included, the existence of the trefoil structure, but with additional singularity lines approaching the knot. Decreasing the value of A to 6.6w₀ we indeed observe that, if the zeroth diffraction order is taken into account, the knot breaks up as observed in the experiment (Fig. 7b) while it does not in ideal conditions (Fig. 7a). The reason we observe a residual discrepancy in the aperture values must be attributed to additional imperfections in the setup, e.g., deformations of the SLM window itself and imperfect centering of the hologram.

Fig. 7: Simulating the effects of diffraction from the SLM.

We show the simulation of a trefoil knot affected by secondary astigmatism for aperture A = 6.6w₀ without (a) and with (b) the effects of the zeroth diffraction order included. These results partially explain the breakup observed at A = 7w₀ in the experiment (c).