Introduction

Over the past decade, it has been shown that continuous wave-driven Kerr nonlinear resonators host a variety of coherent dissipative structures1,2. In the anomalous dispersion regime, they give rise to dissipative Kerr solitons (DKS)3, while in the normal dispersion regime, platicons4,5, or interlocked switching waves, have been generated. These coherent dissipative structures give rise to a wide range of nonlinear dynamical phenomena, ranging from breathers6,7 and soliton switching8 to chaotic behavior9. Mathematically, in leading order, the dynamics can be described by the 1D driven-dissipative nonlinear Schrödinger equation (NLSE)10 known as the Lugiato-Lefever equation (LLE)11,12, and extension thereof, e.g., to include multi-mode dynamics or the Raman nonlinearity13. In this framework, a variety of nonlinear phenomena have been observed4,5,14,15,16,17,18. On the application side, in particular, the DKS formation process has been utilized and has enabled photonic integrated microresonator-based optical frequency comb generation with applications ranging from coherent communications19 and neuromorphic computing20 to atomic clocks21.

Yet to date, almost all experimental and theoretical works on ‘dissipative structures’ in optically driven Kerr nonlinear resonators (be it fiber22,23 or microresonator based) have focused on the single resonator case, and only recently extended to the dimer case24,25,26. The recent advances in ultra-low loss nonlinear integrated platforms, particularly silicon nitride27,28, have dramatically reduced the threshold for optical parametric oscillations and concomitant dissipative structure generation — at and below the milliwatt level. This indicates that large-scale arrays of coupled Kerr nonlinear resonators that combine spatial and synthetic frequency dimensions29 are within experimental reach — yet their nonlinear dynamics under continuous-wave driving remain largely unexplored, both theoretically and experimentally. Such systems are expected to exhibit rich nonlinear dynamics and novel 2D dissipative structures that have combined spatial and temporal dimensions. Even the simple case of a photonic dimer has demonstrated a variety of emergent nonlinear dynamics24,25 and phenomena such as soliton hopping and recurrent dispersive waves. 1D and 2D lattices are particularly attractive as they allow significantly more complex dispersion landscapes — opening ways to engineer dispersion beyond the traditional approaches. Therefore, chains of resonators are expected to provide a pathway to octave-spanning DKS30, which is an enduring outstanding challenge in the field. Such spectra are required for the self-referencing of micro-combs31. Lattices of nonlinear resonators also allow studying topological systems (e.g., the Su-Schrieffer-Heeger (SSH) model or honeycomb lattices32,33), which over the past decade have been extensively studied in the linear regime in photonics. Nonlinear effects, and spatial solitons in particular, have already been observed and studied in arrays of coupled optical waveguides34,35,36. Crucially these nonlinear effects however did not include parametric frequency conversion (i.e., parametric oscillations), which is the underlying physical principle for soliton microcombs. However, a first analysis of DKS formation was carried out in37, where the authors studied Kerr nonlinear version of the photonic 2D Haldane model made of coupled multi-mode optical microresonators with anomalous dispersion that are coupled via link resonators.

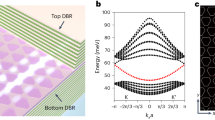
In this manuscript, we analyze dissipative structures in optically driven coupled chains of nonlinear resonators in the absence and presence of the edge modes. First, we provide a general description of nonlinear dynamics in an arbitrary N-dimensional lattice of resonators and derive an effective (N+1)D coupled-mode equation (Fig. 1a, b). Next, we study the 1D chain of equally coupled resonators (see Fig. 1a), providing a leading order model in the form of the 2D continuous-discrete LLE. This model demonstrates a net difference in comparison with its lower dimensional counterpart. In particular, we observe fundamentally distinct nonlinear regimes attributed to the local dispersion profile: elliptic and hyperbolic. Investigating Turing patterns and chaotic states in this system, we observe a drastic difference between the considered regimes that emerge due to the four-wave mixing (FWM) pathways structure mimicking the gain lobes profiles. Performing dynamical simulations, we show the effect of regularized wave collapses and the emergence of solitons that are inherently two-dimensional spatiotemporal mode-locked structures. Furthermore, we study a dimerized chain of coupled resonators described by the simplest topological model, the SSH model (Fig. 1c). We focus on the aspect of DKS generation in the edge state that is localized in the middle of the photonic bandgap. Specifically, we show that edge-state solitons, in the absence of interactions with the bulk, can be approximated by the conventional single-resonator DKS (Fig. 1d). However, for the experimentally accessible set of parameters, the generated DKS in the edge states can induce edge-to-bulk scattering and generation of the dispersive waves that can strongly disturb soliton coherence and shorten its existence range.

Fig. 1: Dispersion hybridization in lattices of resonators.
figure 1

a Chain of equally coupled resonators. Dispersion of the spatial supermodes results in a two-dimensional hybridized surface. Blue asterisks represent the cosine band structure of a single mode for which integrated supermode dispersion at k = 4 is presented in panel (b). b Integrated supermode dispersion of the edge state of the Haldane model compared to the dispersion of a chain of resonators. Inset: numerically computed band structure for 21 × 21 resonators with phase flux in the unit cell π. c Schematics of the Su-Schrieffer-Heeger model and its dispersion for a ten resonator chain. Each resonator mode from panel (d) hybridizes accordingly with the band structure, forming a total hybridized dispersion profile with the bulk (green dots) and the edge parabolas. Here the red line schematically represents the edge state DKS. d Schematics of a single Kerr microresonator and its chromatic dispersion. The red line represents the dissipative Kerr soliton (DKS).

Full size image

In this manuscript, we derive an effective (N+1)D coupled-mode equation for the general case of nonlinear dynamics in an arbitrary N-dimensional lattice of resonators (Fig. 1a, b), following by a detailed study of a 1D chain of equally coupled resonators. We demonstrate that this systems has a 2D dispersion surface that defines two fundamentally distinct nonlinear regimes: elliptic and hyperbolic. In these regimes, we numerically investigate stable and chaotic dynamics. For the former, we study coherent dissipative structures, such as Turing patterns and 2D DKS that correspond to spatio-temporal mode-locking of the optical modes in different resonators. In the latter, we compare the chaos in both dynamical regimes and attribute the observed difference to the presence of the regularized wave collapse in the elliptic regime. We conclude by considering DKS generation in the edge state of the SSH model (Fig. 1c). We demonstrate nonlinearly induced edge-to-bulk scattering and generation of the dispersive waves that can strongly disturb soliton coherence and shorten its existence range, which can be deduced from single resonator approximation (Fig. 1d).

Results

Coupled Lugiato-Lefever equations in lattices of resonators

We start with a general description of a system of weakly coupled (coupling rate ≪ free spectral range (FSR)) identical optical resonators that is shown to be governed by a set of linearly coupled LLEs, which can be presented in matrix form as

$$\frac{\partial }{\partial t}{\mathbb{A}}=\hat{{\mathbb{D}}}{\mathbb{A}}+i\hat{{\mathbb{M}}}{\mathbb{A}}+i{g}_{0}| {\mathbb{A}}{| }^{2}{\mathbb{A}}+{\mathbb{F}},$$
(1)

where vector \({\mathbb{A}}={[{A}_{0},...,{A}_{N-1}]}^{T}\) contains optical field envelopes of each resonator as a function of the azimuthal angle in the co-moving frame φ in the lattice, matrix

$$\begin{array}{l}\hat{{\mathbb{D}}}={{{{{{{\rm{diag}}}}}}}}\left[-\left(\frac{{\kappa }_{0}+{\kappa }_{{{{{{{{\rm{ex}}}}}}}},0}}{2}+i\delta {\omega }_{0}\right)+i\frac{{D}_{2}}{2}\frac{{\partial }^{2}}{\partial {\varphi }^{2}}\right.,...,\\ ...,-\left.\left(\frac{{\kappa }_{0}+{\kappa }_{{{{{{{{\rm{ex}}}}}}}},N-1}}{2}+i\delta {\omega }_{0}\right)+i\frac{{D}_{2}}{2}\frac{{\partial }^{2}}{\partial {\varphi }^{2}}\right]\end{array}$$

contains detuning (δω0), losses (κ0), dispersion of each resonator (D2), and coupling to the bus waveguides (κex,ℓ). The coupling between different rings is introduced in matrix \(\hat{{\mathbb{M}}}\), the nonlinear term \(| {\mathbb{A}}{| }^{2}{\mathbb{A}}={[| {A}_{0}{| }^{2}{A}_{0},...,| {A}_{N-1}{| }^{2}{A}_{N-1}]}^{T}\) describes the conventional Kerr nonlinearity with single photon Kerr frequency shift g0, and \({\mathbb{F}}={[\sqrt{{\kappa }_{{{{{{{{\rm{ex}}}}}}}},0}}{s}_{{{{{{{{\rm{in}}}}}}}},0},...,\sqrt{{\kappa }_{{{{{{{{\rm{ex}}}}}}}},N-1}}{s}_{{{{{{{{\rm{ex}}}}}}}},N-1}]}^{T}\) represents the pump. Usually, the coupling matrix \(\hat{{\mathbb{M}}}\) is diagonalizable and possesses a set of eigenvectors \(\{{{\mathbb{V}}}_{i}\}\) and associated eigenvalues λi, so any state \({\mathbb{A}}\) can be represented on this basis as

$${\mathbb{A}}=\mathop{\sum}\limits_{j}{c}_{j}{{\mathbb{V}}}_{j},$$
(2)

where coefficients \({c}_{j}=\langle {\mathbb{A}}| {{\mathbb{V}}}_{j}\rangle\) correspond to the amplitude of the supermode \({{\mathbb{V}}}_{j}\) and 〈 ⋅ ∣ ⋅ 〉 indicates the scalar product. Therefore, Eq. (1) can be rewritten for the amplitudes cj in the basis of eigenvectors \(\{{{\mathbb{V}}}_{j}\}\), where the linear part of the equation will take a form of a matrix with eigenvalues λj on the diagonals corresponding to the resonance frequencies of the collective excitations. However, the nonlinear term will no longer be diagonal on this basis. In the direct space, the nonlinear term takes form

$$| {\mathbb{A}}{| }^{2}{\mathbb{A}}=\mathop{\sum}\limits_{{j}_{1},{j}_{2},{j}_{3}}{c}_{{j}_{1}}{c}_{{j}_{2}}{c}_{{j}_{3}}^{* }{{\mathbb{V}}}_{{j}_{1}}{{\mathbb{V}}}_{{j}_{2}}{{\mathbb{V}}}_{{j}_{3}}^{* }.$$

Projecting this expression onto the state \({{\mathbb{V}}}_{j}\), one obtains the coupled-mode equations for the amplitudes cj

$$\frac{\partial {c}_{j}}{\partial t}= -\left(\frac{{\kappa }_{0}+{\kappa }_{{{{{{{{\rm{ex}}}}}}}}}}{2}+i\left(\delta {\omega }_{0}-{\lambda }_{j}\right)\right){c}_{j}+i\frac{{D}_{2}}{2}\frac{{\partial }^{2}{c}_{j}}{\partial {\varphi }^{2}} \\ +i{g}_{0}\mathop{\sum}\limits_{{j}_{1},{j}_{2},{j}_{3}}{c}_{{j}_{1}}{c}_{{j}_{2}}{c}_{{j}_{3}}^{* }\left\langle {{\mathbb{V}}}_{{j}_{1}}{{\mathbb{V}}}_{{j}_{2}}{{\mathbb{V}}}_{{j}_{3}}^{* }| {{\mathbb{V}}}_{j}\right\rangle +{\tilde{f}}_{j},$$
(3)

where \({\tilde{f}}_{j}=\langle {\mathbb{F}}| {{\mathbb{V}}}_{j}\rangle\) is the projection of the pump on the eigenstate \({{\mathbb{V}}}_{j}\), the nonlinear term represents the conventional FWM process with the conservation law dictated by the product \(\langle {{\mathbb{V}}}_{{j}_{1}}{{\mathbb{V}}}_{{j}_{2}}{{\mathbb{V}}}_{{j}_{3}}^{* }| {{\mathbb{V}}}_{j}\rangle\). The eigenvalues λj, showing the dependence of supermode frequency on supermode number, naturally start to play a role of dispersion, similar to the conventional LLE in a single resonator. In general, the eigenvalues λj are not equidistantly separated, and the supermode dispersion can be introduced similar to the integrated dispersion of a single resonator \({D}_{{{{{{{{\rm{int}}}}}}}}}(k)={\lambda }_{k}-{\lambda }_{{k}_{0}}-{J}_{1}(k-{k}_{0})\), where J1 is the local FSR of the spatial supermodes in the vicinity of k0. Depending on the system, the supermode dispersion has the same dimensionality \({{{{{{{\mathcal{D}}}}}}}}\) as the system’s band structure. Thus, the total hybridized dispersion (including the chromatic dispersion) profile for photons in the system has \({{{{{{{\mathcal{D}}}}}}}}+1\) dimensionality.

We note, however, that the key requirement for the validity of the reasoning presented above is the diagonalizability of the coupling matrix \({\mathbb{M}}\) which does not impose any restriction on the dimensionality of the system.

Chains of coupled microresonators

Two-dimensional hybridized dispersion

We continue our analysis by considering a system of the equally coupled chain of resonators. First, we explicitly write Eq. (1) in the case of constant coupling in a chain

$$\frac{\partial {A}_{\ell }}{\partial t}= -\left(\frac{{\kappa }_{{{{{{{{\rm{ex}}}}}}}},\ell }+{\kappa }_{0}}{2}+i\delta {\omega }_{0}\right){A}_{\ell }+iJ\left({A}_{\ell -1}+{A}_{\ell +1}\right)\\ +i\frac{{D}_{2}}{2}\frac{{\partial }^{2}{A}_{\ell }}{\partial {\varphi }^{2}}+i{g}_{0}| {A}_{\ell }{| }^{2}{A}_{\ell }+\sqrt{{\kappa }_{{{{{{{{\rm{ex}}}}}}}},\ell }}{s}_{{{{{{{{\rm{in}}}}}}}},\ell }{e}^{i{\phi }_{\ell }}.$$
(4)

For simplicity, in the case of constant couplings to the bus waveguides κex,ℓ, we introduce normalized variables d2 = D2/κ, κ = κ0 + κex, ζ0 = 2δω/κ, j = 2J/κ, \({f}_{\ell }=\sqrt{8{\kappa }_{{{{{{{{\rm{ex}}}}}}}}}{g}_{0}/{\kappa }^{3}}{s}_{{{{{{{{\rm{in}}}}}}}},\ell }{e}^{i{\phi }_{\ell }}\), \({\Psi }_{\ell }=\sqrt{2{g}_{0}/\kappa }{A}_{\ell }\). In the normalized units, Eq. (4) reads

$$\frac{\partial {\Psi }_{\ell }}{\partial \tau }= -\left(1+i{\zeta }_{0}\right){\Psi }_{\ell }+i{d}_{2}\frac{{\partial }^{2}{\Psi }_{\ell }}{\partial {\varphi }^{2}}+ij\left({\Psi }_{\ell -1}+{\Psi }_{\ell +1}\right)\\ +i| {\Psi }_{\ell }{| }^{2}{\Psi }_{\ell }+{f}_{\ell }.$$
(5)

Further, we can readily diagonalize the linear part by taking the Fourier transform

$${\psi }_{\mu k}=\frac{1}{2\pi \sqrt{N}}\int\mathop{\sum }\limits_{\ell =1}^{N}{\Psi }_{\ell }{e}^{2\pi i(\ell k/N+\mu \varphi )}d\varphi ,$$
(6)

where k is the supermode index and μ is the comb line index. With the Kerr term, Eq. (5) transforms to

$$\frac{\partial {\psi }_{\mu k}}{\partial \tau }= -(1+i{\zeta }_{0}){\psi }_{\mu k}-i\left[{d}_{2}{\mu }^{2}-2j\cos \frac{2\pi k}{N}\right]{\psi }_{\mu k}+{\delta }_{\mu 0}{\tilde{f}}_{k} \\ +\frac{i}{N}\mathop{\sum}\limits_{\begin{array}{c}{k}_{1},{k}_{2},{k}_{3}\\ {\mu }_{1}{\mu }_{2}{\mu }_{3}\end{array}}{\psi }_{{\mu }_{1}{k}_{1}}{\psi }_{{\mu }_{2}{k}_{2}}{\psi }_{{\mu }_{3}{k}_{3}}^{* }{\delta }_{{\mu }_{1}+{\mu }_{2}-{\mu }_{3}-\mu }{\delta }_{{k}_{1}+{k}_{2}-{k}_{3}-k}.$$
(7)

In this form, we obtain the analytical expression for the hybridized 2D dispersion surface

$${d}_{{{{{{{{\rm{int}}}}}}}}}(\mu ,k)=2({\omega }_{\mu k}-{\omega }_{0}+{D}_{1}\mu )/\kappa ={d}_{2}{\mu }^{2}-2j\cos (2\pi k/N).$$
(8)

In the case of anomalous group velocity dispersion (GVD) (d2 > 0, Fig. 1d) of the individual resonator, this surface with parabolic and cosine cross-sections is shown in Fig. 1a. Local dispersion topography changes along the k axis, revealing different regions with parabolic and saddle shapes. The pump term \({\tilde{f}}_{k}\) stands for the projection of the pump on the k-th supermode

$${\tilde{f}}_{k}=\frac{1}{\sqrt{N}}\mathop{\sum }\limits_{\ell =1}^{N}{f}_{\ell }{e}^{2\pi i\ell k/N}.$$
(9)

Spatial eigenstates and pump projection on the chain

The supermode dispersion (i.e., band structure) has regions of anomalous and normal supermode group velocity dispersion (sGVD). For a given supermode index k0, the linear term in the Taylor series of the cosine gives the supermode FSR equal to \({J}_{1}/2\pi =2J/N\sin (2\pi {k}_{0}/N)\) and the corresponding quadratic term yields sGVD \({J}_{2}=2J{(2\pi /N)}^{2}\cos (2\pi {k}_{0}/N)\) for eq. (4).

The excitation of the individual supermode requires an accurate pump projection on its spatial profile. In case of imperfect projection of the pump, the number of the excited modes will depend on the local density of states within the width of the band. Moreover, the single-resonator pump scheme always leads to the excitation of supermodes in pairs due to their two-fold degeneracy, except for the modes from the very top and bottom of the band. According to Eq. (9), if the resonator ℓ = 0 is pumped, all the supermodes have a pump term with the projection amplitude \(1/\sqrt{N}\). With the increasing number of resonators, a pumping scheme with a single resonator excitation becomes less efficient, and more sophisticated schemes are required. For simplicity of the further analysis, in the following we focus on the ideal case of a single supermode excitation. Accurate projection to the supermode with index k0 requires accurate adjustment the relative phases of the pump lasers according to

$${{{{{{{\bf{f}}}}}}}}={f}^{(0)}\left[1,{e}^{-2\pi i{k}_{0}/N},{e}^{-4\pi i{k}_{0}/N},...,{e}^{-2(N-1)\pi i{k}_{0}/N}\right],$$
(10)

where \({f}^{(0)}=\sqrt{8{g}_{0}{\kappa }_{{{{{{{{\rm{ex}}}}}}}}}P/{\kappa }^{3}\hslash \omega N}\) is normalized pump for a single resonator.

Modulation instability gain lobes

Further, we investigate the stability of plane wave solutions ψ00. Considering the pump at μ0 = 0 and at the parabolic region k0 = 0 (saddle point k0 = N/2), we investigate FWM processes between the pump mode and the modes with indexes μ, k. Linearizing the system, we identify the modes with positive parametric gain. Our analysis, similar to38, shows that the modulationally unstable solutions form an ellipse (hyperbola) in the μ − k space (k ≠ 0, μ ≠ 0).

$${d}_{2}{\mu }^{2}\pm {j}_{2}{k}^{2}=4| {\psi }_{00}{| }^{4}+\sqrt{| {\psi }_{00}{| }^{4}-1}-({\zeta }_{0}\mp 2j),$$
(11)

here + ( − ) stands for the excitation of k − k0 = 0 (k − k0 = N/2). An example of the modulation instability (MI) gain lobes [Eq. (11)] is presented in Fig. 2a, b for both regions in case of d2 = 0.04 and j2 = ∣J2∣/κ = 1. Figure 2a reveals that the supermode corresponding to the excitation of all the resonators in-phase (anomalous sGVD) is unstable against small perturbations with μ and k indexes that form an ellipse. The width and height of the ellipse are defined by pump power, d2, and j2 coefficients that correspond to GVD and sGVD. In contrast, the state corresponding to the excitation of the neighboring resonators in the opposite phase (normal sGVD) is unstable against the perturbations with μ and k forming a hyperbola (see Fig. 2b), showing that all the supermodes can experience positive parametric gain.

Fig. 2: Modulation instability gain lobes in chains of coupled resonators.
figure 2

Hybridized dispersion profile shown as a surface in panel (a) for the elliptic and (b) for the hyperbolic regions. Contour plots in the k − μ plane at Dint = 0 highlight the different local topographies that result in the elliptic (a) or hyperbolic (b) modulation instability gain lobes depicted in red.

Full size image

Wave collapse

We continue with the simulation of the coupled LLEs in Eq. (4) for 20 resonator chain and constant normalized coupling j = 10 (j2 = 1). To simulate the temporal dynamics, we employ the step-adaptative Dormand-Prince Runge-Kutta method of Order 8(5,3)39 and approximate the dispersion operator by the second-order finite difference scheme. We deliberately choose the pumping scheme allowing for exciting only a given mode. To trigger the FWM processes, we numerically scan the resonance with a fixed pump power and track field dynamics in all the resonators.

First, we focus on the investigation of the unstable behavior of the system pumping the elliptic (k0 = 0) and hyperbolic regions (k0 = N/2) with the pump fℓ = 2.35 and corresponding detunings ζ0 = 22.1 and ζ0 = −17.0. In the former case, at a single resonator level we observe the random appearance of the pulses in different parts of the cavity and further their rapid compression, during which the peak amplitude significantly exceeds (60 times) the background level (cf. Fig. 3a). Computing the nonlinear dispersion relation (NDR)24,40, we observe the high photon occupancy of the pump region beneath the parabolas (cf. Fig. 3b), which indicates the presence of 2D dissipative nonlinear structures. Furthermore, all the hybridized parabolas are populated by the photons, meaning that supermodes from both dispersion regions are excited (please also refer to the Supplementary Movie 1 demonstrating resolved dynamics in time of the field in all resonators and the corresponding 2D k − μ spectrum). To further confirm it, we reconstruct the supermode NDR (sNDR) for the 0th comb line (μ0 = 0) for all resonators in the following way

$${{{{{{{\rm{sNDR}}}}}}}}(\Omega ,{\mu }_{0},k)=\frac{1}{\sqrt{{N}_{t}N}}\mathop{\sum}\limits_{\ell ,n}{\psi }_{{\mu }_{0}\ell }(t){e}^{i(2\pi k\ell /N-\Omega {t}_{n})},$$
(12)

where Ω is slow frequency, tn = Δtn with Δt = T/Nt time-step, T is simulation time with Nt number of discretization points. The result is shown in Fig. 3c. The whole cosine band structure is populated, including the region of the normal dispersion. In the opposite case, the spatiotemporal diagram (Fig. 3d) in hyperbolic region does not demonstrate any extreme events, showing slow (with respect to the elliptic case) incoherent dynamics (cf. Supplementary Movie 2). Comparing the NDR (Fig. 3e) with the elliptic case, we show less supermode occupancy. In the vicinity of μ = 0, the normal sGVD suppresses the photon transfer along the k axis. Nevertheless, the photon transfer to other supermodes is stimulated with respect to eq. (11) that depicts MI gain lobes position, resulting in the generation of dispersive waves24,25. Reconstructing the supermode NDR (Fig. 3f) for μ = 25 comb line [the average crossing position in Fig. 3e], we observe the predominant population of the center of the band.

Fig. 3: Numerical reconstruction of the nonlinear dispersion relation in the elliptic and hyperbolic regions in the unstable regime.
figure 3

Panels (a–c) correspond to the elliptic region (k0 = 0, d2 > 0, j2 > 0), panels (d–f) to the hyperbolic (k0 = N/2, d2 > 0, j2 < 0). Spatiotemporal diagrams of unstable states in 0th resonator are shown in (a) and (d); The corresponding nonlinear dispersion relation (NDR) in the elliptic region (b) demonstrates excitation of all the optical and spatial modes, whereas the NDR in the hyperbolic region (e) reveals that photon transfer between the spatial supermodes is suppressed in the vicinity of the pump mode μ = 0; The panels (c) and (f) represent the nonlinear supermode dispersion relation [Eq. (12)] of 0th comb line for the state in (a) and 25th comb line for the state in (d).

Full size image

We attribute this drastic difference in the chaotic dynamics to the effect called wave collapse41,42 that plays an important role in physics and leads to an effective mechanism of local energy dissipation. Our system, in the long-wavelength limit, can be modeled by 2D LLE with elliptic (\({\partial }_{\varphi \varphi }^{2}+{\partial }_{\theta \theta }^{2}\)) or hyperbolic (\({\partial }_{\varphi \varphi }^{2}-{\partial }_{\theta \theta }^{2}\)) dispersion (here θ stands for the continuous coordinate along the circumference of the chain). Neglecting the pump and damping terms, we obtain the conservative 2D NLSE, which in the elliptic case can result in full compression of a pulse to an infinitely small area concentrating there a finite amount of energy43,44. Such pulse becomes ultra-broad in the spectral domain, and even the presence of dissipation in 2D LLE does not restrict this effect45. On the contrary, wave collapses do not occur in the 2D focusing NLSE with hyperbolic dispersion44, signifying that it is the dispersion curvature that is responsible for the effect. Moreover, higher dispersion orders of the cosine limit the pulse compression in the elliptic region, regularizing the singularity46.

Coherent dissipative structures (Turing patterns and 2D dissipative solitons)

Turing patterns. As the different dispersion topographies result in completely different chaotic dynamics, the Turing patterns in the elliptic and hyperbolic regions differ in the same way. To observe the coherent structures, we first bring the system to into an unstable state. Stimulating the incoherent patterns, we further tune towards the monostable region (\({\zeta }_{0}^{{k}_{0}}={\zeta }_{0}\mp 2j < \sqrt{3}\), + ( − ) stands for k0 = 0 (N/2)), pass through breathers (e.g., Supplementary Movie 3 indicating distorted breathing Turing pattern in the elliptic regime), and obtain stable coherent structures in both regimes (Fig. 4). One can see that in the elliptic regime at ∣fℓ∣ = 1.05 and ζ0 = 20.5, we observe the formation of a Turing pattern (Fig. 4a)47,48,49. On a single resonator level, this corresponds to locked pulses (Fig. 4b) with a typical comb spectrum shown in Fig. 4d. The corresponding 2D k-μ spectral profile in Fig. 4c shows that the sidebands form a disk, occupying the supermodes from both anomalous (∣k − k0∣ < 5) and normal dispersion regimes. In the hyperbolic regime, at ∣fℓ∣ = 2.35 and ζ0 = −20.3, we observe a train of pulses in each resonator locked to each other (Fig. 4e, f). The corresponding 2D spectral profile (Fig. 4g) forms a line in k-μ space, that qualitatively follows one of the asymptotes of the hyperbola that depicts modulation instability gain lobes in Fig. 2b (also similar to50). Comparing the comb spectra at the 1st resonator (Fig. 4d) with the elliptic case (Fig. 4h), one can notice that the state at the hyperbolic regime has a wider comb spectrum.

Fig. 4: Coherent dissipative structures in a driven nonlinear photonic ring lattice.
figure 4

Panels (a–d) correspond to the elliptic region (k0 = 0, d2 > 0, j2 > 0), and panels (e–h) correspond to the hyperbolic (k0 = N/2, d2 > 0, j2 < 0). Spatiotemporal profiles of the mode-locked structures are shown in panels (a, e) with the corresponding field profile on a single resonator level in panels (b, f). The 2D spectral profiles of the states (a) and (e) obtained via Eq. (6) are presented in (c) and (g), respectively. The spectral profile in elliptic regime (c) forms a disk, whereas the spectrum of the pattern in hyperbolic regime (g) tends to align one of the asymptotes of the hyperbola depicting modulation instability gain. The Fourier spectra of the states (b) and (f) are presented in (d) and (h).

Full size image

Spatiotemporal two-dimensional dissipative soliton. We also generate a localized 2D dissipative solitons51 traveling along the circumference of the chain, which we describe in the following. To generate this spatiotemporal Kerr soliton (2D-DKS), we pump the 4th supermode in the elliptic regime (blue asterisk at k = 4 in Fig. 1b with ∣fℓ∣ = 2.35 and ζ0 = 10.92, so the local dispersion has anomalous sGVD \({j}_{2}=j{(\pi /10)}^{2}\cos 2\pi /5=0.30\) in addition to the non-zero supermode FSR \({j}_{1}/2\pi =0.1j\sin 2\pi /5=0.95\). The obtained solution of the 2D-DKS corresponds to a continuously re-circulating spatial discrete soliton (cf. Supplementary Movie 4) that forms an ellipse with a fish-like tail in the spectral domain (cf. Fig. 5a, b). Similar to Cherenkov radiation for conventional DKS, the disk-shaped soliton crosses the hybridized dispersion in the vicinity of the edge of the Brillouin zone (cf. Fig. 5c), resulting in the intensive generation of the dispersive waves, forming the fish-like spectrum, but presuming the soliton coherence. In the leading order, such 2D soliton is described by 2D LLE, therefore its approximate existence range can be inferred from51.

Fig. 5: Localized 2D dissipative soliton in a chain of 20 resonators.
figure 5

Instantaneous field profile in the chain of resonators and the corresponding 2D spectral profile in dB are shown in panels (a) and (b). Inset in (a) shows the roundtrip number of the soliton in time. c Schematics of the soliton as a dispersionless structure (blue disk) beneath the hybridized dispersion surface (similar to Fig. 1a, spans over 1.25 of the Brillouin zone along k axis). Intersection between the soliton disk and the dispersion defines the position of the dispersive waves taking the form of a `fish tail' in panel (b). d Field dynamics on a single resonator level with an inset resolving one pulse. Color represents the amplitude in dB (see colorscale in panel a), the cross-sections of the inset are in linear scale normalized on the average amplitude in the cavity. e The corresponding super-resolution and averaged spectrum.

Full size image

On the single resonator level, the optical field envelope demonstrates breathing dynamics (Fig. 5d) due to the periodic appearance of the pulse in every individual resonator constituting the chain. Resolving the field envelope dynamics in time, one detects the periodic appearance of optical pulses and adjacent dispersive waves. Sampling this signal in time and computing the overall Fourier transform gives the so-called super-resolution spectrum shown in Fig. 5e. The periodic nature of the signal reveals a typical comb spectrum, with the presence of a fine spectral structure around each comb line, shown in the inset of Fig. 5e. These subcombs appear due to the breathing dynamics and emergence of the corresponding dispersive waves, and the number of spatial modes does not define the number of these subcombs. In fact, these subcombs correspond to just low-frequency breathing, which is also present in the single resonator case in the breathing regime15. The time-averaging of the signal yields a smooth spectral profile (solid line in Fig. 5e), indicating the periodic nature of the signal. Noteworthy, a similar (in terms of hybridized dispersion) 2D-DKS was observed in the edge state of the Haldane model37. However, the soliton coherence of the observed structure suffered from the presence of the bulk, which effect we investigate below with an example of the edge states of the SSH model.

Edge state solitons of Su-Schreiffer-Heeger model as solitons in a single resonator

We continue our analysis considering the case of a chain with staggered couplings, namely the SSH model (Fig. 1c), in which the band structure has bands with different dimensionality. While the dynamics of the bulk should be close to the case described above, the edge states are localized on the corners of the chain. The corresponding eigenvalues λedge represent a 0D band. Thus, the hybridized dispersion profile corresponds to a conventional integrated dispersion of a single microresonator as shown in Fig. 1d. The chain supports edge states in the case where inter-cell coupling Jinter is bigger than intra-cell coupling Jintra (i.e., the topological phase shown in Fig. 1c). In the limit Jintra → 0 (a trivial edge state32), the first resonator is completely decoupled from the chain, and its dynamics is described by conventional LLE. With the finite ratio Jintra/Jinter < 1, the formed band structure (see Fig. 1c) has upper and lower bulk regions with eigenmodes in the middle of the gap that correspond to the edge states52. With the chromatic dispersion taken into account, the nonlinear interactions happen on the hybridized dispersion surface. Due to the nontrivial topology, the hybridized dispersion of the bulk has a form of a two-dimensional surface, while the edge states have a 1D dispersion curve. To generate an edge soliton, one needs to pump the edge state (c0 is the corresponding amplitude). Neglecting the presence of the bulk states (cj ≪ c0), according to Eq. (3), the governing equation takes the form of a simple LLE. This analogy helps further to understand the soliton interaction with the bulk states. Generation of the edge soliton corresponds to the formation of the dispersionless line below the edge state parabola (schematically shown in Fig. 1c). If the width of the bandgap is large enough (effectively corresponds to the limit Jintra/Jinter → 0, Jinter ≫ κ), the dynamics of the soliton will be similar to the single-resonator dynamics, because the field will be still localized in the first ring. However, if the soliton line crosses the lower bulk band, additional photon transfer to the bulk modes will occur (a similar effect has already been observed in the system of just two coupled resonators considered in24). The photons scattered to the bulk will experience now 2D dynamics and can drastically affect the soliton stability and existence range.

To demonstrate this effect, we simulated an SSH chain of 10 resonators with typical parameters of Si3N4 photonic microcombs: κ0/2π = 50 MHz, D2/2π = 4.1 MHz, Jinter/2π = 5 GHz, D1/2π = 182 GHz, Jintra/2π = 1 GHz under 100 mW pump power (that corresponds to the normalized pump f 2 = 223 for the normalization) with critically coupled (κex = κ0) first resonator. We excited the edge state resonance in the conventional way, scanning the pump laser from the blue- to red-detuned zone. We show the intracavity power in the first (blue line) and second (red line) resonators as a function of detuning in Fig. 6a along with the limit case of a decoupled single resonator (black line). As one can clearly see, the power dynamics in the first resonator generally has the same features as the decoupled resonator, but the soliton existence range (δω ≈ 27.2κ/2) is shortened in the case of the SSH chain (δω ≈ 21.0κ/2). In fact, the power in the second resonator reveals several resonance features with increased detuning. Investigating the field and spectral profiles of the DKS (detuning δω = 2π ⋅ 1.48 GHz = 14.8κ/2) itself in these resonators (cf. Fig. 6b, c), one can see that the soliton has a smooth sech profile in the first cavity, while there is a strong background modulation in the second with the soliton amplitude 200 times smaller. The reconstructed NDRs (Fig. 6d, e) reveal that the soliton, formed below the edge parabola crosses the lower bulk modes that lead to the generation of the dispersive waves in the second resonator, mixing the edge and bulk states. While here we presented a case of moderate edge-bulk interaction employing a single set of parameters used in recent experiments 24,25,53, stronger interactions can occur for spectrally broader solitons (smaller ratio D2/κ) or narrow bandgaps. Nevertheless, our conclusions remain valid for a smaller gap size and can be generalized for higher dimension topological lattices: due to the presence of the other bands, the generated edge-state soliton (be it DKS or 2D-DKS) induces edge-to-bulk scattering that influences soliton stability and can result in its temporal decoherence. However, it should be noted that according to the nonlinear term in Eq. (3), rigorous estimation of the efficiency of the nonlinear interactions between the edge and bulk states depends on the spatial overlap between the eigenstates \({{\mathbb{V}}}_{j}\). Thus, in order to quantitatively characterize the scattering mechanism, one needs to compute the eigenstates and the corresponding overlap, but this research is beyond the scope of the current manuscript.

Fig. 6: Soliton dynamics at the edge state of the Su-Schrieffer-Heeger model (SSH).
figure 6

a Intracavity power as a function of detuning in the first (solid blue line), second resonators (solid red line), and for the first resonator completely decoupled from the chain (solid black line). Vertical dashed line shows the detuning at which the soliton state is resolved below. b, c Temporal and spectral profiles of the soliton in the first (blue lines) and second (red lines) resonators normalized on the peak power in the first resonator. d, e The corresponding nonlinear dispersion relations. White dots represent the hybridized dispersion in the linear regime.

Full size image

Conclusions

We theoretically described nonlinear interactions via four-wave mixing (i.e. parametric oscillations) in lattices of driven photonic microresonators. We showed the hybridization of the chromatic dispersion with the N-spatial dimensional band structure gives rise to an effective (N+1)-dimensional dispersion surface that governs the FWM processes with the conservation law defined by the structure of the lattice’s eigenfunctions. Further, we analytically and numerically explored the nonlinear dynamics of the 1D band in a chain of equally coupled resonators. We demonstrated that this system possesses a 2D dispersion surface and can be described in the long wavelength limit by the 2D LLE at its local extrema. Different parts of the dispersion surface correspond to two fundamentally different regimes of operation: elliptic and hyperbolic. This results in different local dispersion topography. Simulating the full set of coupled LLEs, we demonstrated nonlinear effects inherent to 2D systems which include Turing pattern formation, 2D spatial-temporal dissipative Kerr solitons, and wave collapses in the chaotic state. Considering the SSH model, we demonstrated that 0D bands that correspond to the edge state can be approximated by the conventional 1D-LLE. However, within the range of experimentally accessible parameters for state of the art nonlinear integrated platforms that support generation sufficiently broad DKS, the overlap of the generated edge-state DKS with the bulk states can lead to the DKS-induced edge-bulk mixing and consequently perturb the soliton stability. In summary, our theory sheds light on nonlinear interactions in integrated photonic lattices and will be helpful to guide future experimental investigations of multi-mode systems with complex band structures, and highlight the limitation of topological protection when it comes to the formation of Kerr frequency combs in lattices.

Methods

Numerical simulations

The nonlinear dynamics in the chain of 20 coupled resonators is modeled using step-adaptative Dormand-Prince Runge-Kutta method that is implemented in Python-based library PyCORE https://github.com/ElKosto/PyCORe/tree/PyCORe++ with included integrator from Numerical Recipes 3. The normalized parameters of the simulated system in Eq. (5) are: d2 = 0.04, j = 10.00. The corresponding realistic Si3N4 parameters are: κ0/2π = κex/2π = 50 MHz, J/2π = 0.5 GHz, D2/2π = 4.1 MHz, FSR = 182 GHz.

Wave collapse

To observe the wave collapse in the elliptic regime, we fix the detuning at ζ0 = 22.1. Each resonator is pumped with a power of fℓ = 2.35 with equal relative phases. To reconstruct the incoherent dynamics in the hyperbolic regime, we fix the detuning at ζ0 = −17.0 and use the same pump power. However, we alternate the phases of the pump by π to excite only the supermode k = N/2. In both cases, we employ 1024 sampling points to resolve the angular dynamics within each resonator and 20,000 sampling points to resolve the temporal dynamics.

Turing patterns

To excite the Turing patterns, we first induce incoherent dynamics in the cavity and then tune the pump laser from the blue to the red-detuned side of the resonance (i.e., decreasing ζ0). For the elliptic regime, we observe stable pulses at fℓ = 1.05 and ζ0 = 20.5, and for the hyperbolic regime at fℓ = 2.35 and ζ0 = −20.3. We employ the Newton-Raphson method for finding stationary solutions to verify the stability of such structures. Using the simulation data as an initial seed solution, we then apply the gradient descent method to converge to the stationary solutions shown in Fig. 4.

2D spatio-temporal dissipative soliton

To observe the generation of the 2D soliton, we fix the pump power at ∣fℓ∣ = 2.35 and set the relative phase to 2π/5 to excite the 4th spatial supermode in Fig. 1a. We set the laser detuning ζ0 such that the system is in a chaotic state, then we gradually reduce the detuning value to ζ0 = 10.92, where we observe the formation of the soliton.

Edge state soliton in the Su-Schrieffer-Heeger model

We use modified Eq. (5) to simulate the dynamics of the 10 resonator Su-Schrieffer-Heeger (SSH) chain. To take into account the chain with open boundary conditions, we consider 1st and 10th resonators coupled only to one of its neighbors, but decoupled from each other. The resonator parameters, such as κ0, κex, D2, and FSR, are taken to be the same as for the closed chain. The inter-cell coupling equals to Jinter/2π = 5 GHz, the intra-cell Jintra/2π = 1 GHz. The chain consists of 10 resonators, and the bus waveguide is only coupled to the first and last resonators. To excite the edge state, we fix the pump power at 100 mW which is equivalent to f2 = 22 in the normalized units. The edge state resonance is located at ζ0 ≈ 0, and we sweep the laser frequency from the blue to the red-detuned side (increasing ζ0). The single-resonator transmission trace presented in Fig. 6a is obtained using the standard Lugiato-Lefever equation (i.e., Eq. (5)) with zero coupling terms. The resonator and pump laser parameters are chosen to be the same as for the excitation of the edge state in the SSH model.