Introduction

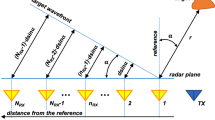
Small displacement measurement using a micro-Doppler radar such a non-contact vital signal sensing has been extensively studied. Respiration, heartbeat rate, and heart rate variability are the parameters of most interest to researchers. Respiration sensing and apnea analysis1,2,3 have been widely researched, and related off-the-shelf products have been released. In particular, heartbeat signals have been intensively investigated4,5,6,7,8,9,10 where continuous wave (CW) radars have been used to detect displacement smaller than 1 mm on the human chest. The CW radar is a simple single transmitter and receiver with a single oscillator, in which the receiver coherently mixes the received signal down to the baseband by the oscillator. The CW radar has the so-called null point detection problem in which the baseband signal becomes null. This happens when the distance between the radar and a target is a multiple of π. Some literature using single mixer receiver researched to solve this problem11,12,13,14. Common point of the literature is that the null problem can be solved by using a phase tuning of the received and reference signal. The lack of these methods is how the receiver always reach the optimum, which is still under studying. Another one is that tunable RF phase shifting device is currently expensive and difficult to control in practice at high frequency band. Another method to solve the null problem is by using quadrature mixer receiver architecture9, in which the receiver has two orthogonal mix-down branches as shown in Fig. 1, where the two baseband signals are called in-phase (I) and quadrature-phase (Q) signals. This type of radar is called the quadrature continuous-wave (QCW) radar. To get useful information from direct-current (DC) of the baseband, the receiver is assumed to have the DC-coupled structure in this paper.

Figure 1
figure 1

The QCW radar architecture.

Full size image

Small displacement induces the phase change of the baseband signal of the QCW radar, and it can be detected by linear or non-linear demodulation method4. Linear demodulation method finds it by assuming that it is linear to the baseband signal itself; this is valid when the displacement is much smaller than the oscillator wavelength such as displacement <λ/4π4. Differently from linear demodulation, non-linear demodulation gets the small displacement by calculating arctangent function of the baseband signal as arctan(Q/I) which gives accurate measurement of the displacement. Unfortunately the accuracy cannot be maintained unless the impairment from the QCW radar is compensated, more specifically from the radar itself and its environment. As many research articles addressed, the impaired baseband signal of the QCW radar has I/Q imbalance and DC-offset4,15,16,17. I/Q imbalance is the mismatch of magnitude or delay between the I and Q signal paths. As described in Yan et al.9 I/Q imbalance introduces errors in the arctangent function, thus it deteriorates the radar accuracy. To measure it, a phase shifter18 or a mechanical moving stage19 makes sufficient Doppler shifted signals and the baseband I and Q signals are compared. The measured imbalance can be eliminated simply by using Gram-Schmidt procedure 21. The DC-offset is the bias offset of the baseband signal, where the offsets of I and Q signals are usually different. The DC-offset also affects significant performance degradation of the QCW radar4,17,20,21. It is caused by hardware system imperfections and/or environment effect in-between the radar and a target4. If the sufficient Doppler shift is made, the baseband signal makes elliptic arc in the complex plane of the signal. By estimating the center of the ellipse, the DC-offset can be determined16. Several center estimation algorithms have been studied to measure the DC-offset5,16,17,22,23. One heuristic method using I/Q-rotation was presented in Park et al.16, however it is computationally complex but the performance is poor. The enhanced fitting algorithm was used for the center estimation in Zakrzewski et al.5, where the Levenberg-Marquardt (LM) algorithm, a positive definite geometric fitting method, is used and its performance was compared with the Park’s algorithm. Algebraic fitting method for \({\ell }_{1}\)-minimization was proposed for the center estimation17,22,23, where its performance is better than the existing \({\ell }_{2}\)-based minimization algorithms against noisy data. However, the disadvantage of the \({\ell }_{1}\)-minimization is that the computationally-high linear programming is required and its real-time implementation is still be open problem.

Common point in the literature is that the center estimation performance increases when the elliptic arc is sufficiently long. To secure such a long arc, a pre-calibration step is preferred for radar systems. Usually, the pre-calibration step is performed using the calibration environment, where a metallic sphere object is placed on a mechanical moving stage. And a radar system is arranged in a straight line with the object i.e. the target. Then by controlling the stage, sufficiently long arc is generated. However, this pre-calibration fails when the center of the arc frequently changes. Actually, it changes as time goes or as the environment around the radar system changes. When the radar measures small displacement smaller than 1 mm on the human chest, it is difficult to secure such long arc. Gao et al.20 presented a center estimation error reduction method by correcting the estimated radius of the short arc. However, this work still requires the cumbersome calibration environment, in which the estimation data set of long arc is necessary to the radius correction of the short arc. Huang et al.17 presented a semi-definite programming algorithm for center estimation of the short arc. It requires no calibration environment, and the center estimation is performed using only the target’s small displacement. The estimation performance is comparable to the other algorithms using the calibration environment. Disadvantage of the semi-definite programming is high computational complexity, where the worst case complexity is bounded to O(n6). Another approach to make sufficiently long elliptic arc without pre-calibration step is proposed24,25. In the literature, RF phase is controlled by shifting antenna mechanically24 or by using RF transmitter phase shifter25, where additional devices are required to the radar such as machine stages24 and RF phase shifters25. At high frequency bands over 10 GHz, the high-precision machine stages and high-frequency phase shifters are currently expensive making them difficult to apply in the radar.

The previous works are all based on the center estimation of a single arc because the QCW radar uses a single-tone frequency. In this paper, we discuss the center estimation based on multiple arcs and propose the quadrature frequency-group (QFG) radar in which multiple discrete arcs are generated by a group of frequencies. The discrete arcs of the QFG radar constitute a sufficiently long elliptic arc even with the small displacement. Thus, the QFG radar requires no calibration environment, and it can be used directly in the measurement. The QFG radar requires no additional devices such as stages or RF phase shifters. Properties of the discrete arcs such as the arc length and interval are presented in terms of the frequency group. The performance improvement of the QFG radar is presented through several computer simulations such as for different carrier frequency bands, different SNRs, and different fitting algorithms. With the QFG radar, the existing \({\ell }_{2}\)-based minimization algorithms show quite well performance, where the performance of geometric and algebraic fitting algorithms are presented. Experiments are performed in a quantitative test setup for the 24 GHz short-range radar system. In the test setup, the radar is closely located to a target, which is a common occurrence during human vital signal measurement. Low transmit power is assumed because of electromagnetic wave influence against human body, and the target has only small displacement such as 0.5 mm. The experimental results show that the fitting accuracy of the QFG radar is up to 100 times better than the QCW radar.

Methods

Micro-Doppler Monitoring of Small Displacement

Principle of the QCW radar

The QCW radar shown in Fig. 1 transmits a stable wave energy with frequency f, which is expressed as

$$s(t)={A}_{tx}\,\cos \,(2\pi ft+\varphi (t)),$$
(1)

where ϕ is the random phase noise of the transmitter. The transmitted signal is reflected from a target within the radar radiation area. The received baseband signal shown in Fig. 1 is written as

$$\begin{array}{rcl}r(t) & = & {A}_{0}\,\cos \,(4\pi {\lambda }^{-1}d+4\pi {\lambda }^{-1}x(t)+{\phi }_{0}+{\rm{\Delta }}\varphi (t))\\ & & +\,j{A}_{0}{A}_{e}\,\sin \,(4\pi {\lambda }^{-1}d+4\pi {\lambda }^{-1}x(t)+{\phi }_{0}+{\rm{\Delta }}\varphi (t)+{\varphi }_{e})\\ & & +\,D{C}_{I}(t)+jD{C}_{Q}(t)+w(t),\end{array}$$
(2)

where is A0 the baseband amplitude, λ is the wavelength of the transmitter frequency f, d is the nominal distance between the radar and a target (human chest in this paper), x(t) is the small displacement of the target (|x(t)| < λ), φ0 is the initial phase offset, Δϕ is the phase noise difference between the phase noise and the time-delayed phase noise, and w(t) is white Gaussian noise. The Gaussian noise variance σ is written as \(\sqrt{{A}_{0}^{2}/(2\cdot SNR)}\). Ae and ϕe are amplitude and phase imbalance of the in- and quadrature-phase paths, which is mainly caused by circuit imperfection factors of the radar. Generally, the IQ-imbalance is measured at controllable test environment and corrected by the Gram–Schmidt procedure15

$$\begin{array}{rcl}[\begin{array}{c}{r}_{c,I}(t)\\ {r}_{c,Q}(t)\end{array}] & = & [\begin{array}{cc}1 & 0\\ -\tan \,{\varphi }_{e} & \frac{1}{{A}_{e}\,\cos \,{\varphi }_{e}}\end{array}]\,[\begin{array}{c}{r}_{I}(t)\\ {r}_{Q}(t)\end{array}]\\ & = & {A}_{0}\,\cos \,(4\pi {\lambda }^{-1}d+4\pi {\lambda }^{-1}x(t)+{\phi }_{0}+{\rm{\Delta }}\varphi (t))\\ & & +\,j{A}_{0}\,\sin \,(4\pi {\lambda }^{-1}d+4\pi {\lambda }^{-1}x(t)+{\phi }_{0}+{\rm{\Delta }}\varphi (t))\\ & & +\,D{C}_{I}(t)+jD{C}_{Q}(t)+w(t).\end{array}$$
(3)

DCI and DCQ in (2) are the DC-offsets of the in- and quadrature-phase paths. The DC-offset is known to be caused by reflections from target’s position as well as hardware imperfections4. The DC-offset induced by hardware imperfection can be easily eliminated by the pre-measurement method. If the target is stationary, the remaining DC-offset is constant. Otherwise, it is likely to change over time as the target position varies. If the DC-offset changes slowly, it can be said that it is constant for some short time interval. With this assumption, also called quasi-stationary, (3) can be written as

$$\begin{array}{rcl}{r}_{i}(t) & = & {A}_{0,i}\,\cos \,(4\pi {\lambda }^{-1}{d}_{i}+4\pi {\lambda }^{-1}x(t)+{\phi }_{0}+{\rm{\Delta }}\varphi (t))\\ & & +\,j{A}_{0,i}\,\sin \,(4\pi {\lambda }^{-1}{d}_{i}+4\pi {\lambda }^{-1}x(t)+{\phi }_{0}+{\rm{\Delta }}\varphi (t))\\ & & +\,D{C}_{I,i}+jD{C}_{Q,i}+w(t),\end{array}$$
(4)

where 0 ≤ t < T, i = 0, 1, 2, …, ri(t) = r(t − iT), and T is the quasi-stationary time interval. This assumption is reasonable in the case of the vital signal measurement where the chest displacement frequency is much slower than the radar sampling rate.

We assume that the phase noise is small Δϕ(t) ≈ 0, then (4) can be simply written as

$$\begin{array}{rcl}{r}_{i}(t) & \simeq & {A}_{0,i}\,\cos \,(4\pi {\lambda }^{-1}{d}_{i}+4\pi {\lambda }^{-1}x(t)+{\phi }_{0})\\ & & +\,j{A}_{0,i}\,\sin \,(4\pi {\lambda }^{-1}{d}_{i}+4\pi {\lambda }^{-1}x(t)+{\phi }_{0})\\ & & +\,D{C}_{I,i}+jD{C}_{Q,i}+w(t).\end{array}$$
(5)

When SNR is high, (5) can be plotted as a part of a circle in a complex plane as shown in Fig. 2. d gives no information in the complex plane because d is shown as multiple rotations tracing on the dotted circle. To simplify the explanation, we eliminate the d term in this section as

$${r}_{i}(t)\simeq {A}_{0,i}\,\cos \,(4\pi {\lambda }^{-1}{x}_{i}+{\phi }_{0})+j{A}_{0,i}\,\sin \,(4\pi {\lambda }^{-1}{x}_{i}+{\phi }_{0})+D{C}_{I,i}+jD{C}_{Q,i}+w(t).$$
(6)
Figure 2
figure 2

Complex plot representation of ri(t): ri(t) due to the displacement x(t) is located in the thick arc.

Full size image

After the estimation of the center of the circle (DCI, DCQ) the displacement xi can be obtained by linear and non-linear demodulation methods4,26,27. With the arctangent demodulation4, the displacement x(t) is easily obtained as

$$\arctan (\frac{\sin \,(4\pi {\lambda }^{-1}x(t)+{\phi }_{0})}{\cos \,(4\pi {\lambda }^{-1}x(t)+{\phi }_{0})})=4\pi {\lambda }^{-1}x(t)+{\phi }_{0}.$$
(7)

Various methods have been studied to estimate the center of circle5,16,17,28. In Park et al.16, ri(t) was first rotated parallel to the Q-axis. After the rotation DC-offset exists only on the I-axis, i.e., \((\hat{k},0)\). Then, \(\hat{k}\) for two different time t1 and t2 is obtained by the following heuristic estimator

$$\hat{k}=median[\frac{{|{r}_{i}({t}_{1})|}^{2}-{|{r}_{i}({t}_{2})|}^{2}}{2Re\{{r}_{i}({t}_{1})-{r}_{i}({t}_{2})\}}].$$
(8)

The matrix of eigenvectors of the covariance matrix of ri(t) transforms the arc of ri(t) parallel to Q-axis, where the arc refers to the deviation of ri(t). This method is called Park method.

Unlike Park et al.16, Zakrzewsk et al.5 used a traditional circle fitting method, namely “geometric fit”, to estimate the center of circle. The DC-offset is obtained by minimizing the following function based on the geometric distance

$$E=\sum _{n=1}^{N}\,{(\sqrt{{(real({r}_{i}({t}_{n}))-D{C}_{I,i})}^{2}+{(imag({r}_{i}({t}_{n}))-D{C}_{Q,i})}^{2}}-R)}^{2},$$
(9)

where R is the radius of the fitting circle. Zakrzewsk et al.5 showed that (9) can be minimized by the classical Gauss-Newton method with the Levenberg–Marquardt (LM) correction factor λ. This method is called LM method. Details of this method are presented in Chernov et al.28. The Park method and LM method were compared in Zakrzewsk et al.5 through simulations and human respiration test. Computation time of the Park method is longer than the LM method because the eigenvalue calculation of covariance matrix in the Park method has higher computational complexity than the iterative operations in the LM method. In Zakrzewsk et al.5, it was shown that the LM method performs better than the Park method when the displacement is simple sinusoidal or complicated respiration.

Quadrature Frequency-Group Radar

For the QFG radar, the oscillator frequency f should be variable. To achieve this, two widely used architectures, step-frequency CW (SFCW) modulation and orthogonal-frequency-division-multiplexing (OFDM) modulation as depicted in Fig. 3(a,b), can be used29,30,31,32,33,34. The baseband signal in Fig. 3(a) is written as

$$\begin{array}{rcl}{r}_{i}(t,{f}_{m}) & = & {A}_{0,i}(m)\,\cos \,(4\pi {c}^{-1}{f}_{m}p(t)+{\phi }_{0})\\ & & +\,j\cdot {A}_{0,i}(m)\,\sin \,(4\pi {c}^{-1}{f}_{m}p(t)+{\phi }_{0})\\ & & +\,D{C}_{I,i}+jD{C}_{Q,i}+w(t),\end{array}$$
(10)

where fm is the discrete frequency value that is controlled by the oscillator, m = 0, …, M − 1, and p(t) = di + x(t). If the frequency sweep time is sufficiently fast, the displacement x(t) is considered to be constant for the sweep time. Therefore, (10) can be written as

$$\begin{array}{rcl}{r}_{i}(n,{f}_{m}) & = & {A}_{0,i}(m)\,\cos \,(4\pi {c}^{-1}{f}_{m}p(n)+{\phi }_{0})\\ & & +\,j\cdot {A}_{0,i}(m)\,\sin \,(4\pi {c}^{-1}{f}_{m}p(n)+{\phi }_{0})\\ & & +\,D{C}_{I,i}+jD{C}_{Q,i}+w(n),\end{array}$$
(11)

where pi(n) = di + x(n), and w(n) is considered as a 2D Gaussian distribution with zero mean. The noise variance is expressed as signal-to-noise ratio (SNR). (11) is the baseband signal of the QFG radar. The QFG radar can also be implemented as in Fig. 3(b), where the frequency of the oscillator is fixed. But the transmitted baseband signal, sI(t) and sQ(t), is an OFDM symbol that is multiplexed by multiple frequency signals where each signal is orthogonal to the others. By multiplying the received baseband signal by the transmitted symbol which is a well-known method in OFDM communication systems, the same signal as (11) can be obtained. Thus, the QFG radar can be implemented through the above SFCW and OFDM architectures. We use the SFCW architecture in this paper.

Figure 3
figure 3

The QFG radar architecture: (a) SFCW-type and (b) OFDM-type.

Full size image

The set of frequencies, i.e., F = {f0, f1, …, fM−1} = {fc, fc + Δf, …, fc + (M − 1) · Δf} lies within a frequency band, where fc is the carrier frequency of F, and Δf is the adjacent frequency difference. The popular carrier frequency bands of radar systems are 2.4 GHz, 10 GHz, 24 GHz, and etc. For these bands, a set of frequencies can be collected whose received signal power values do not vary considerably over F. For example, Fig. 4(a) shows the received signal power of fc = 24 GHz and Δf = 30 MHz, and Fig. 4(b) shows the received signal power of fc = 2.4 GHz and Δf = 3 MHz, where the transmitted signal power is assumed to be 1 mW and the path loss of the transmitted signal is considered as the free-space path loss equation35 as follows

$$FSPL(p(n),{f}_{m})=20lo{g}_{10}(p(n){f}_{m})-147.55,$$
(12)

where p(n) is set to 1 m. In the figures, the variance of the received signal powers is less than 1 dB. This kind of frequency set F is called a frequency group in this paper. In this case, it can be assumed that A0,i(m) is independent of m. Thus (11) can be written as

$${q}_{i}(n,{f}_{m})={A}_{0,i}exp[j4\pi {c}^{-1}{f}_{m}p(n)+{\phi }_{0}]+(D{C}_{I,i}+jD{C}_{Q,i})+w(n)$$
(13)
Figure 4
figure 4

Received signal power (Transmission signal power is assumed to 1 mW): (a) 24 GHz band and (b) 2.4 GHz band.

Full size image

(13) is hold in the rest of this section, and the effect of the assumption (13) on the center estimation performance will be discussed later. Then, (13) is an arc function of fm and p(n) on a circle with its center and radius is (DCI,I, DCQ,i, A0,i). In this section, we assume that the dc-offset (DCI,I, DCQ,i) is zero for ease of explanation. For di = 30 cm and 0 < x(n) < 1 mm, the baseband signal of the QFG radar produces four arcs in complex plane as shown in Fig. 5(a), in which frequency group is set as {fc = 24 GHz, Δf = 30 MHz, M = 3}. If Δf is reduced to 20 MHz, the arcs are overlapped as in Fig. 5(b). This shows that the arc can be extended by the QFG radar that makes up Δf and M.

Figure 5
figure 5

Multiple arcs of the QFG radar for Δx = 1 mm: (a) Δf = 30 MHz and (b) Δf = 20 MHz.

Full size image

The interval of two adjacent arcs as shown in Fig. 6(a) can be obtained by

$${I}_{d}=\angle {q}_{i}(n,{f}_{m+1})-\angle {q}_{i}(n,{f}_{m})=4\pi {c}^{-1}{\rm{\Delta }}f\cdot d,$$
(14)

where \(\angle {q}_{i}(n,{f}_{m})\) is the angle of qi(n, fm), and Id depends on d and Δf. Let Δx the absolute displacement of x(n), and the arc length due to the displacement Δx at fm as shown in Fig. 6(a) is written as

$${l}_{{\rm{\Delta }}x}(m)={A}_{0,i}4\pi {c}^{-1}({f}_{c}+m{\rm{\Delta }}f){\rm{\Delta }}x,$$
(15)
Figure 6
figure 6

Arc length \({\rm{\Delta }}{\vartheta }_{x}(m)\) is almost constant with respect to m: (a) 24 GHz band and (b) 2.4 GHz band.

Full size image

As a rule of a thumb, Δx is less than the order of 10−3, fc is greater than the order of 109, and Δf is greater than the order of 106. Then, lΔx(m) is almost constant over m = 0, …, M − 1. Figure 6 shows lΔx(m) of the arcs shown in Fig. 5, where the average length of the arcs is 103 times greater than the maximum difference length of the arcs. The design of the QFG radar is simplified by approximating lΔx(m) to lΔx, thus (15) is written as

$${l}_{{\rm{\Delta }}x}={A}_{0,i}4\pi {c}^{-1}{f}_{c}{\rm{\Delta }}x,$$
(16)

Using (14) and (16), we can determine the parameter of the QFG radar such as fc, Δf, and M according to a given Δx and d. For example, consider that Δx = 0.1 ~1 mm and d = 30 cm (mostly, respiration and heartbeat radars have this range of Δx. First, we should determine fc of which wavelength is greater than Δx. For Δx = 1 mm, we selected fc = 24 GHz of which wavelength is sufficiently greater than the maximum Δx = 1 mm. Assuming that A0,i = 1, lΔx ≈ 1 and then we can determine Δf using (14) by considering how much we separate the adjacent arcs. By selecting Δf = 30 MHz, Id ≈ 0.377 and the adjacent arcs are located as shown in Fig. 7(a), where arcs are properly placed and slightly overlapped. Because lΔx ≈ 1 is small, we need to extend it using M. For M = 4, the arc length is extended to almodt four times as shouwn in Fig. 7(a). If Δf = 40 MHz, total length of the arcs are longer than Δf = 30 MHz but the arcs are discontinuously placed as depicted in Fig. 7(b). For small displacement such as Δx = 0.1 mm, Δf should be set small and bigger M if you want to get continuously placed long arcs. By reducing Δf to 5 MHz, the arcs are continuously placed in contrast to Δf = 30 MHz, which are shown in Fig. 7(c,d), respectively. These arcs are directly related to the performance of their center estimation algorithms as will be presented in the following sections.

Figure 7
figure 7

Examples at fc = 24 GHz, M = 4: (a) Δf = 30 MHz for Δx = 1 mm, (b) Δf = 40 MHz for Δx = 1 mm (c) Δf = 30 MHz for Δx = 0.1 mm, and (d) Δf = 5 MHz for Δx = 0.1 mm.

Full size image

Center Estimation of the QFG Radar

We starts from (11) with M = 3. Three algorithms are presented to estimate the center of (11) for the QFG radar: the circumcenter method (computationally simple)36, the Pratt method (algebraic fitting)37, and the LM method (geometric fitting)38. The circumcenter calculation method is as follows. Three points are selected as \(S=[{y}_{i}(n,{f}_{0})\,{y}_{i}(n,{f}_{1})\,{y}_{i}(n,{f}_{2})]\). Then, the area of S, ΔS, is calculated. If \({\rm{\Delta }}S > \epsilon \), the circumcenter can be calculated as

$$({\widehat{DC}}_{I},{\widehat{DC}}_{Q})=\frac{\alpha {S}_{1}+\beta {S}_{2}+\gamma {S}_{3}}{\alpha +\beta +\gamma },$$
(17)

where \(\epsilon \) is a small value, e.g., 10−9, α = a(b + c − a), β = b(a + c − b), γ = c(a + b − c), a = |S2 − S3|, b = |S1 − S3|, and c = |S1 − S2|. If \({\rm{\Delta }}S < \epsilon \), another S should be taken for other n until \({\rm{\Delta }}S > \epsilon \). If there is no S that satisfies \({\rm{\Delta }}S > \epsilon \), the method fails. If Δf is carefully designed considering fc, d, and Δx, the method would not fail. This method is summarized in Fig. 8.

Figure 8
figure 8

Circumcenter method: (a) If area \({\rm{\Delta }}S > \epsilon \), the \(({\widehat{DC}}_{I},{\widehat{DC}}_{Q})\) is the circumcenter of the triangle S. (b) Flowchart.

Full size image

The Pratt method is algebraic circle fitting, which is a non-iterative procedure. Thus, the method is computationally efficient compared to the iterative geometric fitting method such as LM method. The algebraic fitting is the minimization of a circle polynomial:

$${ {\mathcal F} }_{ab}(A,B,C,D)=\sum _{j=0}^{J-1}\,\sum _{m=0}^{M-1}\,{z}^{2}(j,m),$$
(18)

where \(z(j,m)=A{|{y}_{i}(j,{f}_{m})|}^{2}+B\cdot Re\{{y}_{i}(j,{f}_{m})\}+C\cdot Im\{{y}_{i}(j,{f}_{m})\}+D\) is called the circle polynomial or the algebraic distance. The Pratt method37 is the gradient weighted algebraic fitting that minimizes

$${ {\mathcal F} }_{Pratt}(A,B,C,D)=\sum _{j=0}^{J-1}\,\sum _{m=0}^{M-1}\,\frac{{z}^{2}(j,m)}{{\Vert \nabla z(j,m)\Vert }^{2}},$$
(19)

where ∇ is the function gradient operator. By approximating z(j, m) ≈ 0, (19) can be simplified as

$${ {\mathcal F} }_{Pratt}(A,B,C,D)=\sum _{j=0}^{J-1}\,\sum _{m=0}^{M-1}\,\frac{{z}^{2}(j,m)}{{B}^{2}+{C}^{2}-4AC},$$
(20)

Minimization of (20) is equivalent to the minimization of (19) with the constraint B2 + C2 − 4AC = 137. With the Lagrange multiplier η, the minimization can be written as

$${{\rm{G}}}^{T}({{\rm{X}}}^{T}X){\rm{G}}-\eta ({{\rm{G}}}^{T}H{\rm{G}}-1),$$
(21)

where G = [A B C D]T,

$${\rm{H}}=[\begin{array}{cccc}0 & 0 & 0 & -2\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ -2 & 0 & 0 & 0\end{array}],$$
$${\rm{X}}=[\begin{array}{c}{\rm{Y}}(0)\\ \vdots \\ {\rm{Y}}(J-1)\end{array}],$$

and

$${\rm{Y}}({\rm{n}})=[\begin{array}{cccc}{|{y}_{i}(n,{f}_{0})|}^{2} & Re\{{y}_{i}(n,{f}_{0})\} & Im\{{y}_{i}(n,{f}_{0})\} & 1\\ \vdots & \vdots & \vdots & \vdots \\ {|{y}_{i}(n,{f}_{M-1})|}^{2} & Re\{{y}_{i}(n,{f}_{M-1})\} & Im\{{y}_{i}(n,{f}_{M-1})\} & 1\end{array}].$$

(21) is differentiated with A as follows:

$${{\rm{H}}}^{-1}({{\rm{X}}}^{T}X){\rm{G}}-\eta {\rm{G}}=0,$$
(22)

Hence (22) is the (η, G)-problem of the matrix H−1(XT X), where η is the smallest non-negative eigenvalue and A is its eigenvector. In this paper, we solve the problem using the numerically stable singular value decomposition (SVD) of X, X = U∑VT. After SVD, compute W = V∑VTH−1V∑VT. Then, find the smallest eigenvalue and its eigenvector C. Finally, we obtain G = (V∑VT)−1C. In the singular case where the smallest positive singular value of X is less than a small-valued tolerance, G is just the right eigenvector of the smallest singular value. This method is summarized in Fig. 9.

Figure 9
figure 9

Pratt method: (a) Gathered data points and (b) Flowchart.

Full size image

The above circumcenter method and the Pratt method are non-iterative fitting method. Thus, they prefer largely distributed arcs data in the beginning of the calculation procedure. The QFG radar is adequate for providing such lengthy arcs with only a small displacement. On the other hand, the QCW radar having a short arc with a small displacement should use computationally complex fitting method such as geometric iterative fitting method. This kind of complex method is not recommended for the QFG radar, but is used in this paper for comparison of algorithms. In this paper the LM method is used for the comparison: the LM method is the most popular geometric fitting method38 and the detailed description can be found in Zakrzewski et al.5, Chernov et al.28, and Gander et al.38.

Results

Simulation Results

In the simulations, the center estimation performance is mainly discussed. To do this, we first define a normalized estimation error, the similar definition is used in Gao et al.21:

$$Error=\frac{\Vert (D{C}_{I},D{C}_{Q})-({\widehat{DC}}_{I},{\widehat{DC}}_{Q})\Vert }{R}\times 100\,( \% ),$$
(23)

where (DCI, DCQ) is the real DC-offset, R is the radius of the real circle, and \(({\widehat{DC}}_{I},{\widehat{DC}}_{Q})\) is the estimated DC-offset. First, we compare the QFG radar and QCW radar the following parameter settings; Δf = 20 MHz and M = 3. Target is located at d = 30 cm, its movement is assumed to be sinusoidal displacement with Δx = 1 mm, and the baseband SNR is set to 40 dB. The real DC-offset is (DCI, DCQ) = (1, 1). After the IQ-imbalance correction as described in previous section, the baseband signals of the QFG radar are shown in Fig. 10 for four different bands fc = 400 MHz, 2.4 GHz, 10 GHz, 24 GHz. In the four complex planes in Fig. 10, star marks indicate the estimated DC-offset \(({\widehat{DC}}_{I},{\widehat{DC}}_{Q})\); three estimation results of circumcenter, Pratt, and LM methods are placed as star marks in each complex plane. We define the arc possession in percentage as the total arc distribution over one wavelength. For the QCW radar, the arc possession for the four bands in Fig. 10 are 0.13%, 0.8%, 3.3%, and 8%, respectively. The QFG radar extends the arc possession to 27.5%, 31.5%, 46.7%, and 42.7% of the corresponding fc although some extensions are discontinuous. This difference about the arc possession has a direct impact on the center estimation performance of the two radars. Figure 11 compares the normalized error of the QFG radar with QCW radar using the circumcenter method. Figure 11 shows that the error is reduced by the arc extension regardless of the arc continuity. The QCW radar shows significant performance degradation for all fc, but the QFG radar has much better performance. For fc ≥ 2.4 GHz, the error of the QFG radar is less than 3%.

Figure 10
figure 10

Arcs of the QFG radar for different fc (Real center of the arcs are C (1, 1)): (a) fc = 400 MHz (b) fc = 2.4 GHz (c) fc = 10 GHz, and (d) fc = 24 GHz.

Full size image
Figure 11
figure 11

Normalized error for different carrier frequency bands for Δf = 20 MHz: (a) the QFG radar and (b) the QCW radar.

Full size image

Matlab R2017a is used for these simulations. 100 times of experiments are performed and calculated the average for each simulation. The following simulation shows how the normalized error is affected by SNR. It can be said that the higher fc, more sensitive the radar is to SNR. For fc = 24 GHz, the normalized error for SNR from 12 dB to 50 dB is shown in Fig. 12, in which the circumcenter method is used. To obtain the error less than 10%, at least SNR should be 21 dB. Figure 13 shows that the error is slightly lowered by using the Pratt and LM methods. The pure white and black bars indicate the errors for SNR = 10 dB and 50 dB, respectively. At high SNR, the LM method is similar error rate to the Pratt method. On the other hand, at low SNR, the Pratt method is slightly better than the LM method.

Figure 12
figure 12

The effect of SNR on the error performance of circumcenter method.

Full size image
Figure 13
figure 13

Performance comparison of three estimation methods according to SNR (Note:Arc possession is 42.7%).

Full size image

In practice, smaller Δf is preferred because the phase-locked loop (PLL), which is the frequency changing device, is fast and more stable for small frequency change. The reduced arc possession due to the small Δf can be increased by large M. Thus, Δf and M is a design factor when a hardware specification is given. For example, when Δf = 3 MHz, Δx = 0.5 mm, and M = 4, the arc possessions of the QFG radar for above the four fcs are about 20%, where the arcs for fc = 24 GHz is depicted in Fig. 14(a). In this case, the normalized error performance of the circumcenter method at SNR=30 dB is as depicted in Fig. 14(b). Compared with Fig. 10, reduced arc possession due to some overlapped sections affects the center estimation performance. When preferring small Δf, M is required to be properly set according to Δf and Δx.

Figure 14
figure 14

The QFG radar for Δf = 3 MHz: (a) arcs and (b) normalized error for different carrier frequency bands.

Full size image

Experimental Results

The feasibility of the proposed QFG radar is experimentally evaluated in the measurement setup as shown in Fig. 15. The transceiver of the SFCW-type radar is an Infineon BGT24LTR operating at 24 GHz with an output power of 1 dBm. The PLL is a Texas Instrument LMX2491, and the I/Q amplifier is a Texas Instrument INA827 of which gain is 7 dB. Antenna has 5 dBi gain and 43° half-power beamwidth, which is placed 15 cm away from the target. The mechanical stage is used to create displacement of 0.5 mm. The target having uneven surface is mounted on the stage. Its height and width are 35 cm and 25 cm. The unevenness is good for making environmental impairment easily. The cables between the radar and antenna are Pasternack PE350, of which each length is 2 m and dielectric constant is 2.30. The PC acquires the received signals I and Q through a Labjack T7-Pro DAQ. Matlab R2017a is used for controlling the radar, running center estimation algorithms, and adding white Gaussian noise. For experiments, we have three frequency groups \({{\rm{F}}}_{1},{{\rm{F}}}_{2},\,{\rm{and}}\,{{\rm{F}}}_{3}\) according to Δf = 1 MHz, 2 MHz, and 3 MHz, respectively. Each frequency group has four frequency elements and their fc is 24.000 GHz. In the first experiment, we compared the equations about arc length (16) and arc interval (14) with the experiment results at the high SNR = 50 dB. The IQ-imbalance was corrected using (3), and The Pratt method was used to estimate the DC-offset. Figure 16 shows the resultant arcs of the QFG radar in this experiment, where four arcs are displayed in each chart and the radius of the arcs are 0.808. The measured arc length and interval values are summarized in Table 1, in which the average values are almost same as equations (16) and (14). As discussed earlier in previous section, the arc interval is reduced when Δf is small. One thing to note here is that the cable helps to increase the arc interval when the distance between the radar and the target is closely placed. Actually, when Δf = 1 MHz the cables themselves increase the arc interval by about 7.3 degrees. The total arc possession of this experiment is summarized in Table 2(a). The QFG radar gives the arc possession of 20.2% at Δf = 3 MHz compared to only 5.1% for the QCW radar, and their normalized center estimation errors are summarized in Table 2(b). The performance of the QFG radar at Δf = 3 MHz is experimented over SNR from 15 dB. Fitted circles on some SNRs are depicted in Fig. 17. As SNR is decreased, the deviation from the ground truth circle is increased for the three fitting algorithms. Performance of the normalized center estimation error for all SNR ranges are shown in Fig. 18. For sufficiently high SNR, SNR > 30 dB in this experiment, the three algorithms showed feasible results. The Pratt and LM methods were shown to be feasible in all SNR ranges. Thus, when the available SNR is known, the appropriate fitting algorithm can be selected. After performing the center estimation, it is easy to calculate the displacement. For Δf = 3 MHz and SNR = 30 dB, the calculations for Δx = 0.3 mm, 0.5 mm, 1 mm are performed and shown in Table 3, where 50 vibrations are measured and averaged for each Δx. The relative errors of the displacement calculation are 2.3%, 1.4%, and 0.8%, respectively. These results are comparable with the results using CW Doppler radar39, where the results39 used the pre-calibration step to get the DC-offset using sufficiently long arc while the QFG radar uses no pre-calibration step.

Figure 15
figure 15

(a) Measurement setup (b) Photograph (c) The SFCW-type radar system.

Full size image
Figure 16
figure 16

Arcs of the QFG radar in the experiment. Red, green, blue, and yellow arcs are for four frequencies elements. The dashed circle with the center at (0, 0) is the ground truth.

Full size image
Table 1 Arc length and interval values in the experiment shown in Fig. 16.
Full size table
Table 2 (a) Arc Possession of the experiment shown in Fig. 16, (b) Normalized Erro.
Full size table
Figure 17
figure 17

Fitting results on noisy dataset for three algorithms. Red dotted circle is the ground truth and the black dashed circle is the fitted result. (Note:Arc possession is 20.2%).

Full size image
Figure 18
figure 18

Performance comparison of three estimation methods for the QFG radar over various SNRs (Note:Arc possession is 20.2%).

Full size image
Table 3 Comparison of displacement measurement accuracy (QFG radar: Δf = 3 MHz, and SNR = 30 dB, CW radar: SNR is not mentioned in39 but it can be assumed that the SNR is sufficiently high SNR enough)).
Full size table

Simulation and experiment results show that the circumcenter method has inferior performance compared to the Pratt and LM methods, especially for low SNRs, because the circumcenter method estimates the center by using only three points S among the available data points, whereas the other two methods use all the data points. However, for high SNRs, the circumcenter method is advantageous compared to the other methods because the circumcenter method is computationally simple. In this paper, we consider the time required for MATLAB to compute the center estimation methods by using the profile function in MATLAB, where MATLAB was run on the Intel i7-7500U processor at the clock frequency 2.7 GHz. For various SNRs, the execution times of the methods are shown in Table 4, in which each time value refers to one execution time. The execution times are measured with 100 iterations and averaged for each simulation. For each method, 40 complex data points were put. For LM method, iteration threshold was set to 10−6, and the maximum iteration number was limited to 50. The circumcenter method has the smallest computation time of around 0.16 ms. The Pratt and LM methods require twice and four times the amount of computation time that the circumcenter method does, respectively. For the LM method, the lower the SNR, the longer the computation time because the number of iterations increases.

Table 4 Computational complexity.
Full size table

Discussion

The micro-Doppler radar is a promising technique for small vibrational displacement such as non-contact vital signal sensing. It can be used as sleep monitoring, driver drowsiness/fatigue detection, buried survivor searching, and other human motion classifying applications. The QFG radar is useful for estimating the center of a circle where enough arcs are hard to be obtained. The QFG effectively extends arc length with such a small displacement which helps improving the performance of the abovementioned center estimation algorithms. Some simulation results have been shown for various carrier frequency bands with different Δf, and M. Experimental results have been shown using 24 GHz SFCW-type radar system with the target of 0.5 mm displacement. Both of the simulation and experimental results have shown that the QFG radar outperforms the QCW radar. Of course, the parameters of the QFG have to be properly designed for the given environment, which was discussed through some simulations. The QFG radar can serve as a DC-offset tracking method for real-time applications under the uncontrollable environment because the arc is sufficiently provided and the curve fitting algorithms can be implemented using the off-the-shelf embedded processors.