Main

The stability of magnetic skyrmions in B20-type crystals results from competition between Heisenberg exchange and chiral Dzyaloshinskii–Moriya interaction (DMI)4,5. Since cubic anisotropy in such crystals is typically negligibly small and, to a first approximation, Heisenberg exchange and DMI are assumed to be isotropic, it is common to refer to them as isotropic chiral magnets. In such systems, DMI is predicted to favour skyrmion solutions of fixed chirality6, in agreement with experimental observations7,8,9,10.

Skyrmions in isotropic chiral magnets typically take the form of vortex-like tubes or strings, which penetrate through the entire sample thickness. As a result of conical modulations, a cross section of an isolated skyrmion tube resembles a two-dimensional (2D) skyrmion in a tilted ferromagnetic vacuum11. Recent theoretical studies3,12 of a 2D model of an isotropic chiral magnet have revealed many intriguing effects. In particular, it was shown that there is a stable solution for a skyrmion antiparticle—an antiskyrmion—which is characterized by opposite chirality in different spatial directions3.

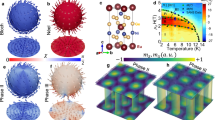
We begin by checking the stability of such a solution for a film of finite thickness with a three-dimensional (3D) model, taking into account demagnetizing fields. Figure 1a illustrates statically stable solutions for a skyrmion, an antiskyrmion, a skyrmionium and a representative skyrmion–antiskyrmion pair obtained by micromagnetic calculations (Methods and Extended Data Fig. 1a,b) (for illustrative purposes, the different spin textures are combined in a single simulated domain in an optimal field at which all of them are stable). The 3D spin textures are visualized by means of isosurfaces and a standard colour code for spin directions. It is important to note that the isolated antiskyrmion and skyrmion–antiskyrmion pair (Fig. 1) are statically stable states and are therefore fundamentally different from the dynamic antiskyrmions that have been discussed earlier13,14,15.

Fig. 1: Different localized magnetic states in a thin plate of a chiral magnet.
figure 1

a, Micromagnetic simulation of a plate of thickness t = 50 nm of an isotropic chiral magnet that supports a skyrmion, an antiskyrmion, a skyrmion–antiskyrmion pair and a skyrmionium in a perpendicular magnetic field. The lateral size of the simulated domain is 512 × 512 nm2. The mesh size is 256 nodes × 256 nodes × 65 nodes. Periodic boundary conditions are applied in the x–y plane. The spin textures are visualized in the form of isosurfaces where mz = 0. The lower image shows an over-focused Lorentz TEM image calculated for the above spin texture for an electron beam that is parallel to the z axis. b, Sections of the spin textures in a at z = 0 (bottom), z = t/2 (middle) and z = t (top). The direction of magnetization is shown using a standard colour code: black and white denote up and down spins, respectively, whereas red, green and blue denote the azimuthal angle. c–e, Under-focused (c) and over-focused (d) Lorentz TEM images calculated for defocus distances of 800 μm and the corresponding calculated electron holographic phase-shift image (e).

Full size image

The colour variation at the edges of the simulation box indicates the presence of a conical spiral in the direction of external magnetic field Bext ∥ ez. The period of cone modulations, that is, \({L}_{{{{\rm{D}}}}}=4\uppi {{{\mathcal{A}}}}/{{{\mathcal{D}}}}\), depends on the ratio between exchange stiffness constant \({{{\mathcal{A}}}}\) and DMI constant \({{{\mathcal{D}}}}\). It, therefore, varies between different compounds. For example, in FeGe, LD = 70 nm. As a result of the presence of conical modulations, demagnetizing fields and chiral surface twist, the spin texture notably changes through the film thickness (Fig. 1b). Figure 1c–e shows the simulations of Lorentz transmission electron microscopy (TEM) images and an electron holographic phase-shift image. Supplementary Fig. 1 shows a series of Lorentz TEM images simulated for different defocus distances.

Following a general approach for the classification of solutions in systems in which the order parameter is the unit-vector field, the localized magnetic textures (Fig. 1) can be classified based on the topological index as

$$Q=\frac{1}{4\uppi }\int {{{\bf{m}}}}\cdot \left({\partial }_{x}{{{\bf{m}}}}\times {\partial }_{y}{{{\bf{m}}}}\right){{{\rm{d}}}}x{{{\rm{d}}}}y\,,$$
(1)

where m(r) is the magnetization unit-vector field. Since the magnetic texture (Fig. 1) is smooth and free of Bloch points, the above definition of Q is valid in any arbitrarily chosen x–y plane. The total topological index of the combined spin texture (Fig. 1) is zero, since the topological indices of a skyrmion and antiskyrmion are −1 and +1, respectively, whereas the topological index of a skyrmionium is zero.

In our micromagnetic simulations, the isolated skyrmion and antiskyrmion remain stable over a wide range of fields, whereas in the pure 2D case, the isolated antiskyrmion stability range is very narrow3. The wide range of antiskyrmion stability in the 3D case can be explained by the gain in DMI energy due to chiral modulations across the plate thickness (Extended Data Fig. 1c,d). The stability of 3D antiskyrmions is also supported by Monte Carlo simulations performed at finite temperatures (Supplementary Video 1) and stochastic Landau–Lifshitz–Gilbert simulations (Supplementary Data 1). In contrast, the skyrmion–antiskyrmion pair (Fig. 1) has weaker stability and annihilates with increasing magnetic field or under the influence of weak perturbations (Supplementary Figs. 2 and 3 and Supplementary Video 2 show details of pair nucleation and annihilation processes). Since skyrmion–antiskyrmion pair annihilation can be triggered in different ways depending on their mutual orientation and environment, strictly speaking, there are no exact critical fields bounding the stability of the skyrmion–antiskyrmion pair. Such behaviour of the skyrmion–antiskyrmion pair is consistent with the prediction of the 2D model, suggesting that on a qualitative level, a 2D model of a chiral magnet is able to capture the main features of a more advanced 3D model. For instance, similar to the 2D case3, the 3D skyrmion–antiskyrmion pair has a few mutual orientations of the skyrmion and antiskyrmion at which they remain stable (Extended Data Fig. 3e shows another stable skyrmion–antiskyrmion pair orientation). The asymmetric interaction potential between the skyrmion and antiskyrmion and the different stability ranges are the fundamental properties that distinguish them from ordinary particles and antiparticles. Below, we provide experimental images of such pairs and compare them with micromagnetic simulations. In particular, we present experimental results on the creation and annihilation of a skyrmion–antiskyrmion pair, which are guided by a different theoretical prediction of a 2D model, which shows that a set of closed domain walls, such as a skyrmion bag, can decay into ‘elementary’ particles—skyrmions and antiskyrmions—in a certain external magnetic field. This decay conserves the total topological index and thus represents a homotopic transition. Extended Data Fig. 2 illustrates such a decay induced by a tilted magnetic field for a skyrmion bag with Q = 1 and skyrmionium with Q = 0 for the 2D model. We find that in a 3D model of a sample with finite thickness, this instability occurs even in a perpendicular applied field.

Micromagnetic simulations of this process in a film of finite thickness in the presence of a demagnetizing field are provided in Extended Data Fig. 3 and Supplementary Fig. 3. Starting with a complex magnetic configuration in zero field, we observe the same qualitative evolution with an applied field as for the 2D case, eventually leading to the formation of skyrmions and antiskyrmions.

To perform experimental observations of the theoretically predicted phenomena, a thin plate was prepared from a single crystal of B20-type FeGe using a focused-ion-beam workstation and a lift-out method16. As shown in the scanning electron microscopy images (Extended Data Fig. 4) as well as the Lorentz TEM images presented below, the sample is defect free and has nearly the same thickness over the whole area. The nominal thickness of the square plate t is comparable to the size of chiral modulations LD (70 nm) in this compound. It should be noted that such an exceptionally thin and uniform film of a B20-type chiral magnet has not been studied before, to the best of our knowledge, using Lorentz TEM or other microscopy techniques. Taking into account possible errors in the thickness estimation of ~5 nm and the likely presence of a thin damaged surface layer of ~5 nm due to sample preparation17, it is reasonable to assume that the true magnetic thickness of the FeGe plate is ~50 nm.

Figure 2 shows representative experimental over-focused Lorentz TEM images of a square 1 μm × 1 μm plate of the FeGe sample recorded after distinct cycles of applied external fields. Figure 2a shows a representative ground state of the system in zero field, whereas Fig. 2b–f shows the typical contrast in an external magnetic field of above 200 mT applied perpendicular to the plate. Further experimental images are provided in Extended Data Fig. 6. Note that the pairs shown in Fig. 2c,e are prior states to the skyrmion–antiskyrmion pair depicted in Fig. 1. Theoretical Lorentz TEM images obtained using micromagnetic simulations for skyrmion–antiskyrmion pair nucleation are shown in Extended Data Fig. 3. Excellent agreement is obtained between the theoretical (Fig. 1 and Extended Data Fig. 3) and experimental (Fig. 2) Lorentz TEM images, confirming the formation of the four distinct states shown in Fig. 1. In the over-focused regime, an ordinary skyrmion is imaged as a bright circular spot, whereas an antiskyrmion is imaged as an elongated dark spot with weak bright contrast on only one side. The magnetic contrast of an antiskyrmion in our isotropic case differs from that of an antiskyrmion in a system with anisotropic DMI18,19, as a result of the asymmetry of antiskyrmions and additional modulations through the film thickness. The situation is different for Heusler materials18,19, in which antiskyrmions have a fixed orientation to the crystallographic axes. In contrast, in isotropic chiral magnets, an antiskyrmion has an additional rotational degree of freedom. Antiskyrmions with different orientations are shown in Fig. 2b–f. Since the antiskyrmion orientation is coupled to the in-plane components of the external field and remanent magnetization, all the antiskyrmions in the sample are identically oriented (Extended Data Fig. 3e,f). A skyrmionium is imaged as a bright circular halo surrounding a dark spot, whereas a skyrmion–antiskyrmion pair (Fig. 2b,c,e) shows a superposition of skyrmion and antiskyrmion contrast. The TEM images allow a skyrmionium and a skyrmion–antiskyrmion pair (Fig. 2c) to be distinguished despite their topological equivalence. Extended Data Fig. 7 shows the representative under-focused and over-focused Lorentz TEM images as well as the phase-shift images recorded using off-axis electron holography. The comparison between theoretical and experimental phase-shift images shows good quantitative agreement. Supplementary Fig. 6 shows the experimental images of antiskyrmions recorded at different specimen temperatures.

Fig. 2: Experimental Lorentz TEM images and diagram of observable states in a thin FeGe sample.
figure 2

a–f, Representative over-focused Lorentz TEM images in a square 1 μm × 1 μm FeGe sample with a nominal thickness of 70 nm recorded at T = 95 K. a is a representative example of a ground state with helical spirals. b–f are representative images arranged in the order of increasing magnitude of external magnetic field, demonstrating the coexistence of skyrmions and antiskyrmions. b shows a stable skyrmion–antiskyrmion pair. A series of defocused Lorentz TEM images of this state is shown in Extended Data Fig. 5. c shows one skyrmionium, one skyrmion–antiskyrmion pair, two antiskyrmions at the lower edge and four skyrmions at the right edge. d shows two skyrmions and two antiskyrmions separated by a large distance. e shows five antiskyrmions and one skyrmion–antiskyrmion pair. f shows three antiskyrmions and two skyrmions. g, Temperature–field diagram of states observed with an increasing external magnetic field. The red and magenta squares indicate the collapse fields of skyrmions and antiskyrmions, respectively. The antiskyrmion collapse field is extrapolated towards T = 0 K based on micromagnetic estimations. The hatched region indicates the presence of helical spirals, which transform into surface modulations at higher fields, as shown in c, in the form of weak contrast features whose periodicity is larger than that of helical spiral LD. The vertical dashed line at Tc = 287 K marks the Curie temperature of FeGe. Ta is the activation temperature, above which a skyrmion lattice spontaneously emerges in the red-shaded region (Supplementary Fig. 4). The symbols correspond to experimentally measured values, whereas the lines are guides to the eye. The error bars in our measurements are ~2 mT (0.1% of the objective lens current) and comparable with the size of the symbols.

Full size image

Figure 2g shows the experimentally estimated collapse fields of skyrmions and antiskyrmions as a function of temperature. The trend line of the experimental points for the antiskyrmion collapse field, extrapolated to zero temperature, shows reasonable agreement with the value of ~400 mT provided by micromagnetic simulations (Supplementary Fig. 2). At a magnetic field of ~200 mT (blue circles), weak contrast associated with surface-induced modulations20,21,22 emerges. This contrast transforms into helical spirals when the field is reduced, making it difficult to estimate the lower bound field for antiskyrmion stability, which is indicated by a blurred lower edge of the magenta region (Fig. 2g).

The experimental images shown in Fig. 2 and Extended Data Figs. 6 and 7 were obtained by using the following approach, which allows the observed magnetic states to be reproducibly generated. First, a perpendicular field of Bext ≈ 50 mT was cycled several times until a pattern of closed domain walls was observed, similar to that shown in Fig. 3a, in which the contour lines marked in white, red and yellow follow 180° domain walls. As a result of the presence of Fresnel fringes from the sample edges, the yellow contours near the left, right and lower edges of the sample only become evident with increasing field (Fig. 3b–e). The white and yellow contours enclose areas in which the magnetization is opposite to Bext, whereas the red contours enclose areas in which the magnetization is along Bext. In Fig. 3, the external magnetic field points towards the reader.

Fig. 3: Protocol for antiskyrmion nucleation and skyrmion–antiskyrmion pair production.
figure 3

a–l, Sequence of over-focused Lorentz TEM images recorded as a function of increasing external magnetic field Bext ∥ ez. The initial configuration in the zero field in a is identical to Fig. 2a. The white, red and yellow lines mark contours of 180° domain walls. The red and white contours form closed loops, whereas the yellow contours are discontinuous. With an increasing field, the white and yellow contours converge to form skyrmions, whereas the red contours converge to form antiskyrmions. After the annihilation of skyrmions and antiskyrmions marked by white and red dashed circles, respectively (g and h), the system converges to six antiskyrmions (i and j). On increasing the field further, the antiskyrmions collapse at Bext > 276 mT.

Full size image

When the external magnetic field is increased, the white contours converge to form skyrmions, whereas the red contours converge to form antiskyrmions (Fig. 3a). The larger the number of red contours present in the initial state, the more antiskyrmions are observed with increasing field, and vice versa. Extended Data Figs. 8 and 10 illustrate antiskyrmion nucleation for different initial states. If the helical modulations in the initial state do not form closed loops, then either only skyrmions or no skyrmions are observed with increasing field. The outer domain walls (Fig. 3a, yellow) typically do not form closed loops and are instead often connected to the sample edges. For example, eight stripes are connected to the upper edge of the sample (Fig. 3a). Our observations show that such stripes may give rise to an arbitrary number of skyrmions. In the present case (Fig. 3), these stripes continuously disappear (Fig. 3g) and the outer domain wall converges to form a single skyrmion. This process can be followed based on the total number of antiskyrmions present at higher magnetic fields (Fig. 3i,j). At intermediate fields, annihilation of skyrmion–antiskyrmion pairs is observed (Fig. 3g,h and Extended Data Figs. 8–10). Representative examples of individual skyrmion–antiskyrmion pair annihilation are presented in Fig. 4.

Fig. 4: Skyrmion–antiskyrmion pair annihilation.
figure 4

a,b, Over-focused Lorentz TEM images recorded before (a) and after (b) skyrmion–antiskyrmion pair annihilation induced by increasing the external field. The position of the pair is marked by dashed contours. A complete series of Lorentz TEM images showing in-field evolution for the states in a and b is provided in Extended Data Figs. 8 and 10, respectively.

Full size image

The weaker stability of skyrmion–antiskyrmion pairs is in good agreement with micromagnetic simulations (Supplementary Fig. 2). Furthermore, theoretical calculations suggest that the particle–antiparticle pair illustrated in Fig. 1 is statically stable only above a critical film thickness, which we estimate for FeGe to be 40 ± 5 nm. In a thinner film, such pairs annihilate immediately, similar to the behaviour for the 2D model (Extended Data Fig. 2). Direct observation of the annihilation process using TEM demands ultrafast imaging with at least nanosecond temporal resolution23.

Despite the topological equivalence between a skyrmion–antiskyrmion pair and a skyrmionium, we did not experimentally observe the transition between the two states. However, micromagnetic simulations suggest that such a transition can be achieved by slightly tilting the magnetic field by several degrees. In contrast to the formation of skyrmion–antiskyrmion pairs, the appearance of a skyrmionium in our experiments was a very rare event. The protocol (recently proposed elsewhere24) provides a reliable approach for the nucleation of a skyrmionium and other skyrmions with topological charge Q ≥ 0.

It should be noted that the approach described above for antiskyrmion nucleation is only applicable for thin plates, for which t ≲ LD. As reported in many earlier works, in thick plates of cubic chiral magnets, irrespective of their initial state, the system usually only converges to an energetically more favourable state that contains skyrmions. An alternative approach for the creation of antiskyrmions in thick plates will be presented elsewhere.

In conclusion, we have observed the creation and annihilation of skyrmion antiparticles in an isotropic chiral magnet—B20-type FeGe. Micromagnetic simulations support these observations and show excellent agreement with the experimental data. The experimental observation of skyrmion–antiskyrmion pairs in an FeGe plate whose thickness is below the size of characteristic chiral modulation may serve as a platform to study the fundamental physics of topological solitons in magnetic solids. The good qualitative agreement of the observed phenomena with theoretical predictions for a 2D model3 suggests that a large diversity of other phenomena predicted by this model25,26,27 may be experimentally verified in thin films of cubic chiral magnets. Our results suggest that a thin plate of an isotropic chiral magnet may provide a platform for the experimental verification of the effect of a sign change in a topological Hall signal when the system contains antiskyrmions instead of skyrmions28. Moreover, they open a wide vista for the experimental study of intriguing phenomena that manifest themselves as additional contributions to a Hall signal, even when the averaged topological density is zero (examples shown elsewhere29,30) for an identical number of particles and antiparticles.

Methods

Micromagnetic calculations

The micromagnetic approach was followed in this work. The total energy of the system includes the exchange energy, DMI energy, Zeeman energy and self-energy of the demagnetizing field31:

$$\begin{array}{ll}{{{\mathcal{E}}}}\,=\,\int _{{V}_{{{{\rm{m}}}}}}{\mathrm{d}}{{{\bf{r}}}}\,&{{{\mathcal{A}}}}\mathop{\sum}\limits_{i=x,y,z}| \nabla {m}_{i}{| }^{2}+{{{\mathcal{D}}}}\,{{{\bf{m}}}}\,\cdot (\nabla \,\times \,{{{\bf{m}}}})-{M}_{{{{\rm{s}}}}}\,{{{\bf{m}}}}\,\cdot \,{{{\bf{B}}}}+\\ &+\frac{1}{2{\mu }_{0}}\int _{{{\mathbb{R}}}^{3}}{\mathrm{d}}{{{\bf{r}}}}\,\mathop{\sum}\limits_{i=x,y,z}| \nabla {A}_{{{{\rm{d}}}},i}{| }^{2}\,,\end{array}$$
(2)

where the magnetic field is

$${{{\bf{B}}}}={{{{\bf{B}}}}}_{{{{\rm{ext}}}}}+\nabla \,\times \,{{{{\bf{A}}}}}_{{{{\rm{d}}}}}\,,$$
(3)

m(r) = M(r)/Ms is a unit-vector field that defines the direction of magnetization, Ms = ∣M(r)∣ is the saturation magnetization, Ad(r) is the component of magnetic vector potential induced by the magnetization, \({{{\mathcal{A}}}}\) is the exchange stiffness constant, \({{{\mathcal{D}}}}\) is the constant of isotropic bulk DMI and μ0 is the vacuum permeability (μ0 ≈ 1.256 μN A−2). In our simulations, we used the following material parameters for FeGe (ref. 32): \({{{\mathcal{A}}}}\) = 4.75 pJ m−1, \({{{\mathcal{D}}}}\) = 0.853 mJ m−2 and Ms = 384 kA m−1. These parameters provide the period of helical modulations at zero field, that is, \({L}_{{{{\rm{D}}}}}=4\uppi {{{\mathcal{A}}}}/{{{\mathcal{D}}}}\) = 70 nm, and the saturation field for the cone phase, that is, Bc = BD + μ0Ms = 0.682 T, where \({B}_{{{{\rm{D}}}}}={{{\mathcal{D}}}}/(2{M}_{{{{\rm{s}}}}}{{{\mathcal{A}}}})\) = 0.199 T. Details of the critical field are provided in another work33. The solutions of the Hamiltonian in equation (2) were found by using the numerical energy minimization method33 using the Excalibur software34. The termination criterion for convergence was chosen according to the Gill–Murray–Wright method35,36 with a function tolerance τF = 10−10.

Initial guesses for calculating antiparticles

Defining angle ϕA = πz/LD, the orientation of an antiskyrmion is first set in every z section in the form:

$$\left(\begin{array}{l}{x}^{\prime}\\ {y}^{\prime}\end{array}\right)=\frac{1}{l}\left(\begin{array}{ll}\cos {\phi }_{{{{\rm{A}}}}}&\sin {\phi }_{{{{\rm{A}}}}}\\ -\sin {\phi }_{{{{\rm{A}}}}}&\cos {\phi }_{{{{\rm{A}}}}}\end{array}\right)\left(\begin{array}{l}x\\ y\end{array}\right).$$
(4)

Following the approach introduced elsewhere12, the auxiliary vector field is defined according to the expression

$${{{{\boldsymbol{m}}}}}^{\prime}=\frac{1}{{g}_{+}}{\left(2{x}^{\prime}-{y}^{\prime},{x}^{\prime}-2{y}^{\prime},{g}_{-}\right)}^{{{{\rm{T}}}}},$$
(5)

where \({g}_{\pm }=\frac{5}{4}\left({\left({x}^{\prime}\right)}^{2}+{\left({y}^{\prime}\right)}^{2}\right)-2{x}^{\prime}{y}^{\prime}\pm 1\) and scaling parameter l defines the antiskyrmion size. In our simulations, we let l = 0.25LD. For an antiskyrmion embedded in a ferromagnetic background, we use the following initial guess:

$${{{\boldsymbol{m}}}}={R}_{{{{{z}}}}}({\phi }_{{{{\rm{A}}}}}){{{{\boldsymbol{m}}}}}^{\prime}\,,$$
(6)

where Rz(ϕA) is a 3 × 3 rotational matrix about the z axis. For an antiskyrmion embedded in the conical phase, the initial guess takes the form

$${{{\bf{m}}}}={R}_{{{{{z}}}}}({\phi }_{{{{\rm{c}}}}}){R}_{{{{{y}}}}}({\theta }_{{{{\rm{c}}}}}){R}_{{{{{z}}}}}({\phi }_{{{{\rm{A}}}}}-{\phi }_{{{{\rm{c}}}}}){{{{\bf{m}}}}}^{\prime},$$
(7)

where θc is the cone phase angle and ϕc = 2πz/LD.

An alternative approach for the construction of the initial state for an antiskyrmion is illustrated in Extended Data Fig. 1. This approach has been verified using the Mumax37 software.

Magnetic imaging using TEM

Fresnel defocus Lorentz TEM imaging and off-axis electron holography were performed using an FEI Titan 60-300 TEM instrument operated at 300 kV. The microscope was operated in aberration-corrected Lorentz mode with the sample in magnetic-field-free conditions. A conventional microscope objective lens was then used to apply out-of-plane magnetic fields to the sample, ranging between –0.15 and +1.50 T (precalibrated using a Hall probe). A liquid-nitrogen-cooled specimen holder (Gatan model 636) was used to control the specimen temperature between 95 and 380 K. Images were recorded when the specimen temperature was 95 K, if not specified otherwise. Fresnel defocus Lorentz TEM images and off-axis electron holograms were recorded using a 4k × 4k Gatan K2 IS direct electron-counting detector. The defocus distance was ∣Δz∣ = 800 μm for all the images presented in the text, if not specified otherwise. Multiple off-axis electron holograms, each with a 4 s exposure time, were recorded to improve the signal-to-noise ratio and analysed using a standard fast Fourier transform algorithm in HoloWorks software (Gatan).

Theoretical Lorentz TEM and phase-shift images were calculated for numerical micromagnetic solutions by the method described elsewhere33 and implemented in the Excalibur software34.