Weak-coupling to strong-coupling quantum criticality crossover in a Kitaev quantum spin liquid α-RuCl₃

Abstract

We report a quantum criticality crossover representing two different universal scaling behaviors in a Kitaev quantum magnetic material α-RuCl₃. α-RuCl₃ presents both a symmetry-breaking antiferromagnetic order and a long-range entangled topological order of a quantum spin liquid, and thus could be a candidate system for a unique universality class involving deconfined fractionalized excitations of the local Z₂ fluxes and itinerant Majorana fermions. Theoretical analyses on the inelastic neutron scattering, ac-magnetic susceptibility, and specific heat results demonstrate that Wilson–Fisher-Yukawa-type ‘conventional’ weak-coupling quantum criticality in high-energy scales crosses over to heavy-fermion-type ‘local’ strong-coupling one in low-energy scales. Our findings provide deep insight on how quantum criticality evolves in fermion-boson coupled topological systems with different types of deconfined fermions.

Introduction

Searching for a universality class near a quantum-critical point (QCP), a precarious point of quantum instability between two competing phases, is a fundamental paradigm with the emergence of exotic elementary excitations. Quantum criticality involving quantum instability^1,2 has been demonstrated in various quantum systems with two competing orders such as magnetic heavy-fermion materials³, high-T_C superconductors⁴, one-dimensional Ising systems⁵, and Luttinger liquids^6,7. Meanwhile, topological orders with emerging gauge fields develop ground states without symmetry breaking as observed in fractional quantum Hall liquids^8,9 and quantum spin liquids (QSLs)^10,11, and the low-energy physics is described by deconfined fractionalized excitations. In particular, the topological QSL state is exactly derived by fractionalizing the spin excitations into localized Z₂ gauge fluxes and itinerant Majorana fermions (MFs) in a two-dimensional (2D) Kitaev honeycomb 1/2-spin network with Ising-like nearest-neighbor bond directional Kitaev exchange interactions¹². Recently, α-RuCl₃ has been found to host both the 2D Kitaev model with fractionalized excitations and a zigzag-type antiferromagnetic (AFM) order below T_N ≈ 6.5 K^13,14,15,16.

The Ru³⁺ ion in α-RuCl₃ has a J_eff = 1/2 pseudospin¹⁷ due to strong Ru 4d spin–orbit coupling, and the system becomes a spin–orbit-coupled Mott insulator¹⁵. The orbital state forms three orthogonal bonds in the honeycomb lattice to embody the Kitaev model in the edge-shared octahedral environments¹⁸. Indeed, magnetic susceptibility, specific heat, Raman spectroscopy, and neutron scattering measurements consistently demonstrate the characteristic behaviors of thermally fractionalized MFs above T_N, suggesting proximity to the Kitaev QSL phase competing with the AFM phase^19,20,21,22. The quantum nature of fractionalized MFs also reveals in the thermal Hall measurements. Although are still debates with sample dependence^23,24 or quantum oscillation of transverse thermal conductivity²⁵, half-integer quantization of thermal Hall conductivity emerges as the magnetic field becomes large enough to suppress the AFM order^26,27,28.

Meanwhile, the dynamic spin susceptibility, which agrees well with the pure Kitaev behavior in a high-energy scale (T or ω ≳ 5 meV), considerably deviates from the Kitaev behavior in a low-energy scale (T or ω ≲ 4 meV) above T_N²⁰. Such proximity behaviors may indicate that the system is nearby a QCP between competing topological QSL and long-range-ordered AFM phases and possibly offers a universality class relevant to the topological order.

In this study, we report a quantum criticality crossover in α-RuCl₃, which represents two different universal scaling behaviors in the low and high-energy scales. We demonstrate experimentally as well as theoretically that the low-energy spin dynamics obtained from the inelastic neutron scattering (INS) follows heavy-fermion-type strong-coupling physics, although the high-energy one follows weak-coupling physics close to the pure Kitaev. We also ensured that the strong-coupling local quantum criticality at low energies emerges from the weakly coupled rather conventional Wilson–Fisher-Yukawa-type quantum criticality at high energies. The crossover behavior is also confirmed in the magnetic-specific heat C_m, which displays a peculiar plateau up to ~50 K above T_N and then follows a T-linear increase to ~100 K, as well explained with the low-energy strong-coupling local critical physics and the high-energy weak-coupling itinerant Dirac fermion one.

Results

Physical picture

We first discuss a physical picture with respect to a universality class and quantum criticality for critical spin fluctuations in a model system with two competing interactions of 2D Kitaev and Ising-type AFM exchange interactions as in α-RuCl₃. The AFM spin fluctuations couple to two different types of deconfined fractional excitations of localized Z₂ fluxes and itinerant MFs dominantly in low- and high-energy scales, respectively.

At high temperatures far above T_N, the Z₂ fluxes and MFs dissolve to form an incoherent critical soup. The original quasiparticle weights become vanishing, and emerging excitations losing the quasiparticle nature specify characteristics of weak-coupling conventional quantum criticality. This phenomenon is analogous to the physics of metallic quantum criticality responsible for the marginal Fermi-liquid phenomenology in the strange metallic phase of high-T_C cuprates⁴, where the Landau quasiparticle excitations dissociate into incoherent particle-hole excitations due to their correlations. Remarkably, this conventional quantum criticality evolves into strong-coupling local quantum criticality at low temperatures above T_N, where critically fluctuating local moments appear to carry the entropy, analogously to the local quantum criticality of heavy-fermion systems³. This crossover behavior in quantum-critical physics of α-RuCl₃ originates from the coupling between the Ising-type AFM fluctuations and the two types of deconfined fractionalized fermions governing different energy scales.

Figure 1a shows a schematic-phase diagram representing the Kitaev QSL phase with the well-defined fractionalized excitations and the zigzag AFM phase, similar to the diagram of the Landau Fermi-liquid phase with well-defined quasiparticle excitations and an associated symmetry broken phase, respectively. Here the external tuning parameter, such as the magnetic field or pressure, tunes the ratio of the AFM exchange J to the QSL Kitaev exchange K. In a J = 0 limit, the spin-spin correlation is governed by K leading to the Kitaev QSL ground state. The spin excitations are fractionalized into itinerant MFs and gapped Z₂ fluxes, which become consecutively defined upon cooling through T_H and T_L, respectively^29,30.

Fig. 1: Schematic diagrams near the quantum-critical point.

a Schematic-phase diagram as a function r (J/K), a ratio of the non-Kitaev antiferromagnetic (AFM) exchange J to the Kitaev exchange K. The quantum-critical region is divided into a weak-coupling one in high temperatures (green-shaded) and a strong-coupling one in low temperatures (blue-shaded) governed by different critical scaling physics, resulting in a crossover behavior of the quantum criticality (QC). b Renormalization group (RG) flows on the r = r_C critical surface described with two coupling constants λ, g, and velocity v_flux of the Z₂ flux excitation. The RG flows at high temperatures (v_flux = c) show actual results of the Wilsonian RG analyses in the one-loop level, while those are schematically presented at low temperatures (v_flux = 0).

In the Kitaev paramagnetic (PM) phase (T_L < T < T_H), the MFs exhibit metallic behaviors under thermally fluctuating Z₂ fluxes. Below T_L, the Z₂ fluxes are frozen, and only low-energy MFs remain itinerant. Even for a finite J, the QSL ground state persists if r = J/K is sufficiently small. As r increases, the AFM coherence length (ξ) increases, while the coherence temperature T^* ~ ξ⁻¹ decreases. In a large r limit, the AFM long-range order (LRO) is stabilized below T_N due to the dominant J. The quantum phase transition between QSL and LRO phases is expected to occur at a moderate value of r = r_C (QCP), and the physical behaviors become quantum critical in the region (blue-shaded) around QCP. Considering that the magnetic field-induced AFM to QSL transition α-RuCl₃ occurs at H_C ~6 T (see Supplementary Fig. 3)²⁶, its r-value is expected to be near the critical point r_C as presented in the figure.

The most fascinating physics is an apparent crossover behavior across the high (green-shaded) to low-temperature (blue-shaded) region, suggesting the presence of two types of ω/T quantum-critical scaling physics in the dynamic spin susceptibility. This crossover behavior results from the fact that the spin excitations in high- and low-energy scales are governed by different fixed points (FPs) and there appears a renormalization group (RG) flow between these two FPs as a function of the energy scale parameter (T or ω). As a result, the fractionalized excitations form an intriguing QSL state in this quantum-critical region. Here the phase boundaries are based on experimental observations^20,21,22,26 and theories^29,30, although the diagram is rather schematic. The crossover region in Fig. 1a is referred to the neutron scattering (Fig. 2b) and magnetic-specific heat results (Fig. 8a).

Fig. 2: Temperature-dependent INS spectra of α-RuCl₃.

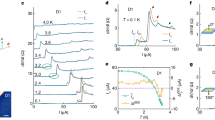
a Inelastic neutron scattering S(Q, ω) maps along high-symmetry directions as indicated in the HK-reciprocal space of the rhombohedral ($R\bar{3}$) structure. Each map presents combined two data sets with incident neutron energies of E_i = 50 meV (upper) and 22 meV (lower). b S(Q, ω) spectra at Q = Γ(0, 0, 0) measured at T = 25 K and 75 K in a log–log scale. Red dashed line is a linear guideline for a power-law behavior of the excitations above ~4 meV. Error bars represent 1 standard deviation.

Building upon the physical picture described in Fig. 1a, we explore the nature of this quantum criticality, where the critical AFM spin fluctuations couple to both Z₂ fluxes and MFs. Figure 1b displays the RG flow diagram around the critical surface at r = r_C. The RG flows in the high-energy scale show actual calculation results of the Wilsonian RG analyses conducted in the one-loop level on the critical surface. On the other hand, those are schematically presented in the low-energy scale, where the physics involves strong coupling between the deconfined excitations and AFM fluctuations to be beyond the perturbative framework. However, it is worth noting that the existence of the strong-coupling FP is verified by the dynamical mean-field theory (DMFT) calculation, as discussed below.

In the absence of fractionalized excitations, the Ising spin quantum criticality is represented with the Wilson–Fisher type FP³¹ characterized by an effective critical interaction λ between the Ising spin fluctuations. Meanwhile, as this spin sector interaction is turned off (λ = 0), the fractionalized fermionic spin excitations can be described in terms of an effective Yukawa-type theory characterized by an effective critical Yukawa coupling g between the fractionalized excitations and the spin fluctuations. This theory naturally hosts a weak-coupling FP³¹. When λ ≠ 0, an interacting FP, referred to as a Wilson–Fisher–Yukawa FP, emerges on the critical surface as presented in Fig. 1b (the high-temperature green-shaded region in Fig. 1a).

The proximity effect observed in α-RuCl₃ at high temperatures is expected to be governed by this interacting FP. The dynamic spin susceptibility should exhibit a universal behavior and further follow a universal scaling law characterized by an anomalous critical exponent derived from this FP. It is remarkable to note that this Wilson–Fisher–Yukawa FP becomes destabilized at low temperatures (T ≲ 4 meV) above T_N to flow into another FP, where the propagation velocity of the Z₂ flux excitation is strongly renormalized (localized Z₂ flux excitation). Then the nature of spin dynamics becomes locally critical (a strong-coupling FP) as described for the local quantum criticality of heavy-fermion physics. The appearance of the localized flux excitations in the Kitaev QSL state is likely responsible for the heavy-fermion type local quantum criticality in the low-energy scale.

Inelastic neutron scattering

The dynamic spin susceptibility can be extracted from INS measurements probing the magnetic excitations. The scattering cross-section is proportional to the dynamic structure factor S(Q, ω) of the spin correlation function, which displays the magnetic excitations in the transferred momentum (Q) and energy (ω) space. Figure 2a shows representative S(Q, ω) maps of α-RuCl₃ in the HK-reciprocal space measured at temperatures below (T = 2.3 K) and above T_N = 6.5 K (T = 25 K, 75 K, and 150 K). The S(Q, ω) map at T = 2.3 K exhibits a strongly dispersive feature of spin wave excitations originated from the zigzag AFM order below 4 meV. Besides the spin wave feature, it also displays broad continuum excitations extending from near 0meV to even above 15 meV through the whole Brillouin zone, which corresponds to the fractionalized MFs excited from the Kitaev QSL state^20,30. These continuum excitations emerge upon cooling across the fractionalization temperature (T_H ~ 100 K) and persist even below T_N, reflecting the proximity to the QSL²⁰.

Above T_N (25 K and 75 K), one can recognize distinguishable energy-dependent behaviors of the continuum excitation weight around Q = Γ(0, 0, 0) across ~4 meV; a strong spectral weight is nearly maintained up to ~4 meV and then become significantly reduced with the increase of the energy. Such energy-dependent behaviors can be clearly observable in the S(Q = Γ, ω) spectra in the log–log scale as shown in Fig. 2b. Above ~4 meV, the spectral intensity merges on a linear line representing a single scaling of criticality while it apparently deviates from the line below ~4 meV, alluding to the emergence of emergence of another scaling. This result is consistent with the weak-coupling to strong-coupling quantum criticality crossover as described above (also see Fig. 1) and suggests that the nature of continuum excitations can be characterized by two different universal scaling laws, i.e., one for the weak-coupling and the other for the strong-coupling quantum criticality in the high and low-energy scales, respectively. Interestingly, a puzzling plateau feature above T_N observed in the specific heat²⁰ persists up to 50 K, corresponding to the deviation energy scale (~4 meV). We speculate that the delocalized Z₂ flux excitations at high temperatures become localized below this temperature, although it is well above the freezing temperature T_L in the pure Kitaev^29,30, causing a heavy-fermion type local quantum criticality as discussed below.

Effective field theory

In this section, we introduce an effective field-theory modeling for the spin excitations of α-RuCl₃ with the AFM spin fluctuations coupling to the Z₂ fluxes and itinerant MFs in order to derive the universal scaling applicable to the dynamic spin susceptibility extracted from the INS results. The true magnetic lattice Hamiltonian of α-RuCl₃ is quite complicated and still under debate. Thus we build up a simplified Kitaev QSL interacting with the zigzag AFM order in the α-RuCl₃ lattice.

We first adopt a coarse-grained lattice model (Fig. 3a) to construct the effective Hamiltonian consisting of the Kitaev QSL Hamiltonian H_K, the zigzag AFM Ising spin Hamiltonian H_AF, and an effective Zeeman-type interaction V_K-AF accounting for a coupling between the Kitaev fermions and the zigzag AFM- ordered spins. The total Hamiltonian can be described as follows,

$$\begin{array}{lll} H&=&{H}_{{{{\rm{K}}}}}+{H}_{{{{\rm{AF}}}}}+{V}_{{{{\rm{K-AF}}}}},\\ {H}_{{{{\rm{K}}}}}&=&-\mathop{\sum}\limits_{\left\langle ij\right\rangle }{K}_{{\gamma }_{ij}}{\sigma }_{i}^{{\gamma }_{ij}}{\sigma }_{j}^{{\gamma }_{ij}},\,\,\,{V}_{{{{\rm{K-AF}}}}}=-g\mathop{\sum}\limits_{i}{\phi }_{i}{\sigma }_{i}^{z},\end{array}$$

(1)

where ${\sigma }_{i}^{\alpha }$, α = x, y, z are the Pauli matrices at honeycomb lattice site i, $\left\langle ij\right\rangle$ represent nearest-neighboring sites, γ_ij = x, y, z depending on the bond as shown in Fig. 3a, and ϕ_i is the zigzag AFM order parameter fluctuations. Here, we do not specify H_AF explicitly due to the lack of concensus on the lattice magnetic Hamiltonian. The detailed form of H_AF is not important in this study, only for the long-range physics. We will implement dynamics of the zigzag Ising AFM order in a continuum expression form when we construct the effective action below. The interaction V_K-AF between σ and ϕ is supposed to be in a local Zeeman type.

Fig. 3: Schematic descriptions of the theoretical model and quantum-critical scaling behaviors of dynamic spin susceptibility.

a Kitaev honeycomb lattice represented by two triangular sublattices differentiated by black and white dots and zigzag antiferromagnetic ordering. b Deformed brick-wall type lattice by stretching the honeycomb lattice along the zigzag chain. The red and yellow balls are f_r,b and f_r,w fermions, respectively. c Conceptual diagram for emergent local quantum criticality in the low-energy scale.

The zigzag AFM order consists of alternating spin chains with different spin states, and the original honeycomb lattice is identically represented by a brick-wall lattice. Under the Jordan–Wigner transformation for the spin variables described in Fig. 3b, one can map the Kitaev spin model to a fermionic model: Transforming the spin operators ${\sigma }_{i}^{\alpha }$ as

$${\sigma }_{i}^{z}={K}_{i},\,{\sigma }_{i}^{+}={f}_{i}^{{\dagger} }\mathop{\prod}\limits_{j < i}{K}_{j},\,{\sigma }_{i}^{-}=\left(\mathop{\prod}\limits_{j < i}{K}_{j}\right){f}_{i},$$

(2)

where ${K}_{i}=2{f}_{i}^{{\dagger} }{f}_{i}-1$, and f_i (${f}_{i}^{{\dagger} }$) are fermion annihilation (creation) operators. Then H_K becomes

$${H}_{{{{\rm{K}}}}}=-\mathop{\sum}\limits_{r,a=x,y}{K}_{a}({\psi }_{r+a}^{{\dagger} }-{\psi }_{r+a})({\psi }_{r}^{{\dagger} }+{\psi }_{r})-{K}_{z}\mathop{\sum}\limits_{r}(2{\chi }_{r}^{{\dagger} }{\chi }_{r}-1)(2{\psi }_{r}^{{\dagger} }{\psi }_{r}-1),$$

(3)

where the lattice site index i is separated into Bravais lattice index r and the basis b or w for the black or white site, respectively, as shown in Fig. 3. We also combine the fermions attached to two ends of the z-bond as ${\chi }_{r}={{{\rm{Re}}}}{f}_{r,w}-{{{\rm{i}}}}{{{\rm{Im}}}}{f}_{r,b}$, and ${\psi }_{r}={{{\rm{Im}}}}{f}_{r,w}+{{{\rm{i}}}}{{{\rm{Re}}}}{f}_{r,b}$. Now ψ_rs resemble the itinerant fermions in the one-dimensional p-wave superconductor model and χ_rs representing the Z₂ fluxes describe localized fermions interacting with ψ_r fermions^31,32.

Now we consider V_K-AF, the coupling between the Ising spin fluctuations and the Jordan–Wigner fermions in the critical region. In the coarse-grained representation, this coupling can be expressed as a Yukawa-type effective interaction, and the model Hamiltonian becomes an effective continuum field theory described in terms of two types of fermion excitations coupled with Ising spin fluctuations. The Yukawa-type effective interaction is given by

$${V}_{{{{\rm{K-AF}}}}}=-{{{\rm{i}}}}g\mathop{\sum}\limits_{r}{\phi }_{r}({\psi }_{r}^{{\dagger} }{\chi }_{r}^{{\dagger} }+{\psi }_{r}{\chi }_{r}).$$

(4)

To obtain the low-energy effective field theory, we expand both fermion fields near two gapless points for H_K in the momentum space. In the absence of zigzag AFM fluctuations (ϕ_r = 0), ${\chi }_{r}^{{\dagger} }{\chi }_{r}$ becomes a conserved quantity for each site r. The ground state sector is ${\chi }_{r}^{{\dagger} }{\chi }_{r}=0$, and within this sector, the Hamiltonian has gapless points at k = ± (4π/3, 0). Linearizing the Hamiltonian and using the field near these gapless points, we have

$${H}_{{{{\rm{K}}}}}=\mathop{\sum}\limits_{k}\mathop{\sum}\limits_{a=\pm }\left[{\epsilon }_{a,k}{\psi }_{a,k}^{{\dagger} }{\psi }_{a,k}+\frac{{{{\rm{i}}}}{{{\Delta }}}_{a,k}}{2}({\psi }_{a,k}^{{\dagger} }{\psi }_{-a,-k}^{{\dagger} }+{\psi }_{a,k}{\psi }_{-a,-k})+2K{\chi }_{a,k}^{{\dagger} }{\chi }_{a,k}\right]+{H}_{{{{\rm{int}}}}},$$

(5)

$${H}_{{{{\rm{int}}}}}=\frac{4K}{{N}_{z}}\mathop{\sum}\limits_{k,p,q}\mathop{\sum}\limits_{a,b=\pm }{\chi }_{a,p}^{{\dagger} }{\chi }_{a,p+q}{\psi }_{b,k+q}^{{\dagger} }{\psi }_{b,k}+\frac{4K}{{N}_{z}}\mathop{\sum}\limits_{k,p,q,}\mathop{\sum}\limits_{a,b=\pm }{\chi }_{a,p}^{{\dagger} }{\chi }_{-a,p+q}{\psi }_{b,k+q}^{{\dagger} }{\psi }_{-b,k},$$

(6)

$${V}_{{{{\rm{K-AF}}}}}=-\frac{{{{\rm{i}}}}g}{\sqrt{{N}_{z}}}\mathop{\sum}\limits_{k,q}\mathop{\sum}\limits_{a=\pm }{\phi }_{q}({\chi }_{-a,-k+q}^{{\dagger} }{\psi }_{a,k}^{{\dagger} }+{\chi }_{-a,-k-q}{\psi }_{a,k}),$$

(7)

where ± signs in the subscript indicate two gapless points, ϵ_±,k = vk_x, Δ_±,k = − vk_y, v = 3 Ka, a is the lattice constants, N_z is the number of z-bond. Here we are interested in the symmetric phase of the Kitaev model, so K_x = K_y = K_z ≡ K. Here H_int is four-fermion interactions between itinerant and localized fermions. It turns out that these effective interactions are not relevant in RG sense, and we ignore these terms. Note that they can affect behaviors in weak-coupling high-energy regions, but it is similar to the effects due to the AFM coupling, as discussed in the Discussion section. Therefore we construct the effective model without H_int. Introducing spinors as

$${{{\Psi }}}_{k}={({\psi }_{+,k},{\psi }_{-,-k}^{{\dagger} })}^{T},\,\,\,{X}_{k}={({\chi }_{+,k},{\chi }_{-,-k}^{{\dagger} })}^{T},$$

(8)

one obtains effective Hamiltonian in Dirac form

$$H=\mathop{\sum}\limits_{k}{{{\Psi }}}_{k}^{{\dagger} }(v{k}_{x}{\tau }^{z}+v{k}_{y}{\tau }^{y}){{{\Psi }}}_{k}+2K\mathop{\sum}\limits_{k}{X}_{k}^{{\dagger} }{\tau }^{z}{X}_{k}-\frac{{{{\rm{i}}}}g}{\sqrt{{N}_{z}}}\mathop{\sum}\limits_{k,q}{\phi }_{q}({X}_{k+q}^{{\dagger} }{\tau }^{x}{{{\Psi }}}_{k}-{{{\Psi }}}_{k}^{{\dagger} }{\tau }^{x}{X}_{k-q}).$$

(9)

Including a self-interaction term for AFM fluctuations ϕ, the resulting effective action in the continuum limit is given by

$$\begin{array}{lll}S&=&{S}_{{{{\rm{K}}}}}+{S}_{{{{\rm{AF}}}}}+{S}_{{{{\rm{K-AF}}}}},\\ {S}_{{{{\rm{K}}}}}&=&\int\,\frac{{d}^{3}k}{{(2\pi )}^{3}}\,\left(\bar{{{\Psi }}}(k){{{\rm{i}}}}\gamma \cdot k{{\Psi }}(k)+\bar{X}(k)({{{\rm{i}}}}{\gamma }_{0}{k}_{0}+{{{\rm{i}}}}{{{\boldsymbol{\gamma }}}}\cdot {{{\bf{M}}}})X(k)\right),\\ {S}_{{{{\rm{K-AF}}}}}&=&-{{{\rm{i}}}}g\int\,\frac{{d}^{3}k{d}^{3}q}{{(2\pi )}^{6}}\,\phi (q)\left(\bar{X}(k+q){{\Psi }}(k)-\bar{{{\Psi }}}(k)X(k-q)\right),\\ {S}_{{{{\rm{AF}}}}}&=&\frac{1}{2}\int\,\frac{{d}^{3}k}{{(2\pi )}^{3}}\,\phi (-k)({k}^{2}+r)\phi (k)+\frac{\lambda }{4!}\int\,\frac{{d}^{3}k{d}^{3}p{d}^{3}q}{{(2\pi )}^{9}}\,\phi (-k)\phi (-p-q)\phi (p)\phi (k+q).\end{array}$$

(10)

Here, Ψ(k) and X(k) are Dirac spinors formed by itinerant and localized fermions, respectively, and M = (M, 0), M is the Z₂ flux gap. Interestingly, the Z₂ flux gap appears as a momentum shift of nodal points, and this shift plays a central role in the quantum-critical scaling of dynamic spin susceptibility at the Γ point. There appears an effective ϕ⁴-type field theory of self-interactions³¹, which describes the critical dynamics of the Ising spin fluctuations in the coarse-graining procedure. The details are in Supplementary Notes.

In the following sections, we derive the scaling behavior of the dynamic spin susceptibility and the specific heat based on Eq. (10) in the weak-coupling limit for the high-energy region and also in the strong-coupling limit for the low-energy region.

Weak-coupling high-energy region

In the high-energy region, the coupling becomes weak so we derive the universal scaling function using perturbative analysis. The zigzag AFM order parameter also strongly fluctuates and thus the “localized” X(k) fermions become delocalized due to the interaction S_K-AF. As a result, the two fermionic excitations can be described in the Dirac theory with different Dirac velocities. We first perform the Wilsonian RG analyses of these two itinerant Dirac field models up to the one-loop level and reveal the Wilson–Fisher–Yukawa FP. Then we evaluate the dynamic spin susceptibility at the FP for comparison with the INS results of α-RuCl₃.

Reflecting delocalization of the X_k fermions, we replace γ₀k₀ with γ ⋅ k to modify the S_K term in Eq. (10) as follows;

$${S}_{{{{\rm{K}}}}}\to \int\,\frac{{d}^{3}k}{{(2\pi )}^{3}}\,\left[\bar{{{\Psi }}}(k){{{\rm{i}}}}\gamma \cdot k{{\Psi }}(k)+\bar{X}(k){{{\rm{i}}}}\gamma \cdot (k+M)X(k)\right].$$

(11)

With the modified effective action, we follow the standard Wilsonian RG procedure. We first divide the fields into high- and low-energy components,

$${{\Psi }}(k)={{\Psi }}(k)\theta \left[k({{\Lambda }}/b-k)\right]+{{\Psi }}(k)\theta \left[({{\Lambda }}-k)(k-{{\Lambda }}/b)\right]\equiv {{{\Psi }}}_{l}(k)+{{{\Psi }}}_{h}(k),$$

(12)

and similar to X and ϕ fields. Integrating over high-energy field degree of freedom, i.e., performing the functional integration $\int\,{{{\mathscr{D}}}}{{{\Psi }}}_{h}(k){{{\mathscr{D}}}}{X}_{h}(k){{{\mathscr{D}}}}{\phi }_{h}(k){{{{\rm{e}}}}}^{-S}$ in the perturbative way of the cumulant expansion, we obtain quantum-fluctuation corrections on the dynamics of low-energy degrees of freedom. After rescaling the momentum coordinates and all low-energy fields, we obtain an effective action for the low-energy fields with renormalized couplings. The relations between the low-energy fields and renormalized fields are

$${{{\Psi }}}_{R}(k)={b}^{-2}{Z}_{{{\Psi }}}^{-1/2}{{{\Psi }}}_{l}(k/b),\,\,\,{X}_{R}(k)={b}^{-2}{Z}_{X}^{-1/2}{X}_{l}(k/b),\,\,\,{\psi }_{R}(k)={b}^{-5/2}{Z}_{\phi }^{-1/2}{\psi }_{l}(k/b),$$

(13)

and that between the bare coupling constant and the renormalized ones are

$${g}_{R}={b}^{1/2}{Z}_{g}^{-1}{Z}_{{{\Psi }}}^{1/2}{Z}_{X}^{1/2}{Z}_{\phi }^{1/2}g,\,\,\,{\lambda }_{R}=b{Z}_{\lambda }^{-1}{Z}_{\phi }^{2}\lambda ,\,\,\,{M}_{R}=b{Z}_{M}^{-1}{Z}_{X}M.$$

(14)

Here, the subscript R represents the renormalized field. The first factors, exponents of b in the fields and coupling constants, originate from the classical scaling. The renormalization factors Z_a, a = Ψ, X, ϕ which are defined by ${Z}_{a}^{-1}=1+{\delta }_{a}$ contain quantum corrections δ_a which are calculated from self-energies and vertex corrections.

Within the one-loop level, self-energies and vertex corrections are

$$\begin{array}{lll}{{{\Sigma }}}_{{{\Psi }}}&=&{g}^{2}\int\nolimits_{{{\Lambda }}/b}^{{{\Lambda }}}\frac{{d}^{3}q}{{(2\pi )}^{3}}\,{G}_{X}(k+q){G}_{\phi }(q),\,\,\,{{{\Sigma }}}_{X}={g}^{2}\int\nolimits_{{{\Lambda }}/b}^{{{\Lambda }}}\frac{{d}^{3}q}{{(2\pi )}^{3}}\,{G}_{{{\Psi }}}(k+q){G}_{\phi }(q),\\ {{{\Sigma }}}_{\phi ,1}(q)&=&-2{g}^{2}\int\nolimits_{{{\Lambda }}/b}^{{{\Lambda }}}\frac{{d}^{3}k}{{(2\pi )}^{3}}\,{{{\rm{Tr}}}}\left[{G}_{{{\Psi }}}(k+q){G}_{X}(k)\right],\,\,\,{{{\Sigma }}}_{\phi ,2}(q)=-\frac{\lambda }{2}\int\nolimits_{{{\Lambda }}/b}^{{{\Lambda }}}\frac{{d}^{3}k}{{(2\pi )}^{3}}\,{G}_{\phi }(k),\end{array}$$

(15)

and

$$\begin{array}{lll}{{{\Gamma }}}_{g}&=&-{{{\rm{i}}}}{g}^{3}\int\nolimits_{{{\Lambda }}/b}^{{{\Lambda }}}\frac{{d}^{3}q}{{(2\pi )}^{3}}\,{G}_{\phi }(q){G}_{{{\Psi }}}(q){G}_{X}(q),\\ {{{\Gamma }}}_{\lambda ,1}&=&-\frac{3{\lambda }^{2}}{2}\int\nolimits_{{{\Lambda }}/b}^{{{\Lambda }}}\frac{{d}^{3}q}{{(2\pi )}^{3}}\,{\left[{G}_{\phi }(q)\right]}^{2},\,\,\,{{{\Gamma }}}_{\lambda ,2}={g}^{4}\int\nolimits_{{{\Lambda }}/b}^{{{\Lambda }}}\frac{{d}^{3}q}{{(2\pi )}^{3}}\,{{{\rm{Tr}}}}\left[{G}_{X}(q){G}_{{{\Psi }}}(q){G}_{X}(q){G}_{{{\Psi }}}(q)\right],\end{array}$$

(16)

with Green functions,

$${G}_{{{\Psi }}}(k)=-\frac{{{{\rm{i}}}}\gamma \cdot k}{{k}^{2}},\,\,\,{G}_{X}(k)=-\frac{{{{\rm{i}}}}\gamma \cdot (k+M)}{{(k+M)}^{2}},\,\,\,{G}_{\phi }(k)=\frac{1}{{k}^{2}}.$$

(17)

The diagrams are shown in Fig. 4a. From the self-energies and vertex functions, one can deduce renormalization constants and renormalized couplings. The quantum corrections are δ_a = − ∂_iγ⋅kΣ_a(k)∣_k=0 for Ψ and X fields, and ${\delta }_{a}=-{\partial }_{{k}^{2}}{{{\Sigma }}}_{a}(k){| }_{k = 0}$ for ϕ field from the self-energies, and δ_a = Γ_a from vertex corrections. Then the beta functions for coupling g and λ are given by

$$\begin{array}{lll}{\beta }_{g}&\equiv &\frac{d{g}_{R}}{d\log b}=\frac{{g}_{R}}{2}-\frac{{g}_{R}^{3}}{4{\pi }^{2}}+{{{\mathscr{O}}}}(M),\\ {\beta }_{\lambda }&\equiv &\frac{d{\lambda }_{R}}{d\log b}={\lambda }_{R}-\frac{3{\lambda }_{R}^{2}}{16{\pi }^{2}}+\frac{3{g}_{R}^{4}}{2{\pi }^{2}}+{{{\mathscr{O}}}}(M),\end{array}$$

(18)

and the anomalous scaling dimensions are

$${\eta }_{{{\Psi }}}=\frac{1}{2}\frac{\partial \log {Z}_{{{\Psi }}}}{\partial \log b},\,\,\,{\eta }_{X}=\frac{1}{2}\frac{\partial \log {Z}_{X}}{\partial \log b},\,\,\,{\eta }_{\phi }=\frac{1}{2}\frac{\partial \log {Z}_{\phi }}{\partial \log b}.$$

(19)

See Supplementary Notes for details. The RG flow and the FPs are shown in Fig. 4. As can be seen in the figure, when g = 0, the fermions are decoupled from the zigzag AFM fluctuations, and the system flows towards a well-known stable Wilson–Fisher FP. Turning on the coupling (g ≠ 0) between fermions and zigzag AFM fluctuations, it flows to another FP, Wilson–Fisher–Yukawa FP. Essential information on the interacting FP is the critical exponents to describe anomalous scaling dimensions of the delocalized and itinerant fermion excitations, and the exponents originate from their correlations with the critical Ising spin fluctuations.

Fig. 4: Feynmann diagrams and the renormalization group flow diagram of coupling constants.

a Green functions and one-loop Feynman diagrams for self-energies and vertex functions. b RG flows in a $\tilde{g}$-$\tilde{\lambda }$ coupling space with ${\tilde{g}}^{2}={g}^{2}/8{\pi }^{2}$ and $\tilde{\lambda }=\lambda /8{\pi }^{2}$ by solving the coupled β-functions. Various fixed points (FPs) are indicated, two unstable FPs (black dots) and one stable interacting FP (red dot).

To compare with INS data at Γ point, we calculate uniform spin susceptibility. In order to extract the dynamical spin susceptibility at the Γ-point, we introduce a uniform field Zeeman coupling ${H}_{UZ}=-{g}_{u}{\sum }_{i}{\sigma }_{i}^{z}{H}_{i}^{u}$, which can be reformulated as

$${H}_{UZ}={{{\rm{i}}}}{g}_{u}\int\,\frac{{d}^{3}k{d}^{3}q}{{(2\pi )}^{6}}\,{H}_{u}(q)\left(\bar{X}(k+q){\gamma }_{0}{{\Psi }}(k)-\bar{{{\Psi }}}(k){\gamma }_{0}X(k-q)\right).$$

(20)

Here, we do not take into account the coupling between the zigzag AFM ϕ(k) and the uniform field since its effect is negligible in comparison with the ferro-component contribution of the Γ-point. Then, the spin susceptibility is given by

$${\chi }_{u}=\frac{1}{V}\frac{{\delta }^{2}\log {Z}_{{{{\rm{eff}}}}}[H(q)]}{\delta {H}_{u}(-q)\delta {H}_{u}(q)}{\left\vert \right.}_{H(q) = 0}=-{g}_{u}^{2}{Z}_{{{\Psi }}}{Z}_{X}\int\,\frac{{d}^{3}k}{{(2\pi )}^{3}}\,{{{\rm{Tr}}}}\left\{\left[{G}_{X}(k+q)+{G}_{X}(k-q)\right]{\gamma }_{0}{G}_{{{\Psi }}}(k){\gamma }_{0}\right\},$$

(21)

where Z_eff is the effective partition function, including the Zeeman term. The renormalization factors play roles of anomalous scaling dimensions in the spin susceptibility and account for the absence of well-defined quasiparticle excitations near the interacting fixed point.

After the integration and taking into account the field renormalization factors and anomalous dimensions, one can find the scaling theory for the spin susceptibility,

$${{{\rm{Im}}}}{\chi }_{u}(\omega ,M,T)={b}^{1+2{\eta }_{{{\Psi }}}+2{\eta }_{X}}{{{\rm{Im}}}}{\chi }_{u}\left(\frac{\omega }{b},\frac{M}{{b}^{{y}_{M}}},\frac{T}{b}\right)={T}^{1+2{\eta }_{{{\Psi }}}+2{\eta }_{X}}{{{\rm{Im}}}}{\chi }_{u}\left(\frac{\omega }{T},\frac{M}{{T}^{{y}_{M}}},1\right),$$

(22)

where we set b = T in the second equality and y_M is the scaling dimension of M which is calculated from ${M}_{R}=b{Z}_{M}^{-1}{Z}_{X}M\approx {b}^{{y}_{M}}M$. Assuming $M/{T}^{{y}_{M}}\ll 1$, one can expand ${\chi }_{u}(\omega /T,M/{T}^{{y}_{M}},1)$ in $M/{T}^{{y}_{M}}$. The lowest non-vanishing term is ${(M/{T}^{{y}_{M}})}^{2}$ and in the quantum-critical regime of ω/T ≳ 1, the spin susceptibility is given by

$${{{\rm{Im}}}}{\chi }_{u}(\omega ,M,T)={\chi }_{0}{M}^{2}{T}^{-2{y}_{M}+1+2{\eta }_{{{\Psi }}}+2{\eta }_{X}}{\left(\frac{T}{\omega }\right)}^{1-2{\eta }_{{{\Psi }}}-2{\eta }_{X}}\tanh \frac{\omega }{4T},$$

(23)

where χ₀ is a cutoff dependent and non-universal constant. Within the one-loop level, we obtained the anomalous scaling dimension of the spin susceptibility η_χ = 2y_M − (1 + 2η_Ψ + 2η_X) = 1 and critical exponent 1 − 2η_Ψ − 2η_X ≈ 1.25. Then the universal scaling function is

$${T}^{\alpha }\,{{{{\rm{Im}}}}\chi (\omega ,T)}_{Q = {{\Gamma }}}={\chi }_{0}{M}^{2}{\left(\frac{T}{\omega }\right)}^{1.25}\tanh \frac{\omega }{4T}.$$

(24)

with α = 1. Here, $\tanh \frac{\omega }{4T}$ reflects “particle”–“hole” excitations of both fractionalized fermions. M is the momentum-space distance between the Dirac points of the Majorana fermion and the Z₂ flux and reduces to the Z₂ flux gap at zero temperature. It is remarkable to observe that the spin susceptibility at the Γ-point is proportional to M². Although the spectral intensity of the two-particle correlation function should vanish at the Γ-point with M = 0, the appearance of the spectral intensity at the Γ-point indicates that a shift in the nodal point effectively retains the Z₂ flux gap, like the inter-band transition gap.

To investigate the critical behavior of α-RuCl₃, the neutron scattering results at Q = Γ with diverse temperatures are compared to the scaling function model. Here, the imaginary part of the dynamic spin susceptibility is extracted through the fluctuation-dissipation theorem³³${{{\rm{Im}}}}\chi \left({{{\bf{Q}}}},\omega \right)\equiv {\chi }^{{\prime\prime} }\left({{{\bf{Q}}}},\omega \right)=S({{{\bf{Q}}}},\omega )\left(1-{e}^{-\hslash \omega /{k}_{{{{\rm{B}}}}}T}\right)$ from S(Q, ω) measured at T = 2.3 K, 6 K, 25 K, 75 K, and 150 K in a full energy range of 1meV < ℏω < 15meV available in the present experimental conditions (see Sec. A in SI). Figure 5 displays χ^″(Γ, ω)T^α versus ℏω/k_BT in the log–log plot. The scaling function data extracted from the zero-field INS S(Γ, ω) in the ranges ℏω = [1, 9] meV with incident neutron energy E_i = 22 meV and ℏω = [6, 15] meV with E_i = 50 meV at T = 2.3 K, 6 K, 25 K, 75 K, and 100 K. The data are compared with the theoretical universal scaling function (blue solid line) for the weak-coupling quantum criticality, Eq. (24). The fitting value of the exponent α is 0.91, which is close to the theoretical value 1. The χ^″(Γ, ω)T^α value itself strongly varies with energy and temperature, while those values collapse onto a single line over two decades for ℏω ≳ 5 meV. Such behaviors certainly reflect the universal scaling involving the weak-coupling quantum criticality applicable to the high-energy scale. This merging line corresponds to the universal law for χ^″(Γ, ω)T^α derived from the theoretical model calculations as described above. Meanwhile, one can recognize that the dynamic spin susceptibility does not follow the university scaling at low energies, and the deviation becomes considerable for ℏω ≲ 4 meV commonly at different temperatures as can be seen in Fig. 5 (blurred circle plots). This common deviation at the low energies indicates that the weak-coupling quantum criticality is valid only at the high energies (also see Supplementary Fig. 1).

Fig. 5: Scaling plot in ℏω/k_BT for the dynamic spin susceptibility at high energies, ℏω ≥4 meV.

Blurred circles present the data in the low-energy range ℏω = [1, 4] meV, which are out of the universal scaling behavior. Error bars represent 1 standard deviation.

Strong-coupling low-energy region

In the low-energy region, the perturbative analysis is not applicable since the strong-coupling physics emerges. Thus we first examine the INS results for a possibility of a universal scaling at the low energies and construct an empirical formula for the dynamic susceptibility in the effective model Hamiltonian with the local quantum criticality. Then we check the validity of the criticality using self-consistent analyses based on the DMFT description.

To examine the low-energy universal scaling of the dynamic spin susceptibility, we measure S(Q, ω) at more diverse temperatures of T = 2 K, 10 K, 16 K, 25 K, 40 K, 75 K, 100 K, 125 K, and 160 K in a low-energy range of 1 meV≤ℏω≤5 meV and extract χ^″(Γ, ω)T^0.14 values scaled in ℏω/k_BT, as shown in Fig. 6. Remarkably, the χ^″(Γ, ω)T^0.14 values also merge to a single line of another universal scaling distinguished from the high-energy one. The universal scaling behavior drastically changes in the low-energy scale below ~ 5meV. The slop changes its sign across ℏω/k_BT ~ 2. In addition, the low-energy spectral weight is rather uniformly distributed in the momentum space around Q = Γ, differently from the high-energy spectral weight (referred to Fig. 5). These two aspects recall an effective Bose–Fermi Kondo-type model adopted to the heavy-fermion local quantum criticality in a system with magnetic impurity states, collective bosonic modes, and dispersive fermions³⁴. Those are analogous to the localized Z₂ fluxes, Ising AFM fluctuations, and itinerant Majorana fermions appearing in α-RuCl₃, respectively. This local quantum criticality is schematically pictured in Fig. 3c. Here, the AFM fluctuation interacts with the Z₂ fluxes and MFs to become locally critical.

Fig. 6: Scaling plot for the dynamic spin susceptibility obtained at low energies, ℏω ≤5 meV.

The quantity χ^″T^α with α = 0.14 is plotted against ℏω/k_BT. The red line is a fit to the local quantum criticality model as described in the text. The gray circles presenting the 2 K data deviate from the universal scaling due to the dominant magnon excitation at a low-energy AFM state below T_N ≈ 6.5 K. Error bars represent 1 standard deviation.

The previous study for the heavy-fermion local quantum criticality³ suggests a scaling expression for the dynamic spin susceptibility

$$\chi \left(\omega ,T,H\right)=\frac{A}{{\left(aT-{{{\rm{i}}}}\omega \right)}^{\alpha }+{a}^{\alpha }{T}^{* \alpha }},$$

(25)

which represents the susceptibility of a local moment coupled to a critical continuum. Here, a, A, and α are parameters, T^* is the characteristic temperature, shown in Fig. 1a. A key feature of this local spin susceptibility is the branch-cut singularity with a critical exponent α and the existence of the huge dissipation proportional to the transfer energy. We derive the universal scaling function at Γ for the strong-coupling local quantum criticality in a limit of the inverse of quantum coherence time T^* → 0 (QCP) as follows (see Supplementary Notes for details);

$${T}^{\alpha }\,{{{{\rm{Im}}}}\chi (\omega ,T)}_{{{{\bf{Q}}}} = {{\Gamma }}}=\frac{A}{{\left({a}^{2}{T}^{2}+{\omega }^{2}\right)}^{\alpha /2}}\sin \left\{\alpha \,{\tan }^{-1}\left(\frac{\omega }{aT}\right)\right\}.$$

(26)

As can be seen in Fig. 6, this theoretical scaling function well explains the low-energy universal scaling behavior obtained from the INS results ranging over about two orders of magnitude in ℏω/k_BT above T_N with α ≈ 0.14, the overall constant A ≈ 63.9, and the order 1 constant a ≈ 0.88.

One may point out that the high-temperature INS data even above 100 K but below 5 meV follow the strong-coupling locally quantum-critical scaling behavior, although those data points are in ℏω/k_BT < 1, which may not belong to the quantum-critical scaling region. Since the temperature would play the role of a lower cutoff in the RG flow of the spin-spin correlation function, it is natural to expect that the potential existence of other length scales at low energies might spoil the scaling behavior in ℏω/k_BT < 1. Interestingly, the present scaling analysis shows the existence of this high-temperature but low-energy scaling behavior, although its origin is not clear.

To confirm the existence of the local quantum criticality at low temperatures in the vicinity of the genuine QCP, we perform a DMFT analysis for the localized Z₂ flux excitations, itinerant MFs, and locally critical Ising AFM spin fluctuations within a non-crossing approximation^34,35. Compared to the Gross–Neveu–Yukawa-type model for the weak-coupling quantum criticality at high temperatures, two essential modifications have been made; the velocity of Z₂ flux fluctuations is strongly renormalized to vanish, and the dynamics of Ising spin excitations is governed by the inverse of the locally critical spin susceptibility instead of their relativistic dispersion.

Based on the empirical form of the spin susceptibility, Eq. (25), we write an effective action for the low-energy region as S = S_K + S_AF + S_K-AF. This action is the same as Eq. (10) (in Matsubara frequency space³⁶) except for S_AF which is modified as follows,

$$\begin{array}{lll}{S}_{{{{\rm{AF}}}}}=\frac{1}{2}\int\nolimits_{0}^{\beta }\,d\tau d{\tau }^{{\prime} }\int\,{d}^{2}x\,\phi (\tau ,x){\chi }_{{{{\rm{LQCP}}}}}^{-1}(\tau -{\tau }^{{\prime} })\phi ({\tau }^{{\prime} },x),\\ {\chi }_{{{{\rm{LQCP}}}}}^{-1}({{{\rm{i}}}}\omega ,T,H)=\left[{(aT+| \omega | )}^{\alpha }+{a}^{\alpha }{T}^{* \alpha }\right]/A.\end{array}$$

(27)

Note that ${\chi }_{{{{\rm{LQCP}}}}}^{-1}$ is the inverse of Eq. (25). This expression looks quite similar to that of the description of high-energy delocalized quantum criticality. However, there exists an essential difference in that both the spin and Z₂ flux dynamics are local. We perform the DMFT analysis in the non-crossing approximation^37,38, which confirms that this renormalization ansatz is self-consistent.

The one-loop self-energies for Ψ and X fermions are

$$\begin{array}{lll}{{{\Sigma }}}_{{{\Psi }}}({{{\rm{i}}}}\omega ,{{{\bf{k}}}})=-\frac{{g}^{2}}{2}{\int}_{{{{\rm{i}}}}{{\Omega }},{{{\bf{q}}}}}{\chi }_{{{{\rm{LQCP}}}}}({{{\rm{i}}}}{{\Omega }}){{{{\mathscr{G}}}}}_{X}({{{\rm{i}}}}\omega -{{{\rm{i}}}}{{\Omega }},{{{\bf{k}}}}-{{{\bf{q}}}}),\\ {{{\Sigma }}}_{X}({{{\rm{i}}}}\omega ,{{{\bf{k}}}})=-\frac{{g}^{2}}{2}{\int}_{{{{\rm{i}}}}{{\Omega }},{{{\bf{q}}}}}{\chi }_{{{{\rm{LQCP}}}}}({{{\rm{i}}}}{{\Omega }}){{{{\mathscr{G}}}}}_{{{\Psi }}}({{{\rm{i}}}}\omega -{{{\rm{i}}}}{{\Omega }},{{{\bf{k}}}}-{{{\bf{q}}}}),\end{array}$$

(28)

where ${\int}_{{{{\rm{i}}}}{{\Omega }},{{{\bf{q}}}}}\equiv \frac{1}{\beta }{\sum }_{{{{\rm{i}}}}{{\Omega }}}\int\,\frac{{d}^{2}q}{{(2\pi )}^{2}}$ and ${{{{\mathscr{G}}}}}_{{{\Psi }},X}$ are renormalized Green’s functions given by the Dyson equations

$$\begin{array}{lll}{{{{\mathscr{G}}}}}_{{{\Psi }}}^{-1}({{{\rm{i}}}}\omega ,{{{\bf{k}}}})={{{\rm{i}}}}\omega {\gamma }^{\tau }+{{{\rm{i}}}}{{{\bf{k}}}}\cdot {{{\boldsymbol{\gamma }}}}-{{{\Sigma }}}_{{{\Psi }}}({{{\rm{i}}}}\omega ,{{{\bf{k}}}}),\\ {{{{\mathscr{G}}}}}_{X}^{-1}({{{\rm{i}}}}\omega ,{{{\bf{k}}}})={{{\rm{i}}}}\omega {\gamma }^{\tau }+{{{\rm{i}}}}{{{\bf{M}}}}\cdot {{{\boldsymbol{\gamma }}}}-{{{\Sigma }}}_{X}({{{\rm{i}}}}\omega ,{{{\bf{k}}}}).\end{array}$$

(29)

Here, γ^a, a = τ, 1, 2 are the Euclidean forms of Dirac gamma matrices in two-dimension. The self-consistent condition is formed from the renormalized spin susceptibility given by

$${\chi }_{{{{\rm{LQCP}}}}}({{{\rm{i}}}}{{\Omega }})={\int}_{{{{\rm{i}}}}\omega ,{{{\bf{k}}}}}{{{\rm{Tr}}}}\left[{{{{\mathscr{G}}}}}_{X}({{{\rm{i}}}}\omega ,{{{\bf{k}}}}){{{{\mathscr{G}}}}}_{{{\Psi }}}({{{\rm{i}}}}\omega +{{{\rm{i}}}}{{\Omega }},{{{\bf{k}}}}+{{{\bf{q}}}})\right],$$

(30)

Resorting to self-consistent analyses in the non-crossing approximation, we found the susceptibility constraint for the power-law behavior with the critical exponent α as ${\chi }^{-1}(\omega ,T)\propto {\left(aT-{{{\rm{i}}}}\omega \right)}^{\alpha }$, although a reliable α-value is hard to be determined theoretically within the present mean-field analysis for the strong-coupling limit. Introduction of higher-order perturbative corrections would yield the exponent α to be positive due to unitarity, consistent with the phenomenological value ≈ 0.14 determined from the INS results. These DMFT analyses at least validate the existence of the heavy-fermion-like local quantum criticality at low temperatures due to emergent local dynamics of the Z₂ flux and Ising AFM fluctuations.

To further confirm the local quantum criticality in α-RuCl₃, we also performed ac-magnetic susceptibility measurement in a nonzero applied magnetic field. Figure 7a shows the real part of the ac magnetic susceptibility ${\chi }_{{{{\rm{ac}}}}}^{{\prime} }(T,H)$ measured with magnetic fields along H//a (see the inset of Fig. 7b for the field direction), representing the phase diagram in the temperature and the magnetic field. The low-temperature ${\chi }_{{{{\rm{ac}}}}}^{{\prime} }(H)$ below 4 K reveals two anomaly peaks, indicating phase transitions between zigzag AFM1 (ZZ1), zigzag AFM2 (ZZ2), and polarized FM (PF), in turn. The appearance of the multi phases in the magnetic field is consistent with the phase diagrams provided by previously reported specific heat, ac-magnetic susceptibility, and neutron diffraction measurements^39,40. Figure 7b shows ${\chi }_{{{{\rm{ac}}}}}^{{\prime} }(T)$ at various magnetic fields near the phase boundary between the ZZ2 and PF. In particular, ${\chi }_{{{{\rm{ac}}}}}^{{\prime} }(T)$ exhibits a power-law behavior below 14 K at H_C = 7.2 T, revealing a criticality where the zigzag antiferromagnetic order is suppressed by the magnetic field. The collected ${\chi }_{{{{\rm{ac}}}}}^{{\prime} }(T)$ are scaled with ${\chi }_{{{{\rm{ac}}}}}^{{\prime} }{T}^{\alpha }$ with α = 0.14, and this quantity collapses onto a single line as a function of (H − H_C)/k_BT for the fields above H_C. The observed critical exponent α = 0.14 is consistent with the critical exponent from the dynamical spin susceptibility at the low energy, re-confirming the local quantum criticality in the α-RuCl₃.

Fig. 7: ac-magnetic susceptibility at nonzero applied magnetic field.

a Temperature-magnetic field contour plot of the real part of the ac-magnetic susceptibility ${\chi }_{{{{\rm{ac}}}}}^{{\prime} }(T,H)$ for applied magnetic field along a axis of the honeycomb lattice, as depicted in the inset of (b). The black circles indicate the phase boundaries between zigzag AFM1 (ZZ1), zigzag AFM2 (ZZ2), and polarized ferromagnet (PF). b ${\chi }_{{{{\rm{ac}}}}}^{{\prime} }(T)$ measured at various fields near the phase boundary between the ZZ2 and PF, displayed in log–log plot. ${\chi }_{{{{\rm{ac}}}}}^{{\prime} }$ measured at H_C = 7.2 T shows power-law behavior, representing the criticality, and this field value is indicated with the blue arrow in (a). The black solid line is a linear guide to the eyes. c A scaled plot of the ac-magnetic susceptibility, plotted as ${\chi }_{{{{\rm{ac}}}}}^{{\prime} }{T}^{\alpha }$ with α = 0.14 as a function of μ_B(H − H_C)/k_BT.

Magnetic-specific heat: Weak to Strong-coupling crossover

The crossover behavior of the quantum criticality is also observable in the magnetic-specific heat C_m of α-RuCl₃²⁰. As shown in Fig. 8a, C_m exhibits a low-temperature plateau up to ~50 K above T_N and then follows a T-linear like behavior up to T_H ~100 K. The latter, which was attributed to the Dirac-like itinerant MFs²⁹, indeed agrees well with the contribution calculated in a system with free Dirac fermions, consistent with the weak-coupling quantum criticality. Remarkably, the plateau feature, which has been puzzling, turns out to be understood with the low-energy local quantum criticality. Using the dynamic spin susceptibility, we construct a standard form of the free energy $F\left(T,H\right)=-T{\sum }_{{{{\rm{i}}}}\omega }\log \chi ({{{\rm{i}}}}\omega ,T,H)$ and calculate ${C}_{{{{\rm{m}}}}}\left(T,H=0\right)=-T{\partial }^{2}F/\partial {T}^{2}$ with the fitting parameters α ≈ 0.14 and a ≈ 0.88 obtained from the low-energy scale INS results (see Supplementary Notes and Supplementary Fig. 10 for details). As can be seen in the figure, the calculated C_m reasonably well reproduces the plateau feature above T_N. This result implies that most of the entropy is given by the critically fluctuating local moments in this regime.

Fig. 8: Scaling behavior of the magnetic-specific heat of α-RuCl₃.

a Magnetic-specific heat (magnetic contribution) C_m obtained at the zero magnetic field and theoretical model calculations. b Log–log plot of the Néel temperature T_N under magnetic fields H as a function of δh = 1 − H/H_C (H//a) with the critical field H_c ≈ 6T. The blue-filled circles denote T_N(H) extracted from the AFM peak position in C_m(H, T). The red dashed line is given by scaling function for T_N ∝ δh^νz, where ν is the critical exponent of the correlation length and z is the dynamical critical exponent. A universal scaling behavior of C_m is presented in the inset, where the scaling function data $\left(\frac{{C}_{{{{\rm{m}}}}}}{T}\right){\delta h}^{\nu z}$ for different H-fields merge into a single universal curve above T_N(H) with νz ≈ 0.125 in the log–log plot as a function of T/T_N(H).

Besides the plateau feature, the strong-coupling local quantum criticality also predicts a scaling behavior of the specific heat C_m (also see Supplementary Notes). Now the energy scale separated from QCP corresponds to T_N(H) = ${T}_{{{{\rm{N}}}}}(0){\left(1-H/{H}_{{{{\rm{C}}}}}\right)}^{\nu z}$, inverse of the quantum coherence time at an H-field. The critical exponent νz involves the critical exponent ν of the correlation length and the dynamic critical exponent z. In the local quantum criticality, ν → 0 (local) and z → ∞ yield a finite νz. To determine the exponent νz, we measured the specific heat C_m at various magnetic fields below the critical field H_C ≈ 6T, where T_N(H_C) is supposed to become zero. Figure 8b shows T_N vs. δh = 1 − H/H_C and the best fit is obtained with νz ≈ 0.125. Using this value, we examine the scaling behavior of $\left({C}_{{{{\rm{m}}}}}/T\right){\delta h}^{\nu z}$ as a function of T/T_N(H). As can be seen in the inset, all $\left({C}_{{{{\rm{m}}}}}/T\right){\delta h}^{\nu z}$ at different H-fields merge into a universal scaling curve, indicating that the effective spatial dimension, in which critical fluctuations dominate the entropy-carrying, is extremely local. This result confirms that the low-temperature specific heat above T_N is governed by the strong-coupling local quantum criticality.

Discussion

In this study, have shown the crossover behavior of α-RuCl₃ from the high-energy weak-coupling critical region to the low-energy strong-coupling critical region above T_N as described in Fig. 1. We identified a Wilson–Fisher–Yukawa FP which governs the universal physics in the high-energy region. It is essentially the same physics as that of the pure Kitaev model. Although the zigzag Ising AFM fluctuations are introduced in the present effective field-theory description, they just contribute short-ranged effective interactions to both matter fluctuations, itinerant MFs and localized Z₂-flux excitations, in the high-temperature quantum-critical regime. In this respect, it is not surprising to have a reasonable agreement between the experiment and the pure Kitaev theory, and the essential ingredients in our field-theory description are almost the same as those of the simulation from the pure Kitaev model^19,20,29,30. Here, we want to emphasize that the present study on the Kitaev-AFM model determines the explicit formula for the scaling function, Eq. (24), which cannot be obtained from previous numerical studies.

The more interesting discovery lies in the low-energy, strong-coupling region. We demonstrated experimentally and theoretically that the spin dynamics follow the heavy-fermion-type strong-coupling physics at low energies. We could show that this emergent strong-coupling local quantum criticality at low energies appears from the weakly coupled rather conventional quantum criticality at high energies. This weak-coupling (Wilson–Fisher type) to strong-coupling (locally critical heavy-fermion type) quantum criticality crossover revealed in α-RuCl₃ has not been expected before. The local quantum criticality is cross-checked both theoretically and experimentally; self-consistent analysis based on the DMFT description and the magnetic-specific heat measurement, respectively. The scaling behavior at low temperatures above T_N indicates that the critical fluctuations dominating the entropy-carrying are extremely local. Unfortunately, we could not explicitly derive the crossover regime since it requires a non-perturbative theoretical approach, which is quite complicated and too difficult. Instead, we verified the existence of the heavy-fermion-like strong-coupling FP in a self-consistent way based on the DMFT. Again, we point out that this strong-coupling phenomenon has never been either observed or discussed in the research of α-RuCl₃.

In α-RuCl₃, it is well known that the symmetric Γ-term is as large as the Kitaev term, and there have been many studies on the effect on the Kitaev spin liquid phase^{41,42,43,44,45,46,47}. Our model contains the Kitaev term coupled with Ising fluctuations but lacks the Γ-term. However, the antiferromagnetic zigzag order and the corresponding Ising spin excitation result from possible interplays among the Γ-term, the Kitaev interaction term, and the Heisenberg exchange term in the microscopic lattice model perspectives. In this respect, the role of the Γ-term in the ground state and its collective excitation has been taken into account rather “effectively.” On the other hand, there can be additional interactions between Ising spin fluctuations in the effective field theory induced by the Γ-term. Recalling that four-fermion local interaction in the two-dimensional Dirac theory, possibly allowed by the Γ-term, are RG irrelevant for quantum criticality, we speculate that the Γ-term does not affect much the critical behavior of Ising spin fluctuations. The Γ-term has a form

$${H}_{{{\Gamma }}}={{{\Gamma }}}_{x}\mathop{\sum}\limits_{x{{{\rm{-bonds}}}}}({S}_{j}^{y}{S}_{k}^{z}+{S}_{j}^{z}{S}_{k}^{y})+{{{\Gamma }}}_{y}\mathop{\sum}\limits_{y{{{\rm{-bond}}}}}({S}_{j}^{z}{S}_{k}^{x}+{S}_{j}^{x}{S}_{k}^{z})+{{{\Gamma }}}_{z}\mathop{\sum}\limits_{z{{{\rm{-bond}}}}}({S}_{j}^{x}{S}_{k}^{y}+{S}_{j}^{y}{S}_{k}^{x}),$$

(31)

which couples the spin z-component (Ising) to the x-, y-component. Thus, the Γ-term shows the spin exchange coupling between the gapless critical degrees of freedom (Ising spin excitations along the z-direction) and the gapped spin excitations of the x-, y-direction. In this respect, it is natural to expect that the Γ-term is irrelevant to the Ising quantum criticality. In addition, for the high-energy weak-coupling region, the previous experiment²⁰ shows that the pure Kitaev model without the Γ-term well explains the behavior above the temperature 50 K. Therefore, as far as quantum criticality is concerned, the Γ-term does not affect physics much. For anisotropy in the Γ-term, i.e., different coupling strengths for different bonds, it is usually irrelevant to the criticality due to the symmetry of Dirac fermions.

Previously, we pointed out that the high-energy quantum-critical scaling behavior can be explained by two kinds of emergent Majorana fermions⁴⁸. In particular, the Z₂ flux excitations are coupled with the itinerant fermions, and these effective interactions are responsible for the weak-coupling high-energy quantum-critical scaling behavior in the high-frequency INS data. The relevance of these many-body interactions in the spin-spin correlation function has also been discussed for the pure Kitaev model⁴⁹. Actually, we confirmed similar high-energy quantum-critical scaling behavior in the quantum Monte Carlo simulation for the pure Kitaev model^19,20,29,30.

It is an essential question whether or not the pure Kitaev physics gives rise to the strong-coupling low-energy quantum-critical scaling behavior in the low-frequency INS data. Since the Z₂ flux excitations coupled with the itinerant fermions are localized at low energies, one may expect strong-coupling behavior in that energy scale. Here we emphasize that role of the quantum-critical Ising-type AFM fluctuations is essential in the appearance of the local quantum criticality. The existence of such quantum-critical spin fluctuations results in long-range singular interactions between the Z₂ flux and itinerant fermion excitations along the time direction. However, the strong-coupling quantum criticality is not possible in the pure Kitaev model since the effective many-body interactions are short-ranged and non-singular to become irrelevant at low energies due to the formation of the Z₂ flux gap. Indeed, we confirmed that the low-frequency INS data significantly deviates from the simulation results for the pure Kitaev model at low energies²⁰.

Note that the existence itself of two FPs is not surprising. For example, suppose a scalar field theory with an effective ϕ⁴-type interaction, regarded to be an effective field theory for a transverse-field Ising lattice model⁵⁰. This field theory is well known to show its RG flow from a non-interacting Gaussian FP at the high-energy UV regime to an interacting Wilson–Fisher one at the low-energy IR regime⁵¹. In quantum chromodynamics, there is an RG flow from an (“almost” non-interacting) asymptotically free theory to a strong-coupling confinement phase⁵¹. Here, we have an RG flow between the weak-coupling Wilson–Fisher-type “conventional” UV FP and the strong-coupling heavy-fermion-type unconventional or local IR FP. A remarkable point is that we reveal the nature of the IR FP in this Kitaev-type material α-RuCl₃. In particular, this IR FP is strongly correlated to be locally quantum critical. The emergence of this heavy-fermion-type strong-coupling FP in this material is completely unexpected.

One may criticize that the heavy-fermion system shows a similar weak-coupling to strong-coupling quantum criticality crossover near the heavy-fermion magnetic QCP. Indeed, some crossover behaviors have been observed in thermodynamics and transport measurements⁵². However, these crossover behaviors were not clearly understood both experimentally and theoretically. For example, there is a crossover behavior in the specific heat of YbRh₂Si₂ near a magnetic field-tuned QCP⁵². One may claim that the high-temperature region would be governed by the Hertz–Moriya-Millis theory, a standard weak-coupling theory for heavy-fermion quantum criticality⁵³. Meanwhile, there is no consensus for the low-temperature anomalous behavior, not understood as far as we know. In addition, there is a classical paper on INS measurements for CeCu_(6-x)Au_x³⁴, in which the low-energy spin dynamics was described in a momentum-independent local form with ω/T scaling. The origin of this functional form was proposed based on a DMFT framework, but the high-energy spin dynamics were not clarified in the study, and it has not yet been understood how the spin dynamics evolve from UV to IR.

Analogous to the crossover between the weak-coupling Hertz–Moriya–Millis quantum criticality and the strong-coupling local quantum criticality in heavy-fermion systems, we verified a similar quantum criticality crossover behavior in α-RuCl₃ not only theoretically but also experimentally. Our study verifies the quantum criticality crossover behavior in α-RuCl₃. A similar crossover was suggested in the heavy-fermion system, but its mechanism has not been understood in our opinion.

If one could simulate the Kitaev–Heisenberg lattice model¹⁸ and calculate the spin-spin correlation function in a brute force way, we believe that the low-energy strong-coupling quantum-critical physics can be verified theoretically. It remains as an interesting future research. In this respect, an interesting message given by the present study is that the Kitaev–Heisenberg lattice model (with a gamma term) would show the weak-coupling to strong-coupling quantum criticality crossover behavior from UV to IR. To confirm the locally quantum-critical scaling function at low energies more transparently, we have to show momentum independence of the low-energy spin spectrum. In other words, we have to investigate the scaling plot at other transfer momentum points in our neutron scattering measurements. In addition, we can calculate both longitudinal and transverse thermal conductivities based on this locally quantum-critical scaling function for the spin spectrum. Resorting to the DMFT framework with this local spin spectrum, we calculate the self-energy of the itinerant fractionalized fermion excitations, which gives the temperature dependence of their scattering rate. Here, the main point is that localization of Z₂ gauge fluxes causes that of Ising antiferromagnetic fluctuations, both of which are coupled to the delocalized fractional excitations. As a result, we suspect that both thermal transport coefficients would show effectively a metal (UV) to insulator (IR) crossover behavior due to the localization physics. We expect that this physics may be reflected in a H/T scaling function for the thermal conductivities.

We believe that our discovery of the crossover behavior from deconfined weak-coupling “non-local” quantum criticality to deconfined strong-coupling “local” quantum criticality in α-RuCl₃ opens an intriguing research field of critical quantum spin liquids, which results from the interplay between the spontaneous symmetry breaking and the topological ordering. In particular, thermal transport properties in α-RuCl₃ would reveal transport phenomena distinguishable from existing ones, giving rise to a unique universal scaling law of the transport properties due to the fade-out of well-defined fractionalized excitations in spite of the topological ordering. In this aspect, α-RuCl₃ provides an ideal platform to explore a unique universality class, where the universal scaling laws govern the thermodynamic, spectroscopic, and transport properties.

Methods

Experimental details

Single crystalline α-RuCl₃ samples were prepared using the vacuum sublimation method as described in ref. ²⁰. The crystal orientation was determined by using the X-ray Laue. The ac-magnetic susceptibility and specific heat of α-RuCl₃ were measured by using the conventional AC Measurement System II (ACMS II) and calorimeter equipped at a commercial Quantum Design Physical Property Measurement System (PPMS-Dynacool), respectively. The ac-magnetic susceptibility was measured at 500 Hz with an oscillating field of 10 Oe.

The zero-field INS measurements were performed by using MERLIN and LET time-of-flight spectrometers at the ISIS spallation neutron source in Rutherford Appleton Laboratory, UK. 165 pieces of α-RuCl₃ single crystals with the total mass ~5.5 g were co-aligned on an aluminum plate with the (0, K, L) scattering plane. The samples were placed under a liquid helium flow-type cryostat with a temperature control ranging from 2 to 290 K. In the MELRIN experiments, we used a chopper frequency of 300 Hz, which provides E_i = 12 meV, 22 meV, and 50 meV of incident neutron energies with FWHM (full width at the half maximum) energy resolutions of 0.34 meV, 0.75 meV, and 2.23 meV at elastic scattering, respectively. The measurements were performed for the sample rotation from − 52° to 52° with 4° step referring to 0° at k_i//c^*. The LET experiments were performed at E_i = 10 meV with the energy resolution of 0.36 meV (FWHM) for the elastic scattering, and the sample rotation from − 30° to 30° with 5° step relative to k_i//c^*. The background signals were separately obtained by using an identical aluminum sample holder both in the MERLIN and LET experiments for the background correction. INS data were normalized and converted to the unit for the neutron scattering function by using the incoherent neutron scattering intensity of a standard reference vanadium sample.

The data presented in Figs. 5 and 6 were obtained by integration over [0, 0, L] = [ − 2.5, 2.5], [0, K, 0] = [ − 0.17, 0.17], and [H, − 0.5H, 0] = [ − 0.17, 0.17]. The magnetic form factor contribution from the L-component in the integrated data was corrected by dividing with the Ru³⁺ magnetic form factor at each data point²⁰, and the scaled data were compared with the theoretical model calculations for S(Γ, ω). All the data were analyzed by using HORACE software distributed by ISIS⁵⁴.