A quantum annealer with fully programmable all-to-all coupling via Floquet engineering

Abstract

Quantum annealing is a promising approach to heuristically solving difficult combinatorial optimization problems. However, the connectivity limitations in current devices lead to an exponential degradation of performance on general problems. We propose an architecture for a quantum annealer that achieves full connectivity and full programmability while using a number of physical resources only linear in the number of spins. We do so by application of carefully engineered periodic modulations of oscillator-based qubits, resulting in a Floquet Hamiltonian in which all the interactions are tunable. This flexibility comes at the cost of the coupling strengths between qubits being smaller than they would be compared with direct coupling, which increases the demand on coherence times with increasing problem size. We analyze a specific hardware proposal of our architecture based on Josephson parametric oscillators. Our results show how the minimum-coherence-time requirements imposed by our scheme scale, and we find that the requirements are not prohibitive for fully connected problems with up to at least 1000 spins. Our approach could also have impact beyond quantum annealing, since it readily extends to bosonic quantum simulators, and would allow the study of models with arbitrary connectivity between lattice sites.

Introduction

Quantum annealers are computational devices designed for solving combinatorial optimization problems, most typically Ising optimization problems^1,2,3. An Ising problem is specified by connections among N spins on a graph, as well as local fields on each spin. One of the foremost challenges in the experimental realization of quantum annealers is the requirement that quantum annealers be able to represent densely connected Ising problems with minimal overhead in the number of qubits (and other physical components) used^4,5,6,7. If a quantum annealer is not able to directly represent a particular problem because the problem graph has higher connectivity than the physical annealer does, then one incurs a penalty in the number of qubits needed to represent the Ising problem. For example, the largest fully connected Ising problem that can be represented in the D-Wave 2000-qubit quantum annealer is one that has N = 64 spins⁶; this limitation arises because the connectivity in this particular quantum annealer is very sparse (the connectivity graph has maximum degree six).

Superconducting circuits are one of the most prominent technologies for realizing quantum information processing devices, including quantum annealers, and they form the basis for many of the major projects to construct experimental quantum annealers^8,9,10. However, when qubit connectivity is achieved via physical pairwise couplers (as is the case for the efforts described in refs. ^8,9,10), there is a substantial engineering impediment to realizing full connectivity: each qubit would need N − 1 physical couplers, and arranging such couplers spatially has proven to be impractical for large N. On the other hand, bus architectures have been demonstrated for superconducting-circuit qubits in the context of circuit-model quantum computing^11,12,13, and bus-mediated interactions naturally provide all-to-all coupling^11,14,15, with the use of one physical coupler per qubit. In this paper, we address the challenge of realizing full programmability of these all-to-all couplings, in the context of developing a quantum annealer.

In classical neuromorphic computing, a scheme providing full programmability has been proposed in an all-to-all-coupled system of Kuramoto oscillators using periodic modulation of each oscillator’s phase¹⁶. Separately, it has long been known that two quantum oscillators can be coupled via phase modulation at their difference frequency¹⁷. In much more recent work, nonlinear-oscillator-based qubits, whose operation relies on the continuous-variable nature of the oscillators, have been established as a promising building block for the realization of superconducting-circuit quantum annealers, owing partially to their resilience to photon loss^18,19,20. We take inspiration from all of these lines of work, and show how we can combine them to design a quantum annealer that comprises a system of nonlinear-oscillator-based qubits having all-to-all coupling mediated by a bus, where periodic modulation of the oscillators is used to provide programmability in the couplings. Our main technical contribution is in showing how, through careful design of the modulation of each oscillator’s instantaneous frequency, it is possible to enable full programmability, i.e., the realization of arbitrary connectivity between the qubits. We utilize the mathematical tools of Floquet theory^21,22 to formulate and solve the design problem of engineering the desired interactions between oscillators, and we establish that the functionality of our dynamically coupled system is equivalent to that of a statically coupled system with pairwise physical couplers. We show that to gain arbitrary connectivity in our scheme, one needs to trade off the strength of the effective couplings, the main consequence of which is that longer coherence times are needed.

Our scheme applies generically to a variety of nonlinear oscillators, including those realized in platforms besides superconducting circuits, such as optics^23,24,25,26 or nanomechanics^27,28. However, for concreteness, we focus on Kerr parametric oscillators^18,29,30 in which the Kerr nonlinearity is provided by a Josephson junction—i.e., Josephson parametric oscillators (JPOs)^{19,30,31,32,33,34}. JPOs have been utilized in two other schemes for achieving programmable couplings: a proposed realization²⁰ of the LHZ architecture³⁵ (which requires N(N − 1)/2 physical qubits to represent N spins), and an inductive-shunt scheme¹⁹ (which only provides ${\mathcal{O}}(N\mathrm{log}\,N)$ programmable parameters, out of a total of ${\mathcal{O}}({N}^{2})$ in general).

In summary, the previously known approaches to building a quantum annealer with JPOs are, variously, incompatible with dense connectivity due to engineering limitations; requiring of a large overhead in the number of qubits and/or couplers (i.e., scaling with N²); or lacking full programmability. In contrast, our proposal uses a bus to provide all-to-all connectivity and a dynamical approach to coupling that enables full programmability of N-spin Ising problems using a number of oscillators and couplers linear in N, and at the reasonable cost of coherence-time requirements that scale approximately linearly in N for computationally interesting problem classes.

Results

In this paper, we study the design of a quantum annealer whose purpose is to solve the Ising optimization problem, defined as finding the N-spin configuration ${\sigma }_{i}\in \left\{-1,+1\right\}$ (i = 1, …, N) that minimizes the classical spin energy E(σ): = ∑_j≠iC_ijσ_iσ_j, where C is a symmetric real matrix. A choice of C specifies a problem instance to be solved, and C can be interpreted as the adjacency matrix of a graph whose vertices are spins and whose edges represent spin-spin interactions. In general, C can have ${\mathcal{O}}({N}^{2})$ non-zero entries. It is desirable for a quantum annealer to be fully programmable, such that there are no restrictions on the structure of C, and that the annealer not use more than N oscillators to represent a given N-spin problem, nor use more than ∝ N other physical components. In this paper, we show how this can be achieved using nonlinear oscillators in a bus architecture together with dynamically realized couplings designed via Floquet engineering.

Figure 1a shows an overview of our proposed architecture. The N nonlinear oscillators of the quantum annealer are coupled to a common (bus) resonator. If the center frequencies of the oscillators are sufficiently far-detuned from the bus resonance, then the bus mediates a photon-exchange interaction between any pair of oscillators. In particular, denoting the annihilation operator for the ith oscillator as ${\hat{a}}_{i}$, the bus mediates interactions that contribute terms of the form ${\hat{a}}_{i}^{\dagger }{\hat{a}}_{j}+{\hat{a}}_{i}{\hat{a}}_{j}^{\dagger }$ to the system Hamiltonian¹¹ which generically couples every oscillator to every other oscillator. Thus with N nonlinear oscillators coupled to a bus, we can implement all-to-all coupling. However, the couplings up to this point are not programmable. The principal result in this paper is that we can engineer complete programmability of all the couplings by phase-modulating the oscillators in a specific way.

Fig. 1: Achieving fully programmable all-to-all coupling in oscillator networks via phase modulation.

An implementation-independent overview of the architecture, showing an example with N = 5 oscillators each coupled to a common bus resonator and each driven by a set of phase modulation (PM) signals. As depicted in (a), each oscillator is modulated by up to N − 1 harmonics with frequencies kΛ for integers k < N. The amplitude of each harmonic for each oscillator is given by an element in a phase-modulation matrix F, an example of which is shown on the left side of (b) (times a factor of 100 for clarity). The color of the PM signal on each oscillator indicates with which other oscillator the PM causes an interaction: for example, the k = 1 harmonic PM applied to Oscillator 1 (shown in orange) causes it to couple with Oscillator 2, and the k = 2 harmonic PM applied to Oscillator 1 (shown in green) causes it to couple with Oscillator 3. When a signal potentially mediates coupling to two other oscillators (e.g., k = 2 for Oscillator 3), we color by the oscillator with the lower center frequency (larger oscillator index i); the signals colored gray are not applied as they would not create any useful couplings. As shown in the power spectral density (PSD) of the oscillators' canonical positions on the right side of (b), the oscillators have center frequencies spaced by Λ; thus each PM signal at frequency kΛ creates a primary sideband which overlaps in frequency with the center frequency of the neighbor k oscillators away. Taken together, the effect of these sideband interactions is to generate a desired effective Ising-coupling matrix (see the Supplementary Information for the matrix used in this example).

In our scheme, the oscillators are, to a good approximation, detuned from each other by multiples of a fundamental frequency Λ, such that the kth-nearest neighbor of any given oscillator is detuned from it by kΛ. Despite the presence of the bus, for Λ sufficiently large the oscillators are effectively uncoupled in the absence of modulation (by the rotating-wave approximation). To effect dynamical coupling, each oscillator is controlled with a phase modulation (PM) signal containing harmonics of Λ, such that the resulting sidebands of each oscillator overlap in frequency with the center frequencies of the other oscillators. More precisely, the ith oscillator is phase-modulated by $\delta {\phi }_{i}(t):=-\mathop{\sum }\nolimits_{k = 1}^{N-1}{F}_{i}^{(k)}\sin (k\Lambda t)$, which causes its instantaneous frequency ω_i(t) to pick up a time-varying component ${\dot{\delta \phi }}_{i}(t)=-\mathop{\sum }\nolimits_{k = 1}^{N-1}{F}_{i}^{(k)}k\Lambda \cos (k\Lambda t)$. Here, the coefficients ${F}_{i}^{(k)}$ encode the strength of the kth-harmonic component in the PM of Oscillator i, and they can be summarized by a matrix F of dimension N × (N − 1) whose kth column consists of the elements ${F}_{1}^{(k)},\ldots ,{F}_{N}^{(k)}$. Intuitively, the strengths of the dynamically induced couplings are determined by the strengths of the sidebands, which in turn are controlled by the elements of F. Thus, the task of programming these couplings reduces to making an appropriate choice for F; we will present a method for choosing these coefficients shortly. Figure 1b is a cartoon depicting the realization of this PM scheme for a representative 5-spin problem instance; the coefficients ${F}_{i}^{(k)}$ are shown on the left, while on the right are the power spectral densities (PSDs) of each oscillator’s canonical position ${x}_{i}(t):=\cos(\mathop{\int}\nolimits_{0}^{t}{\omega }_{i}({t}^{\prime}){\rm{d}}{t}^{\prime})$. Each PSD shows a strong peak at its respective oscillator’s center frequency, together with sidebands of various amplitudes (controlled by F) that overlap with the center frequencies of the other oscillators.

While our method is independent of the exact type of nonlinear oscillator used, we specialize our discussion in this paper to a superconducting-circuits realization. For concreteness, we consider JPOs^19,30,31,33, although other superconducting-circuit-based oscillators are plausible choices as well^36,37. In the absence of coupling, the eigenstates of the JPO are 0-phase and π-phase coherent states^29,38; these two eigenstates can be used to encode, respectively, the spin-up and spin-down configurations of an Ising spin¹⁸, and superpositions of these eigenstates (i.e., Schrödinger cat states) have been experimentally demonstrated³³. Figure 2a shows N JPOs coupled to a superconducting resonator, which acts as the bus in this platform. Energy is supplied to each JPO by a flux line carrying a time-varying current. Conventionally, the dc component of the current determines the center frequency of the JPO, and an ac component at twice that frequency provides the parametric drive. In our scheme, the center frequency of each JPO is additionally modulated in time by $\dot{\delta \phi }(t)$, which is achieved by an additional modulation of the flux-line current corresponding to $\dot{\delta \phi }$^39,40. (In an alternative technological realization using a system of optical oscillators, this PM could potentially be applied by a physical phase modulator.)

Fig. 2: A superconducting-circuits implementation of the dynamical-coupling architecture.

a Josephson parametric oscillators (JPOs), whose frequencies can be modulated by a flux line, are coupled via a common microwave bus resonator. b Quantitative overview of the scheme for a JPO system, using the modulations shown in Fig. 1b and depicting the instantaneous angular frequencies ω_i(t) of the JPOs, both in the time domain (left) and as a PSD of ω₁ in the frequency domain (right). The PM signals manifest as modulations in the instantaneous frequency of each JPO, or, equivalently, in the detuning Δ_i(t) between the bus and Oscillator i. In the PSD, the PM signal appears in a low-frequency band (<0.5 GHz), while the parametric drive to the JPO (at twice the JPO’s frequency) occurs as usual in a high-frequency band ~ 20 GHz^19,30. The parameters used for the calculation of numerical quantities in (b) are from the bus-coupled JPO model described in the Supplementary Information.

For this JPO realization of a nonlinear-oscillator-based quantum annealer, Fig. 2b shows a more quantitative picture of our dynamical-coupling scheme, with plots of the instantaneous angular frequencies ω_i(t) both in the time domain (for all the oscillators) and in the frequency domain (for the first oscillator only). First, on the time-domain plot, we see that the effect of the PM is to create oscillations in the instantaneous detuning Δ_i(t) between the fixed bus resonance frequency and ω_i(t); in the absence of these modulations (or on time-averaging), the oscillator frequencies are approximately evenly spaced. As expected, the PM consists of four harmonics; looking at the frequency-domain plot, we see that these harmonics lie in a "coupling band” with frequency content ≪ 1 GHz. These plots also illustrate two more technical features specific to our construction (see the Supplementary Information for more information). First, the deviations in oscillator frequency from the center (i.e., the modulation depths) are small compared with the mean values of the bus-oscillator detunings; this qualitative feature ensures that the native couplings J_ij are approximately time-independent despite the PM. Second, there is a significant gap between the coupling band and the "pumping band” in which the parametric drive is realized; because of this separation of time scales, we can first design the flux-line currents to support the PM needed for dynamical coupling, while the parametric drive simply follows that modulation as needed. Since the ac part of the flux-line current is directly proportional to the ac part of ω_i(t) (see the Supplementary Information), we see that the entire control signal only requires ~20 GHz of bandwidth at most, which is realizable with current microwave technology.

We have thus far not explained how to choose the modulation coefficients F for a given problem instance C. An intuitive, but incorrect, choice is to simply set ${F}_{i}^{(k)}\propto {C}_{i,i+k}$, since generating a sideband at frequency kΛ on Oscillator i intuitively causes it to interact with Oscillator i + k. However, this is not entirely accurate, as the symmetrically generated sideband at − kΛ (caused by the same ${F}_{i}^{(k)}$ coefficient) also leads to the same interaction with Oscillator i − k; for arbitrary C, these two interactions may need to differ in general. Furthermore, we must also consider higher-order sidebands as well: even if we were to only phase modulate Oscillator i at frequency kΛ, weaker sidebands at ±2kΛ, ±3kΛ, and so on are also generated, causing interactions with Oscillators i ± 2k, i ± 3k, and so on, respectively. Thus, there is a nontrivial relation between F and the desired couplings C, and F needs to be chosen in a way such that the various contributions of F to the effective couplings among oscillators combine appropriately to give the desired couplings C. To do this formally, we apply the mathematical tools of Floquet theory^21,22.

First, to more explicitly define the problem we are trying to solve, a quantum annealer based on JPOs can be described by a (rotating-frame) Hamiltonian of the form^18,30

$$\begin{array}{l}{\hat{H}}_{{\rm{static}}}:=-\sum\limits _{i}({\delta }_{i}{\hat{a}}_{i}^{\dagger }{\hat{a}}_{i}+\frac{\chi }{2}{\hat{a}}_{i}^{\dagger 2}{\hat{a}}_{i}^{2})\\ \qquad\qquad\;+\sum\limits _{i}\frac{r(t)}{2}({\hat{a}}_{i}^{2}+{\hat{{a}_{i}}}^{\dagger 2})-{\lambda }_{{\rm{C}}}\sum\limits _{j\ne i}{C}_{ij}{\hat{a}}_{i}^{\dagger }{\hat{a}}_{j},\end{array}$$

(1)

where χ is the Kerr nonlinear rate, δ_i is the detuning between Oscillator i and the half-harmonic of its parametric drive, and r(t) is the (slowly time-varying) amplitude of the parametric drives. In this work, we choose the detuning to be ${\delta }_{i}={\lambda }_{\text{C}}\mathop{\sum }\nolimits_{j = 1}^{N}| {C}_{ij}|$ as prescribed by Ref. ¹⁸, and the parametric drive to be a clamped linear ramp $r(t)={r}_{\max }\min (t/{T}_{\text{ramp}},\ 1)$. Here, λ_C is a problem-strength parameter dictating the strength of the oscillator-oscillator couplings C_ij (which are normalized in this work to ${\max }_{j\ne i}| {C}_{ij}| =1$). One way to realize such a Hamiltonian is to have ${\mathcal{O}}({N}^{2})$ physical pairwise couplers, which can be programmed given a desired C_ij; these programmed couplings can then be held static throughout the annealing process while the parametric drive is varied.

By contrast, our goal is to realize this annealing Hamiltonian via dynamical control of the effective couplings among the oscillators. As a result, we start instead with the (rotating-frame) Hamiltonian (see the Supplementary Information for a derivation)

$$\begin{array}{ll}{\hat{H}}_{\text{dynamical}}:=-\sum\limits _{i}({\delta }_{i}{\hat{a}}_{i}^{\dagger }{\hat{a}}_{i}+\frac{\chi }{2}{\hat{a}}_{i}^{\dagger 2}{\hat{a}}_{i}^{2})+\sum\limits _{i}\frac{r(t)}{2}({\hat{a}}_{i}^{2}+{\hat{{a}_{i}}}^{\dagger 2})\\ \qquad-\sum\limits _{j\ne i}{J}_{ij}\exp \left[-{\rm{i}}(\Lambda (i-j)t+\delta {\phi }_{j}(t)-\delta {\phi }_{i}(t))\right]{\hat{a}}_{i}^{\dagger }{\hat{a}}_{j},\end{array}$$

(2)

which is the same as ${\hat{H}}_{\text{static}}$ with the exception of the final coupling term. In this case, J_ij are the bus-mediated coupling rates natively present in the system but which are not fully programmable in general (see the Supplementary Information for the exact form). By detuning the oscillators relative to one another by multiples of Λ and applying PM to the oscillators according to δϕ_i(t), the result is the “native” coupling term ${\hat{H}}_{\text{native}}:=-{\sum }_{j\ne i}{J}_{ij}\exp \left[-{\rm{i}}(\Lambda (i-j)t+\delta {\phi }_{j}(t)-\delta {\phi }_{i}(t))\right]{\hat{a}}_{i}^{\dagger }{\hat{a}}_{j}$. The time-varying phase factor is due to the PM of the Λ-detuned oscillators, and control over its time dependence forms the core of our dynamical-coupling scheme.

If we denote the coupling term in the static annealing Hamiltonian (1) as ${\hat{H}}_{\text{target}}:=-{\lambda }_{\text{C}}{\sum }_{j\ne i}{C}_{ij}{\hat{a}}_{i}^{\dagger }{\hat{a}}_{j}$, then the goal is to achieve ${\hat{H}}_{\text{native}}\approx {\hat{H}}_{\text{target}}$, under some appropriate sense of the approximation. As previously mentioned, we choose the modulations to be $-\mathop{\sum }\nolimits_{k = 1}^{N-1}{F}_{i}^{(k)}\sin (k\Lambda t)$, which means that ${\hat{H}}_{\text{native}}$ is periodic with frequency Λ. If Λ is much larger than all other system timescales, then the results of Floquet theory allow us to make the Floquet approximation ${\hat{H}}_{\text{native}}\approx -{\lambda }_{\text{C}}{\sum }_{j\ne i}{{C}_{\text{eff}}}_{ij}{\hat{a}}_{i}^{\dagger }{\hat{a}}_{j}$ where

$${{C}_{\text{eff}}}_{ij}:=\mathop{\int}\nolimits_{0}^{2\pi /\Lambda }\ \frac{{J}_{ij}}{{\lambda }_{\text{C}}}\cos \left[(i-j)\Lambda t+\mathop{\sum }\limits_{k=1}^{N-1}\left({F}_{i}^{(k)}-{F}_{j}^{(k)}\right)\sin (k\Lambda t)\right]\frac{{\rm{d}}t}{2\pi /\Lambda }$$

(3)

describes the effective couplings between oscillators i and j due to all the sideband interactions. (More formally, this approximation is the leading-order term in the Floquet-Magnus expansion of ${\hat{H}}_{\text{native}}$ in 1/Λ.) Thus, all that remains is to choose the coefficients in F such that ${{C}_{\text{eff}}}_{ij}\approx {C}_{ij}$. As discussed in the Supplementary Information, while it is possible to solve for F by direct numerical nonlinear optimization, there are a number of ways to make this precomputation step more tractable and robust. In particular, one can consider a second-order Taylor expansion of ${{C}_{\text{eff}}}_{ij}$ (intuitively, by considering effective interactions only up to the second-order sidebands) and obtain a system of quadratic equations that can be numerically solved.

To demonstrate the effectiveness of our approach, we perform numerical simulations of both the statically coupled system governed by ${\hat{H}}_{\text{static}}$ as well as the dynamically coupled system governed by ${\hat{H}}_{\text{dynamical}}$ (with an appropriate choice of F given C), and we show that they achieve nearly indistinguishable results, as one would expect if one has achieved ${\hat{H}}_{{\rm{dynamical}}}\approx {\hat{H}}_{{\rm{static}}}$. Figure 3a shows the results of simulating the quantum evolution of both systems as they perform quantum annealing on a two-spin problem, where the coupling between the spins is antiferromagnetic (Table 1). The joint quantum states of the dynamically coupled oscillators show that the system is initially in a vacuum state (with equal probability on each of the four possible spin configurations); by the end of the evolution, the system is in a superposition $\frac{1}{\sqrt{2}}\left(\left|\uparrow \downarrow \right\rangle +\left|\downarrow \uparrow \right\rangle \right)$ in the qubit basis, and would produce one of the correct ground-state spin configurations ↑↓ or ↓↑ upon measurement. We see that the evolution of the success probability to obtain a ground state is nearly identical for both architectures at all times, suggesting that the dynamically coupled system is closely mimicking the behavior of the statically coupled system, as desired.

Fig. 3: Quantum simulations.

a, b Evolution of the success probability of finding a ground state of the inset Ising problem instances, for both a system whose couplings are implemented by static pairwise physical couplers (static coupling) and a system using this work's dynamical-coupling approach (dynamical coupling), in the case of no dissipation. Shown to the bottom of (a) are the joint quantum states of the oscillators (represented as probability distributions ∣ψ(x₁, x₂)∣² and ∣ψ(p₁, p₂)∣² in canonical position and momentum coordinates, respectively) at three different times for the dynamically coupled system. c The probabilities of obtaining each of the possible spin configurations (i.e., configuration probability) as a function of the evolution time, for the problem instance and simulations shown in (b). Since the problem does not have any external fields, each spin configuration shown is degenerate to flipping every spin; for brevity, we have added together the probabilities corresponding to these degenerate configurations. d Correlation matrices of success probabilities P_success (evaluated at the end of the computation) between the statically coupled and dynamically coupled systems, for 100 instances of the SK7 problem class. (For the trajectory simulation data used to generate these correlation matrices, see the Supplementary Information.) Here, we also introduce a nonzero cavity-photon decay rate κ, to show that the correlations are high even in the presence of photon losses. Projected to the sides in blue and red are the corresponding histograms for the dynamically coupled and statically coupled systems, respectively. For simulation parameters and methodology, see Table 1 and “Methods”.

Figure 3b shows the same evolution of the success probability for a particular N = 4 problem instance, chosen from the class of finite-range, integer-valued Sherrington-Kirkpatrick (SK) instances studied in a foundational quantum-annealing benchmark work⁴¹; in particular, we utilize range-7 graphs (SK7) (see the Supplementary Information for details about instance generation). We again see that the evolutions of the success probabilities match very closely. Aside from the success probability, Fig. 3c shows the projections of the quantum state onto the spin configurations (of which there are 16 for N = 4), which demonstrates that the two architectures produce nearly indistinguishable evolutions in the projections as well.

In Fig. 3d, we show the results from N = 4 simulations for 100 different randomly generated problem instances (again drawn from the SK7 problem class). We simulate both the statically coupled and dynamically coupled quantum annealers and show the correlations between their respective success probabilities. To explore the effects of decoherence due to photon loss, we also examine these correlations for three different values of cavity-photon decay rate κ (which is related to the cavity-photon lifetime as T_cav: = 1/κ). We see that even in the cases of non-zero loss (κ > 0), both annealers are still able to find ground states with high success probability, which demonstrates the loss-resilience results found in previous work^19,20. Just as importantly, the correlations remain strong in the presence of photon losses. As a result, the loss resilience of the statically coupled architecture carries over to the dynamically coupled architecture, and even for those instances where the statically coupled system suffers in success probability due to photon loss events, the dynamically coupled system follows its behavior as expected.

While it would be desirable to validate our theoretical results with quantum simulations having more than N = 4 spins, full quantum simulations are prohibitively expensive for N > 4. Fortunately, for an oscillator-based quantum-optical system, there is a natural set of classical equations of motion (EOMs) which one can derive from the quantum model; formally, this consists of replacing the annihilation operators ${\hat{a}}_{i}$ with coherent-state amplitudes ${\alpha }_{i}\in {\mathbb{C}}$ in the quantum Heisenberg EOMs. Such a set of classical EOMs does not fully capture the dynamics of the system in the quantum regime, but we can nevertheless simulate these classical EOMs for both the statically coupled and dynamically coupled annealers and compare their dynamical behavior. If the two systems correspond well, we gain further confidence that our theoretical results can lead to the desired performance on a dynamically coupled quantum annealer. Figure 4 shows the results of simulating these classical EOMs for both architectures on SK7 problems. Figure 4a shows the evolutions of the success probabilities for a particular N = 10 problem instance, while Fig. 4b shows the evolutions of the field amplitudes α_i(t). We see that both the success probabilities and the oscillator amplitudes of the two architectures match well. Figure 4c shows the distribution of success probabilities for different problem sizes N up to N = 50, using 100 problem instances for N ≤ 30, and 30 instances for N = 50; the corresponding correlation plots for N = 8 and N = 30 are also shown to the bottom of the figure (additional correlation plots can be found in the Supplementary Information). There is good agreement between the simulation results of the statically and dynamically coupled systems: the success probability as a function of N scales in the same way, and the correlation plots show similar performance on an instance-by-instance basis.

Fig. 4: Simulations of classical equations of motion.

a Evolution of the success probability of finding a ground state of the inset 10-spin Ising problem instance, for both a system whose couplings are implemented by static pairwise physical couplers (static coupling) and a system using this work's dynamical-coupling approach (dynamical coupling). To estimate the probability, we sample random initial conditions according to a Gaussian distribution (see the Supplementary Information, ref. ¹⁸). b Trajectories of the classical field amplitudes of each of the 10 oscillators, for one of the samples constituting the simulation in (a). c Histograms of the success probability P_success for various problem sizes N, each estimated using 100 instances of the SK7 problem class. The diamonds indicate the average success probability, while the horizontal bars show the histogram. For N = 8 and N = 30, the correlation matrices between statically and dynamically coupled systems are shown at the bottom (For the correlation matrices for all other problem sizes, see the Supplementary Information). Projected to the sides of the correlation matrices, in blue and red, are the corresponding histograms for the dynamically coupled and statically coupled systems, respectively. For simulation parameters and methodology, see Table 1 and “Methods”.

Having shown that the dynamically coupled system indeed reproduces the behavior of the desired quantum annealer, we now discuss an important tradeoff inherent in our PM scheme for dynamical coupling. Examining the expression (3) for C_eff, we see that a key parameter is the ratio between the native couplings J_ij and the desired problem-strength parameter λ_C. For simplicity, we design the bus-resonator interactions in such a way that the native couplings are approximately constant (see the Supplementary Information for more details). Thus, let us assume that J_ij ≈ λ_J, where λ_J > 0 characterizes the rate at which photons are exchanged via the bus (i.e., the strength of the native couplings).

Under this framework, we can identify a "dynamical-coupling parameter” η: = λ_C/λ_J, which, intuitively, captures the "cost” of the dynamical-coupling scheme as it sets the scale for how much effective coupling we obtain for a given amount of native coupling provided to the scheme. As we discuss later, the absolute scale of λ_J is generally hardware-limited, while for any given problem, there is a fixed value of λ_C/χ required to ensure successful annealing (see the Supplementary Information for details). Given these constraints, larger values of η allow for larger operating values for χ, which is advantageous in the presence of a fixed cavity-photon lifetime. (A full account of the hierarchy of timescales and the chain of parameter requirements is given in the Supplementary Information.) Therefore, it is desirable to use as high a value of η as possible.

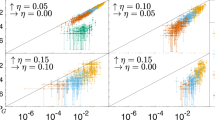
On the other hand, a clear requirement for dynamical coupling to work well is the ability to obtain C_eff ≈ C (so that ${\hat{H}}_{\text{dynamical}}\approx {\hat{H}}_{\text{static}}$) for any desired C. When η becomes large, however, the prefactor J_ij/λ_C ≈ 1/η in (3) becomes small. As discussed in the Supplementary Information, this effect can become detrimental to our ability to obtain C_eff ≈ C: intuitively, the maximum magnitude of the elements of C is by construction unity, but for a sufficiently small prefactor for the integral (i.e., sufficiently small 1/η), it becomes impossible to find a suitable set of coefficients ${F}_{i}^{(k)}$ that could allow the integral over the cosine to compensate. This phenomenon is demonstrated in Fig. 5. Given a particular target coupling matrix C, Fig. 5a shows, over a range of values for η, the C_eff matrices corresponding to the optimal F matrix found by our (second-order-Taylor-expansion-based) numerical routine (see the Supplementary Information). We see that when η is chosen to be too large, the correspondence between C and C_eff is rather poor. However, by decreasing η, one can achieve improved accuracy. More quantitatively, Fig. 5b shows the maximum element-wise error $({\max }_{i\ne j}| {{C}_{\text{eff}}}_{ij}-{C}_{ij}| )$, as a function of η and problem size N (averaged over an ensemble of 100 instances for each N). To show how the resulting error depends on the structure of C, we consider three problem classes: the SK7 class discussed above, the class of unweighted MAX-CUT problems with 50% edge density, and the class of unweighted MAX-CUT problems on cubic graphs (see the Supplementary Information for details about instance generation). As expected from our intuition about the role of η, the particular scaling of the error with η depends on the type of problems considered: for SK7, the required η goes approximately as η ∝ 1/N, while for dense MAX-CUT, $\eta \propto 1/(N\mathrm{log}\,N)$; in contrast with these two dense problem classes, cubic MAX-CUT problems require $\eta \propto 1/\mathrm{log}\,N$. From this figure, we see that, assuming we can tolerate an upper limit for the error in C_eff (say, of 3%), there is a maximum value for η that we are able to use for any given N. By staying below this maximal value, we can ensure feasible solutions for the modulation coefficients ${F}_{i}^{(k)}$ which generate effective couplings to within the acceptable error. In the Supplementary Information, we derive for each problem class an explicit, functional form of η with respect to problem size N such that we are guaranteed an error of at most 3%, but which is also not so conservative that the resulting nonlinear rate χ is unnecessarily low.

Fig. 5: Accuracy of the effective couplings.

a Comparison of the effective coupling matrices C_eff (target Ising problem matrix C shown to the left) for different settings of the dynamical-coupling parameter η, which sets the ratio between the effective coupling strength and the strength of the native coupling provided via the bus. As η is decreased, the accuracy of the C_eff increases. b The maximum entry-wise error in the effective coupling matrix C_eff, averaged over 100 problem instances for each size N, as a function of the dynamical-coupling parameter η. We show the scaling for three different classes of Ising problems, with illustrative examples of instances shown as insets. For all panels, the modulation matrix F used to produce C_eff is found by a numerical optimizer that attempts to maximize the accuracy by using a second-order Taylor approximation to (3), with native couplings J_ij constructed to be approximately uniform (see the Supplementary Information).

Finally, to study the technological feasibility of our dynamical-coupling scheme, it is important to understand how this tradeoff between the accuracy of the effective couplings and the nonlinear rate—in combination with the requirements for the Floquet approximation—translate into concrete scaling requirements for hardware figures of merit as a function of problem size. As previously mentioned, two relevant hardware limitations are the maximum coupling rate ${g}_{\max }$ between each oscillator and the bus, as well as the maximum realizable detuning ${\Delta }_{\max }$ between the bus and each oscillator. In the presence of these two limitations, we find (see the Supplementary Information for a full analysis) that there is a maximum allowable nonlinear rate ${\chi }_{\max }$ for dynamical coupling to work.

In Fig. 6a, we show ${\chi }_{\max }$ as a function of problem size N, upon varying the hardware limits ${g}_{\max }$ and ${\Delta }_{\max }$ (for the SK7 problem class; see the Supplementary Information for MAX-CUT). We observe that at fixed values of ${g}_{\max }$ and ${\Delta }_{\max }$, ${\chi }_{\max }$ decreases as N increases. To more concretely interpret the implications of the requirement $\chi \le {\chi }_{\max }$, we note that κ ≪ χ is a necessary condition for the annealer to operate in the quantum, rather than the dissipative, regime. Thus, the requirement of $\chi \le {\chi }_{\max }$ translates directly to a minimum required value for the cavity-photon lifetime T_cav = 1/κ. Taking κ = χ/5 for concreteness, we plot the minimum required cavity-photon lifetime T_cav on the right axis of Fig. 6b as a function of N, for ${g}_{\max }/2\pi =$20 MHz and ${\Delta }_{\max }/2\pi =$5 GHz. This plot indicates that T_cav ≈ 100 μs is required to achieve N = 1000.

Fig. 6: Scaling requirements for SK7 problems.

Due to the tradeoff between accuracy of the effective couplings and the required strength of native couplings, hardware limitations on the achievable bus-oscillator detunings and bus-oscillator couplings impose a maximum allowable nonlinear rate χ in the system. a The maximum allowable nonlinear rate as a function of the desired problem size N and the hardware-limited bus-oscillator coupling rate ${g}_{\max }$ (left, with ${\Delta }_{\max }/2\pi =5$ GHz) and the hardware-limited bus-oscillator detuning ${\Delta }_{\max }$ (right, with ${g}_{\max }/2\pi =20$ MHz). Dashed vertical lines in blue indicate the slice of these plots shown in (b) below. b The black line (left axis) shows the maximum allowable nonlinear rate as a function of problem size for fixed ${\Delta }_{\max }/2\pi =5$ GHz and ${g}_{\max }/2\pi =20$ MHz. The green line (right axis) shows the consequence of the maximum allowable nonlinear rate for the minimum required cavity-photon lifetime T_cav, assuming that the quantum annealer requires χ ≥ 5κ. See the Supplementary Information for the corresponding scaling requirements for MAX-CUT problem classes.

The values for ${g}_{\max }$ and ${\Delta }_{\max }$ are readily achievable experimentally; regarding the T_cav requirement, transmon qubits with T₁ times of around 50 μs–100 μs have been measured^42,43. We also mention that, in the spirit of refs. ^3,8, one could also ignore this latter requirement on T_cav and build a system with the best T_cav one can achieve—even if it is smaller than the required T_cav to satisfy κ ≤ χ/5—and experimentally explore the performance of a highly dissipative quantum annealer. For a small experimental demonstration that still obeys the κ ≤ χ/5 requirement, T_cav ~ 10 μs should be sufficient to realize an N = 10 version of the system.

Discussion

There are two fundamental tradeoffs that one is making by adopting our dynamical-coupling architecture versus a static-coupling architecture: firstly, it is necessary to perform some classical precomputation to obtain the PM coefficients (i.e., the matrix F), and secondly, as alluded to in the discussion about the dynamical-coupling parameter η, each oscillator’s cavity-photon lifetime in a dynamical-coupling architecture will need to be longer than it would in a static-coupling architecture. In exchange for accepting these two downsides, one is able to build a fully programmable, fully connected N-spin quantum annealer with a number of qubits and couplers that only scales as N, as opposed to current proposals for statically coupled quantum annealers, which require a number of qubits and/or couplers that scales as N².

Our method for computing F—by minimizing a second-order Taylor approximation of effective coupling error—requires only ${\mathcal{O}}({N}^{3})$ time, which is efficient, and remarkably so given that the Ising problem matrix contains ${\mathcal{O}}({N}^{2})$ entries in general, hence the runtime could at best be ${\mathcal{O}}({N}^{2})$. Moreover, in our numerical experiments, the wall-clock times when running our implementation of the method on a single-core processor were ~2 min for N = 1000, so the precomputation time should not be a significant practical concern, given the difficulty of solving hard instances of Ising problems.

With regards to the required cavity-photon lifetime, we have provided (in the Supplementary Information) a prescription for the parameters in the dynamical-coupling scheme such that the error in the realized couplings will be at most ~3%, and we have computed the resulting cavity-photon-lifetime requirement as a function of N. Current experimental efforts with JPOs^33,34 have shown promising development. In particular, a single cat qubit with a JPO was demonstrated in Ref. ³⁴, and the qubit had T₁ and T₂ values of 15.5 μs and 3.4 μs respectively. While the use of dynamic flux modulation to induce multimode couplings among JPOs (with or without a bus) has not yet been experimentally investigated to the best of our knowledge, flux modulation has been used to construct two-qubit gates between transmon qubits⁴⁰ as well as to couple multiple modes of a transmission line⁴⁴. Meanwhile, bus-mediated multi-qubit couplings achieving all-to-all entanglement have now reached the scale of up to 20 transmon qubits on a single chip¹⁵. These experimental milestones, together with the generally rapid progress in superconducting circuit hardware, indicate that the coherence-time requirements found in our scaling analysis—10 μs for a small-scale near-term demonstration and 100 μs for a 1000-spin machine—are within optimistic experimental reach.

In the current approach from D-Wave Systems^6,8,45, as well as the proposed approaches in refs. ^20,35, realizing a 1000-spin quantum annealer for fully connected problems would require on the order of 10⁶ qubits. This stands in contrast to our proposed architecture, which would require only 1000 oscillators to achieve the same number of spins. Beyond the engineering expense of implementing a relatively larger number of qubits, quantum annealers using problem embedding can also suffer from an additional exponential degradation in success probability⁶. The dynamical-coupling approach uses the minimal number of physical qubits possible, and hence avoids this additional penalty in performance.

Outside the context of quantum annealing for solving optimization problems, our work has a strong connection with Floquet engineering of quantum simulators and quantum spin chains^{46,47,48,49,50}. A quantum annealer, in addition to being an optimization machine, is also a realization of a quantum simulator of the transverse-field Ising model⁵¹. We anticipate that our techniques for dynamic control of the couplings in a spin system will also enable the realization of novel simulation capabilities for more general spin Hamiltonians. Furthermore, our technique and derivations are not restricted to simulators of spin systems, but apply directly to generic bosonic simulators, and may allow more complex Hamiltonians to be engineered than are currently realized with pairwise physical couplers in Bose-Hubbard simulators built with superconducting circuits^{52,53,54,55,56}.

Methods

Ising problem classes and problem instance generation

We consider problem instances drawn from the following three specific classes of Ising problems, characterized by the statistical distribution of the C_ij couplings specifying the Ising problem:

• Integer Sherrington-Kirkpatrick graphs with range 7 (SK7)⁴¹: Every upper-triangular element of C is independently chosen with equal probability from 14 discrete values $\left\{-7,\ldots ,-1,1,\ldots ,7\right\}$. Then C is normalized by its maximum amplitude: $C\mapsto C/{\max }_{ij}(| {C}_{ij}| )$.

• Dense MAX-CUT graphs: Every upper-triangular element of C is independently chosen with 50% probability to be either 0 or 1.

• Cubic MAX-CUT graphs: We sample uniformly from the set of 3-regular graphs, where every vertex has degree 3. These graphs were generated with the LightGraphs.jl package⁵⁷.

Solving for modulation coefficients

The problem of finding the matrix of modulation coefficients F is to satisfy ${C}_{ij}\approx {{C}_{\text{eff}}}_{ij}$, as defined in (3). In a fully numerical approach, this problem can be solved by numerically minimizing the objective function

$$\sum _{i\ne j}{\left({\lambda }_{\text{C}}{C}_{ij}-\mathop{\int}\nolimits_{0}^{2\pi }{J}_{ij}\cos \left[(i-j)t+\mathop{\sum }\limits_{k = 1}^{N-1}\left({F}_{i}^{(k)}-{F}_{j}^{(k)}\right)\sin kt\right]\frac{{\rm{d}}t}{2\pi }\right)}^{2}.$$

(4)

For N < 100, we numerically optimize a relaxed version of this problem (using an iterative approach; see the Supplementary Information), which for these values of N provides low-error solutions.

For N > 100, the above procedure scales poorly with N, so we turn to an approximate approach. If we assume the total phase deviation $\mathop{\sum }\nolimits_{k = 1}^{N-1}\left[{F}_{i}^{(k)}-{F}_{j}^{(k)}\right]\sin (k\Lambda t) \sim \zeta$ where ζ ≪ 1 (i.e., the modulations are small), then the equation ${C}_{ij}={{C}_{\text{eff}}}_{ij}$ can be expanded to second order in ζ to obtain the equations

$$\begin{array}{ll}\frac{{\lambda }_{\text{C}}{C}_{ij}}{{J}_{ij}}&=-\frac{1}{2}\left({F}_{i}^{(i-j)}-{F}_{j}^{(i-j)}\right)-\frac{1}{8}\mathop{\sum }\limits_{l=1}^{N-1-(i-j)}\left({F}_{i}^{(l)}-{F}_{j}^{(l)}\right)\left({F}_{i}^{(i-j+l)}-{F}_{j}^{(i-j+l)}\right)\\ &\ \ -\frac{1}{8}\mathop{\sum }\limits_{l=i-j+1}^{N-1}\left({F}_{i}^{(l)}-{F}_{j}^{(l)}\right)\left({F}_{i}^{(l-i+j)}-{F}_{j}^{(l-i+j)}\right)\\ &\ \ +\frac{1}{8}\mathop{\sum }\limits_{l=1}^{i-j-1}\left({F}_{i}^{(l)}-{F}_{j}^{(l)}\right)\left({F}_{i}^{(i-j-l)}+{F}_{j}^{(i-j-l)}\right).\end{array}$$

(5)

An exact solution to these equations does not necessarily solve ${C}_{ij}={{C}_{\text{eff}}}_{ij}$, but the errors should be small if ζ ≪ 1. Since this small-modulation approximation significantly reduces the nonlinearity of the problem, we utilize this second-order approximation as our definition of the design problem to be solved when N ≥ 100. To solve the problem in this approximation, we again apply a relaxation to solve these algebraic equations via solving an optimization problem instead, with objective functions (one for each k = 1, …, N − 1):

$$\mathop{\sum }\limits_{j=1}^{N-k}{\left(\frac{{\lambda }_{\text{C}}{C}_{j}^{(k)}}{{J}_{j}^{(k)}}+\frac{1}{4}\left({F}_{j+k}^{(k)}-{F}_{j}^{(k)}\right)\left[2+{\theta }_{2k}^{N-1}\left({F}_{j+k}^{(2k)}-{F}_{j}^{(2k)}\right]\right)+{u}_{j}^{(k)}\right)}^{2},$$

(6)

where ${\theta }_{M}^{N}=1$ iff N ≥ M and

$$\begin{array}{ll}{u}_{j}^{(k)}:=\frac{1}{8}\mathop{\sum }\limits_{l=1}^{N-1-k}\left(1-{\delta }_{k,l}\right)\left({F}_{j+k}^{(l)}-{F}_{j}^{(l)}\right)\left({F}_{j+k}^{(k+l)}-{F}_{j}^{(k+l)}\right)\\ \qquad\quad +\frac{1}{8}\mathop{\sum }\limits_{l=k+1}^{N-1}\left(1-{\delta }_{2k,l}\right)\left({F}_{j+k}^{(l)}-{F}_{j}^{(l)}\right)\left({F}_{j+k}^{(l-k)}-{F}_{j}^{(l-k)}\right)\\ \qquad\quad-\frac{1}{8}\mathop{\sum }\limits_{l=1}^{k-1}\left({F}_{j+k}^{(l)}-{F}_{j}^{(l)}\right)\left({F}_{j+k}^{(k-l)}-{F}_{j}^{(k-l)}\right).\end{array}$$

(7)

Our approach is to iteratively optimize these objective functions one at a time, repeating until convergence or after a fixed number of optimizations have been performed. For additional information, see the Supplementary Information.

Quantum simulations

We perform quantum simulations in this work to analyze the performance of the dynamical-coupling scheme relative to the statically coupled system, especially in the presence of dissipation. Our dissipative quantum model is described by the standard Lindblad master equation

$$\frac{{\rm{d}}\hat{\rho }}{{\rm{d}}t}=-{\rm{i}}[\hat{H},\hat{\rho }]+\sum _{i}\left({\hat{L}}_{i}\hat{\rho }{\hat{L}}_{i}^{\dagger }-\frac{1}{2}{\hat{L}}_{i}^{\dagger }{\hat{L}}_{i}\hat{\rho }-\frac{1}{2}\hat{\rho }{\hat{L}}_{i}^{\dagger }{\hat{L}}_{i}\right),$$

(8)

where $\hat{H}$ is the Hamiltonian of the system, and ${\hat{L}}_{i}$ are the Lindblad operators that describe the effect of dissipation due to coupling to the environment; the time dependence of all operators has been omitted for brevity. For the statically coupled scheme, the Hamiltonian is given by (1) while the Lindblad operators are given by ${\hat{L}}_{i}=\sqrt{\kappa }{\hat{a}}_{i}$. For the dynamical-coupling scheme, the Hamiltonian is given by (2), while the Lindblad operators remain ${\hat{L}}_{i}=\sqrt{\kappa }{\hat{a}}_{i}$, since the terms in (8) involving the Lindblad operators are invariant under the overall frame rotations imposed by the dynamical-coupling scheme (see the Supplementary Information for more details).

Directly simulating (8) is difficult due to the large Hilbert-space dimension of the quantum state. To circumvent the memory requirement of storing a full density matrix, we utilize the Monte-Carlo wavefunction method (i.e., quantum-jump method) to solve (8) via stochastic sampling ⁵⁸. Numerically, the simulations were performed with the QuTiP library (version 4.3.1) in Python⁵⁹.

Given a spin configuration $\sigma =\left({\sigma }_{1},\ldots ,{\sigma }_{N}\right)$ where σ_i = ±1, we can define the probability of the quantum state $\hat{\rho (t)}$ being in the specific spin configuration (i.e., configuration probability) σ as¹⁸

$${\text{P}}_{\sigma}(t):=\mathop{\prod}\nolimits_{i=1}^{N}\left({\mathop{\int}\nolimits_{{\text{sgn}}\,{x}_{i}={\sigma}_{i}}}{\rm{d}}{x}_{i}\right)\left\langle {x}_{1},\ldots ,{x}_{N}\right|\hat{\rho (t)}\left|{x}_{1},\ldots ,{x}_{N}\right\rangle.$$

(9)

This definition of the success probability is motivated by the fact that the final state of the JPO system is approximately a superposition of coherent states $\left|\pm {\alpha }_{i}\right\rangle$ for each JPO, and we interpret these coherent states to encode the Ising spins σ_i = ±1.

Classical simulations

For the statically coupled system, we simulate the following classical EOMs:

$$\frac{{\rm{d}}{\alpha }_{i}}{{\rm{d}}t}={\rm{i}}\left({\delta }_{i}+\chi | {\alpha }_{i}{| }^{2}\right){\alpha }_{i}-{\rm{i}}r{\alpha }_{i}^{* }+{\rm{i}}{\lambda }_{\text{C}}\sum _{i\ne j}{C}_{ij}{\alpha }_{j}.$$

(10)

For the dynamically coupled system, we simulate the following classical EOMs:

$$\begin{array}{l}\frac{{\rm{d}}{\alpha }_{i}}{{\rm{d}}t}={\rm{i}}\left({\delta }_{i}+\chi | {\alpha }_{i}{| }^{2}\right){\alpha }_{i}-{\rm{i}}r{\alpha }_{i}^{* }\\ \qquad\,+\,{\rm{i}}{\lambda }_{\text{C}}\sum\limits _{j\ne i}{J}_{ij}\exp \left[-{\rm{i}}\Lambda (j-i)t+{\rm{i}}\delta {\phi }_{j}(t)-{\rm{i}}\delta {\phi }_{i}(t)\right]{\alpha }_{j}.\end{array}$$

(11)

We simulate both sets of classical EOMs using the ODE solver library DifferentialEquations.jl (version 4.5.0) in Julia⁶⁰. Regarding the initial conditions of the ODE, we follow the approach of Ref. ¹⁸ and sample random initial-field amplitudes α_i(t = 0), according to ${\alpha }_{i}(t=0)=\sqrt{{n}_{0}/2}\ {{\rm{e}}}^{2\pi {\rm{i}}{u}_{i}}{z}_{i}$, where z_i are iid random variables drawn from the standard normal distribution, while u_i are iid random variables drawn from the uniform distribution on the interval [0, 1]. For all classical simulations, we choose n₀ = 10⁻². As with the quantum simulations, we simulate the classical EOMs on a finite number of trajectories.

In our classical simulations, we identify the spin configuration of a trajectory α(t) using the relation ${\sigma }_{i}(t)={\rm{sgn}}\left({\rm{Re}}\ {\alpha }_{i}(t)\right)$. The spin configurations over the ensemble of trajectories then determine the success probability.

Table 1 System parameters of the statically and dynamically coupled annealers for representative quantum (left) and classical (right) simulations in this work.