Introduction

The structure of structural domains and the domain walls separating them is fundamental to the electrical transport properties of thin films1,2. Domain walls scatter the conduction electrons and contribute to the electrical resistance of a film at low temperatures where thermal scattering is reduced3. The prototype high-temperature superconductor material, La2-xSrxCuO4 (LSCO) has a structural phase transition between a low-temperature orthorhombic (LTO) phase and a high-temperature tetragonal (HTT) phase4. At a doping level of \(x=0.12\), which is close to the optimal doping for superconductivity, the structural phase transition lies around \({T}_{{\rm{S}}}=200{\rm{K}}\). Recently, an unusual transverse resistance has been discovered in devices created from atomic-layer epitaxial grown LSCO thin films5. The transverse resistance has a 2-fold orientation dependence on direction, uncoupled from the crystallographic directions, in the film despite the nominal 4-fold symmetry of its high-temperature structure. The epitaxial domains may be responsible for this symmetry breaking. Thus, imaging the nanoscale domain structure at an ultrafast timescale relevant for electron scattering using inversion of single-shot coherent diffraction patterns can provide essential clues on this. Phase retrieval (PR), a long-standing computational challenge, allows reconstructing a complex-valued image from the coherent diffraction pattern in reciprocal space. This is a common problem encountered in many coherent imaging techniques such as holography6, coherent diffraction imaging7 and ptychography8. In the last few decades, many approaches have been developed for solving the PR problem. The most popular method is based on alternative projection, initially proposed by Gerchberg and Saxton9 and extended by Fienup10,11. The alternating projection algorithm aims to recover the complex-valued image from the intensity-only measurement at the detector sensor plane. However, some of the projections involve non-convex sets. Hence, the algorithm becomes stuck in local minima12. Although other methods have been developed to overcome these limitations by using the tools of modern optimization theory, including semi-definite programming-based (SDP) approaches13,14,15, regularization-based methods16,17, global optimization methods18 and Wirtinger flow and its variants19, the computational complexity of these PR algorithms is large, and it is time-consuming to converge to a solution with high confidence.

Recently, deep learning based methods for the PR problems are becoming increasingly popular20,21,22. Once the trained model is obtained, the real-space complex-valued object can be recovered from its corresponding coherent X-ray diffraction pattern in milliseconds because of the no-iterative and end-to-end properties of deep learning-based methods. Thus, a large body of literature has leveraged the machine learning model to solve the PR problem in holographic imaging23, X-ray ptychography24, lensless computational imaging25, X-ray Free-electron Laser (XFEL) pulse imaging26, and Bragg coherent diffraction imaging (BCDI)27,28,29,30. Typically, deep learning based methods adopt the general encoder–decoder architecture, in which they first encode the input signal (e.g., the measured diffraction pattern) to a low-dimensional manifold feature space and then reconstruct the phase information only or both amplitude and phase information through one or two separate decoders. The amplitude and phase (or real and imaginary) information obtained from these coherent imaging methods has a certain physics relation between them. For example, the real and imaginary parts of the complex refractive index of a sample (revealed by a forward coherent diffraction imaging experiment) are intrinsic properties of its atomic distribution and are connected by the Kramers–Kronig relation. However, most previous works utilize real-valued neural networks for PR problems and consider the amplitude and phase (or real and imaginary) information of a sample as two independent outputs, the physical connection between them is weak.

In this work, we have invoked a complex-valued operation in a convolutional neural network (CNN) to take into account the connection between phase and amplitude. Specifically, we employed a complex-valued convolutional neural network (C-CNN) to recover the complex-valued images from the corresponding coherent diffraction patterns in reciprocal space. For experimental coherent diffraction data, we chose to look at an LSCO sample with \(x=0.07\) for which the HTT-LTO phase transition lies around \({T}_{{\rm{s}}}=330{\rm{K}}\) with an XFEL source, because there might be associated critical fluctuations reported in the previous work31,32. Therefore, the sample was measured on a vibration-free Peltier stage as a function of temperature near \(330{\rm{K}}\). One mechanism for observing these critical fluctuations would be by snapshot imaging of coherent diffraction patterns on the ultrafast time scale. We found that the C-CNN significantly outperforms the traditional real-valued CNN (R-CNN) on the synthetic data and achieved lower \({\chi }^{2}\) errors with the experimental XFEL data. With our developed C-CNN model, complex phase domains were observed with the coherent x-ray diffraction patterns on the ultrafast timescale measured from the LSCO sample. In addition, we also observed the characteristic signature of fluctuations in the real space recovered amplitude. These fluctuations, however, may be related to the beam pointing fluctuations rather than the critical fluctuations of the LSCO sample. The reconstructed snapshot images of the domains within the LSCO thin film roughly agree with expectations from the epitaxial growth conditions, showing as circular patches ~100 nm in diameter, each showing a different phase from its neighbors.

Results

XFEL experiment

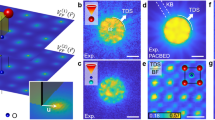
A classical picture of the expected structure of epitaxial thin films33 is shown in Fig. 1. Islands of the nucleating film material are locally lattice-matched to the substrate touching at domain walls, as shown in Fig. 1a, b. The local epitaxial forces cause the film domains to align with the substrate at their centers and the misfit builds up toward the domain walls. As a result, each domain of the thin film has a different registration of its crystal lattice with respect to the average film lattice. Consequently, the Bragg peak of the thin film is shifted in-plane from that of the substrate, as is commonly seen34. Importantly, the peak of the thin film is diffuse, broadened in-plane to a size mainly determined by the reciprocal of the domain size and broadened out-of-plane to a size given by the reciprocal of the film thickness, as shown in Fig. 1d. There are wide-ranging models of epitaxial growth of thin films on crystalline substrates summarized in Thompson’s review article33. Grain boundaries accommodate any misfit between the film and the substrate lattice constants as strain within the film. Because thin films usually have 2D arrays of domains, as we discuss below, this means that simple 2D coherent X-ray diffraction patterns of thin-film Bragg peaks contain all the information about the domain structure, which can therefore be revealed by phase retrieval.

Fig. 1: Domain structure expected due to misfit between a thin film and its substrate.
figure 1

a Initial stage of growth has islands locally registered with respect to the LSAO substrate. b In the frame of reference of the LSCO thin film’s crystal lattice, the resulting domains are phase shifted (indicated by \(\varphi\)) relative to each other. c Laboratory frame views of the side and top of the sample mounted on its wedge. d Corresponding side and top views of diffraction geometry. The incident (\({{\bf{k}}}_{{\rm{i}}}\)) and exit (\({{\bf{k}}}_{{\rm{f}}}\)) wave vectors and the wavevector transfer Q, lie in the horizontal scattering plane. The detector plane, perpendicular to \({{\bf{k}}}_{{\rm{f}}}\), is also inclined but still cuts across all the diffraction rods from the sample. e, f Two representative coherent diffraction patterns of the (103) Bragg peak of the sample. The solid ellipse marks the estimate peak width, and the dished ellipse shows the representative speckle size. All the scale bars are 20 \({{{\upmu }}{\rm{m}}}^{-1}\). g Schematic real-space picture of domains falling within the beam footprint (large ellipse) in the detector coordinate.

Full size image

A thin-film sample of LSCO (\(x=0.07\)) with a thickness of 75 nm was prepared by atomic-layer epitaxy on a LaSrAlO4 (LSAO) substrates and was measured at the Materials Imaging and Dynamics (MID) instrument of the European X-ray Free Electron Laser facility in Hamburg, Germany35. The incident X-ray beam of 8.8 keV photon energy was delivered from the self-amplified spontaneous emission (SASE) undulator through a double-crystal monochromator and compound refractive lens (CRL) focusing system onto the axis of a horizontal 2-circle diffractometer. The LSCO sample was pre-aligned to the (103) reflection by means of a 40° wedge shown in Fig. 1c, selected for the relatively large structure factor of LSCO. This Bragg peak was captured by the adaptive gain integrating pixel detector (AGIPD) situated 8 m downstream of the sample at a 2\(\theta\) angle of 29°. The crystal was then rotated to find the (103) reflections of the thin film in the bisecting geometry. The nearby (103) reflection of the LSAO substrate aided in the alignment procedure. Figure 1d shows the diffraction geometry in the reciprocal space coordinate system of the LSCO thin film. The diffraction features are enlarged for clarity. The (103) reflections have been drawn with an elliptical envelope shape of width given by the reciprocal of the size of one of the thin-film domains along the in-plane [H, 0, 0] direction; the width along the out-of-plane [0, 0, L] direction is the reciprocal of the film thickness. The speckles, have a width along [H, 0, 0] which is the reciprocal of the beam footprint size on the sample, but the same length along [0, 0, L] because the beam penetrates the whole film, and the domains are expected to have the same thickness as the film. These speckles extend in 3D above and below the plane shown in Fig. 1d, filling the volume of a prolate ellipsoid.

The diffraction triangle, defined by \({\bf{Q}}={{\bf{k}}}_{{\rm{f}}}-{{\bf{k}}}_{{\rm{i}}}\), is shown in Fig. 1d. The Ewald sphere, tangential to the tip of the \({{\bf{k}}}_{{\rm{f}}}\) vector, determines which parts of the 3D diffraction pattern are selected by the geometry. This is shown as an inclined box, representing the AGIPD plane, lying perpendicular to the \({{\bf{k}}}_{{\rm{f}}}\) vector and tangential to the Ewald sphere. The plane cuts across the speckles at a compound angle, so they should appear as tilted ellipses on the detector. The domain counting concept36 applies even in this tilted geometry. In each direction in the detector, the speckle size is the reciprocal of the beam size on the sample, while the dimension of the envelope ellipse containing the speckles is the reciprocal of the domain size. The ratio of these numbers, the number of speckles seen on the detector, is equal to the number of domains illuminated by the beam on the sample.

After adjusting the focus position of the CRL optics, speckles could be seen in the diffraction on the detector, and these were seen to vary from shot to shot. Time series data were collected with the sample at room temperature in a long run of 1002 pulse trains of 140 pulses at 2.2 MHz repetition rate, repeated every 100 ms, employing an X-ray attenuator with 33% transmission was used to prevent beam induced damage to the sample. Speckles could be seen in the images summed over the pulse trains and these had a different distribution from one train to another. Smaller fluctuations were identified between individual shots within the same pulse train. We performed a series of data cross-correlation studies to show that the patterns were repeating over the entire sequence, and we developed a clustering scheme (described in the Methods section) to generate 20 consensus diffraction patterns (see Supplementary Fig. 7 for the cross-correlation analysis).

Figure 1e, f shows two typical diffraction patterns viewed on the front face of the detector. Before inverting these diffraction patterns to images, we can learn a lot from the shape and distribution of the speckles, in consideration of the phase domain structures expected. As can be seen in Fig. 1f, the speckles have elliptical shapes with an elliptical envelope surrounding them. This is what we expected according to the discussion of the diffraction geometry above. The streaked, tilted elliptical shape of each speckle arises from their compound angle to the Ewald sphere, as seen in Fig. 1d. From the width of the speckles, estimated in Fig. 1f to be 1.5 pixels of 200 µm, we evaluate the beam size on the sample to be 3.7 µm. The domain dimensions can be estimated from the reciprocal of the larger ellipse in Fig. 1f which delineates the shape of the envelope surrounding the speckles; this hierarchical structure of the coherent diffraction pattern is precisely what is expected from ensembles of close-packed domains interfering with each other36. The major axis length is elongated by the tilting of the detector plane with respect to the envelope of the speckles seen in Fig. 1e, f. From the minor axis dimensions of the envelope ellipse, 46 pixels, we estimate that the domain size is 122 nm on average.

For inversion of the diffraction patterns to real space images by our C-CNN method, a set of reference images and diffraction patterns are needed to train the network. Between the random selection of domain positions and the choice of random phase shifts, attributed to the local epitaxial relation with the substrate (discussed above), there are plenty of degrees of freedom for generating many training data for the neural network. In the Synthetic data generation method section, elliptical-shaped domains are randomly placed within the larger elliptical envelope, shown in Fig. 1g, representing the beam footprint. The dimensions and the rotation of the two sets of ellipses are determined as the inverse of the dimensions of the reciprocal-space ellipses from Fig. 1f estimated to be 74 × 46 and 11 × 1.5 pixels for the large and small ellipses respectively. This picture is drawn in the real space coordinates of the Fourier transform of the detector data rather than the surface plane and is used to define the synthetic data model used for training. All results in this paper are presented in this detector coordinate system.

Complex-valued neural network architecture

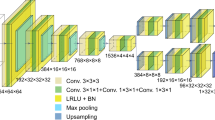
Figure 2a shows the architecture of the proposed C-CNN model utilized the classical encoder–decoder architecture37 with skip connection, composed of 2D convolutional, max-pooling and up-sampling layers. However, all operations in each layer (i.e., non-linear activation, convolution, max-pooling, and up-sampling) are performed based on the corresponding complex-valued operations, where each layer has two sub-layers separately accounting for the real and imaginary parts (see Supplementary Notes 1 and 3 for more details). Especially, Fig. 2b further shows the detailed operation of the complex-valued convolutional operation used in the C-CNN model, as marked by the yellow color in Fig. 2a. As presented, for each convolutional layer, the input and output size are \([{H}_{{\rm{k}}},{W}_{{\rm{k}}},2]\) with two channels (i.e., real and imaginary). These two channels are connected with each other through the complex-valued convolutional operation. For instance, the output’s real part contains both information from the input’s real and imaginary, and the real and imaginary kernels also multiply the input’s real and imagery simultaneously. When applying the model to the experimental data, we train the refined model with the output of the pre-trained complex-valued model as the input, the model can be further refined by continued training (with a Fourier transform constraint) in an unsupervised learning manner on the experimental data. We term it unsupervised learning for experimental data, since we do not have any ground truth in the real space, following similar usage in related works29,30. Continued training means that the model is first trained on simulated data with a ground truth, and then uses the pre-trained model’s output as the initialization for continued training the refined model with experimental data. Figure 2c demonstrates the detailed pipeline of the proposed C-CNN model using in this unsupervised learning framework30. Further details of the unsupervised learning framework with the experimental XFEL data are included in the “Performance on experimental XFEL data” section.

Fig. 2: Schematic illustration of our complex-valued neural network for phase retrieval.
figure 2

a Architecture of the C-CNN model. b Convolutional operation for complex number. The size of the complex-valued input is \([{H}_{\rm{I}},{W}_{\rm{I}},2]\), where \({H}_{\rm{I}}\), \({W}_{\rm{I}}\) is the height and width of input with two channels real (marked with green) and imaginary (marked with pink), respectively. The size of convolutional kernel is \([{H}_{\rm{k}},{W}_{\rm{k}},2]\), where \({H}_{\rm{k}},{W}_{\rm{k}}\) are corresponding height and width of kernel with two channels real (marked with blue) and imaginary (marked with pink), respectively. The size of output is \([{H}_{\rm{o}},{W}_{\rm{o}},2]\), obtained based on the convolutional of complex-valued input and corresponding complex-valued kernel. c Pipeline of the unsupervised learning for real experimental data. We employ the output of the pre-trained model on synthetic data as the starting point and continue the training with a Fourier transform constraint on experimental data.

Full size image

Performance on synthetic data

To demonstrate the performance and applicability of the proposed C-CNN model to the PR problem, we first apply the C-CNN model to the synthetic data in a supervised learning manner. Paired sets of diffraction patterns and object images are prepared for training the C-CNN model. In order to utilize the complex-valued neural network, we first set the phase of coherent diffraction patterns to \(\frac{{\rm{\pi }}}{4}\) and then use the calculated real and imaginary part of the obtained diffraction patterns as input for the model. Errors between the prediction of the C-CNN model and the corresponding target are quantified using the mean absolute error (MAE). As shown in Fig. 2a, the sizes of input and output are the same, which is \(N\times W\times H\times 2\), where \(N\) is batch size, \(W\) and \(H\) is the width and height of the input diffraction patterns. In this study, we set \(N=64\) and \(W=H=64\). The objective function is defined as:

$$L={L}_{{\rm{re}}}+{L}_{{\rm{im}}}=\frac{1}{N}\mathop{\sum }\limits_{{\rm{i}}=1}^{N}\left|{\hat{\rho }}_{{\rm{re}}}-{\rho }_{{\rm{re}}}\right|+\frac{1}{N}\mathop{\sum }\limits_{{\rm{i}}=1}^{N}\left|{\hat{\rho }}_{{\rm{im}}}-{\rho }_{{\rm{im}}}\right|,$$
(1)

where \({\hat{\rho }}_{{\rm{re}}}\) and \({\hat{\rho }}_{{\rm{im}}}\) correspond to the predicted real and imaginary parts of the object in real space, \({\rho }_{{\rm{re}}}\) and \({\rho }_{{\rm{im}}}\) are the real and imaginary components of the ground truth in real space, respectively. Supplementary Note 5 and Supplementary Fig. 2 provide details of the training process and learning curve on simulated data, showing that the C-CNN converged well at about 500 epochs.

To fairly compare with R-CNN, we select the same number of layers and the number of filters for each layer for both complex-valued and real-valued neural networks on synthetic domain-array structures. To distinguish with the proposed C-CNN and show the intrinsic difference between real-valued and complex-valued based neural networks, we provide the whole structure of R-CNN in Supplementary Fig. 4, and the comparison between the real-valued and complex-valued based convolutional operation in Supplementary Fig. 3. As can be seen that while the volumetric shape of concentrated output looks similar for the real-valued convolutional operation, the ways by which they are calculated and interpreted are fundamentally different.

Figure 3a presents the results from a simple domain structure (15 domains with a regular grid position), and Fig. 3b shows the results from a more complex domain structure (50 domains with random overlapping position). When there exists significant phase wrapping, the R-CNN cannot recover the phase well due to the smoothing effect of real-valued convolution on the output phase. However, the jump in phase can be preserved because C-CNN produces real and imaginary outputs instead of amplitude and phase. To have a quantitative comparison, Fig. 3c, d presents the histograms of the structural similarity index measure (SSIM) for the predicted amplitude and phase as well as the \({\chi }^{2}\) error on the calculated diffraction patterns (see Supplementary Note 4 for the definition of the SSIM and \({\chi }^{2}\) error). Here, a total of 1000 test samples on simulated data with different domain structures are used to evaluate. As presented, the C-CNN outperforms the R-CNN in both simple and complex domain structures by achieving lower \({\chi }^{2}\) errors between ground truth and reconstructed diffraction patterns and higher SSIM for the predicted amplitude and phase with higher certainty. Supplementary Table 4 presents more numerical results showing that C-CNN consistently outperforms R-CNN in different domain structures.

Fig. 3: Representative results for the C-CNN and R-CNN for simulated test sets with different number of domains and domain structure.
figure 3

Predicted amplitude and phase in the real space with C-CNN and R-CNN for (a) 15 domains with grid position and (b) 50 domains with random position. Quantitative comparison on synthetic test set with histograms of SSIM calculated between prediction and the ground truth of amplitude and phase, and the χ2 errors between the input and reconstructed diffraction patterns with C-CNN and R-CNN for (c) 15 domains with grid position and (d) 50 domains with random position.

Full size image

We further investigate the robustness of the C-CNN model by adding Gaussian white noise to the original input diffraction patterns. The noise level is defined by the signal-to-noise ratio: \({{\rm{SNR}}}_{{\rm{dB}}}=10{\log }_{10}\left(\frac{{I}_{{\rm{s}}}}{{I}_{{\rm{n}}}}\right),\) where \({I}_{{\rm{s}}}\) and \({I}_{{\rm{n}}}\) refer to the power of the coherent diffraction intensity signal and noise, respectively. A higher SNR value means a lower strength of the noise. Figure 4 presents the predicted amplitude and phase of the real-space object with different noise levels introduced to the input diffraction. A sample from the test set is presented in Fig. 4 to illustrate the robustness of the Gaussian noise in the input. We find that the predicted phase from the C-CNN is more sensitive to the noise than the predicted amplitude. However, as the noise level increases, the model still provides excellent predictions. This indicates that the proposed C-CNN model is robust to a reasonable level of Gaussian noise. In addition, we plot the amplitude SSIM vs. SNR and phase SSIM vs. SNR curve in Supplementary Fig. 1 to clearly show the robustness of the C-CNN against the Gaussian noise, which illustrating that the resistance of C-CNN is about 5 dB for amplitude prediction and 8 dB for phase prediction. Finally, the performance of C-CNN on different amounts of scattered X-ray photons using simulate data is shown in Supplementary Fig. 9a, b indicating that C-CNN achieves comparable results with \({10}^{5}\) scattered photons and further lowering the number of scattered photons will degrade performance considerably.

Fig. 4: Resilience against Gaussian noise.
figure 4

a Input coherent diffraction patterns with different levels of Gaussian noise, from low noise level (i.e., 5 dB) to large noise (i.e., −1 dB). b Corresponding predicted amplitudes and (c) predicted phases.

Full size image

Performance on experimental XFEL data

In this section, the proposed C-CNN is applied to experimental XFEL data. The main issue with experimental data is the lack of ground truth for amplitude and phase in real space. To this end, we reconstruct the phase of the experimental XFEL data in an unsupervised learning manner. The unsupervised learning framework is illustrated in Fig. 2c. Specifically, we first estimate the amplitude and phase of the sample for the experimental XFEL diffraction data based on the pre-trained C-CNN model using synthetic data with a texture similar to the experimental data (see Supplementary Fig. 6 for the generation of the synthetic data). Then, we train another C-CNN model to refine those estimated phases and amplitudes with an unsupervised loss function using the estimated phase and amplitude as a starting point. Given the training set \(\{{{I}_{{\rm{i}}}^{{\rm{amp}}}\}}_{{\rm{i}}=1,\ldots ,n}\), where \({I}_{{\rm{i}}}^{{\rm{amp}}}\) is the amplitude of the input XFEL diffraction pattern, the unsupervised loss function is defined using the MAE between the measured diffraction and estimated diffraction:

$$L=\frac{1}{N}\mathop{\sum }\limits_{{\rm{i}}=1}^{N}\left||\right.F\left(\right.{g}_{\theta }\left({f}_{{\rm{\varphi }}}\left({\rm{\tau }}\left({I}_{{\rm{i}}}^{{\rm{amp}}}\right)\right)\right)\left|-{I}_{{\rm{i}}}^{{\rm{amp}}}\right|,$$
(2)

where \(F\left(\cdot \right)\) refers to the Fourier transform and \({\rm{\tau }}\left(\cdot \right)\) represents the function to convert the amplitude of the input diffraction pattern into its real and imaginary parts. \({f}_{{\rm{\varphi }}}\) denotes the C-CNN model pre-trained on the synthetic data with supervised loss defined in Eq. (1), and \({g}_{\theta }\) denotes the refined C-CNN model, which is updated with Eq. (2). Thus, during the unsupervised training process, we fixed the pre-trained model \({f}_{{\rm{\varphi }}}\) and only update the refined model \({g}_{\theta }\). Since the corresponding ground truth of the predicted phase and amplitude of a sample are not involved in the loss function, the above objective function, Eq. (2) is applicable to the experimental data directly.

The XFEL diffraction data originally contained 1002 pulse trains, each train containing 140 pulses. To remove the noise and obtain high quality diffraction images, we are pre-processing the raw data and finally obtain 20 images by averaging the high correlated images (see more details in Pre-processing experimental data section). We split 15 images for training and 5 images for testing.

Figure 5b demonstrates \({\chi }^{2}\) errors and the reconstructed diffraction patterns from two test experimental XFEL coherent X-ray diffraction samples after refined C-CNN model. Supplementary Fig. 5 illustrates that the reconstructed diffraction pattern shows significant improvement after refinement compared to before refinement, demonstrating its effectiveness. Figure 5c, d shows the corresponding predicted amplitude and phase in real space. The images are significantly distorted because they are presented in the inverse of the detector coordinates without attempting to transform to the sample coordinate system. Groups of domains are seen as clusters of bright spots, but each spot has a separate phase value as expected from Fig. 1b. The pixel size of the real-space images is 88 nm, so the domains size, estimated by peak width as marked in Fig. 1f should be 1–2 pixels wide which is observed in Fig. 5c. Thus, the prediction results in the real space are reasonable since it satisfies our assumptions and achieves lower \({\chi }^{2}\) errors. To further investigate the performance on different inputs, we present the \({\chi }^{2}\) errors histogram on the 1002 single-train experimental images in Supplementary Fig. 10. We find that 60% samples achieve \({\chi }^{2}\) around the 0.1 which is worse than average images since single-train images are noisy and have some outliers which will degrade the performance. Finally, we quantify the reproducibility of C-CNN by repeating five times with different seeds for training process and report the mean, standard deviation, maximum and minimum values of the predicted amplitude, phase correlation coefficient, and \({\chi }^{2}\) errors of the reconstructed diffraction pattern in Supplementary Table 3. The average correlation and standard deviation of \({\chi }^{2}\) errors on 5 trials shows that C-CNN could achieve good reproducibility for both amplitude prediction and reconstructed diffraction pattern. Model details are provided in Supplementary Note 6.

Fig. 5: Performance of the C-CNN model on the experimental XFEL coherent X-ray diffraction samples.
figure 5

a XFEL diffraction data used as input. b Calculated diffraction patterns with corresponding (c) Predicted amplitude, (d) Predicted phase in real space. Here, the corresponding \({\chi }^{2}\) errors between (a) and (b) are shown in (b).

Full size image

Moreover, we find the changes identified between the real-space images shown in Supplementary Fig. 8, and the red rectangle in the second column highlights the large value regions of the predicted amplitude, appear to be shifted with respect to each other suggesting a movement of the beam from image to image rather than internal sample fluctuations. An XFEL beam experiences SASE fluctuations38, which can result in changes of the optical wavefront of the X-ray beam as well as jittering the source position and beam pointing. The CRL optics used here are expected to produce an approximately Gaussian-shaped focus with no significant fringes39, but the wavefront distortions and jitter in position and pointing are likely to cause beam intensity modulations and small position changes in the position of the illuminated spot.

Discussion

In this study, we have developed a Complex-valued CNN for the phase retrieval problem. The C-CNN is shown to perform much better than R-CNN on synthetic data, especially under more complex conditions (i.e., large numbers of domains), and is robust against Gaussian noise. Furthermore, when we apply the C-CNN model to the experimental XFEL data invoking the pre-trained model as initialization, we find good agreement with the experimental data resulting in small \({\chi }^{2}\) errors. When applying the model to other similar experiments, one can use the trained C-CNN model to the obtained amplitude and phase in the real space directly. Otherwise, generating the corresponding simulated data for the experiments might be required. However, the rest of the training process for the refined C-CNN model is the same. As the C-CNN model can deal with large amounts of coherent diffraction patterns simultaneously, it will benefit experiments where large amounts of data are generated from the same experiments, for example, XFEL experiments. We expect a further improvement of the C-CNN model’s performance when a large and more diverse training dataset with known ground truth is applied for pretraining the model. It is difficult to compare the current model with the conventional method since the conventional method does not converge for our LSCO XFEL experimental data. We believe that the proposed C-CNN model will be critical to the coherent imaging technique, especially in the case that the conventional method fails. The demonstrated reconstruction method is general for all epitaxial thin-film systems and can be widely applied to coherent diffraction experiments using other sources (e.g., synchrotron), so long as they are stable over the exposure time40. In the future, we plan to further improve the performance of the C-CNN model on experimental XFEL data and incorporate some physical constraints into the framework.

Methods

Synthetic data generation

We generate synthetic data with random phase and elliptical domain size, motivated by the general appearance of Fig. 1f. The amplitude of domain \(G\left(m,n\right)\) is generated with the following equation:

$$G\left(m,n\right)={{\rm{e}}}^{\frac{{-\left[\left(m\,-\,\frac{{N}_{w}}{2}\right)\times \sin \theta\, +\left(m\,-\,\frac{{N}_{w}}{2}\right)\times \cos \theta\, \right]}^{2}}{{\sigma }_{x}^{2}}+\frac{{-\left[\left(n\,-\,\frac{{N}_{h}}{2}\right)\times \sin \theta\, -\left(n\,-\,\frac{{N}_{h}}{2}\right)\times \cos \theta\, \right]}^{2}}{{\sigma }_{y}^{2}}},$$
(3)

where \(m\in \left\{0,..,{N}_{w}\right\},n\in \left\{0,..,{N}_{h}\right\}\), \({N}_{w}\) and \({N}_{h}\) represent the width and height of the domain size, respectively. \(\theta\) denotes the rotation angle of domain. σx and σy are the semi-major width and semi-minor width of ellipse domain. The corresponding phase \(\varphi \left(m,n\right)\) is randomly selected within \(-{\rm{\pi }}\) to \({\rm{\pi }}\) with a uniform distribution. Thus, the small complex domain, with a size of \({N}_{w}\times {N}_{h}\), can be represented as G × ejφ. Then we piece such complex domain together to obtain a large \(64\times 64\) complex array with random phase. Finally, the diffraction pattern is obtained by calculating the Fourier transformation of the simulated complex data multiplied by a fixed elliptical shape Gaussian support representing the beam size. In addition, we can generate different numbers of domains by changing the \({\sigma }_{x}\), \({\sigma }_{y}\), \({N}_{w}\), and \({N}_{h}\) (i.e.,\({\sigma }_{x}=3,{\sigma }_{y}=6\), \({N}_{w}=17\), and \({N}_{h}=13\) for about 15 domains within the support shown in Fig. 3a). For the synthetic data, we fix \(\theta =29^\circ .\) The pre-trained model using for XFEL experimental data is trained on the synthetic data (\({\sigma }_{x}=1.5,{\sigma }_{y}=3\), \({N}_{w}=9\), \({N}_{h}=6\)) shown in Supplementary Fig. 6.

Pre-processing experimental data

The original raw XFEL diffraction data contained diffraction patterns from 1002 pulse trains, each train containing 140 pulses cropped to size of 128 × 102 pixels on the AGIPD. The raw XFEL images were noisy with only a few counts per pixel and appeared to be in a random order. To remove the noise and group the similar diffraction patterns, we first centered and cropped the raw images to 90 × 90 and then found the highly correlated patterns within each train by selecting those with the highest correlation coefficient and averaging them together to produce one single image per train. We then repeated the process for these 1002 average patterns and grouped them into highly correlated clusters for further averaging to obtain 20 final processed images. Supplementary Fig. 7 shows the correlation coefficient heatmap with raw XFEL experimental data and we group them in 20 clusters based on the dissimilarity matrix. We further center-cropped the average images into 64 × 64. We found that the diffraction patterns within each pulse train were generally better correlated than between trains.

ML model training

Our complex-valued neural network is trained with the Pytorch package. For the synthetic dataset, we generated 15,000 samples, 80% for training, 10% for validation, and 10% for testing. For the experimental diffraction data, we pre-processed the raw data and obtained a total of 20 images, and randomly split them into 15 diffraction patterns for training and 5 for testing. We optimize the model by using adaptive moment estimation (ADAM)41. The learning rate is initialized to 0.001, gradually decreasing by using the cosine annealing scheduler. The network was initialized with uniform Xavier42 and trained on a single NVIDIA V100 GPU for 500 epochs. The training took 3 h for the synthetic dataset and 30 min for the experimental data. For the synthetic dataset, we normalize the input amplitude between 0 and 1, and input phase between −π and π. For the experimental data, we first convert the input amplitude into the real/imaginary part by simply using the square root of input intensity. Then the obtained real and imaginary parts are normalized between 0 and 1 separately. To make the output phase between −π and π, we utilize the Leaky ReLU activation function to obtain the negative value for the real/imaginary parts. We saved the model at the end of training and selected the hyper-parameters (i.e., the size of the Gaussian support and learning rate) on the validation data and showed the results on the test set. More implementation details are reported in Supplementary Table 2.