Abstract
Motivated by the striking promise of quantum computation, Majorana bound states (MBSs) in solid-state systems have attracted wide attention in recent years. In particular, the wavefunction localisation of MBSs is a key feature and is crucial for their future implementation as qubits. Here we investigate the spatial and electronic characteristics of topological superconducting chains of iron atoms on the surface of Pb(110) by combining scanning tunnelling microscopy and atomic force microscopy. We demonstrate that the Fe chains are mono-atomic, structured in a linear manner and exhibit zero-bias conductance peaks at their ends, which we interpret as signature for a MBS. Spatially resolved conductance maps of the atomic chains reveal that the MBSs are well localised at the chain ends (≲25 nm), with two localisation lengths as predicted by theory. Our observation lends strong support to use MBSs in Fe chains as qubits for quantum-computing devices.
Similar content being viewed by others
Introduction
Majorana fermions are real solutions of the Dirac equation and, by definition, fermionic particles, which are their own antiparticles.1 Although intensely searched in particle physics as neutrinos, Majorana fermions have recently been predicted to occur as quasi-particle bound states in engineered solid-state systems.2 Such systems not only offer the possibility to observe the exotic properties of such Majorana bound states (MBSs) but also open up an interesting playground for topological quantum computing.2,3 The fundamental ingredients to generate MBSs in semiconductor–superconductor heterostructures is to combine a spin texture with an s-wave superconductor allowing to create a superconducting state with effective p-wave pairing, giving birth to a new state of matter—topological superconductivity.2,3 MBSs arise as zero-energy states lying in the superconducting gap and being spatially localised at the interfaces.
To generate spin textures, theoretical proposals have suggested to employ nanowires and magnetic chains with strong spin–orbit interaction4–9 or with self-tuning RKKY interactions.10–12 Until now, only few experimental works have reported successful observations of a zero-bias conductance peak (ZBP) via transport measurements in semiconductors interpreted as MBS signature,13–16 however, without addressing their spatial localisations in detail. Remarkably, Nadj-Perge et al.9 recently studied the spatial and spectral resolutions of the MBS in Fe chains on superconducting Pb by scanning tunnelling microscopy (STM) and reported the striking observation of a ZBP at the end of the atomic chains, as generically expected for MBSs.3 Experimentally, the induced proximity gap probed in the Fe chain is found to be very small (≈meV), whereas the exchange interaction is in the eV range, implying on theoretical grounds a large localisation length of the MBS wavefunction, in contrast to the observation9 that has triggered interesting discussions on the physical origin of the ZBP.17,18 It further implies that possible MBS in such chains may easily hybridise into conventional fermions, raising the question as to whether MBS in such Fe/Pb hybrid system will exhibit non-Abelian braiding statistics.3
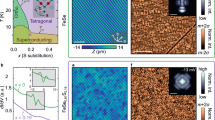
In this work, we go a decisive step further and combine STM and atomic force microscopy (AFM) measurements at low temperatures to characterise the electronic properties and structure, respectively, of superconducting Fe chains self-assembled on the surface of Pb(110) (Figure 1). To engineer such systems, atomically cleaned surfaces of an s-wave superconductor, Pb(110), were prepared by a few sputtering/annealing cycles (Supplementary Figure S1) on top of which Fe atoms were deposited on the sample kept at ≈400 K. In such a way, topographic STM images reveal the formation of long chains extending up to 70 nm (Figure 1b). In agreement with refs 9,19, chains are partially covered by small clusters mainly localised around their centres (Supplementary Figure S2), which is attributed to the clustering of Fe atoms. Careful real-space observations also reveal that numerous Pb vacancies are created in the vicinity of the chains. We assume that the relative high temperature required for the self-assembly might also promote the diffusion of Pb atoms and their nucleation at the chain sides. During our study, several chains having lengths from 40 to 70 nm (Figure 1b) were investigated and showed two distinct STM topographic signatures at their ends. The apparent ‘protrusion’ observed in Figure 1c corresponds to a variation of the STM height of ~10–15 pm compared with chains without such topographic feature (Figure 1d; Supplementary Figure S3). This STM height difference also observed in previous works9,19 appears to be too small (relative to other features) to correspond to a topographic peculiarity such as a cluster composed of few atoms, and might instead have a purely electronic origin associated with the ZBP. Nevertheless, it is worth mentioning that the MBS is stably pinned to zero-energy in the topological phase and, by definition, should not be influenced by structural details such as clusters at the chain end. Along the chains and independent of the termination types, no clear atomic periodicity has been observed by STM imaging (Supplementary Figure S3), which could unambiguously be related to the structure of the chain. We then systematically acquired conductance point-spectra at the two chain terminations to identify the presence of a ZBP generically interpreted as signatures for MBS. Figure 1e shows a typical single-point conductance spectrum at the end of the chain with a protusion (Figure 1c). The superconducting gaps measured with such tip are thus equal to Δ=1.1 meV being the superconducting gap of the lead probed with an STM tip in the metallic state. Similar conductance measurements were also taken on chain without protrusions such as Figure 1d but we did not observe a clear ZBP (Supplementary Figure S4). We thus particularly focus on those ‘protuded’ chains. We note that the lowest temperature of our experiments is 4.7 K, which limits our spectral resolution to about 1.4 meV with metallic STM tips (Supplementary Figure S1). Although the energy gap in our spectra is broadened compared with refs 9,19 due to the higher measurement temperature and the metallic nature of our STM tips, a superconducting proximity gap of ~1.1 meV is observed in the Fe chain as expected by the Bardeen-Cooper-Schrieffer (BCS) density of states (Supplementary Figure S1c,d). At zero-energy, a clear conductance peak is observed, which we interpret as a signature of a MBS that has been predicted to occur in such systems due to various mechanisms.7–12,19
Self-assembled Fe chains on Pb(110). (a) Model of the experiment: topological superconducting phase arises when mono-atomic iron chains with spin texture are grown on an s-wave superconductor (here Pb(110)). MBSs are then localised at the end of the chain and experimentally observed as ZBP in the conductance. (b) Topographic STM image of iron chains self-assembled on atomically clean Pb (110). (c,d) Topographic STM images of two chain terminations with a difference of apparent height (≈10 pm) at their ends, (Vt=−10 mV, It=100 pA). (e) dI/dV point-spectra obtained at the chain end in c showing a ZBP. The proximity gap equal to Δ=1.1 meV was measured with a metallic tip.
Results and Discussion
Electronic and structural characterisation along the mono-atomic Fe chain
A ZBP localised at the end of the chains is one of the hallmarks of a MBS.9 Alternatively, however, such a ZBP can arise from magnetic impurities such as Shiba (near) mid-gap states in the vicinity of single adatoms,20,21 molecules22,23 or disorder effects. To further identify the origin of the observed zero-energy subgap states and attribute it to a MBS, we compared STM and AFM imaging obtained at the atomic scale below and above the superconducting transition temperature, respectively (Figure 2).
Zero-bias electronic and structural characterisation of the Fe chain. (a) STM topographic image of the Fe chain end (Vt=−11 mV, It=80 pA, scale bar=5 nm). The inset shows the section characterised in the rest of the figure. (b) STM topography at Vt=10 mV and I=10 pA. (c) Constant-height zero-bias AFM image of the chain end acquired at 5 K. In contrast to STM topography, the AFM image clearly resolves the atomic structure of the Fe chain. Each protrusion corresponds to single Fe atoms aligned in a straight manner along the Pb(110) rows (Fe inter-atomic distance=0.37 nm). In c, site 1 shows the MBS and 2 the presence of slightly misaligned atoms along the chain. (d) Zero-bias normalised conductance maps ∝ LDOS acquired at 5 K. At site 1 where the MBS is localised, a zero-bias conductance peak is clearly observed at 5 K and vanishes at 10 K as a result of the suppression of the superconductivity. The LDOS obtained at 10 K shown in the inset is homogeneous along the chain, whereas weak oscillations are observed at 5 K due to the MBS wavefunction decay. (e) Comparison of LDOS profiles extracted along the chain at 5 (black dots) and 10 K (grey dots). The orange curve shows a tentative fit of the LDOS with the theoretical MBS wavefunction to extract the two localisation lengths.
Figure 2b shows a close-up STM topography of the investigated part of a long chain. The chain exhibits the topographic signature at its ends as well as a weak perturbation of the electronic density along the chain. This last feature might be caused by the presence of defects below or within the chain. However, as STM reflects the electronic density between tip and sample, the ‘true’ atomic structure can be masked by delocalised electronic states of the system.24,25 As we noticed for the present system, the STM topographic data can lead to important misinterpretations of the atomic structure determination of the chain (Supplementary Figure S3).
To unambiguously resolve the chain atomic structure, we employed the AFM imaging technique, which is rather insensitive to the delocalisation of electronic states close to the Fermi level. Figure 2c shows a constant-height zero-bias AFM image obtained at 5 K reflecting the true atomic structure of the chain. Each protrusion corresponds to a single Fe atom that is aligned and centred between the atomic rows of the Pb(110). The chains are mono-atomic and strictly ordered in a linear manner. The Fe inter-atomic distance is equal to 0.37 nm (see profile in Supplementary Figure S5), which is in good agreement with the atomic lattice along the Pb rows of ~0.35 nm. This suggests a high commensurability of the chain periodicity with the underlying substrate (the mismatch is ~0.6%) in contrast to the STM observation (Supplementary Figure S3).
The site marked by the arrow 1 in Figure 2c (X=2 nm) corresponds to the MBS location and shows a less negative Δf of about −2 Hz compared with the rest of the chain (Δf background=−20 Hz; see profile Supplementary Figure S5). This Δf variation is localised at the last two atoms of the chain and corresponds to a less attractive force regime between tip and sample. The AFM map (Figure 2c) shows a perfect round-shape halo of 0.8 nm in diameter as a spatial signature of this peculiarity. Within the halo, the last atoms are visible and perfectly aligned with the rest of the chain, thus excluding the absence of atomic disorder or corrugation effects. The decrease of the attractive forces at such close tip–sample distances implies additional contributions of repulsive forces between tip and sample. Tuning fork AFM is known to be sensitive to such forces that usually originate from Pauli exclusion principle between the electronic wavefunctions of the tip and surface.24 Given that two-end MBSs can host at most one fermion, it is plausible that a similar repulsive Pauli effect is responsible for the observed halo in the force maps at the MBS location. In comparison, site 2 shows a less pronounced Δf variation compared with that in site 1, which coincides with slightly misaligned Fe atoms with respect to the chain structure. The Δf is less negative by ≈−10 Hz compared with that of the chain. We further point out the absence of any halo at site 2 and conclude that the Δf variation is imputed to atomic disorders, most likely due to local topographic variations. We note that we also investigated chains without end-states and no such force contributions were observed (Supplementary Figure S4). This particular contribution in the force channel at the MBS location will be addressed in future works.
To further support our observation of MBS, we compared normalised conductance maps, i.e., (dI/dV)/(I/V) ∝ local density of state (LDOS) between the tip and sample at the Fermi level, obtained at the same locations and at ~5 K and 10 K, respectively. Figure 2d shows the LDOS (x, y) map at 5 K and reveals a clear ZBP, ascribed to the MBS, localised at the end of the chain as determined by the AFM data. A weak modulation of the LDOS is also observed along the chain that we attribute to the decay of the MBS wavefunction. At site 2, the LDOS is almost zero and might be due to weak magnetic perturbations induced by lattice disorder.20,22,23 To suppress the superconducting state of the system and thus to enforce the disappearance of the MBS, we measured the same chain above the critical temperature of lead (T⩾Tc=7.2 K). Although no clear changes of the STM topographies obtained at 10 K compared with those at 5 K were observed (Supplementary Figure S6), the corresponding normalised LDOS (x, y) map (see inset Figure 2d) shows a homogeneous LDOS along the chain, which drastically contrasts to the one at 5 K. By comparing the LDOS profiles taken along the chain at 5 K and 10 K (black and grey dots in Figure 2e, respectively), the ZBP has completely disappeared at 10 K (site 1) as well as the oscillations along the chain due to the suppression of topological superconductivity. As no external magnetic field is applied,9 we clearly address the interplay between superconductivity and the ZBP observed in our data, which provides a strong evidence of the MBS presence in this system.
The MBS localisation lengths
To further exclude other explanations of the ZBP,26 we next investigate another strong fingerprint of a MBS, namely, its wavefunction and associated localisation lengths.27 For this, we assume that the Fe chain with a proximity gap is driven into the topological phase by a spin texture that gives rise to a helical field (Figure 1a). Although Nadj-Perge et al.9 measured the chain magnetisation and concluded to a ferromagnetic behaviour, the precise value of the magnetisation is, however, not known and could be substantially away from full ferromagnetic order. In turn, this does not exclude helical order as the helix can be around the magnetisation axis with some small angle. Moreover, we wish to point out that, recently, such a helical state has been experimentally reported in a similar one-dimensional system.28 Such helical fields can either follow from spin–orbit interaction combined with Zeeman fields5,6,8 or exchange fields7,9 or from a ‘self-tuning’ RKKY interaction between the Fe spins.10–12 These two mechanisms are related by a spin-dependent gauge transformation and thus are mathematically equivalent.29 We further assume that the pitch of the helix is much larger than the lattice constant of the Fe chain, and that the helical field and the spin–orbit interaction are sufficiently strong. In this case, the MBS wavefunction is a superposition of contributions coming from different extrema in the spectrum, which results in two different localisation lengths for a single MBS.27 Assuming a semi-infinite chain with one MBS at each end (without overlap), these localisation lengths are determined by the corresponding gaps and given by
The MBS probability density is then defined as
where N is the normalisation constant, ξ1 and ξ2 are the localisation lengths, Δ and Δm are the proximity gap and the helical field gap of the chain (which depends on the exchange coupling constant), respectively, and kF is the Fermi wavevector of the chain. The topological phase of the chain is reached when Δm>Δ.10
The black curve shown in Figure 2e shows the LDOS profile extracted along the Fe chain at 5 K. The orange curve represents a tentative fit with the theoretical wavefunction giving ξ1≈110 nm and ξ2≈0.75 nm. We remark that ξ2, constituting the short localisation of the MBS, is about the same as the diameter of the halo observed by AFM in Figure 2c. However, the second localisation length ξ1 is only indicative as it exceeds the chain length. Indeed, the accurate estimation of ξ1 from the experimental data must be considered as valid when the Fe chains are exempted of structural peculiarities close to the MBS. In Figure 2d,e, the LDOS measurement along the chain is affected by the presence of the defect states along the chain (see 2 in Figure 2c) perturbing this fitting procedure.
To improve on such issues, we systematically investigated defect-free chains hosting MBS identified by both AFM and conductance measurements. Figure 3a,b shows the zero-bias constant-height AFM maps and the normalised LDOS (x, y) of such defect-free chains below Tc. Both data were acquired at slightly larger tip–sample separations (≈+50 pm) compared with Figure 2c. For that reason, the AFM image does not resolve the atomic lattice along the chain. However, both the dark halo (Figure 3a) and a ZBP in the conductance map (Figure 3b) remain present at the chain end testifying the MBS. As previously discussed, a non-negligible LDOS signal along the chain is detected in the LDOS map (Figure 3b) and decays with respect to the chain end. We extracted the period of the oscillations by performing a Fourier transformation of the conductance map (Supplementary Figure S7), which gives us the Fermi wavevector kF equal to 8.3 nm−1, i.e., a Fermi wavelength of 0.76 nm. The data were fitted with equation (2) by keeping the experimentally deduced parameters kF constant. Figure 3c shows the experimental LDOS(x) profile extracted along the chain (black dots). As shown by the superimposed blue curve, a remarkable agreement with the raw data periodicity is obtained allowing the extraction of the two localisation lengths ξ1 and ξ2. These localisation lengths are then found to be 22±5 and 0.75±0.14 nm, respectively, and correspond to ~59 and 2 atomic sites with respect to the chain lattice. Several data sets were analysed this way always showing the same values for these localisations (Supplementary Figure S8). In addition, the proximity gap associated with ξ2 is found to be Δm≈33 meV.
Majorana localisation lengths. (a) Constant-height zero-bias AFM image of the defect-free chain. (b) Zero-bias normalised LDOS of the chain hosting a MBS. (c) LDOS(X) profile (black dots) taken along the chain revealing the localisation lengths of the zero-bias conductance peak (x=0). The blue curve corresponds to the probability density of a Majorana Bound state with two localization lengths ξ1≈22 nm and ξ2≈0.72 nm. They correspond to 59 and 2 atomic sites, respectively. The orange curve approximates the wavefunction by considering the effect of the tip radius d=0.17 nm.
To account for the effect of the tip on the wavefunction measurement, we modify the formula for the probability density by including a broadening effect resulting from a tip size effect (see additional text in Supplementary Information). This approximation considers a symmetric apex having metallic character and giving the modulus squared of the wavefunctions at the Fermi energy. The orange curve of Figure 3b shows the result of such an approximation using a tip apex of 0.17 nm and demonstrates that such a broadening effect is sufficient to reasonably reconstruct the experimental data. We think that the use of lower measurement temperatures and p-wave STM tips30 in future experiments might help to resolve more precisely the MBSs wavefunction. In addition, more sophisticated models considering the chain on a two-dimensional or even three-dimensional lead substrate, into which the wavefunction of the MBS can leak (for a simple one-dimensional model, see section ‘Boundary effects’ in Supplementary Information), should give a better accuracy of the fit with the experimental data. Such more realistic models, however, are not available yet and are beyond the scope of the present work.
Conclusion
In conclusion, our results validate the existence of MBSs at the end of atomic iron chains on superconducting lead. Atomic scale AFM imaging shows that Fe adatoms form mono-atomic and straight chains on the Pb(110) surface, where ZBPs emerge at their extremities which we interpret as signature for MBS. These conductance peaks do not survive the suppression of superconductivity when increasing the sample temperature, in accordance with the expected behaviour of MBSs. Comparison between current and force channels further demonstrates that the AFM imaging is sensitive to the MBS observed as an additional force contribution. Furthermore, we spatially characterised the localisation of the MBS wavefunction that is composed of two localisation lengths extending up to ~60 atomic sites. This suggests that the relatively short localisation length of the MBS in such hybrid Fe/Pb systems arises from weak magnetic coupling of the chain atoms and might be tuned by weak external magnetic fields.10,27
Methods
Sample preparation
Single Pb(110) crystal was provided by Mateck GmbH. After an ex situ chemical treatment with hydrogen peroxide and acetic acid solution, the sample was atomically cleaned under ultrahigh vacuum by several cycles of sputtering and annealing. Iron atoms were deposited from a heated e-beam evaporator with a rate of ≈0.07 monolayer per min−1 on the surface and annealed at ≈400 K to promote the formation of chains.
Scanning probe microscopy
The scanning probe microscopy measurements were realised with a low-temperature STM/AFM microscope (Omicron Nanotechnology GmbH) based on a tuning fork sensor (f0≈25 kHz, k≈1,800 N m−1) and operated at ≈5 K in ultrahigh vacuum. All STM images were recorded in the constant current mode with the bias voltage applied to a bulk tungsten tip. The very-end of the tip apexes were prepared into a clean Cu(111) surface by gentle indentations. Conductance measurements were conducted at constant-height and zero-bias using the lock-in technique (f=570 Hz, A=200 μV) with the feedback loop opened at I=100 pA, V=10 mV. AFM images were performed in the constant-height mode at zero-bias with oscillation amplitudes of A=50 pm. The AFM images were obtained in the constant-height mode with a tuning fork sensor oscillating with amplitude of 50 pm. The variation of the resonance frequency, Δf, resulting from site-dependent interaction forces between tip and sample are dynamically tracked using a phase-lock loop while the probe travels over the surface.
References
Majorana, E. Teoria simmetrica dell’elettrone e del positrone. Nuovo Cimento 14, 171 (1937).
Alicea, J. New directions in the pursuit of majorana fermions in solid state systems. Rep. Prog. Phys. 75, 07501 (2012).
Kitaev, A. Y. Unpaired Majorana fermions in quantum wires. Phys.-Usp 44, 131 (2001).
Sato, M., Takahashi, Y. & Fujimoto, S. Non-Abelian topological orders and Majorana fermions in spin-singlet superconductors. Phys. Rev. B 82, 134521 (2010).
Oreg, Y., Refael, G. & V. Oppen, F. Helical liquids and Majorana bound states in quantum wires. Phys. Rev. Lett. 105, 177002 (2010).
Lutchyn, R. M., Sau, J. D. & Das Sarma, S. Majorana fermions and a topological phase transition in semiconductor-superconductor heterostructures. Phys. Rev. Lett. 105, 077001 (2010).
Nadj-Perge, S., Drozdov, I. K., Bernevig, B. A. & Yazdani, A. Proposal for realizing Majorana fermions in chains of magnetic atoms on a superconductor. Phys. Rev. B 88, 020407 (2013).
Pientka, F., Glazman, L. J. & v. Oppen, F. Topological superconducting phase in helical Shiba states. Phys. Rev. B 88, 155420 (2013).
Nadj-Perge, S. et al. Observation of Majorana fermions in ferromagnetic atomic chains on a superconductor. Science 346, 602 (2014).
Klinovaja, J., Stano, P., Yazdani, A. & Loss, D. Topological superconductivity and Majorana fermions in RKKY systems. Phys. Rev. Lett. 111, 186805 (2013).
Braunecker, B. & Simon, P. Interplay between classical magnetic moments and superconductivity in quantum one-dimensional conductors: toward a self-sustained topological Majorana phase. Phys. Rev. Lett. 111, 147202 (2013).
Vazifeh, M. & Franz, M. Self-organized topological state with Majorana fermions. Phys. Rev. Lett. 111, 206802 (2013).
Mourik, V. et al. Signatures of Majorana fermions in hybrid superconductor-semiconductor nanowire devices. Science 336, 1003 (2012).
Deng, M. T. et al. Anomalous zero-bias conductance peak in a Nb-InSb nanowire-Nb hybrid device. Nano Lett. 12, 6414 (2012).
Das, A. et al. Zero-bias peaks and splitting in an AlInAs nanowire topological superconductor as a signature of Majorana fermions. Nat. Phys. 8, 887 (2012).
Churchill, H. O. H. et al. Superconductor-nanowire devices from tunneling to the multichannel regime: Zero-bias oscillations and magnetoconductance crossover. Phys. Rev. B 87, 241401(R), (2013).
Dumitrescu, E., Roberts, B., Tewari, S., Sau, J. D. & Das Sarma, S. Majorana fermions in chiral topological ferromagnetic nanowires. Phys. Rev. B 91, 094505 (2015).
Peng, Y., Pientka, F., Glazman, L. I. & von Oppen, F. Strong localization of Majorana end states in chains of magnetic adatoms. Phys. Rev. Lett. 114, 106801 (2015).
Ruby, M. et al. End states and subgap structure in proximity-coupled chains of magnetic adatoms. Phys. Rev. Lett. 115, 197–204.
Yazdani, A., Jones, B. A., Lutz, C. P., Crommie, M. F. & Eigler, D. M. Probing the local effects of magnetic impurities on superconductivity. Science 275, 1767–1770 (1997).
Ji, S.-H. et al. Application of magnetic atom induced bound states in superconducting gap for chemical identification of single magnetic atoms. App. Phys. Lett. 96, 073113 (2010).
Franke, K. J., Schulze, G. & Pascual, J. I. Competition of superconducting phenomena and Kondo screening at the nanoscale. Science 332, 940–944 (2011).
Heinrich, B. W., Braun, L., Pascual, J. I. & Franke, K. J. Protection of excited spin states by a superconducting energy gap. Nat. Phys. 9, 765–768 (2013).
Gross, L., Mohn, F., Moll, N., Liljeroth, P. & Meyer, G. The chemical structure of a molecule resolved by atomic force microscopy. Science 325, 1110–1114 (2009).
Pawlak, R., Kawai, S., Fremy, S., Glatzel, T. & Meyer, E. Atomic-scale mechanical properties of orientated C60 revealed by noncontact atomic force microscopy. ACS Nano 54, 6349 (2011).
Ternes, M. et al. Subgap structure in asymmetric superconducting tunnel junctions. Phys. Rev. B 74, 132501 (2006).
Klinovaja, J. & Loss, D. Composite Majorana fermion wavefuntions in nanowires. Phys. Rev. B 86, 085408 (2012).
Menzel, M., Kubetzka, A., von Bergmann, Kristen & Wiesendanger, R. Parity effect in 120° spin spirals. Phys. Rev. Lett. 112, 047204 (2014).
Braunecker, B., Japaridze, G. I., Klinovaja, J. & Loss, D. Spin-selective Peierls transition in interacting one-dimensional conductors with spin-orbit interaction. Phys. Rev. B 82, 045127 (2010).
Gross, L. et al. High-resolution molecular orbital imaging using a p-wave STM Tip. Phys. Rev. Lett. 107, 086101 (2011).
Acknowledgements
This work was supported by the Swiss National Science Foundation, NCCR QSIT, Swiss Nanoscience Institute, Polish-Swiss Project PSPB-085/2010 and the EU Cost action MP1303.
Author information
Authors and Affiliations
Contributions
RP, DL and EM conceived and designed the research. RP, MK and TM prepared the samples. RP and MK performed the measurements. JK and DL provided theoretical support. RP, MK, EM, DL and JK analysed the data and wrote the manuscript with contributions from all authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no conflict of interest.
Additional information
Supplemental Information accompanies the paper on the npj Quantum Information website
Supplementary information
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Pawlak, R., Kisiel, M., Klinovaja, J. et al. Probing atomic structure and Majorana wavefunctions in mono-atomic Fe chains on superconducting Pb surface. npj Quantum Inf 2, 16035 (2016). https://doi.org/10.1038/npjqi.2016.35
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/npjqi.2016.35