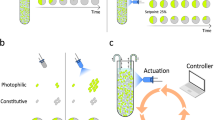
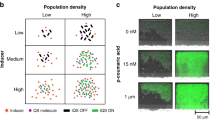
Abstract
Microbial ecologists are increasingly turning to small, synthesized ecosystems1–5 as a reductionist tool to probe the complexity of native microbiomes6,7. Concurrently, synthetic biologists have gone from single-cell gene circuits8–11 to controlling whole populations using intercellular signalling12–16. The intersection of these fields is giving rise to new approaches in waste recycling17, industrial fermentation18, bioremediation19 and human health16,20. These applications share a common challenge7 well-known in classical ecology21,22—stability of an ecosystem cannot arise without mechanisms that prohibit the faster-growing species from eliminating the slower. Here, we combine orthogonal quorum-sensing systems and a population control circuit with diverse self-limiting growth dynamics to engineer two ‘ortholysis’ circuits capable of maintaining a stable co-culture of metabolically competitive Salmonella typhimurium strains in microfluidic devices. Although no successful co-cultures are observed in a two-strain ecology without synthetic population control, the ‘ortholysis’ design dramatically increases the co-culture rate from 0% to approximately 80%. Agent-based and deterministic modelling reveal that our system can be adjusted to yield different dynamics, including phase-shifted, antiphase or synchronized oscillations, as well as stable steady-state population densities. The ‘ortholysis’ approach establishes a paradigm for constructing synthetic ecologies by developing stable communities of competitive microorganisms without the need for engineered co-dependency.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 digital issues and online access to articles
$119.00 per year
only $9.92 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Gravel, D. et al. Experimental niche evolution alters the strength of the diversity–productivity relationship. Nature 469, 89–92 (2011).
De Roy, K. et al. Environmental conditions and community evenness determine the outcome of biological invasion. Nat. Commun. 4, 1383 (2013).
Tanouchi, Y., Smith, R. P. & You, L. Engineering microbial systems to explore ecological and evolutionary dynamics. Curr. Opin. Biotechnol. 23, 791–797 (2012).
Wintermute, E. H. & Silver, P. A. Emergent cooperation in microbial metabolism. Mol. Syst. Biol. 6, 407 (2010).
Klitgord, N. & Segre, D. Environments that induce synthetic microbial ecosystems. PLoS Comput. Biol. 6, e1001002 (2010).
Little, A. E., Robinson, C. J., Peterson, S. B. & Raffa, K. F. in The Social Biology of Microbial Communities: Workshop Summary (ed. Mack, A. ) Vol. 62, 375–401 (National Academies, 2012).
De Roy, K., Marzorati, M., Van den Abbeele, P., Van de Wiele, T. & Boon, N. Synthetic microbial ecosystems: an exciting tool to understand and apply microbial communities. Environ. Microbiol. 16, 1472–1481 (2014).
Gardner, T. S., Cantor, C. R. & Collins, J. J. Construction of a genetic toggle switch in Escherichia coli. Nature 403, 339–342 (2000).
Elowitz, M. B. & Leibler, S. A synthetic oscillatory network of transcriptional regulators. Nature 403, 335–338 (2000).
Hasty, J., McMillen, D. & Collins, J. J. Engineered gene circuits. Nature 420, 224–230 (2002).
Endy, D. Foundations for engineering biology. Nature 438, 449–453 (2005).
You, L., Cox, R. S., Weiss, R. & Arnold, F. H. Programmed population control by cell–cell communication and regulated killing. Nature 428, 868–871 (2004).
Brenner, K., Karig, D. K., Weiss, R. & Arnold, F. H. Engineered bidirectional communication mediates a consensus in a microbial biofilm consortium. Proc. Natl Acad. Sci. USA 104, 17300–17304 (2007).
Danino, T., Mondragón-Palomino, O., Tsimring, L. & Hasty, J. A synchronized quorum of genetic clocks. Nature 463, 326–330 (2010).
Chen, Y., Kim, J. K., Hirning, A. J., Josic, K. & Bennett, M. R. Emergent genetic oscillations in a synthetic microbial consortium. Science 349, 986–989 (2015).
Din, M. O. et al. Synchronized cycles of bacterial lysis for in vivo delivery. Nature 536, 81–85 (2016).
Fulget, N., Poughon, L., Richalet, J. & Lasseur, C. Melissa: global control strategy of the artificial ecosystem by using first principles models of the compartments. Adv. Space Res. 24, 397–405 (1999).
Chen, Y. Development and application of co-culture for ethanol production by co-fermentation of glucose and xylose: a systematic review. J. Ind. Microbiol. Biotechnol. 38, 581–597 (2011).
Dejonghe, W. et al. Synergistic degradation of linuron by a bacterial consortium and isolation of a single linuron-degrading variovorax strain. Appl. Environ. Microbiol. 69, 1532–1541 (2003).
Petrof, E. O. et al. Stool substitute transplant therapy for the eradication of Clostridium difficile infection: ‘repoopulating’ the gut. Microbiome 1, 3 (2013).
Gause, G. F. The Struggle for Existence (Courier Corporation, 2003).
Faust, K. & Raes, J. Microbial interactions: from networks to models. Nat. Rev. Microbiol. 10, 538–550 (2012).
Scott, S. R. & Hasty, J. Quorum sensing communication modules for microbial consortia. ACS Synth. Biol. 5, 969–977 (2016).
Renda, B. A., Hammerling, M. J. & Barrick, J. E. Engineering reduced evolutionary potential for synthetic biology. Mol. Biosyst. 10, 1668–1678 (2014).
Danino, T. et al. Programmable probiotics for detection of cancer in urine. Sci. Transl. Med. 7, 289ra84 (2015).
Bittihn, P., Hasty, J. & Tsimring, L. S. Suppression of beneficial mutations in dynamic microbial populations. Phys. Rev. Lett. 118, 028102 (2017).
Balagaddé, F. K. et al. A synthetic Escherichia coli predator–prey ecosystem. Mol. Syst. Biol. 4, 187 (2008).
Shou, W., Ram, S. & Vilar, J. M. Synthetic cooperation in engineered yeast populations. Proc. Natl Acad. Sci. USA 104, 1877–1882 (2007).
Foster, K. R. & Bell, T. Competition, not cooperation, dominates interactions among culturable microbial species. Curr. Biol. 22, 1845–1850 (2012).
Zemke, A. C. & Bomberger, J. M. Microbiology: social suicide for a good cause. Curr. Biol. 26, R80–R82 (2016).
Quan, J. & Tian, J. Circular polymerase extension cloning of complex gene libraries and pathways. PLoS ONE 4, e6441 (2009).
Prindle, A. et al. A sensing array of radically coupled genetic ‘biopixels’. Nature 481, 39–44 (2012).
Pédelacq, J.-D., Cabantous, S., Tran, T., Terwilliger, T. C. & Waldo, G. S. Engineering and characterization of a superfolder green fluorescent protein. Nat. Biotechnol. 24, 79–88 (2006).
Lutz, R. & Bujard, H. Independent and tight regulation of transcriptional units in Escherichia coli via the lacr/o, the tetr/o and arac/i1-i2 regulatory elements. Nucleic Acids Res. 25, 1203–1210 (1997).
Marguet, P., Tanouchi, Y., Spitz, E., Smith, C. & You, L. Oscillations by minimal bacterial suicide circuits reveal hidden facets of host-circuit physiology. PLoS ONE 5, e11909 (2010).
Volfson, D., Cookson, S., Hasty, J. & Tsimring, L. S. Biomechanical ordering of dense cell populations. Proc. Natl Acad. Sci. USA 105, 15346–15351 (2008).
Mather, W., Mondragón-Palomino, O., Danino, T., Hasty, J. & Tsimring, L. S. Streaming instability in growing cell populations. Phys. Rev. Lett. 104, 208101 (2010).
Acknowledgements
This material is based on work supported by NIH/NIGMS grant no. RO1-GM069811 and by the San Diego Center for Systems Biology under NIH/NIGMS grant no. P50-GM085764. S.R.S. was partially funded by the National Science Foundation Graduate Research Fellowship under grant no. DGE-1144086. P.B. acknowledges support from HFSP fellowship LT000840/2014-C. L.X. and L.S.T. were partially supported by ONR grant no. N00014-16-1-2093. Any opinion, findings and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the funding agencies.
Author information
Authors and Affiliations
Contributions
All authors contributed extensively to the work presented in this paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary information
Supplementary Figures 1–5; Supplementary Table 1 (PDF 1447 kb)
Supplementary Video 1
This video shows timelapse fluorescence microscopy of the SLC in strain 2 (ssrA tag on LuxI) at 20x magnification. Images were taken every 2 min of a 100 × 100 μm chamber. Timestamp is in minutes. (AVI 22816 kb)
Supplementary Video 2
This video shows timelapse fluorescence microscopy of the SLC in strain 1 (no ssrA tag on LuxI) at 20x magnification. Images were taken every 2 min of a 100 × 100 μm chamber. Timestamp is in minutes. (AVI 22966 kb)
Supplementary Video 3
Video of non-lysis co-culture on a microfluidic device at 20x magnification. Strain 4 (non-lysis Lux-CFP) and strain 6 (non-lysis Rpa-GFP). Timelapse fluorescence microscopy images were taken every 3 min. Timestamp is in minutes. (AVI 28306 kb)
Supplementary Video 4
Video of dual lysis co-culture on a microfluidic device at 20x magnification. Strain 5 (lysis Lux-CFP) and Strain 7 (lysis Rpa-GFP). Timelapse fluorescence microscopy images were taken every 3 min. Timestamp is in minutes. (AVI 27373 kb)
Supplementary Video 5
Timelapse agent-based simulation of two lysis strains both in the oscillatory regime. (AVI 4083 kb)
Supplementary Video 6
Timelapse agent-based simulation of two lysis strains: one in the oscillatory regime and the other in the constant lysis regime. (AVI 5447 kb)
Rights and permissions
About this article
Cite this article
Scott, S., Din, M., Bittihn, P. et al. A stabilized microbial ecosystem of self-limiting bacteria using synthetic quorum-regulated lysis. Nat Microbiol 2, 17083 (2017). https://doi.org/10.1038/nmicrobiol.2017.83
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/nmicrobiol.2017.83
This article is cited by
-
Engineered autonomous dynamic regulation of metabolic flux
Nature Reviews Bioengineering (2023)
-
Biotechnological methods to remove microplastics: a review
Environmental Chemistry Letters (2023)
-
The Application Potential of Synthetic Biology in Microbial Communication
Current Clinical Microbiology Reports (2023)
-
Feedforward growth rate control mitigates gene activation burden
Nature Communications (2022)
-
Design of stable and self-regulated microbial consortia for chemical synthesis
Nature Communications (2022)