Abstract
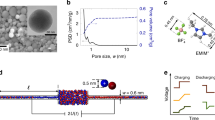
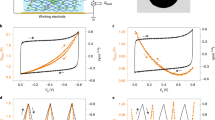
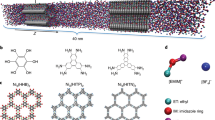
Ionic transport inside porous carbon electrodes underpins the storage of energy in supercapacitors and the rate at which they can charge and discharge, yet few studies have elucidated the materials properties that influence ion dynamics. Here we use in situ pulsed field gradient NMR spectroscopy to measure ionic diffusion in supercapacitors directly. We find that confinement in the nanoporous electrode structures decreases the effective self-diffusion coefficients of ions by over two orders of magnitude compared with neat electrolyte, and in-pore diffusion is modulated by changes in ion populations at the electrode/electrolyte interface during charging. Electrolyte concentration and carbon pore size distributions also affect in-pore diffusion and the movement of ions in and out of the nanopores. In light of our findings we propose that controlling the charging mechanism may allow the tuning of the energy and power performances of supercapacitors for a range of different applications.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 digital issues and online access to articles
$119.00 per year
only $9.92 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
References
Chmiola, J. et al. Anomalous increase in carbon capacitance at pore sizes less than 1 nanometer. Science 313, 1760–1763 (2006).
Raymundo-Piñero, E., Kierzek, K., Machnikowski, J. & Béguin, F. Relationship between the nanoporous texture of activated carbons and their capacitance properties in different electrolytes. Carbon 44, 2498–2507 (2006).
Balducci, A. Electrolytes for high voltage electrochemical double layer capacitors: a perspective article. J. Power Sources 326, 534–540 (2016).
Zhong, C. et al. A review of electrolyte materials and compositions for electrochemical supercapacitors. Chem. Soc. Rev. 44, 7484–7539 (2015).
Griffin, J. M. et al. In situ NMR and electrochemical quartz crystal microbalance reveal the structure of the electric double-layer in supercapacitor electrodes. Nat. Mater. 14, 812–819 (2015).
Forse, A. C. et al. NMR study of ion dynamics and charge storage in ionic liquid supercapacitors. J. Am. Chem. Soc. 137, 7231–7242 (2015).
Griffin, J. M. et al. Ion counting in supercapacitor electrodes using NMR spectroscopy. Faraday Disc. 176, 49–68 (2014).
Luo, Z.-X. et al. Dehydration of ions in voltage-gated carbon nanopores observed by in situ NMR. J. Phys. Chem. Lett. 6, 5022–5026 (2015).
Deschamps, M. et al. Exploring electrolyte organization in supercapacitor electrodes with solid-state NMR. Nat. Mater. 12, 351–358 (2013).
Tsai, W.-Y., Taberna, P.-L. & Simon, P. Electrochemical quartz crystal microbalance (EQCM) study of ion dynamics in nanoporous carbons. J. Am. Chem. Soc. 136, 8722–8728 (2014).
Levi, M. D., Salitra, G., Levy, N., Aurbach, D. & Maier, J. Application of a quartz-crystal microbalance to measure ionic fluxes in microporous carbons for energy storage. Nat. Mater. 8, 872–875 (2009).
Prehal, C. et al. Tracking the structural arrangement of ions in carbon supercapacitor nanopores using in-situ small-angle X-ray scattering. Energy Environ. Sci. 8, 1725–1735 (2015).
Richey, F. W., Tran, C., Kalra, V. & Elabd, Y. A. Ionic liquid dynamics in nanoporous carbon nanofibers in supercapacitors measured with in operando infrared spectroelectrochemistry. J. Phys. Chem. C 118, 21846–21855 (2014).
Boukhalfa, S. et al. In-situ small angle neutron scattering revealing ion sorption in microporous carbon electrical double layer capacitors. ACS Nano 8, 2495–2503 (2014).
Merlet, C. et al. On the molecular origin of supercapacitance in nanoporous carbon electrodes. Nat. Mater. 11, 306–310 (2012).
Kondrat, S., Wu, P., Qiao, R. & Kornyshev, A. A. Accelerating charging dynamics in subnanometre pores. Nat. Mater. 13, 387–393 (2014).
Fedorov, M. V. & Kornyshev, A. A. Ionic liquids at electrified interfaces. Chem. Rev. 114, 2978–3036 (2014).
He, Y. et al. Importance of ion packing on the dynamics of ionic liquids during micropore charging. J. Phys. Chem. Lett. 7, 36–42 (2016).
Forse, A. C. et al. Nuclear magnetic resonance study of ion adsorption on microporous carbide-derived carbon. Phys. Chem. Chem. Phys. 15, 7722–7730 (2013).
Borchardt, L., Oschatz, M., Paasch, S., Kaskel, S. & Brunner, E. Interaction of electrolyte molecules with carbon materials of well-defined porosity: characterization by solid-state NMR spectroscopy. Phys. Chem. Chem. Phys. 15, 15177–15184 (2013).
Forse, A. C., Merlet, C. M., Griffin, J. M. & Grey, C. P. New perspectives on the charging mechanisms of supercapacitors. J. Am. Chem. Soc. 138, 5731–5744 (2016).
Salanne, M. et al. Efficient storage mechanisms for building better supercapacitors. Nat. Energy 1, 16070 (2016).
Pean, C. et al. Confinement, desolvation, and electrosorption effects on the diffusion of ions in nanoporous carbon electrodes. J. Am. Chem. Soc. 137, 12627–12632 (2015).
Kondrat, S. & Kornyshev, A. A. Pressing a spring: What does it take to maximize the energy storage in nanoporous supercapacitors? Nanoscale Horiz. 1, 45–52 (2016).
Wang, H. et al. In situ NMR spectroscopy of supercapacitors: insight into the charge storage mechanism. J. Am. Chem. Soc. 135, 18968–18980 (2013).
Forse, A. C., Griffin, J. M., Presser, V., Gogotsi, Y. & Grey, C. P. Ring current effects: factors affecting the NMR chemical shift of molecules adsorbed on porous carbons. J. Phys. Chem. C 118, 7508–7514 (2014).
Merlet, C., Forse, A. C., Griffin, J. M., Frenkel, D. & Grey, C. P. Lattice simulation method to model diffusion and NMR spectra in porous materials. J. Chem. Phys. 142, 094701 (2015).
Callaghan, P. T. Translational Dynamics and Magnetic Resonance (Oxford Univ. Press, 2011).
Karger, J., Ruthven, D. M. & Theodorou, D. N. Diffusion in Nanoporous Materials (Wiley, 2012).
Dubinin, M. M., Vartapetian, R. S., Voloshchuk, A. M., Karger, J. & Pfeifer, H. NMR study of translational mobility of molecules adsorbed on active carbons. Carbon 26, 515–520 (1988).
Kalugin, O. N., Chaban, V. V., Loskutov, V. V. & Prezhdo, O. V. Uniform diffusion of acetonitrile inside carbon nanotubes favors supercapacitor performance. Nano Lett. 8, 2126–2130 (2008).
Oschatz, M. et al. Nanostructure characterization of carbide-derived carbons by morphological analysis of transmission electron microscopy images combined with physisorption and Raman spectroscopy. Carbon 105, 314–322 (2016).
Forse, A. C. et al. New insights into the structure of nanoporous carbons from NMR, Raman, and pair distribution function analysis. Chem. Mater. 27, 6848–6857 (2015).
Harris, P. J. F. Fullerene-like models for microporous carbon. J. Mater. Sci. 48, 565–577 (2013).
Alam, T. M. & Osborn Popp, T. M. In-pore exchange and diffusion of carbonate solvent mixtures in nanoporous carbon. Chem. Phys. Lett. 658, 51–57 (2016).
Stallmach, F. et al. NMR studies on the diffusion of hydrocarbons on the metal-organic framework material MOF-5. Angew. Chem. Int. Ed. Engl. 45, 2123–2126 (2006).
Noda, A., Hayamizu, K. & Watanabe, M. Pulsed-gradient spin-echo 1H and 19F NMR ionic diffusion coefficient, viscosity, and ionic conductivity of non-chloroaluminate room-temperature ionic liquids. J. Phys. Chem. B 105, 4603–4610 (2001).
Every, H. A., Bishop, A. G., Macfarlane, D. R., Ora, G. & Forsyth, M. Transport properties in a family of dialkylimidazolium ionic liquids. Phys. Chem. Chem. Phys. 6, 1758–1765 (2004).
Hou, J., Zhang, Z. & Madsen, L. A. Cation/anion associations in ionic liquids modulated by hydration and ionic medium. J. Phys. Chem. B 115, 4576–4582 (2011).
Burt, R. et al. Capacitance of nanoporous carbon-based supercapacitors is a trade-off between the concentration and the separability of the ions. J. Phys. Chem. Lett. 7, 4015–4021 (2016).
Kondrat, S. & Kornyshev, A. Charging dynamics and optimization of nanoporous supercapacitors. J. Phys. Chem. C 117, 12399–12406 (2013).
Korenblit, Y. et al. High-rate electrochemical capacitors based on ordered mesoporous silicon carbide-derived carbon. ACS Nano 4, 1337–1344 (2010).
Péan, C. et al. On the dynamics of charging in nanoporous carbon-based supercapacitors. ACS Nano 8, 1576–1583 (2014).
Redondo, E., Carretero-González, J., Goikolea, E., Ségalini, J. & Mysyk, R. Effect of pore texture on performance of activated carbon supercapacitor electrodes derived from olive pits. Electrochim. Acta 160, 178–184 (2015).
Itoi, H., Nishihara, H., Kogure, T. & Kyotani, T. Three-dimensionally arrayed and mutually connected 1.2-nm nanopores for high-performance electric double layer capacitor. J. Am. Chem. Soc. 20, 1165–1167 (2011).
Krachkovskiy, S. A. et al. Visualization of steady-state ionic concentration profiles formed in electrolytes during Li-ion battery operation and determination of mass-transport properties by in situ magnetic resonance imaging. J. Am. Chem. Soc. 138, 7992–7999 (2016).
Ray, P. et al. Insights into bulk electrolyte effects on the operative voltage of electrochemical double-layer capacitors. J. Phys. Chem. C 120, 12325–12336 (2016).
Sigalov, S. et al. Selective adsorption of multivalent ions into TiC-derived nanoporous carbon. Carbon 50, 3957–3960 (2012).
Schütter, C. et al. Rational design of new electrolyte materials for electrochemical double layer capacitors. J. Power Sources 326, 541–548 (2016).
Hayamizu, K. et al. Studies on the translational and rotational motions of ionic liquids composed of N-methyl-N-propyl-pyrrolidinium (P13) cation and bis(trifluoromethanesulfonyl)amide and bis(fluorosulfonyl)amide anions and their binary systems including lithium salts. J. Chem. Phys. 133, 194505 (2010).
Zhang, Z. & Madsen, L. A. Observation of separate cation and anion electrophoretic mobilities in pure ionic liquids. J. Chem. Phys. 140, 084204 (2014).
Gouverneur, M., Kopp, J., Wüllen, L. & Van Schönhoff, M. Direct determination of ionic transference numbers in ionic liquids by electrophoretic NMR. Phys. Chem. Chem. Phys. 17, 30680–30686 (2015).
Neimark, A. V., Lin, Y., Ravikovitch, P. I. & Thommes, M. Quenched solid density functional theory and pore size analysis of micro-mesoporous carbons. Carbon 47, 1617–1628 (2009).
Cotts, R. M., Hoch, M. J. R., Sun, T. & Markert, J. T. Pulsed field gradient stimulated echo methods for improved NMR diffusion measurements in heterogeneous systems. J. Magn. Reson. 266, 252–266 (1989).
Forse, A. C. et al. Research data set supporting ‘Direct observation of ion dynamics in supercapacitor electrodes using in situ diffusion NMR spectroscopy’. Cambridge Research Repository, Apollohttp://dx.doi.org/10.17863/CAM.7075 (2017).
Acknowledgements
The authors acknowledge the EPSRC (through the Supergen consortium for A.C.F., J.M.G. and J.C.-G.), the School of the Physical Sciences of the University of Cambridge (via an Oppenheimer Research Fellowship, C.M.), the EU Graphene Flagship (A.-R.O.R.), and the EU ERC (through an Advanced Fellowship to C.P.G.) for financial support. This work was also supported as part of the NorthEast Center for Chemical Energy Storage (NECCES), an Energy Frontier Research Center funded by the US Department of Energy (DOE), Office of Science, Basic Energy Sciences, under Award no. DE-SC0012583 (N.M.T.). We thank P. Bayley for assistance with PFG NMR experiments and the engineering of in situ apparatus, and A. Sederman for assistance with initial PFG NMR experiments.
Author information
Authors and Affiliations
Contributions
A.C.F. prepared supercapacitor cells, performed PFG NMR experiments and analysed the data. J.M.G. recorded and analysed NMR experiments to determine total in-pore ion populations. N.M.T. performed initial PFG NMR experiments. A.-R.O.R. recorded scanning electron micrographs and gas sorption isotherms. All authors contributed to design of the research, the discussion of the data and the writing of the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures 1–9, Supplementary Table 1, Supplementary Discussion, Supplementary References (PDF 1460 kb)
Rights and permissions
About this article
Cite this article
Forse, A., Griffin, J., Merlet, C. et al. Direct observation of ion dynamics in supercapacitor electrodes using in situ diffusion NMR spectroscopy. Nat Energy 2, 16216 (2017). https://doi.org/10.1038/nenergy.2016.216
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/nenergy.2016.216
This article is cited by
-
An ordered, self-assembled nanocomposite with efficient electronic and ionic transport
Nature Materials (2023)
-
Operando NMR electrochemical gating studies of ion dynamics in PEDOT:PSS
Nature Materials (2023)
-
Developing in situ electron paramagnetic resonance characterization for understanding electron transfer of rechargeable batteries
Nano Research (2023)
-
Continuous transition from double-layer to Faradaic charge storage in confined electrolytes
Nature Energy (2022)
-
Artificial channels for confined mass transport at the sub-nanometre scale
Nature Reviews Materials (2021)