Abstract
The study of photoexcited strongly correlated materials is attracting growing interest since their rich phase diagram often translates into an equally rich out-of-equilibrium behaviour. With femtosecond optical pulses, electronic and lattice degrees of freedom can be transiently decoupled, giving the opportunity of stabilizing new states inaccessible by quasi-adiabatic pathways. Here we show that the prototype Mott–Hubbard material V2O3 presents a transient non-thermal phase developing immediately after ultrafast photoexcitation and lasting few picoseconds. For both the insulating and the metallic phase, the formation of the transient configuration is triggered by the excitation of electrons into the bonding a1g orbital, and is then stabilized by a lattice distortion characterized by a hardening of the A1g coherent phonon, in stark contrast with the softening observed upon heating. Our results show the importance of selective electron–lattice interplay for the ultrafast control of material parameters, and are relevant for the optical manipulation of strongly correlated systems.
Similar content being viewed by others
Introduction
The Mott metal-to-insulator transition (MIT)1 is the perfect example of how thermodynamic parameters can affect the electronic structure of a material and its conducting properties. At equilibrium, temperature, doping and pressure act as driving forces for such transitions2, that invariably involve also a lattice modification—either with a change of symmetry, like for instance in VO2 (ref. 3) or with a lattice parameter jump like in V2O3 (ref. 4). It is actually often unclear whether the lattice or the electronic structure is the trigger for the MIT since at equilibrium both change together. This question can be answered by driving one far from equilibrium and observing the reaction of the other. Thus, time-resolved pump–probe techniques5,6,7,8,9,10,11 can provide this answer, as long as the response of the electrons and of the lattice can be separately analysed.
We adopted a combined experimental and theoretical approach to study the ultrafast evolution of the Mott–Hubbard prototype (V1−xCrx)2O3 (ref. 12). The phase diagram of V2O3 contains three phases: a paramagnetic metallic (PM) phase, a paramagnetic insulating (PI) phase and an antiferromagnetic insulator phase. The isostructural Mott transition is between the PI and the PM phases13. This archetypal material gives the opportunity of comparatively observing the ultrafast evolution of a Mott system starting both from the insulating and the metallic phase, whereas previous studies have generally focused only on the Mott insulator as ground state5,6,8,9,10 or, for other systems, on the interplay between spin density wave states14 and coherent optical lattice oscillations15. In all our experiments, the energy of the pump pulses (1.55 eV) corresponds to the transition from  to a1g orbitals. Thus, optical pumping directly increases the a1g population while decreasing the
to a1g orbitals. Thus, optical pumping directly increases the a1g population while decreasing the  one. Using time-resolved photoelectron spectroscopy (trPES) we directly probe the electronic structure, while time-resolved X-ray diffraction (trXRD) and time-resolved reflectivity (TRR) give access to the lattice evolution16,17,18,19.
one. Using time-resolved photoelectron spectroscopy (trPES) we directly probe the electronic structure, while time-resolved X-ray diffraction (trXRD) and time-resolved reflectivity (TRR) give access to the lattice evolution16,17,18,19.
Here we show that with this multitechnique approach one can unambiguously disentangle the contribution of electrons and lattice to the non-equilibrium dynamics of the system, and we find that in the PI phase the gap is instantaneously filled and a non-thermal transient state that lasts 2 ps is created. In the PM phase, the quasiparticle (QP) signal shows an immediate appreciable spectral redistribution across EF, which also lasts 2 ps, once again not compatible with thermal heating. In both phases we find that the lattice conspires to stabilize the non-thermal transient electronic state. Ab initio density functional theory with generalized gradient approximations (DFT-GGA) results supplemented by simple Hartree–Fock (HF) calculations suggest that the gap filling is driven by the non-equilibrium population imbalance between the  and a1g orbitals, which effectively weakens the correlation strength.
and a1g orbitals, which effectively weakens the correlation strength.
Results
Time-resolved photoelectron spectroscopy
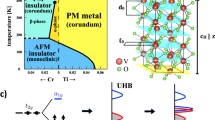
In vanadium sesquioxide the octahedral crystal field leads to the d-orbital splitting into a lower t2g and an upper  . Since the octahedron has a trigonal distortion, the t2g are split into a lower twofold degenerate
. Since the octahedron has a trigonal distortion, the t2g are split into a lower twofold degenerate  orbital and an upper non-degenerate a1g (Fig. 1). The hybridization between the two nearest vanadium atoms, which are lined up along the c axis, causes a large splitting between bonding a1g(σ) and antibonding a1g(σ*) states. In spite of that, the a1g orbital remains mostly unoccupied in the PI phase, whereas the
orbital and an upper non-degenerate a1g (Fig. 1). The hybridization between the two nearest vanadium atoms, which are lined up along the c axis, causes a large splitting between bonding a1g(σ) and antibonding a1g(σ*) states. In spite of that, the a1g orbital remains mostly unoccupied in the PI phase, whereas the  orbitals are occupied by almost one electron each20,21. V2O3 PI can thus be viewed as a half-filled two-band Mott insulator stabilized by the correlation-enhanced trigonal field that pushes above the Fermi energy (EF) the a1g orbitals21,22, whose occupancy indeed jumps across the doping- or temperature-driven Mott transition23 causing the opening of a gap24,25, while is smoother across the pressure-driven one13,26. The nature and indicative energy position of the relevant orbitals for each phase can be found in Fig. 2c,f, where we show the calculated density of states (DOS) from ref. 22. This inequivalent behaviour in temperature versus pressure of the MIT, and the related deep intertwining between strong correlations and lattice structure suggest that a major issue in time-resolved experiments is to distinguish a temperature increase from a transient non-thermal phase, such as hidden phases27,28.
orbitals are occupied by almost one electron each20,21. V2O3 PI can thus be viewed as a half-filled two-band Mott insulator stabilized by the correlation-enhanced trigonal field that pushes above the Fermi energy (EF) the a1g orbitals21,22, whose occupancy indeed jumps across the doping- or temperature-driven Mott transition23 causing the opening of a gap24,25, while is smoother across the pressure-driven one13,26. The nature and indicative energy position of the relevant orbitals for each phase can be found in Fig. 2c,f, where we show the calculated density of states (DOS) from ref. 22. This inequivalent behaviour in temperature versus pressure of the MIT, and the related deep intertwining between strong correlations and lattice structure suggest that a major issue in time-resolved experiments is to distinguish a temperature increase from a transient non-thermal phase, such as hidden phases27,28.
(a) (V1−xMx)2O3 phase diagram; the cross and the plus symbols indicate the experimental data points. (b) Temperature dependence of the equilibrium photoemission spectra for (V1−xCrx)2O3 (x=0.028 PI phase, x=0 PM phase). Temperature differences are shown for each doping, which are used as a thermal equilibrium reference in comparison with the photoexcited spectra. Upon increasing the temperature, the spectral weight is transferred into the Mott gap in the PI phase, whereas the QP peak weakens in the PM phase. (c) Representation of the orbital splitting and their geometry. (d) Schematic of the experiments using an optical pump and different probes: trXRD, trPES and TRR.
(a) Time evolution of the intensity difference at −0.1 eV, the curve is fitted with a double exponential. (b) PES intensity difference for Δt=50 fs, 400 fs and 2 ps are shown for the PI phase as well as the equilibrium temperature difference from Fig. 1. The 50 and 400 fs differences show that the spectral weight is transferred inside the Mott gap, differently from a purely thermal effect. This non-thermal distribution relaxes within 2 ps. (c) Orbital character of the DOS near EF extracted from ref. 22. (d–f) Same as (a–c) but for the PM phase. The time evolution is fitted with a double exponential for the energy above EF.
Before exploring the behaviour of the system after photoexcitation, we present in Fig. 1 the photoemission responses of the PI and PM phases at different temperatures, which give us reference energy distribution curves (EDCs) for the system at equilibrium. In the PM phase the weight near EF increases with decreasing temperatures, which is consistent with the expected behaviour of the QP25,29. In the PI phase, the temperature increase fills the gap, which is consistent with the results from Mo et al.30. The temperature difference between 200 and 220 K, ΔT=20 K, matches the estimated temperature rise brought by the pump laser pulse for the fluence used in our pump–probe photoemission experiments (see Supplementary Notes 1 and 2 and Supplementary Figs 1–3). Therefore, the difference curves between high and low-temperature spectra at fixed doping may serve to compare the non-equilibrium spectra with reference to the thermal ones.
The non-equilibrium electron dynamics has been studied with pump–probe photoemission. The differences between positive and negative time delays are shown in Fig. 2a–c for the PI phase. As representative of the time evolution, we consider the timescan at −0.1 eV below EF (Fig. 2a), whose decay can be fitted with two exponentials. The details on the fitting procedure can be found in the Supplementary Note 3 and Supplementary Fig. 4. The first exponential with a 76±6 fs decay time is limited by our time resolution, corresponds to the hot electron relaxation after photoexcitation and clearly indicates a strong electron-phonon coupling. We associate the second longer timescale of 1.7±0.3 ps with the lifetime of a transient state, as suggested by comparing the EDCs at 50 fs, 400 fs and 2 ps with the thermal differences at equilibrium (black). At 50 fs delay (red curve) an increase in spectral weight is clearly visible both below and above EF, an evidence of creation of in-gap states. The EDC cannot be fitted with a Fermi-Dirac distribution, since the system is still strongly out-of-equilibrium. The 400 fs delay spectrum has instead no weight above EF: the excess electrons have cooled down. Nevertheless, the spectrum still deviates from the equilibrium one, in particular at −0.1 eV binding energy, indicating that, even though the electrons have relaxed, the state is different from the thermal configuration. A spectral difference equivalent to the thermal state at equilibrium can instead be found after 2 ps, when the transient state has fully relaxed.
Figure 2d–f reports the photoexcited behaviour of pure V2O3 (PM) at the same fluence of 1.8 mJ cm−2. The timescan at 0.1 eV above EF (Fig. 2d) shows a fast decay with a characteristic time of 70±6 fs (limited by the time resolution) and a slower one of 1.8±0.4 ps, similar to the time constants found in the PI phase. Indeed, the EDC differences at 50 and 400 fs delays are compatible with the hot electrons not being thermalized at 50 fs and almost thermalized at 400 fs.
The observed spectral changes obtained around EF by keeping the sample at T and photoexciting with a pump pulse cannot be ascribed to heating, but rather to a genuine non-thermal transient state31,32. In particular, both spectra at 50 and 400 fs (Fig. 2e) suggest that there is more weight both below and above EF in the photoexcited state at temperature T than in the equilibrium state at T+ΔT. Therefore, the reduction of density of states around EF is not compatible with a thermally excited configuration. This non-thermal state relaxes in 2 ps, similarly to the PI phase.
Time-resolved reflectivity
Further evidence in support of a transient non-thermal phase comes from the lattice. In Fig. 3 we present TRR measurements that provide information on the transient response of the fully symmetric A1g optical phonon, which corresponds to the breathing of one entity of V2O3 as shown in Fig. 1. Consistently with previous studies33,34, we observe an electronic excitation peak lasting about 200 fs, similar to the trPES response observed in Fig. 2. The succeeding coherent oscillations can be analysed by Fourier transform, which is compared in Fig. 3b,c with the A1g mode measured with Raman spectroscopy at equilibrium. Surprisingly, the mode displays a blue-shift of up to 14% compared with the equilibrium frequency for both PI and PM phases. Such a blue-shift, that is, a phonon hardening, is certainly non-thermal in nature. Indeed a temperature increase causes instead softening and consequently a red-shift35. Hardening of the A1g phonon actually corresponds to a decrease of the average distance between the two closest vanadium atoms, d(V1−V4)20. It should be underlined that this coherent phonon hardening is present for both the PM and PI phases, and that its decoherence time is about 2 ps: these features are in full agreement with the behaviour observed for the electronic degrees of freedom with trPES (Fig. 2). There is consequently a strong evidence of a transient phase that does not correspond to any equilibrium phase of the system, involving both the electronic and lattice structure and present in both PM and PI phases.
(a) TRR traces for (V1−xCrx)2O3 (x=0.028 PI and x=0 PM) for a fluence of 8 mJ cm−2: the A1g coherent phonon is clearly visible. (b,c) Fast Fourier transform of TRR traces compared with equilibrium Raman spectroscopy for the PM phase and PI phase, respectively. The A1g pump–probe frequencies (full) present a clear blue-shift compared with the equilibrium frequency (dashed) in both phases. (d) trXRD measurements in the PI phase for a fluence of 8 mJ cm−2, showing the pump–probe diffraction peak intensities for the Bragg reflections (116) and (024). The solid lines are the simulation as explained in text. (e) The calculated structure factor versus the shortest vanadium distance (V1−V4). The black dots represent the minimum distance observed extracted from d.
Time-resolved X-ray diffraction
In order to verify our interpretation on the nature of this transient phonon blue-shift, we performed a trXRD study on the same crystals used for the trPES and TRR measurements. The effective fluence was only slightly higher than in trPES because the probing depth of XRD is much higher than PES: since the behaviour of the trPES signal is linear versus fluence (see Supplementary Fig. 5) the results among the different experimental methods can be safely compared because we are in the same excitation regime.
In Fig. 3d,e we present the time-dependent intensity of the Bragg reflections (116) and (204) for the PI phase. The peak positions do not change until 4 ps, when the lattice parameters start being modified by the onset of the acoustic wave (as discussed in Supplementary Note 4 and Supplementary Fig. 6). Here we focus on the behaviour during the first few picoseconds, when the intensities of both Bragg reflections vary, while the lattice parameters are constant. Supposing that the symmetry of the crystal stays the same, the diffracted intensity can be simulated by a change of the vanadium Wyckoff position, ZV, and a Debye–Waller factor18, while keeping the V1—O1 distance constant. The change of the oxygen Wyckoff position affect the peak intensity of less than 0.02% for the (116) and about 1% for the (024) peak. The distance of the nearest vanadium atoms is given by the relation d(V1−V4)=(2ZV−0.5)c, where c is the lattice constant. The (116) and (024) structure factors vary in opposite directions with ZV. We find that, d(V1−V4) goes from 2.744 Å to a minimum value of 2.71 Å before 1 ps (d(V1−V4)PM=2.69 Å). The Debye–Waller factor is responsible for only 0.1% of the intensity change before 4 ps. After 4 ps, due to the lattice expansion, the changes in structure factor are no longer sufficient to explain the experimental curves because the peak position also starts changing (see Supplementary Fig. 6). The trXRD response was not able to resolve the coherent lattice oscillations, due to limits in the signal-to-noise levels attainable during the measurements, but it does confirm that the blue-shift in the coherent phonon frequency is related to a transient reduction of the average distance d(V1−V4). By comparing the temporal evolution of the different experimental results, the TRPES measurements show that the electronic structure is modified faster, and that the lattice deformation follows—which is expected for a prototype Mott system. The resulting non-thermal state is visibly more metallic in the PI phase, and seems most likely more delocalized in the PM one as well. In both cases, this state is stabilized by a transient lattice deformation that shortens the distance between the two nearest vanadium atoms and consequently increases the covalent bonding between the a1g orbitals. The fact that trXRD gives a slightly longer relaxation time with respect to trPES can be explained by the different probing depths of the two techniques6,36.
Discussion
In V2O3 the eσ orbital lie around 3 eV above EF (ref 20, 22; see Supplementary Fig. 7). Therefore, the most favourable transition with a 1.5 eV optical excitation is the transition from  to a1g, which is dipole-active. Figure 2c,f shows the orbital nature of the bands near EF, which are affected by the pump pulse. We considered a three-band Hubbard model at one-third filling for the t2g orbitals with the tight-binding hopping parameters of ref. 20, and analysed this model by means of the HF approximation22 using as control parameter, after a Legendre transform, the occupancy difference between
to a1g, which is dipole-active. Figure 2c,f shows the orbital nature of the bands near EF, which are affected by the pump pulse. We considered a three-band Hubbard model at one-third filling for the t2g orbitals with the tight-binding hopping parameters of ref. 20, and analysed this model by means of the HF approximation22 using as control parameter, after a Legendre transform, the occupancy difference between  and a1g orbitals. In order to describe an insulator within an independent particle scheme as HF we had to allow for magnetism; our insulator is thus closer to the antiferromagnetic insulator phase low-temperature phase rather than to the high-temperature PI22. Within HF, the total energy, shown in Fig. 4a, has two minima, a stable one at
and a1g orbitals. In order to describe an insulator within an independent particle scheme as HF we had to allow for magnetism; our insulator is thus closer to the antiferromagnetic insulator phase low-temperature phase rather than to the high-temperature PI22. Within HF, the total energy, shown in Fig. 4a, has two minima, a stable one at  describes the insulator and a metastable minimum at
describes the insulator and a metastable minimum at  that instead represents a metal. In Fig. 4b we plot the density of states for three different values of n, two in the insulating phase and one in the metal. We modelled the experiment in the PI phase starting from a Slater determinant that describes the HF insulator with a number of electrons transferred from the valence band of mostly
that instead represents a metal. In Fig. 4b we plot the density of states for three different values of n, two in the insulating phase and one in the metal. We modelled the experiment in the PI phase starting from a Slater determinant that describes the HF insulator with a number of electrons transferred from the valence band of mostly  character to the conduction one, with a1g character, and studied its time evolution within time-dependent HF.
character to the conduction one, with a1g character, and studied its time evolution within time-dependent HF.
(a) Hatree–Fock total energy as function of the occupancy difference between  and a1g orbitals (the total occupancy is 2). (b) DOS for different occupancies of the a1g. (c) Schematic view of the proposed mechanism involved in the photoexcitation of a Mott material, where the a1g states lower in energy both of the PM and PI phases.
and a1g orbitals (the total occupancy is 2). (b) DOS for different occupancies of the a1g. (c) Schematic view of the proposed mechanism involved in the photoexcitation of a Mott material, where the a1g states lower in energy both of the PM and PI phases.
We find it is enough to transfer ∼0.13 electrons to the conduction band to drive the system into the metastable metallic phase, as pictorially drawn in Fig. 4a, which is consistent with the experimental excitation that are 8% for a fluence of 8 mJ cm−2 in the trXRD and TRR experiments and 3.1% for the trPES. In other words, the non-thermal phase appears in this theoretical scenario as a metastable state that pre-exists in equilibrium and can be nucleated within the stable insulator through the photoexcitation. Since time-dependent HF does not account for dissipation, we cannot describe the subsequent break-up of the metastable metal nuclei back into the stable insulator, which experimentally occurs after few ps. The a1g orbitals being bonding, an overpopulation would bring the nearest vanadium atoms together. A LDA+U calculation with such an overpopulation of the a1g orbitals is able to capture the observed phonon hardening (see Supplementary Note 5 and Supplementary Figs 8–10).
With a combined experimental and theoretical approach, we show that the ultrafast response of the prototype Mott–Hubbard compound (V1−xCrx)2O3 is characterized by a non-thermal transient phase in which the system remains trapped before relaxing to the final thermal state. The formation of this non-thermal phase is very fast for both PM and PI—faster than our experimental time resolution—and it is eminently electronic in nature, being driven by a transient overpopulation of a bonding a1g orbital. A selective lattice deformation, strikingly highlighted by the A1g phonon hardening, further stabilizes this non-thermal transient phase, whose lifetime grows up to few ps: this direct comparative analysis of the evolution of the metallic and insulating phases is relevant for all the efforts aiming at photoinducing phase transitions in correlated materials, including possible technological applications like ultrafast switches. Our results thus show that a selective electron–lattice coupling can play an important role in out-of-equilibrium Mott systems, even though the main actor remains the strong correlation, and appear to be of very general validity, suggesting that similar non adiabatic pathways can be found in other multiband Mott compounds following excitation with ultrafast light pulses.
Methods
Samples
All the (V1−xCrx)2O3 samples used in our experiments are high-quality single crystals from Purdue University. They were oriented using Laue and X-ray diffraction, and cut along the (001) plane. For both the X-ray diffraction and the TRR measurements the samples were mechanically polished in order to have a flat surface. For all this specimens we could consistently observe nice coherent phonon oscillations, in agreement with previous studies33, which indicates a good crystal quality and rules out spurious effects in comparison with photoemission results. For the photoemission experiments the samples were cleaved along the (001) plane, where the QP photoelectron yield is most pronounced for the metallic phase25. All time-resolved measurements were performed at 200 K.
Time-resolved photoelectron spectroscopy
trPES measurements were performed on the FemtoARPES set-up37. A Ti:sapphire laser delivers 35 fs, 1.58 eV pulses that are split in two: one part is used to generate the fourth harmonic for the ultraviolet photoemission probe the rest serves for the pump pulses to excite the material. The original repetition rate is 250 kHz but it was reduced by a factor four by using a chopper in order to avoid residual heat. The energy resolution is better than 70 meV and the time resolution is better than 80 fs. The photoemission spectra were taken around ΓZ25. The (V1−xCrx)2O3 samples were oriented to have the [001] direction in the hexagonal notation perpendicular to the surface, and along the analyser axis. The samples were cleaved in situ in order to obtain a clean surface.
Time-resolved reflectivity
The TRR experiments were performed with a 1 kHz Ti:sapphire laser, which delivers 45 fs, 1.55 eV pulses. A near-normal incidence geometry was used and the pump and probe beams were cross-polarized. The background was subtracted before performing the Fast Fourier transform (FFT). The experiments were performed at 200 K.
Time-resolved X-ray diffraction
trXRD measurements were performed with sub-ps time resolution at the x-ray pump probe (XPP) end-station of the Linac coherent light source38. The incidence angle for the 8 keV X-ray beam was 0.6°, while for the optical laser beam it was 12°: this geometry allowed us to match the penetration depths and retain a temporal resolution of the order of 200 fs. The estimated penetration depth for the X-rays is 120 nm, whereas it is 88 nm for the optical laser. The sample was cooled down to 200 K with a cryo-jet. The different Bragg reflections were observed using a two-dimensional detector.
The Bragg peak intensity was measured by integrating over a 20 × 20 pixels wide region centred around the peak. Due to monochromatization of the X-ray beam, any energy jitter from the self amplified spontaneous emission (SASE) process results in an X-ray intensity fluctuation on the sample. The flux and the position of the incident photons were measured by intensity-position monitors. A key point in analysing the data was choosing an intensity and position range, which optimizes the signal-to-noise ratio: this was done by analysing the Bragg reflection behaviour for negative time delays. The best results were obtained by cutting off the 20% lowest shots and the 5% highest, as well as filtering on the positions that deviate more than one s.d. in x and y. The data were then corrected for the delay-time jitter using the LCLS timing-tool. We chose a time bin of 50 fs, which gives an average of ∼106 photons per delay.
Data availability
The data that support the findings of this study are available from the corresponding authors upon reasonable request
Additional information
How to cite this article: Lantz, G. et al. Ultrafast evolution and transient phases of a prototype out-of-equilibrium Mott–Hubbard material. Nat. Commun. 8, 13917 doi: 10.1038/ncomms13917 (2017).
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
Mott, N. & Peierls, R. Discussion of the paper by de Boer and Verwey. Proc. Phys. Soc. 49, 416–422 (1937).
Imada, M., Fujimori, A. & Tokura, Y. Metal-insulator transitions. Rev. Mod. Phys. 70, 1039–1263 (1998).
Goodenough, J. B. The two components of the crystallographic transition in VO2 . J. Solid State Chem. 3, 490–500 (1971).
McWhan, D. B., Rice, T. M. & Remeika, J. P. Mott transition in Cr-Doped V2O3 . Phys. Rev. Lett. 23, 1384 (1969).
Cavalleri, A. et al. Femtosecond structural dynamics in VO2 during an ultrafast solid-solid phase transition. Phys. Rev. Lett. 87, 237401 (2001).
Wegkamp, D. et al. Instantaneous band gap collapse in photoexcited monoclinic VO2 due to photocarrier doping. Phys. Rev. Lett. 113, 216401 (2014).
Kübler, C. et al. Coherent structural dynamics and electronic correlations during an ultrafast insulator-to-metal phase transition in VO2 . Phys. Rev. Lett. 99, 116401 (2007).
Perfetti, L. et al. Time evolution of the electronic structure of 1 T-TaS2 through the insulator-metal transition. Phys. Rev. Lett. 97, 067402 (2006).
Yoshida, R. et al. Ultrafast photoinduced transition of an insulating VO2 thin film into a nonrutile metallic state. Phys. Rev. B 89, 205114 (2014).
Morrison, V. R. et al. A photoinduced metal-like phase of monoclinic VO2 revealed by ultrafast electron diffraction. Science 346, 445–448 (2014).
Eckstein, M. & Werner, P. Photoinduced states in a Mott insulator. Phys. Rev. Lett. 110, 126401 (2013).
Liu, M. et al. Photoinduced phase transitions by time-resolved far-infrared spectroscopy in V2O3 . Phys. Rev. Lett. 107, 066403 (2011).
Lupi, S. et al. A microscopic view on the Mott transition in chromium-doped V2O3 . Nat. Commun. 1, 105 (2010).
Kim, K. W. et al. Ultrafast transient generation of spin-density-wave order in the normal state of BaFe2As2 driven by coherent lattice vibrations. Nat. Mater. 11, 497–501 (2012).
Mansart, B. et al. Observation of a coherent optical phonon in the iron pnictide superconductor BaFe2As2 . Phys. Rev. B 80, 172504 (2009).
Rohwer, T. et al. Collapse of long-range charge order tracked by time-resolved photoemission at high momenta. Nature 471, 490–493 (2011).
Hellmann, S. et al. Time-domain classification of charge-density-wave insulators. Nat. Commun. 3, 1069 (2012).
Johnson, S., Vorobeva, E., Beaud, P., Milne, C. & Ingold, G. Full Reconstruction of a crystal unit cell structure during coherent femtosecond motion. Phys. Rev. Lett. 103, 205501 (2009).
Boschetto, D. et al. Real-time observation of interlayer vibrations in bilayer and few-layer graphene. Nano. Lett. 13, 4620–4623 (2013).
Saha-Dasgupta, T. et al. Electronic structure of V2O3: Wannier orbitals from LDA-NMTO calculations. Preprint at http://arxiv.org/abs/0907.2841 (2009).
Poteryaev, A. et al. Enhanced crystal-field splitting and orbital-selective coherence induced by strong correlations in V2O3 . Phys. Rev. B 76, 085127 (2007).
Grieger, D. & Fabrizio, M. Low-temperature magnetic ordering and structural distortions in vanadium sesquioxide V2O3 . Phys. Rev. B 92, 075121 (2015).
Park, J. et al. Spin and orbital occupation and phase transitions in V2O3 . Phys. Rev. B 61, 11506 (2000).
Mo, S.-K. et al. Photoemission study of V2O3 . Phys. Rev. B 74, 165101 (2006).
Rodolakis, F. et al. Quasiparticles at the Mott transition in V2O3: wave vector dependence and surface attenuation. Phys. Rev. Lett. 102, 066805 (2009).
Rodolakis, F. et al. Inequivalent routes across the Mott transition in V2O3 explored by X-ray absorption. Phys. Rev. Lett. 104, 047401 (2010).
Ichikawa, H. et al. Transient photoinduced ‘hidden’ phase in a manganite. Nat. Mater. 10, 101–105 (2011).
Stojchevska, L. et al. Ultrafast switching to a stable hidden quantum state in an electronic crystal. Science 344, 177–180 (2014).
Baldassarre, L. et al. Quasiparticle evolution and pseudogap formation in V2O3: an infrared spectroscopy study. Phys. Rev. B 77, 113107 (2008).
Mo, S.-K. et al. Filling of the Mott-Hubbard gap in the high temperature photoemission spectrum of (V0.972Cr0.028)2O3 . Phys. Rev. Lett. 93, 076404 (2004).
Wall, S. et al. Quantum interference between charge excitation paths in a solid-state Mott insulator. Nat. Phys. 7, 114–118 (2010).
Novelli, F. et al. Witnessing the formation and relaxation of dressed quasi-particles in a strongly correlated electron system. Nat. Commun. 5, 5112 (2014).
Misochko, O. et al. Optical study of the Mott transition in V2O3: comparison of time- and frequency-domain results. Phys. Rev. B 58, 12789–12794 (1998).
Mansart, B., Boschetto, D., Sauvage, S., Rousse, A. & Marsi, M. Mott transition in Cr-doped V2O3 studied by ultrafast reflectivity: electron correlation effects on the transient response. Europhys. Lett. 92, 37007 (2010).
Tatsuyama, C. & Fan, H. Raman scattering and phase transitions in V2O3 and (V1−xCrx)2O3 . Phys. Rev. B 21, 2977–2983 (1980).
Lantz, G. et al. Surface effects on the Mott-Hubbard transition in archetypal V2O3 . Phys. Rev. Lett. 115, 236802 (2015).
Faure, J. et al. Full characterization and optimization of a femtosecond ultraviolet laser source for time and angle-resolved photoemission on solid surfaces. Rev. Sci. Instrum. 83, 043109 (2012).
Chollet, M. et al. The X-ray pump-probe instrument at the linac coherent light source. J. Synchrotron. Radiat. 22, 503–507 (2015).
Acknowledgements
This work has been partly supported by the EU under the contract Go Fast (Grant No. 280555) and under the ERC project No. 692670. G.L., N.M., L.P., E.P. and M.M. acknowledge financial support by Investissement d’Avenir Labex PALM (ANR-10-LABX-0039-PALM), by the Equipex ATTOLAB (ANR11-EQPX0005-ATTOLAB) and by the Région Ile-de-France through the programme DIM OxyMORE. D.B. acknowledges the financial support of the French Procurement Agency (DGA) of the French Ministry of Defense. The Advanced Light Source is supported by the Director, Office of Science, Office of Basic Energy Sciences, of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231. Use of the Linac Coherent Light Source (LCLS), SLAC National Accelerator Laboratory is supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences under Contract No. DE-AC02-76SF00515.
Author information
Authors and Affiliations
Contributions
G.L., E.P. and L.P. performed the trPES experiments. B.M., E.P. and D.B. performed the TRR experiments. G.L., D.B., E.P., N.M., V.L.R.J., D.B., C.L., S.R., J.-P.R. and M.M. carried out the trXRD experiments, with the contribution of T.E.G., M.P.H., Z.H., S.S. and M.C. N.N., G.L., N.M. and V.L.R.J. performed the trXRD analysis. D.G. and M.F. carried out the theoretical calculations and interpretation. G.L., M.F. and M.M. wrote the article, with inputs from all the authors. M.M. conceived and coordinated the project.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures 1-10, Supplementary Notes 1-5 and Supplementary References (PDF 463 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Lantz, G., Mansart, B., Grieger, D. et al. Ultrafast evolution and transient phases of a prototype out-of-equilibrium Mott–Hubbard material. Nat Commun 8, 13917 (2017). https://doi.org/10.1038/ncomms13917
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms13917
This article is cited by
-
Picosecond volume expansion drives a later-time insulator–metal transition in a nano-textured Mott insulator
Nature Physics (2024)
-
Terahertz displacive excitation of a coherent Raman-active phonon in V2O3
Communications Physics (2022)
-
Nanoscale self-organization and metastable non-thermal metallicity in Mott insulators
Nature Communications (2022)
-
Time-resolved photoemission of infinitely periodic atomic arrangements: correlation-dressed excited states of solids
npj Computational Materials (2020)
-
Monitoring ultrafast metallization in LaCoO3 with femtosecond soft x-ray spectroscopy
Communications Physics (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.