Abstract
Repeated observations inhibit the coherent evolution of quantum states through the quantum Zeno effect. In multi-qubit systems this effect provides opportunities to control complex quantum states. Here, we experimentally demonstrate that repeatedly projecting joint observables of multiple spins creates quantum Zeno subspaces and simultaneously suppresses the dephasing caused by a quasi-static environment. We encode up to two logical qubits in these subspaces and show that the enhancement of the dephasing time with increasing number of projections follows a scaling law that is independent of the number of spins involved. These results provide experimental insight into the interplay between frequent multi-spin measurements and slowly varying noise and pave the way for tailoring the dynamics of multi-qubit systems through repeated projections.
Similar content being viewed by others
Introduction
The quantum Zeno effect restricts the evolution of repeatedly observed quantum systems. For a two-dimensional system the state simply is frozen in one of two eigenstates of the measurement operator1,2,3,4,5,6,7,8,9,10. In multi-dimensional systems; however, Zeno subspaces are formed that can contain complex quantum states and dynamics: repeated observations create a barrier that blocks coherent evolution between subspaces, but leaves coherences and dynamics within those subspaces intact11. Analogous effects can also be realized through coherent control pulses or strong driving fields that decouple transitions between the subspaces12,13,14,15,16,17,18,19. Pioneering experiments have highlighted that the non-trivial dynamics in Zeno subspaces can be used to prepare exotic quantum states20,21,22,23,24. However, the opportunities to tailor the dynamics of multi-qubit systems by restricting coherent evolution have remained unexplored.
Here we show that repeated multi-spin projections on individually controlled spins create quantum Zeno subspaces that can encode multiple logical qubits while suppressing dephasing caused by the environment. We realize these repeated projections for up to three nuclear spins in diamond using the optical transition of a nearby electron spin. We then encode up to two logical qubits—including entangled states of logical qubits—and show that increasing the frequency of the projections supresses the dephasing of quantum states. Finally, we theoretically derive and experimentally verify a scaling law that shows that the increase in dephasing time is independent of the number of spins involved.
Results
Experimental system and sequence
Our system consists of three 13C spins (I=½) surrounding a single nitrogen vacancy (NV) centre (|0〉NV : ms=0 and |1〉NV : ms=−1) in diamond (see Supplementary Note 1). The natural evolution of the 13C spins is dominated by dephasing due to the slowly fluctuating surrounding bath of 13C spins (dephasing times  =12.4(9), 8.2(7) and 21(1) ms for spin 1, 2 and 3, respectively)25. Because the fluctuations are quasi-static, the Hamiltonian in a given experiment is
=12.4(9), 8.2(7) and 21(1) ms for spin 1, 2 and 3, respectively)25. Because the fluctuations are quasi-static, the Hamiltonian in a given experiment is  , with k the number of spins and the detuning Δi for spin i drawn from a Gaussian distribution with
, with k the number of spins and the detuning Δi for spin i drawn from a Gaussian distribution with  . We denote the Pauli operators as
. We denote the Pauli operators as  ,
,  ,
,  and the identity as
and the identity as  .
.
The quantum Zeno effect arises when an observable  is projected (super-operator
is projected (super-operator  ). Here we consider dichotomic observables with eigenvalues ±1. A projection leaves the system’s density matrix (ρs) in block-diagonal form with respect to the projectors
). Here we consider dichotomic observables with eigenvalues ±1. A projection leaves the system’s density matrix (ρs) in block-diagonal form with respect to the projectors  (ref. 11):
(ref. 11):

Repeatedly projecting observable  thus inhibits coherent evolution between the two eigenspaces of
thus inhibits coherent evolution between the two eigenspaces of  . We choose joint multi-spin observables of the form
. We choose joint multi-spin observables of the form  , which anti-commute with all terms in the Hamiltonian H, so that rapid projections ideally result in the effective Zeno Hamiltonian
, which anti-commute with all terms in the Hamiltonian H, so that rapid projections ideally result in the effective Zeno Hamiltonian  (ref. 11). Applying these projections therefore suppresses dephasing for each nuclear spin, but leaves quantum states and driven dynamics inside the two subspaces untouched (Fig. 1a).
(ref. 11). Applying these projections therefore suppresses dephasing for each nuclear spin, but leaves quantum states and driven dynamics inside the two subspaces untouched (Fig. 1a).
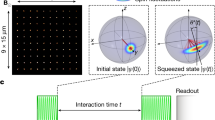
(a) Quantum Zeno subspaces. The state space of a quantum system is divided into two subspaces (yellow boxes) of an observable  . Plus and minus signs indicate eigenvalues of the associated operator. Coherent transitions between the two subspaces occur while the system is unperturbed (top, red arrows) but are strongly inhibited if
. Plus and minus signs indicate eigenvalues of the associated operator. Coherent transitions between the two subspaces occur while the system is unperturbed (top, red arrows) but are strongly inhibited if  is repeatedly projected (bottom). (b) Experimental sequence. After initialization in |ψ〉, N equidistantly distributed projections M(
is repeatedly projected (bottom). (b) Experimental sequence. After initialization in |ψ〉, N equidistantly distributed projections M( ) (see equation (1)) are applied during a total evolution time τ and the state of the system is read out. (c) Realization of
) (see equation (1)) are applied during a total evolution time τ and the state of the system is read out. (c) Realization of  for three nuclear spins. First, the state of the nuclear spins (yellow) is entangled with the ancilla electron-spin state (purple). Second, the electron spin is projected and reinitialized in |1〉NV (see also d) through a long 30 μs optical pumping pulse to |0〉NV and a subsequent microwave π-pulse (X). Such a long laser excitation pulse ensures that the NV is projected. The x and y gates are π/2 rotations around the X and Y axes, respectively. Controlled gates indicate that the direction is determined by the electron spin28. See Supplementary Fig. 3 for pulse sequences for projections on one and two spins. (d) Relevant electron spin levels for optical re-pumping through selective resonant excitation of |1〉NV to |e〉NV. We prepare the nuclear spin states in the 〈
for three nuclear spins. First, the state of the nuclear spins (yellow) is entangled with the ancilla electron-spin state (purple). Second, the electron spin is projected and reinitialized in |1〉NV (see also d) through a long 30 μs optical pumping pulse to |0〉NV and a subsequent microwave π-pulse (X). Such a long laser excitation pulse ensures that the NV is projected. The x and y gates are π/2 rotations around the X and Y axes, respectively. Controlled gates indicate that the direction is determined by the electron spin28. See Supplementary Fig. 3 for pulse sequences for projections on one and two spins. (d) Relevant electron spin levels for optical re-pumping through selective resonant excitation of |1〉NV to |e〉NV. We prepare the nuclear spin states in the 〈 〉=+1 subspace and associate this subspace with the electron state |0〉NV in the entangling sequence so that the optical projection ideally never excites the NV centre.
〉=+1 subspace and associate this subspace with the electron state |0〉NV in the entangling sequence so that the optical projection ideally never excites the NV centre.
To investigate quantum Zeno subspaces we use the following experimental sequence (Fig. 1b). We first initialize the nuclear spins in the desired state and prepare the electron spin in |1〉NV. Crucially, leaving the electron in |1〉NV creates a different frequency shift for each of the three 13C spins that suppresses resonant flip-flop interactions among the 13C spins during idle time26. We then apply a total of N projections that are equally distributed in time. Finally, the nuclear spin state is read out using the electron spin as an ancilla (refs 27, 28, 29, 30, 31, 32). Here we consider the case of an even number of projections. The results for an odd number of projections N give rise to additional effects at long evolution times due to the time-correlations in the noise and are discussed in Supplementary Fig. 1. The total evolution time τ is defined from the end of the initialization to the start of the read-out. We subtract the time that control operations are applied to the nuclear spins (averaged over all spins), as dephasing might be suppressed during driving (for a comparison see Supplementary Fig. 2).
We experimentally realize repeated multi-spin projections on the 13C spins by using the NV electron spin as an ancilla spin (Fig. 1c). First, we entangle the NV electron spin state with the projections on the eigenspaces of  (〈
(〈 〉=+1 or −1), so that the combined state is
〉=+1 or −1), so that the combined state is  (refs 25, 33). Second, we apply an optical excitation that is resonant only if the electron-spin state is |1〉NV (‘reset’)25, which projects the quantum state and re-initializes the NV electron spin in |0〉NV through optical pumping (Fig. 1d). Note that it is not required to extract or record the outcome of the optical measurement. To mitigate extra dephasing caused by the stochastic nature of the optical re-initialization (time constant of ∼1 μs), we use 13C spins with a NV-13C hyperfine coupling that is small compared with the inverse of the time constant for re-initialization (all couplings are below 2π·50 kHz)34,35. In addition, we design the gate sequence, so that |0〉NV is associated with the subspace of the initial nuclear state: ideally the electron spin is never optically excited and the projection constitutes a null measurement.
(refs 25, 33). Second, we apply an optical excitation that is resonant only if the electron-spin state is |1〉NV (‘reset’)25, which projects the quantum state and re-initializes the NV electron spin in |0〉NV through optical pumping (Fig. 1d). Note that it is not required to extract or record the outcome of the optical measurement. To mitigate extra dephasing caused by the stochastic nature of the optical re-initialization (time constant of ∼1 μs), we use 13C spins with a NV-13C hyperfine coupling that is small compared with the inverse of the time constant for re-initialization (all couplings are below 2π·50 kHz)34,35. In addition, we design the gate sequence, so that |0〉NV is associated with the subspace of the initial nuclear state: ideally the electron spin is never optically excited and the projection constitutes a null measurement.
Quantum Zeno effect for a single spin
To illustrate the quantum Zeno effect and to benchmark our system, we first consider a single 13C spin and study the dephasing of the superposition state  for
for  (Fig. 2a). We initialize the 13C spin in |X〉 with an initial state fidelity of 0.95(2) and apply up to N=16 projections. For a fixed total evolution time of 40 ms, we observe a significant increase of the state fidelity with an increasing number of projections (Fig. 2b). The complete time traces show that the dephasing time increases as more projections are applied (Fig. 2c); the superposition state is protected by the quantum Zeno effect. In this example, however, the Zeno subspaces contain just a single state and therefore cannot encode general quantum states.
(Fig. 2a). We initialize the 13C spin in |X〉 with an initial state fidelity of 0.95(2) and apply up to N=16 projections. For a fixed total evolution time of 40 ms, we observe a significant increase of the state fidelity with an increasing number of projections (Fig. 2b). The complete time traces show that the dephasing time increases as more projections are applied (Fig. 2c); the superposition state is protected by the quantum Zeno effect. In this example, however, the Zeno subspaces contain just a single state and therefore cannot encode general quantum states.
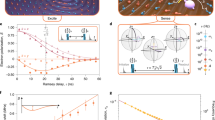
(a) Quantum Zeno subspaces for a single nuclear spin (spin 1) and  . Each eigenspace of
. Each eigenspace of  consists of one state (|X〉 or |−X〉) with the respective eigenvalue indicated by the circled +/− signs. (b) State fidelity for |X〉 after τ=40 ms. The fidelity initially increases with the number of projections N. (c) The complete time traces for the storage of |X〉 show that the dephasing time increases with the number of projections. The curves are fits to the theoretically expected fidelity (see equation (3)). All data are corrected for the final read-out fidelity (Supplementary Fig. 4 and Supplementary Note 3). All error bars are 1 s.d.
consists of one state (|X〉 or |−X〉) with the respective eigenvalue indicated by the circled +/− signs. (b) State fidelity for |X〉 after τ=40 ms. The fidelity initially increases with the number of projections N. (c) The complete time traces for the storage of |X〉 show that the dephasing time increases with the number of projections. The curves are fits to the theoretically expected fidelity (see equation (3)). All data are corrected for the final read-out fidelity (Supplementary Fig. 4 and Supplementary Note 3). All error bars are 1 s.d.
Preserving a logical qubit via quantum Zeno subspaces
We next investigate Zeno subspaces that can contain an arbitrary two-dimensional quantum state, that is, a complete logical quantum bit, by performing joint projections on two 13C spins. We set the joint-observable  , so that the four-dimensional state space is divided into two coherent two-level subspaces (Fig. 3a). In these subspaces a logical qubit, which can hold an arbitrary quantum state, can be defined as
, so that the four-dimensional state space is divided into two coherent two-level subspaces (Fig. 3a). In these subspaces a logical qubit, which can hold an arbitrary quantum state, can be defined as  , with
, with  and
and  , and with logical operators
, and with logical operators  and
and  . Note that logical qubit superposition states are generally entangled states of the two 13C spins.
. Note that logical qubit superposition states are generally entangled states of the two 13C spins.
(a) Schematic representation: the four-dimensional state-space of two 13C spins (spin 1 and 2) is divided into two subspaces by repetitively projecting  through entanglement with the ancilla spin. We define a logical quantum bit with logical operator
through entanglement with the ancilla spin. We define a logical quantum bit with logical operator  (dashed line) and associate
(dashed line) and associate  in
in  with the spin with the longest coherence time (spin 1). (b) Storing a logical quantum bit. The average logical state fidelity for the six logical input states, for example,
with the spin with the longest coherence time (spin 1). (b) Storing a logical quantum bit. The average logical state fidelity for the six logical input states, for example,  for |0〉L, as a function of time and for a varying number of projections N. To compare the results to the best possible decay for a single nuclear spin, we compare to the individual decay of spin 1 and eliminate potential systematic detunings by measuring
for |0〉L, as a function of time and for a varying number of projections N. To compare the results to the best possible decay for a single nuclear spin, we compare to the individual decay of spin 1 and eliminate potential systematic detunings by measuring  (instead of
(instead of  or
or  ). The dashed horizontal line is the classical limit of 2/3 (ref. 37). (c) Preserving two-spin entangled states. The two-spin state fidelity, averaged over the four entangled input states, indicates that general two-spin states in the subspace are preserved. Above the dashed horizontal line (F=0.5) the state is entangled. For N=2, 4 and 6 projections, entanglement is preserved longer than without projections. Solid lines are fits to equation (3) with the initial amplitude A, an offset and the effective dephasing time
). The dashed horizontal line is the classical limit of 2/3 (ref. 37). (c) Preserving two-spin entangled states. The two-spin state fidelity, averaged over the four entangled input states, indicates that general two-spin states in the subspace are preserved. Above the dashed horizontal line (F=0.5) the state is entangled. For N=2, 4 and 6 projections, entanglement is preserved longer than without projections. Solid lines are fits to equation (3) with the initial amplitude A, an offset and the effective dephasing time  as free parameters. Error bars are 1 s.d. and are smaller than the symbols.
as free parameters. Error bars are 1 s.d. and are smaller than the symbols.
We characterize the storage of arbitrary quantum states by preparing all six logical basis states  and averaging the final logical state fidelities36 (Fig. 3b). The logical qubit without projections shows the same decay as a single 13C spin, but with a slightly reduced initial fidelity (F=0.89(1)) due to the overhead of creating the entangled states |ψ〉L. Applying projections of the joint-observable
and averaging the final logical state fidelities36 (Fig. 3b). The logical qubit without projections shows the same decay as a single 13C spin, but with a slightly reduced initial fidelity (F=0.89(1)) due to the overhead of creating the entangled states |ψ〉L. Applying projections of the joint-observable  strongly suppresses the dephasing by the environment, while preserving the logical qubit states. As a result, the average state fidelity for the logical qubit surpasses the best 13C nuclear spin used, while still remaining above the threshold of 2/3 for the storage of quantum states37. This result demonstrates the suppression of the dephasing of a complete logical qubit through the quantum Zeno effect.
strongly suppresses the dephasing by the environment, while preserving the logical qubit states. As a result, the average state fidelity for the logical qubit surpasses the best 13C nuclear spin used, while still remaining above the threshold of 2/3 for the storage of quantum states37. This result demonstrates the suppression of the dephasing of a complete logical qubit through the quantum Zeno effect.
Interestingly, preserving the logical qubit does not actually require the coherence of the second spin to be maintained, as follows from the logical operator  . To show that the complete two-spin state is preserved, including entanglement between the two nuclear spins, we measure the average state fidelity with the ideal two-spin state for the four entangled initial states as a function of time (Fig. 3c). The duration for which genuine entanglement persists (two-spin state fidelity >0.5) is extended for N=2, 4 and 6 projections compared with the case without any projections, indicating that the barrier introduced by the projections inhibits dephasing for any two-spin state within the Zeno subspace.
. To show that the complete two-spin state is preserved, including entanglement between the two nuclear spins, we measure the average state fidelity with the ideal two-spin state for the four entangled initial states as a function of time (Fig. 3c). The duration for which genuine entanglement persists (two-spin state fidelity >0.5) is extended for N=2, 4 and 6 projections compared with the case without any projections, indicating that the barrier introduced by the projections inhibits dephasing for any two-spin state within the Zeno subspace.
Quantum Zeno subspaces with two logical qubits
Realizing Zeno subspaces with even more dimensions enables the exploration of complex states of multiple logical qubits within the subspaces. We include a third nuclear spin and set  to create a protected four-dimensional subspace, which can host two logical qubits defined by the logical operators
to create a protected four-dimensional subspace, which can host two logical qubits defined by the logical operators  and
and  (Fig. 4a). Each pure state within the
(Fig. 4a). Each pure state within the  =+1 subspace can be expressed in terms of the logical two-qubit states:
=+1 subspace can be expressed in terms of the logical two-qubit states:
(a) Schematic representation for three nuclear spins (spins 1–3) and  . Two four-dimensional subspaces are created (yellow box). For simplicity we only show the positive subspace, which contains states of the form
. Two four-dimensional subspaces are created (yellow box). For simplicity we only show the positive subspace, which contains states of the form  . Within this subspace two logical qubits are defined by the logical operators
. Within this subspace two logical qubits are defined by the logical operators  ,
,  and
and  ,
,  (blue and red boxes). (b) Logical state fidelities for three logical states: eigenstate |0,0〉L, superposition state |X,0〉L, and the entangled state |Φ+〉L. The results show that repeated projections of the three-spin operator
(blue and red boxes). (b) Logical state fidelities for three logical states: eigenstate |0,0〉L, superposition state |X,0〉L, and the entangled state |Φ+〉L. The results show that repeated projections of the three-spin operator  preserve the two logical qubits while inhibiting dephasing. Solid lines are fits to equation (3). The fidelities decay to different values for large τ because |Φ+〉L and |X,0〉L are eigenstates of operators of the form
preserve the two logical qubits while inhibiting dephasing. Solid lines are fits to equation (3). The fidelities decay to different values for large τ because |Φ+〉L and |X,0〉L are eigenstates of operators of the form  or one of its permutations, whose expectation values are unaffected by dephasing. Error bars are 1 s.d.
or one of its permutations, whose expectation values are unaffected by dephasing. Error bars are 1 s.d.

To investigate the inhibition of dephasing of the two logical qubits by repeated projections we prepare three different logical states: the logical eigenstate state |0,0〉L, the logical superposition state  and the entangled logical state
and the entangled logical state  . Preserving this set of states requires repeated projections of the three-spin operator
. Preserving this set of states requires repeated projections of the three-spin operator  , since they are not eigenstates of a single two-spin operator.
, since they are not eigenstates of a single two-spin operator.
The logical state fidelities for all three states show a clear prolongation of the decay times for N=2 and 4 three-spin projections (Fig. 4b). Moreover, for a range of evolution times, the absolute logical state fidelities are increased despite the initial loss of fidelity due to the complexity of the experimental sequence (33 two-qubit gates for N=4, which in total require 1,276 refocusing pulses on the electron spin). These results confirm that the introduced three-spin projections inhibit dephasing of the individual spins while preserving the two logical qubits in a quantum Zeno subspace.
Scaling law for the suppression of dephasing
To gain a detailed quantitative understanding of the quantum Zeno effect for multi-spin projections, we derive a complete analytical description for the evolution. We model the projections as instantaneous and the noise as a quasi-static Gaussian frequency detuning, independent for each nuclear spin. We find an analytic solution for the decay of the expectation value of observables that are sensitive to dephasing (for N projections and total evolution time τ):

Here A ≤ 1 is the initial amplitude determined by experimental fidelities and  is an effective joint decay rate of all involved spins. This result is valid for any system size, that is, number of spins, and number of projections N (both even and odd). A detailed derivation of equation (3) is given in Supplementary Note 2.
is an effective joint decay rate of all involved spins. This result is valid for any system size, that is, number of spins, and number of projections N (both even and odd). A detailed derivation of equation (3) is given in Supplementary Note 2.
We fit all experimental data in Figs 2, 3, 4 with A,  and an offset, to account for the fact that two out of six cardinal states are insensitive to dephasing, as free parameters. We find good agreement with the experimentally obtained dephasing curves (see Supplementary Table 1 for all fit values). To analyse the increase of the decay time with increasing number of projections, we compile the extracted values from all experiments with an even number of projections and with 1–3 nuclear spins in Fig. 5. The results reveal a scaling law that is independent of the number of spins involved, in good quantitative agreement with our theoretical model.
and an offset, to account for the fact that two out of six cardinal states are insensitive to dephasing, as free parameters. We find good agreement with the experimentally obtained dephasing curves (see Supplementary Table 1 for all fit values). To analyse the increase of the decay time with increasing number of projections, we compile the extracted values from all experiments with an even number of projections and with 1–3 nuclear spins in Fig. 5. The results reveal a scaling law that is independent of the number of spins involved, in good quantitative agreement with our theoretical model.
The fitted decay times for all measurements in this article (Figs 2, 3, 4) are compared with the theoretical decay time enhancement (solid line). All values are taken relative to the value without projections (N=0). The data are averaged according to the number of operators in the expectation values that are subject to dephasing (that is, the number of  and/or
and/or  ). Red: one operator. Blue: two operators. Orange: three operators (see Supplementary Fig. 5 for raw data). To show that the normalized decay time is independent of the number of nuclear spins, we distinguish data with a differing total number of nuclear spins. For instance, measurements of
). Red: one operator. Blue: two operators. Orange: three operators (see Supplementary Fig. 5 for raw data). To show that the normalized decay time is independent of the number of nuclear spins, we distinguish data with a differing total number of nuclear spins. For instance, measurements of  (with
(with  ) or
) or  (with
(with  ) are represented by separate data points. The theory curve is obtained by evaluating equation (3) up to N = 16 (see Supplementary Fig. 6). The obtained curve depends only on the functional shape of the underlying quasi-static noise spectrum. Error bars are 1 s.d.
) are represented by separate data points. The theory curve is obtained by evaluating equation (3) up to N = 16 (see Supplementary Fig. 6). The obtained curve depends only on the functional shape of the underlying quasi-static noise spectrum. Error bars are 1 s.d.
Discussion
In conclusion, we have observed that repeatedly projecting joint-observables of multi-spin systems creates quantum Zeno subspaces that can hold complex quantum states, and that these Zeno subspaces are resilient to environmental dephasing. While suppression of dephasing may also be achieved through alternative techniques such as coherent refocusing17,18,19, our results provide direct experimental insight into the physics of repeated multi-spin measurements and Zeno subspaces in low-frequency noise environments. The results are also of practical relevance in the context of quantum error correction and detection codes, in which errors are detected through repeated measurements of joint observables25,38,39. Moreover, the demonstrated methods pave the way for investigating the effect of repeated measurements in various noise environments, for example, non-Markovian noise, and for exploring and engineering complex dynamics of multi-qubit systems under tailored decoherence40,41,42,43.
Data availability
The data that support the findings of this study are available from the corresponding author upon request.
Additional information
How to cite this article: Kalb, N. et al. Experimental creation of quantum Zeno subspaces by repeated multi-spin projections in diamond. Nat. Commun. 7, 13111 doi: 10.1038/ncomms13111 (2016).
References
Misra, B. & Sudarshan, E. C. G. The Zeno’s paradox in quantum theory. J. Math. Phys. 18, 756–763 (1977).
Itano, W. M. et al. Quantum Zeno effect. Phys. Rev. A 41, 2295–2300 (1990).
Wolters, J. et al. Quantum Zeno phenomenon on a single solid-state spin. Phys. Rev. A 88, 020101(R) (2013).
Kakuyanagi, K. et al. Observation of quantum Zeno effect in a superconducting flux qubit. New J. Phys. 17, 063035 (2015).
Peise, J. et al. Interaction-free measurements by quantum Zeno stabilization of ultracold atoms. Nat. Commun. 6, 6811 (2015).
Slichter, D. H. et al. Quantum Zeno effect in the strong measurement regime of circuit quantum electrodynamics. New J. Phys. 18, 053031 (2016).
Patil, Y. S. et al. Measurement-induced localization of an ultracold lattice gas. Phys. Rev. Lett. 115, 140402 (2015).
Wilkinson, S. et al. Experimental evidence for non-exponential decay in quantum tunnelling. Nature 387, 575–577 (1997).
Fischer, M. C. et al. Observation of the quantum Zeno and anti-Zeno effects in an unstable system. Phys. Rev. Lett. 87, 040402 (2001).
Kondo, Y. et al. Using the quantum Zeno effect for suppression of decoherence. New J. Phys. 18, 013033 (2016).
Facchi, P. & Pascazio, S. Quantum Zeno subspaces. Phys. Rev. Lett. 89, 080401 (2002).
Facchi, P. et al. Unification of dynamical decoupling and the quantum Zeno effect. Phys. Rev. A 69, 032314 (2004).
Viola, L. & Lloyd, S. Dynamical suppression of decoherence in two-state quantum systems. Phys. Rev. A 58, 2733 (1998).
Dhar, D. et al. Preserving quantum states using inverting pulses: a super-Zeno effect. Phys. Rev. Lett. 96, 100405 (2006).
Zheng, W. et al. Experimental demonstration of the quantum Zeno effect in NMR with entanglement-based measurements. Phys. Rev. A 87, 032112 (2013).
Singh, H. et al. Experimental protection against evolution of states in a subspace via a super-Zeno scheme on a NMR quantum information processor. Phys. Rev. A 90, 052329 (2014).
Zhong, M. et al. Optically addressable nuclear spins in a solid with a six-hour coherence time. Nature 517, 177–180 (2015).
Maurer, P. C. et al. Room-temperature quantum bit memory exceeding one second. Science 336, 1283–1286 (2012).
de Lange, G. et al. Universal dynamical decoupling of a single solid-state spin from a spin bath. Science 330, 60–63 (2010).
Leghtas, Z. et al. Confining the state of light to a quantum manifold by engineered two-photon loss. Science 347, 853–857 (2015).
Bretheau, L. et al. Quantum dynamics of an electromagnetic mode that cannot contain N photons. Science 348, 776–779 (2015).
Signoles, A. et al. Confined quantum Zeno dynamics of a watched atomic arrow. Nat. Phys 10, 715–719 (2014).
Barontini, G. et al. Deterministic generation of multiparticle entanglement by quantum Zeno dynamics. Science 349, 1317–1321 (2015).
Schaefer, F. et al. Experimental realization of quantum zeno dynamics. Nat. Commun. 5, 3194 (2014).
Cramer, J. et al. Repeated quantum error correction on a continuously encoded qubit by real-time feedback. Nat. Commun. 7, 11526 (2016).
Bloembergen, N. On the interaction of nuclear spins in a crystalline lattice. Physica 15, 386–426 (1949).
Robledo, L. et al. High-fidelity projective read-out of a solid-state spin quantum register. Nature 477, 574–578 (2011).
Taminiau, T. H. et al. Universal control and error correction in multi-qubit spin registers in diamond. Nat. Nanotechnol. 9, 171–176 (2014).
Waldherr, G. et al. Quantum error correction in a solid-state hybrid spin register. Nature 506, 204–207 (2014).
Dréau, A. et al. Single-shot readout of multiple nuclear spin qubits in diamond under ambient conditions. Phys. Rev. Lett. 110, 060502 (2013).
Jiang, L. et al. Repetitive readout of a single electronic spin via quantum logic with nuclear spin ancillae. Science 326, 267–272 (2009).
Neumann, P. et al. Single-shot readout of a single nuclear spin. Science 329, 542–544 (2010).
Pfaff, W. et al. Demonstration of entanglement-by-measurement of solid-state qubits. Nat. Phys. 9, 29–33 (2013).
Blok, M. S. et al. Towards quantum networks of single spins: analysis of a quantum memory with an optical interface in diamond. Faraday Discuss. 184, 173–182 (2015).
Reiserer, A. A. et al. Robust quantum-network memory using decoherence-protected subspaces of nuclear spins. Phys. Rev. X 6, 021040 (2016).
van Enk, S. J. et al. Experimental procedures for entanglement verification. Phys. Rev. A 75, 052318 (2007).
Massar, S. & Popescu, S. Optimal extraction of information from finite quantum ensembles. Phys. Rev. Lett. 74, 1259–1263 (1995).
Terhal, B. Quantum error correction for quantum memories. Rev. Mod. Phys. 87, 307–346 (2015).
Paz-Silva, G. A. et al. Zeno effect for quantum computation and control. Phys. Rev. Lett. 108, 080501 (2012).
Barreiro, J. T. et al. An open-system quantum simulator with trapped ions. Nature 470, 486–491 (2011).
Zanardi, P. & Campos Venuti, L. Coherent quantum dynamics in steady-state manifold of strongly dissipative systems. Phys. Rev. Lett. 113, 240406 (2014).
Burgarth, J. T. et al. Exponential rise of dynamical complexity in quantum computing through projections. Nat. Commun. 5, 5173 (2014).
Alvarez, G. et al. Zeno and anti-Zeno polarization control of spin ensembles by induced dephasing. Phys. Rev. Lett. 105, 160401 (2010).
Acknowledgements
We thank M. Bakker for experimental assistance and P.C. Humphreys, V.V. Dobrovitski and S.B. van Dam for critically reading the manuscript. We acknowledge support from the Dutch Organization for Fundamental Research on Matter (FOM), the Netherlands Organization for Scientific Research (NWO), and the European Research Council through a Starting Grant. T.H.T. is supported by an NWO VENI grant.
Author information
Authors and Affiliations
Contributions
N.K. and T.H.T. devised the experiment. N.K., J.C. and T.H.T. prepared and characterized the experimental apparatus. D.J.T. and M.M. grew the diamond substrate. N.K. collected and analysed the data with the help of R.H. and T.H.T. N.K. and T.H.T. wrote the manuscript with input from all authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures 1-6, Supplementary Table 1, Supplementary Notes 1-3 and Supplementary References. (PDF 996 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Kalb, N., Cramer, J., Twitchen, D. et al. Experimental creation of quantum Zeno subspaces by repeated multi-spin projections in diamond. Nat Commun 7, 13111 (2016). https://doi.org/10.1038/ncomms13111
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms13111
This article is cited by
-
Robust quantum-network memory based on spin qubits in isotopically engineered diamond
npj Quantum Information (2022)
-
Quantum Zeno effects across a parity-time symmetry breaking transition in atomic momentum space
npj Quantum Information (2021)
-
Tracking the precession of single nuclear spins by weak measurements
Nature (2019)
-
One-second coherence for a single electron spin coupled to a multi-qubit nuclear-spin environment
Nature Communications (2018)
-
Purification of an unpolarized spin ensemble into entangled singlet pairs
Scientific Reports (2017)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.