Abstract
Time-of-flight three-dimensional imaging is an important tool for applications such as object recognition and remote sensing. Conventional time-of-flight three-dimensional imaging systems frequently use a raster scanned laser to measure the range of each pixel in the scene sequentially. Here we show a modified time-of-flight three-dimensional imaging system, which can use compressed sensing techniques to reduce acquisition times, whilst distributing the optical illumination over the full field of view. Our system is based on a single-pixel camera using short-pulsed structured illumination and a high-speed photodiode, and is capable of reconstructing 128 × 128-pixel resolution three-dimensional scenes to an accuracy of ∼3 mm at a range of ∼5 m. Furthermore, by using a compressive sampling strategy, we demonstrate continuous real-time three-dimensional video with a frame-rate up to 12 Hz. The simplicity of the system hardware could enable low-cost three-dimensional imaging devices for precision ranging at wavelengths beyond the visible spectrum.
Similar content being viewed by others
Introduction
Whilst a variety of three-dimensional (3D) imaging technologies are suited for different applications, time-of-flight (TOF) systems have set the benchmark for performance with regards to a combination of accuracy and operating range. TOF imaging is performed by illuminating a scene with a pulsed light source and observing the back-scattered light. Correlating the detection time of the back-scattered light with the time of the illumination pulse allows the distance d to objects within the scene to be estimated by d=tc/2, where t is the TOF and c is the propagation speed of light.
The transverse spatial resolution of the image obtained is retrieved either by using a pixelated array or by using a single-pixel detector with a scanning approach1,2,3,4,5,6,7,8. In both cases, the inherent speed of light demands the use of detectors with a fast response time and high-speed electronic read-out to obtain high precision depth resolution. Advances in sensor development have enabled the first TOF single-photon avalanche detector array cameras to enter the commercial market, having a resolution of 32 × 32 pixels. However, such devices are still in their infancy9,10,11. On the contrary, there are mature single-pixel detectors on the market, which provide stable time-resolved measurements, and by using compressed sensing principles for image reconstruction, which takes advantage of the sparsity in natural scenes, the acquisition times of the scanning approach is largely reduced12,13,14,15,16.
Recently there have been some interesting developments in 3D imaging utilizing single-pixel detectors. One technique utilizes structured illumination and spatially separated photodiodes to obtain multiple images with different shading properties from which 3D images can be reconstructed via photometric stereo17. Another scheme scans a scene, pixel by pixel, using a pulsed illumination source and measures the reflected light using an avalanche photodiode, whereon the first detected photon is used to recover depth and reflectivity via TOF18. An alternative method for scanning a scene and recovering depth and reflectivity via TOF has also been demonstrated utilizing structured pulsed illumination19,20,21,22.
Among the mentioned demonstrations, many5,18,20,21,22 used photon-counting detection (that is, Geiger mode), which is well suited for low-light-level imaging. However, one limitation of photon-counting detectors is the inherent electronic dead time between successive measurements, often 10s of nanoseconds, which prohibits the retrieval of short-range timing information from a single illumination pulse. Instead, an accurate temporal response from a 3D scene requires summing the data over many back-scattered photons and hence many illumination pulses (usually several hundreds or thousands21,22). In contrast, as first demonstrated by Kirmani et al.19, a high-speed photodiode can retrieve the temporal response from a single illumination pulse, which can be advantageous in certain circumstances, for instance when the reflected light intensity is comparatively large. Incidentally, photon counting cannot operate under such conditions since the detection will always be triggered by back-scattered photons from the nearest, or most reflective, object, rendering more distant objects invisible (Supplementary Note 1).
In this paper, we present a single-pixel 3D imaging system using pulsed structured illumination and a high-speed (short response time) photodiode for sampling the time-varying intensity of the back-scattered light from a scene. We show that by using an analogue photodiode to record the full temporal form of the back-scattered light, along with our original 3D reconstruction algorithm, it is possible to recover surface profiles of objects with an accuracy much better than that implied by the finite temporal bandwidth of the detector and digitization electronics. At distances of ∼5 m we demonstrate a range profile accuracy of ∼3 mm with image resolutions of 128 × 128 pixels, whilst simultaneously recovering reflectivity information of the object. This accuracy is achieved despite a detection bandwidth and a digitization interval corresponding to distances of 150 and 60 mm, respectively. We further demonstrate that by using a compressive sampling scheme, the system is capable of performing continuous real-time 3D video with a frame-rate up to 12 Hz.
Results
Experimental set-up
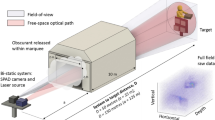
The single-pixel 3D imaging system, illustrated in Fig. 1, consists of a pulsed laser and a digital micromirror device (DMD) to provide time-varying structured illumination. A high-speed photodiode is used in conjunction with a fresnel lens condenser system to measure the back-scattered intensity resulting from each pattern. The analogue photodiode output is passed through a low-noise amplifier and sampled using a high-speed digitizer. In our work we chose to use the Hadamard matrices23 for providing structured illumination. To remove sources of noise, such as fluctuations in ambient light levels, we obtain differential signals by displaying each Hadamard pattern, followed by its inverse pattern, and taking the difference in the measured intensities24,25. Detailed information about experimental set-up is provided in the Methods section.
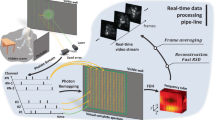
A 3D image of the scene is reconstructed utilizing the time-varying back-scattered intensities (measured for each output pulse of the laser) and the associated set of N patterns used to provide the structured illumination. An overview of the reconstruction algorithm is shown in Fig. 2 (the result in this diagram represents a scene of three objects ∼0.5 m apart in depth). An incident laser pulse (Fig. 2a) is back-scattered from a scene. The high-speed digitizer converts the amplified analogue signals (Fig. 2b) into discrete data points (Fig. 2c), which are subsequently processed by the computer algorithm. Whereas typical single-pixel imaging schemes use the integrated signal for each illumination pattern to reconstruct a two-dimensional image, our algorithm utilizes M discretely sampled intensity points from the time-varying signal to reconstruct M two-dimensional images, resulting in an x, y, z image cube (Fig. 2d). In the image cube, each transverse pixel (x, y) has an intensity distribution (Fig. 2e) along the longitudinal axis (z), which is related to the temporal shape of the pulse, the detector response, the read-out digitization and the pixel depth and reflectivity information.
The incident laser pulses (a) back-scattered from a 3D scene are temporally broadened (b) and discretely sampled using a high-speed digitizer (c). An image cube (d) is obtained using a reconstruction algorithm, having an intensity distribution along the longitudinal axis (e), from which the depth map (f) and the reflectivity (g) of the scene can be estimated.
To enhance the range precision beyond the limits imposed by the sampling rate of the system, methods such as parametric deconvolution19,21 and curve fitting can be used. However, often these methods can be computationally intensive, which makes them unsuitable for real-time applications. Instead we choose to apply cubic spline interpolation to the reconstructed temporal signal at each pixel location, which introduces minimal computational overhead. The depth map of the scene (Fig. 2f) is subsequently determined by finding the maximum in these interpolated signals. In addition, the scene reflectivity (Fig. 2g) can be calculated by averaging the image cube along the longitudinal axis. Utilizing both the depth and reflectivity information, a 3D image of the scene is then reconstructed.
It is worth mentioning that, with the assumption that there is only one surface at each transverse pixel location, our depth estimation (see detail in Methods) works well for scenes that have smooth features, such as the mannequin head and ball, since the reconstructed temporal signals should be slowly varying between sample points. We note that the depth accuracy is limited by the amplitude noise of the data points, over-interpolation only increases the depth precision, but not necessarily the accuracy. In addition, more interpolation adds more processing time, therefore, in our experiments we chose to interpolate by a factor of five times when investigating the static scenes with 20 pulses per pattern (Figs 3, 4, 5), and four times when investigating scenes with motion (Fig. 6), balancing the computational overhead and 3D image quality.
(a) Illustration of the scene containing multiple objects in close proximity. (b) Reflected intensity measured for uniform illumination, indicating temporally indistinguishable objects. (c) The estimated depth map of the scene. (d) The reconstructed scene reflectivity. (e) A textured 3D image of the scene.
The depth estimation (a) reflectivity (b) and 3D reconstruction (c) of a white polystyrene mannequin head at a range of ∼5.5 m. Superposed depth reconstruction and photograph of the mannequin head, viewed from the front (d) and side (e). For a chosen region of interest an error map (f) showing the absolute differences between our depth result and that obtained using a stereophotogrammetric camera system.
(a) Illustration of scene containing a mannequin head with black netting material obscuring the line-of-sight. (b) A photograph of the scene taken from the perspective of the 3D imaging system. The scene depth (c) and reflectivity (d) reconstructed by time-gating the measured intensity data. (e) 3D reconstruction of the mannequin head.
(a) Illustration of the scene containing a static mannequin head and a swinging ball. (b–h) Sample of consecutive depth and reflectivity frames reconstructed at ∼5 Hz frame-rate in real-time for a transverse resolution of 64 × 64 pixels. The experiments of Figs 3, 4, 5, 6 were replicated more than 10 times.
High-resolution imaging
In one experiment, a scene containing a 140-mm diameter polystyrene soccer ball, a life-size skin-tone mannequin head and a screen was located at a distance of ∼5.5 m from the imaging system (Fig. 3a). The objects were closely separated in distance such that the total depth of the scene was ∼360 mm. A complete Hadamard set of 16,384 patterns, and their inverse, was used as the structured illumination, and the back-scattered intensities (Fig. 3b) measured for reconstructing 128 × 128-pixel resolution depth map, reflectivity and 3D image (Fig. 3c-3e). The illumination time of each pattern was 2.66 ms, corresponding to 20 laser pulses. The total time for acquisition, data transfer from the digitizer buffer to the computer and image processing was ∼130 s. The 3D reconstruction shown in Fig. 3e exhibits distinguishable features, such as the profile of the head and the ball.
To quantitatively determine the accuracy of our 3D imaging system, the scene was modified to contain only a polystyrene mannequin head (180 × 270 × 250 mm), for which we had reference 3D data obtained via a high-accuracy stereophotogrammetric camera system17,26. The mannequin head was located at a distance of 5.5 m from the imaging system. To further demonstrate the system capability for retrieving reflectivity in addition to the depth, two grey stripes were placed on the head. Performing the same acquisition and imaging processing used in Fig. 3, we obtained the results shown in Fig. 4a–c. Figure 4d,e show the front and side view comparisons between our 3D reconstruction (green) and photographs of the head (white), respectively. After lateral and angular registration and subsequent depth scaling, an error map representing the absolute differences for a chosen region of interest was obtained (shown in Fig. 4f). From this comparison we find our single-pixel 3D imaging system has a root mean squared error of 2.62 mm. More detailed analysis is provided in Supplementary Fig. 1 and Supplementary Note 2.
Time-gated imaging
One advantage of time-resolved imaging is the ability to distinguish objects at different depths, by artificially time-gating the measured intensity. In certain cases this enables obscuring objects to be isolated from objects of interest. Similar to previous demonstrations20, we constructed a 3D scene containing a polystyrene mannequin head (located at a distance of ∼3.5 m) and black-coloured netting used to obstruct the line of sight (located at a distance of ∼3 m), as illustrated in Fig. 5a. An image of the scene taken using a conventional camera is shown in Fig. 5b, where the head is obscured by the black netting. Performing the same acquisition and imaging processing used in Figs 3 and 4, along with an artificial gating on the photodiode data to ensure no reflected signals from the black netting are included in the 3D reconstruction, we obtained the results shown in Fig. 5c–e. As before, we note the characteristic features of the mannequin head can be resolved.
Real-time compressed video
In addition to obtaining high-quality 3D images of static scenes, many applications demand video frame-rates for motion tracking in dynamic scenes. A key merit of single-pixel imaging is the ability to take advantage of the sparsity of the scene and use compressive sensing to reduce the acquisition time. Most compressive-sensing schemes are performed by minimizing a certain measure of the sparsity, such as L1-norm, to find the sparsest image as the optimal reconstruction of the scene. However, for resolutions greater than 32 × 32 pixels, the time taken by the construction algorithm often prohibits real-time application22,27.
In this work we use an alternative scheme, known as evolutionary compressive sensing6,7, which aims to reconstruct the image with significant less time than conventional compressive sensing by performing a linear iteration (Supplementary Figs 2 and 3 and Supplementary Note 3). In short, the evolutionary compressive sensing scheme chooses a subset of the Hadamard basis to display, by selecting the patterns with the most significant intensities measured in the previous frame, in addition to a fraction of randomly selected patterns that were not displayed. In this experiment, a scene consisting of a static polystyrene mannequin head and a polystyrene white ball (140 mm diameter) swinging along the line of sight with a period of ∼3 s (Fig. 6a). The scene was located at a distance of ∼4 m from the imaging system. Two laser pulses were used per illumination pattern. With the approach described above we obtained continuous real-time 3D video with a frame-rate of 5 Hz using 600 patterns (including their inverse) from the available 64 × 64 Hadamard set, equivalent to a compression ratio of ≃7% (Supplementary Movie 1). The experimental parameters for this result were chosen to balance the inherent trade-off between frame-rate and image quality (Supplementary Note 3). Figure 6b–h show a sample of consecutive frames from the 3D video. The result shows an identifiable 3D image of the mannequin head and ball, in addition to the real-time motion of the ball. Importantly, however, 3D reconstruction can be performed using fewer patterns to achieve higher frame-rates if required, for instance using 256 patterns provides 12 Hz video (Supplementary Movie 2).
Discussion
We have demonstrated that our single-pixel 3D imaging system is capable of reconstructing a scene with millimetric ranging accuracy using modest hardware. In addition, we obtained real-time video rates by taking advantage of a modified compressive sensing scheme that does not rely on lengthy post-processing.
The performance of the system in this work was mainly limited by the repetition rate of the laser used, 7.4 kHz. Using a laser with a repetition rate greater than or equal to the DMD modulation rate, could enable faster 3D video rates by a factor of three and/or increase reconstruction accuracy by increased averaging.
Furthermore, the broad operational spectrum (400–2,500 nm) of the DMD could enable the system to be extended to the non-visible wavelength, such as the infrared, using modified source and detection optics. The use of DMDs in the infrared has already been demonstrated in microscopy6 and real-time video cameras7. The potential application of 3D imaging in the infrared could provide enhanced visibility at long-range, due to reduced atmospheric scattering28.
Methods
Hardware specifications
The following components were used in the experimental set-up (Fig. 1): a pulsed laser (Teem Photonics SNG-03E-100, 532 nm); a DMD (Texas Instruments Discovery 4100 DMD); a projection lens (Nikon ED, f=180 mm); a collection lens (customized fresnel condenser lens, f=20 mm); a Si biased photodiode (Thorlabs DET10A); and a high-speed USB digitizer (PicoScope 6407, 2.5 GS s−1 for two-channel acquisition).
Operating configurations
There are several important points worth mentioning. (a) The modulation rate of the DMD can reach up to 22.7 kHz, however, in this experiment the DMD is operated in slave-mode, meaning the modulation rate is determined by the repetition rate of the laser at 7.4 kHz. (b) The active area of the photodiode is 0.8 mm2, used in conjuction with a 20-mm focal length fresnel lens system, giving a 2.6° field of view, which matches that of the projection system. The depth estimation includes Gaussian smoothing, intensity calibration, cubic spline interpolation and depth determination. More experiment methods and details are provided in Supplementary Methods.
Data availability
The data used to generate all of the figures in this study can be found at http://dx.doi.org/10.5525/gla.researchdata.317.
Additional Information
How to cite this article: Sun, M.-J. et al. Single-pixel three-dimensional imaging with time-based depth resolution. Nat. Commun. 7:12010 doi: 10.1038/ncomms12010 (2016).
References
Schwarz, B. Lidar: mapping the world in 3D. Nat. Photon. 4, 429–430 (2010).
McCarthy, A. et al. Long-range time-of-flight scanning sensor based on high-speed time-correlated single-photon counting. Appl. Opt. 48, 6241–6251 (2009).
Shapiro, J. H. Computational ghost imaging. Phys. Rev. A 78, 061802 (2008).
Bromberg, Y., Katz, O. & Silberberg, Y. Ghost imaging with a single detector. Phys. Rev. A 79, 053840 (2009).
McCarthy, A. et al. Kilometer-range, high resolution depth imaging via 1560 nm wavelength single-photon detection. Opt. Express 21, 8904–8915 (2013).
Radwell, N. et al. Single-pixel infrared and visible microscope. Optica 1, 285–289 (2014).
Edgar, M. P. et al. Simultaneous real-time visible and infrared video with single-pixel detectors. Sci. Rep. 5, 10669 (2015).
Sun, M.-J., Edgar, M. P., Phillips, D. B., Gibson, G. M. & Padgett, M. J. Improving the signal-to-noise ratio of single-pixel imaging using digital microscanning. Opt. Express 24, 260309 (2016).
Niclass, C. & Charbon, E. in Solid-State Circuits Conference. Digest of Technical Papers 364–604 (San Francisco, CA, USA, 2005).
Richardson, J. et al. in Custom Integrated Circuits Conference, 77–80 (San Jose, CA, USA, 2009).
Entwistle, M. et al. in Proc. SPIE, (ed. Itzler, M.A.) Vol. 8375 (SPIE, 2012).
Baraniuk, R. G. Compressive sensing [lecture notes]. IEEE Signal Process. Mag. 24, 118–121 (2007).
Duarte, M. F. et al. Single-pixel imaging via compressive sampling. IEEE Signal Process. Mag. 25, 83–91 (2008).
Young, M. et al. Real-time high-speed volumetric imaging using compressive sampling optical coherence tomography. Biomed. Opt. Express 2, 2690–2697 (2011).
Hatef, M., Sina, J., Matan, G. & Donoho, D. L. Deterministic matrices matching the compressed sensing phase transitions of gaussian random matrices. Proc. Natl Acad. Sci. USA 110, 1181–1186 (2013).
Herman, A. M. A., Tidman, J., Hewitt, D., Weston, T. & Mcmackin, L. in Proc. SPIE (ed. Fauzia Ahmad) Vol. 8717 (SPIE, 2013).
Sun, B. et al. 3D computational imaging with single-pixel detectors. Science 340, 844–847 (2013).
Kirmani, A. et al. First-photon imaging. Science 343, 58–61 (2014).
Kirmani, A., Colaço, A., Wong, F. N. & Goyal, V. K. Exploiting sparsity in time-of-flight range acquisition using a single time-resolved sensor. Opt. Express 19, 21485–21507 (2011).
Howland, G. A., Dixon, P. B. & Howell, J. C. Photon-counting compressive sensing laser radar for 3D imaging. Appl. Opt. 50, 5917–5920 (2011).
Colaco, A., Kirmani, A., Howland, G. A., Howell, J. C. & Goyal, V. K. in Proceedings of the 2012 IEEE Conference on Computer Vision Pattern Recognition (CVPR) 96–102 (Washington, DC, USA, 2012).
Howland, G. A., Lum, D. J., Ware, M. R. & Howell, J. C. Photon counting compressive depth mapping. Opt. Express 21, 23822–23837 (2013).
Pratt, W. K., Kane, J. & Andrews, H. C. Hadamard transform image coding. Proc. IEEE 57, 58–68 (1969).
Sun, B. et al. in Computational Optical Sensing and Imaging OSA, CTu1C–4 (2013).
Sun, M.-J., Li, M.-F. & Wu, L.-A. Nonlocal imaging of a reflective object using positive and negative correlations. Appl. Opt. 54, 7494–7499 (2015).
Khambay, B. et al. Validation and reproducibility of a high-resolution three-dimensional facial imaging system. Br. J. Oral Maxillofac. Surg. 46, 27 (2008).
Aβmann, M. & Bayer, M. Compressive adaptive computational ghost imaging. Sci. Rep. 3, 1545 (2013).
Bucholtz, A. Rayleigh-scattering calculations for the terrestrial atmosphere. Appl. Opt. 34, 2765–2773 (1995).
Acknowledgements
We thank Prof. Adrian Bowman and Dr Liberty Vittert for providing the stereophotogrammetric 3D data of the polystyrene mannequin head. M.S. acknowledges the support from National Natural Foundation of China (Grant No. 61307021) and China Scholarship Council (Grant No. 201306025016). M.J.P. acknowledges financial support from UK Quantum Technology Hub in Quantum Enhanced Imaging (Grant No. EP/M01326X/1), the Wolfson foundation and the Royal Society.
Author information
Authors and Affiliations
Contributions
M.-J.S., R.L. and M.J.P. conceived the concept of the experiment; M.-J.S., M.P.E. and G.M.G. designed and performed the experiments; M.-J.S., M.P.E. and M.J.P. designed the reconstruction algorithm; N.R. developed the evolutionary compressed sensing algorithm; M.-J.S., M.P.E., B.S. and M.J.P. analysed the results; M.-J.S., M.P.E. and M.J.P. wrote the manuscript and other authors provided editorial input.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures 1-3, Supplementary Notes 1-3, Supplementary Methods and Supplementary References. (PDF 2091 kb)
Supplementary Movie 1
Real-time three-dimensional video of a mannequin head and a swinging ball. (MOV 3301 kb)
Supplementary Movie 2
Real-time three-dimensional video of a swinging ball. (MOV 2348 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Sun, MJ., Edgar, M., Gibson, G. et al. Single-pixel three-dimensional imaging with time-based depth resolution. Nat Commun 7, 12010 (2016). https://doi.org/10.1038/ncomms12010
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms12010
This article is cited by
-
A compressive hyperspectral video imaging system using a single-pixel detector
Nature Communications (2024)
-
Efficient single-pixel imaging based on a compact fiber laser array and untrained neural network
Frontiers of Optoelectronics (2024)
-
Massively parallel electro-optic sampling of space-encoded optical pulses for ultrafast multi-dimensional imaging
Light: Science & Applications (2023)
-
Mid-infrared single-pixel imaging at the single-photon level
Nature Communications (2023)
-
Deep Memory-Augmented Proximal Unrolling Network for Compressive Sensing
International Journal of Computer Vision (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.