Introduction

There has been extensive theoretical study on the extent to which selection and mutation can preserve genetic variation in quantitative characters (see reviews by Bulmer, 1985 and Roff, 1997a). In a finite population, genetic variation can be maintained by a balance between stabilizing selection and mutation (Bürger et al., 1989; Houle, 1989; Foley, 1992; Bürger & Lande, 1994), but directional selection leads to a rapid depletion of genetic variance because of fixation (Bulmer, 1976, 1985). This latter prediction applies only to traits in which the quantitative variation is expressed at the phenotypic level (Roff, 1994a). There is a large class of traits which are expressed as two or a few discrete phenotypes (Wright, 1968; Falconer, 1989; Roff, 1996); examples include cyclomorphosis, paedomorphosis and paedogenesis, ‘weaponry’ (enlarged mandibles, cerci, head structures, etc.) in insects, trophic dimorphisms in amphibians and fish, wing dimorphism in insects, diapause, modes of reproduction (semelparity vs. iteroparity), and mating behaviours (e.g. satellites vs. territorial males: for a review see Roff, 1996). Although these traits are phenotypically discrete, their inheritance may be polygenic, the particular manifestation of the trait being a function of a threshold of sensitivity (Falconer, 1989; Roff, 1996). According to the threshold model, a continuously varying character underlies the expression of the trait, individuals with values lying above the threshold being of one type, whereas individuals lying below the threshold are the other. The underlying trait, termed the liability, is assumed to be inherited in the usual polygenic manner.

Directional selection on a threshold trait occurs when the frequency of one morph has a greater representation in the parent pool than in the population as a whole. In the extreme case only individuals of one morph contribute to the next generation. Unlike directional selection on a trait displaying continuous phenotypic variation, the selection intensity accompanying directional selection on a threshold trait decreases with each generation. Suppose, for example, the population originally comprises 50 per cent of each morph and only one morph is selected as parents for the following generation. In the first generation of selection 50 per cent of the population will be selected, but the second generation consists of greater than 50 per cent of the selected morph, and hence the selection intensity on the second generation must be less than on the first. As the proportion of the selected morph increases in frequency the intensity of selection declines. The consequence of this is that the rate of erosion of genetic variation is very slow (Roff, 1994a, 1996). Such slow rates of erosion may partly explain the presence of considerable genetic variance for dimorphic traits (see Roff, 1996 table 1: the mean heritability of the 18 estimates is 0.52). Most of the dimorphic traits studied are closely connected to fitness (diapause propensity, wing dimorphism, sex ratio) and hence are likely to be under strong selection.

Table 1 Values of p, VA and h2 predicted assuming an infinite population size (N=∞) and observed for a population size of 5000
Full size table

The hypothesis investigated in this study is that genetic variance is eroded sufficiently slowly that losses are replaced by mutation. This hypothesis is examined via simulation modelling, with detailed analysis being given to the two selection extremes, that in which only a single morph contributes to the next generation and that in which there is no selection. A theoretical analysis is also presented, based on the assumption that population size is sufficiently large that genetic drift can be ignored.

Description of the simulation model

The simulation model is similar to that used by Bulmer (1976) in his analysis of directional selection on a quantitative trait and that of my previous analysis of directional selection on a threshold trait in the absence of mutation (Roff, 1994a). The underlying, continuously distributed character (liability) was assumed to be determined by n (=10 or 50) unlinked loci, each with two alleles contributing either 0 or 1 to the phenotypic value. The initial distribution of allelic values was obtained by randomly assigning 0 or 1, thereby giving an average per locus frequency of 0.5. I assumed no dominance or epistasis. The additive genetic variance, assuming Hardy–Weinberg equilibrium and linkage equilibrium in the unselected population, was thus equal to 0.5n. The phenotypic value of an individual was obtained as the summed contribution of all loci plus a random normal deviate distributed with zero mean and variance VE. The environmental variance, VE, was determined from the heritability in the unselected population and the relationship h2=VA/ (VA+VE), where h2 was set to 0.5 to correspond to the average value observed for threshold traits (see Introduction). In the founding population both morphs were set at equal frequency, obtained by setting the threshold value equal to n. Each generation consisted initially of N individuals (N=25, 50, 100, 250, 500, 2000, 5000). Directional selection was applied by the use of a selection coefficient s: the probability of individuals above the threshold contributing was set at 1−s and those below the threshold at 1. Thus when s=0 there is no selection, and when s=1 only individuals with phenotypic values less than the threshold value are selected. Intermediate values of selection intensity were obtained by generating for each individual lying above the threshold a random number; if this number was greater than s then the individual contributed to the next generation. To generate the next generation, N pairs were chosen with replacement from the selected population to form the parents of the next generation, each pair contributing one offspring. Each allele in the offspring had the same probability, μ (=10−4, 10−5), of mutating to the alternate allele.

Analysis of simulations

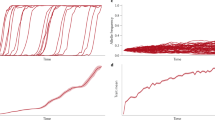
In the first series of simulations the selection coefficient was set at either 0 or 1. Inspection of time traces showed considerable variation in additive genetic variance over time (Fig. 1). The two sample runs shown in Fig. 1 illustrate the general finding that equilibrium genetic variance is achieved after ≈2500 generations, and that several thousand generations must be averaged to obtain an adequate estimate of the long-term equilibrium value. Depending on population size and number of loci the simulation was run for either 10,000 generations (for all runs without selection, and with selection for runs with combinations n=50, all N; n=10, N=5000) or 50,000 generations (n=10, N<5000). In the former case the parameters were estimated by averaging the last 2000 generations, and in the latter case by averaging over the last 10,000 generations. Comparison of results obtained over both the short and long time intervals showed that the former are adequate (Fig. 1). Each run was replicated either five (without selection, combinations of n=10, μ=both, N=2000, 5000; n=50, μ=both, N=all: with selection, all combinations with n=50) or 20 (without selection, combinations of n=10, both μ, N<2000: with selection, all combinations with n=10) times.

Fig. 1
figure 1

Mean genetic variance calculated over intervals of 250 generations for two simulation runs of 50,000 generations. In both cases μ=10−5. Note that the y-axis is on a log scale.

Full size image

Under directional selection (s=1) the additive genetic variance and heritability increase with population size, with an approximate asymptote being reached at a population size of 5000, except for the combination μ=10−5, n=50 in which it is apparent that VA and h2 are still increasing beyond N=5000 (Fig. 2). Similarly, the mean allele frequency increases to an asymptote (except in the aforementioned combination), while the percentage of the morph selected against declines, although the total number of this morph increases (Fig. 3). The percentage of the selected morph that remains at equilibrium is extremely low (<2 per cent) and considerably less than is frequently observed in dimorphic populations.

Fig. 2
figure 2

Effects of selection, number of loci and population size on additive genetic variance and heritability. Open symbols show results from simulations with no selection, closed symbols show results from simulations with directional selection. Triangles, μ=10−4; circles, μ=10−5.

Full size image
Fig. 3
figure 3

Effects of selection, number of loci and population size on allelic frequency, proportion of morph selected against, and number of this morph. Open symbols show results from simulations with no selection, closed symbols show results from simulations with directional selection. Triangles, μ=10−4; circles, μ=10−5.

Full size image

At small population sizes there will be considerable variation between loci in their allelic frequencies, with some loci being fixed at any particular generation (mutation will restore variability to these loci whereas the combined effects of drift and selection will fix others). As population size increases the proportion of loci fixed at any given time will decrease, thereby increasing genetic variance. At an infinite population size all loci will have the same allelic frequency, p, and the additive genetic variance should then be equal to 2np(1−p). The ratio of 2n ¯p (1−¯p), where ¯p is the mean allele frequency from the simulation, to the observed mean additive genetic variance declines steadily with population size and is close to 1 at N=5000 for three of the combinations (μ=10−4, n=10, ratio=1.05; μ=10−4, n=50, ratio=1.13; μ=10−5, n=10, ratio=1.08) but has only declined to 1.82 for μ=10−5, n=50 (Fig. 4). These results are consistent with the asymptotic behaviour of the four combinations (Fig. 2).

Fig. 4
figure 4

Plot of the ratio, 2n ¯p (1−¯p)/observed mean additive genetic variance, where ¯p is the mean allele frequency from the simulation, as a function of population size, at two different mutation rates.

Full size image

In the absence of selection, VA and h2 do not differ greatly from those observed with selection except when the number of loci is small (n=10) and population size moderate to large (N>250, Fig. 2). However, although genetic variance with or without selection may be approximately the same, the mean allelic frequencies differ substantially (Fig. 3). Without selection, allelic frequencies fluctuate about 0.5, whereas with selection they are never below 0.6 and increase with population size. The equilibrium percentage of the two morphs varies between 33 per cent and 84 per cent with an overall mean of 51 per cent, as would be expected in the absence of selection. There is no relationship with population size (this also is to be expected, although the variance among generations should decrease with increasing population size). Thus directional selection is effective at shifting allele and morph frequencies but population size and number of loci are the most significant determinants of genetic variance.

At the higher population sizes, a considerable fraction of the initial heritability is preserved; for example, with n=50, μ=10−4 and N=5000, the equilibrium heritability is 82 per cent (h2=0.41) of its original value. Decreasing the number of loci or the mutation rate decreases the equilibrium heritability (e.g. for the foregoing example, h2=0.21 when n=10, and h2=0.29 when μ=10−5). With respect to the hypothesis advanced in the Introduction, the simulation results show that for moderate to large population sizes a significant portion of the original additive genetic variance can be maintained by a balance between selection and mutation. However, little phenotypic variability is maintained (< 2 per cent of the selected morph).

The above analysis assumes that only a single morph contributes to the following generation (s=1); more generally, 0<s<1. Even with s<1 there will still be directional selection favouring the alternate morph and hence a priori we expect the equilibrium values to be robust to the value of s. This hypothesis was confirmed by running the simulation model for varying values of s: for s>0.2 there is little change in parameter values (Fig. 5). Heritabilities and additive genetic variances vary only by twofold between complete selection (s=0) and no selection (s=1, see also Fig. 2). Furthermore, the equilibrium percentage of the selected morph is generally below 2 per cent, as found for the case of complete selection (lower right panel, Fig. 5). With s as low as 0.02 the equilibrium percentage of the selected morphs is only 1.7 per cent (μ=10−5, n=10, N=500) and 6.6 per cent (μ=10−5, n=50, N=500, Fig. 5).

Fig. 5
figure 5

Effect of varying the selection coefficient, s, on the equilibrium genetic parameters for a population size of 500 with mutation rates of 10−4 (triangles) and 10−5 (circles). Values in the former case are the means of 20 replicates, and in the latter case they are the means of five replicates for each value of s.

Full size image

A theoretical analysis

As noted above, for an infinite population, where there is no genetic drift, all loci will have the same allelic frequency, p; therefore, the selection intensity will be the same at all loci and we can apply standard single-locus theory (Crow & Kimura, 1970, p. 258). Considering a single focal locus, the contributions to the phenotypic value of the three possible genotypes, labelled AA, Aa and aa, are 2, 1 and 0, respectively. Assuming, without loss of generality, that selection operates against the morph produced by phenotypic values exceeding the threshold, then the probability that a particular genotype is subject to selection is equal to the probability that the addition of this genotypic value to the cumulative value of all other loci plus the environmental value produces a phenotypic value that is greater than the threshold value, T (=n in the present simulations; analysis of the theoretical model shows that the results are quite robust to T). The phenotypic value set by the n−1 ‘nonfocal’ loci and the environmental effect is distributed as a random normal variable with mean μ=2(n−1)p and variance σ2=2(n−1)p(1−p)+VE, where VE is determined as described in the section ‘Description of the simulation model’. The fitness of genotype AA, WAA, is thus: . The relative fitnesses of Aa and aa, (WAa, Waa, respectively) are calculated in the same manner, replacing T−2 with T−1 and T, respectively. At equilibrium we have (Crow & Kimura, 1970, p. 259, eqn 6.22): which can be solved numerically. With a mutation rate of 10−4 the predicted equilibrium values of p are very similar to those obtained from the simulation with N=5000, but there are significant differences between observed and predicted genetic variances and heritabilities for μ=10−5 (Table 1). The predicted heritability at n=10 and μ=10−5 is larger than that observed but this may result from estimation errors in p (a change in the second decimal place alters h2 by 30 per cent). The discrepancy for n=50, μ=10−5 is in accord with the observation from the simulation model that VA shows no asymptote at a population size of 5000 (Fig. 2); it is possible that the difference for n=10 also reflects a slow approach to an asymptote.

The additive genetic variance and heritability increase as selection against a particular morph decreases (s approaches 0) but, as hypothesized and found with the simulation model, the greatest change occurs only when s is less than 0.2 (Fig. 6). When the differences in fitness are very small (s<0.01), the equilibrium heritabilities are quite large (h2=0.32 for n=10 and h2=0.46 when n=50). However, if, as is likely, the number of loci is at least 50 the heritability when s equals 0 is already so large (0.42) that the increase in h2 is relatively small (9.5 per cent). The equilibrium proportion of the selected morph is much more sensitive to s at the lower extreme: whereas the equilibrium percentage when there is no selection is 50 per cent, the equilibrium percentage when s is increased from 0 to 0.01 declines to less than 0.5 per cent (0.41 per cent for n=10 and 0.36 per cent for N=50; lower right panel, Fig. 6). Thus, even if a particular morph has a relative probability of contributing to the next generation of 0.99, selection will still drive this phenotype down to a very low representation in the population. It is only when s is less than 10−4 that the equilibrium proportion of the selected morph increases above 20 per cent (see inset in Fig. 6). The preservation of significant proportions of both morphs in the population requires that the selection intensity be very weak.

Fig. 6
figure 6

Effect of varying the selection coefficient, s, on the equilibrium genetic parameters for n=10 (solid line) and n=50 (dashed line). Values calculated using the theoretical model assuming a mutation rate of 10−5.

Full size image

Conclusions

Effective population sizes in excess of 5000 are probably not uncommon, particularly for invertebrate species. In such cases, genetic variation for dimorphic traits could be preserved even though selection continually favours one morph. However, as intuitively expected and shown by the simulation model, unless selection is very weak (s<0.001), the phenotypic variation will be very low, less than 2 per cent of the population displaying the phenotype of the morph being selected against (Figs 3 and 6). The ratio of morphs is typically much higher than this; in fact, populations with such low frequencies would generally be termed monomorphic. Thus the present results show that the phenotypic variation observed in nature is not a consequence of a simple balance between directional selection and mutation. The important message is that much of the genetic variation in large populations is shielded from selection and hence the questions of what maintains genetic variation vs. what maintains phenotypic variation might have fundamentally different answers. Phenotypic variation in threshold traits is likely to be largely a function of frequency-dependent selection or a result of phenotypic plasticity (induction of protective structures in the presence of a predator cue; Roff, 1994b, 1996). This type of selection can readily preserve phenotypic variation and can play an important role in the preservation of genetic variation in quantitative traits (Mani et al., 1990; Roff, 1997a). Its importance in maintaining genetic variation in threshold traits is explored elsewhere (Roff, 1997b).

Many populations may be small and isolated with effective sizes in the tens or hundreds rather than thousands. For such populations the present analysis shows that genetic drift is likely to play a dominant role. The importance of drift also increases with the number of loci. The reason for this is discernible from the above theoretical model: as the number of loci increases, the per locus selection coefficient decreases because the likelihood that a particular locus will move a genotype over the threshold value decreases.

In conclusion, large amounts of additive genetic variance can be maintained in a threshold trait, even in the face of directional selection, provided that population size and/or the number of loci is large. However, other factors must be important in maintaining the phenotypic variation. A likely candidate is frequency-dependent selection, investigation of which is described in Roff (1997b).