Introduction

As is well known, quantum entanglement1 is a vital resource in quantum information processing (QIP) tasks, such as quantum teleportation2, quantum dense coding3, quantum remote preparation4,5,6, quantum cryptography7 and so on. Therefore, it has attracted a lot of attention. As a matter of fact, typical discussions of entanglement have been built on nonlocality, Bell inequality violations, monotones over local operations and classical communication, etc. For example, entanglement was discussed in many previous literatures focused on time reversal, local uncertainty relations8, entanglement witnesses9,10, entropic uncertainty relations11,12, concurrence13 and the covariance matrix criterion14. However, it is important to note that some states with zero entanglement can perform some tasks which are not possible in a classical regime. The conventional entangled-separate state framework seems to be inappropriate in the sense of characterizing and quantifying quantum correlations. Quantum correlation is more general and more fundamental than entanglement, which offers a more useful non-classical resource. Actually, the system is generally open and avoidably interacts with its surrounding environment15,16,17,18,19, resulting in a loss of quantum coherence, which in turn destroys the quantum correlations. Recently, the dynamics of quantum and classical correlations under both Markovian and non-Markovian decoherence have extensively observed20,21,22,23. Interestingly, contrary to the case of entanglement dynamics where sudden death might occur24,25,26, quantum correlation does not exhibit such a behavior.

Quantum physics differs significantly from classical physics in many aspects. A complete classical description of an object contains information concerning only compatible properties, while a complete quantum description of an object contains complementary information concerning incompatible properties. This difference also appears in correlations. Recently, Lorenzo Maccone et al.27 defined the complementary correlations, and entanglement detection based on which is capable of detection of a variety of entangled states that entanglement witnesses miss. And Wu et al.28 revealed that for a bipartite quantum state, the classical correlation is the maximal correlation based on a certain optimal basis, while the quantum correlation is characterized as a series of residual correlations in the mutually unbiased bases. Furthermore, Prasenjit Deb et al.29 optimized the previous outcomes. They explained what the underlying physical mechanisms are for classical and quantum correlations (measured in terms of discord) suffering sudden change in the decoherence process. The above paper, however, has used two complementary observables. It is well known that all systems have at least three complementary observables and there are d + 1 for d-dimensional systems if d is a power of a prime30. Motivated by this, our work is readily to extend to a general case of three complementary observables.

To begin with, we review different measures of complementary correlations, and then state our results. The detail proofs of the results are rendered in the part of Methods.

Results

Complementary correlations

Complementary correlaitions, introduced by Lorenzo Maccone et al.27, can reveal the genuine quantum correlations present in a composite quantum system. If the classical correlation is the maximal correlation based on a certain optimal basis, the quantum correlation is characterized as a series of residual correlations on the mutually unbiased bases. In other words, we can not only obtain classical correlation, but also can obtain the quantum correlation by residual correlations on the mutually unbiased bases.

Considering a quantum system with finite dimension d, let M and N be two observables acting on the system, with |mi〉 and |ni〉 denoting the non-degenerate eigenstates. If we have for all i, j, where d is the dimension of Hilbert space, M and N are two complementary observables, respectively. According to the Supplement Material of ref. 27, for a bipartite system in a Hilbert space H1 ⊗ H2, there are three observable A ⊗ B, C ⊗ D and E ⊗ F (see Fig. 1), where A, C and E are complementary observables in the first system, B, D and F in the second. Then the quantity |χAB| + |χCD| + |χEF| denotes the value of the complementary correlations, where |χXY| denotes the absolute values of the correlations for complementary observables and can be quantified by any one of the three possibilities: Pearson correlation coefficient, mutual information and sum of conditional probabilities. In this paper, we special focus on Pearson correlation coefficient and mutual information.

Figure 1: Complementary correlation measurements.
figure 1

System 1 and System 2 are the subsystems of the composite system. A, C and E are the complementary observables for system1 and B, D and F are the complementary observables for system 2.

Full size image

Pearson correlation

The Pearson correlation coefficient CXY is defined as

where X and Y denote observables relative to the two systems, 〈M〉 = Tr[Mρ] is the expectation value for the quantum state ρ and is the variance of the observable M. It is worth noting that the eigenstates of X or Y cannot apply to above quantity. The complementary correlation reads as CAB + CCD + CEF. For the correlation, one can obtain the following results27:

  1. a

    CXY = 0 for uncorrelated (product) states.

  2. b

    If a state is maximally entangled if and only if there exist three complementary bases of linear observables such that CAB + CCD + CEF = 3.

  3. c

    If CAB + CCD + CEF > 1, the two systems are entangled. It gives a sufficient condition for entanglement that can be used for entanglement detection.

  4. d

    The separable states fulfill the condition CAB + CCD + CEF ≤ 1.

Mutual information

The mutual information I is defined by

where H (A) = Σap(a) log2(p(a)) is the Shannon entropy of the measurement A performed on the first system, where p(a) is the probability of outcome a, and H (A/B) is the conditional entropy conditioning on the second system, which can be written as H (A/B) = Σap(b)H (A/B = b), where H (A/B = b) = −Σap(a/b) log2 p(a/b) is the entropy of the probability distribution p(a/b) for fixed outcome b. Therefore, in terms of mutual information, the complementary correlation reads as IAB + ICD + IEF. It can be easily shown that:

  1. a

    The state of a bipartite quantum system is maximally entangled, if and only if there exist three complementary measurement bases, where IAB + ICD + IEF = 3log d.

  2. b

    If IAB + ICD + IEF > log d, the state of the bipartite system is entangled.

  3. c

    The separable states fulfill the condition IAB + ICD + IEF ≤ log d.

Identification of entangled Bell diagonal states

The density operator of two-qubit Bell diagonal states has the form

where IA(B) is an identity matrix, σi denote Pauli matrices and ci are spin-spin correlation functions. In matrix notation, we explicitly have

In this paper, we choose three suitable complementary observables, σ1, σ2, σ3 forming a set of complementary observables, which are used for a qubit and A = B = σ1, C = D = σ2, E = F = σ3. According to Eqs (1, 2 and 4), the classical correlations for complementary properties can be obtain as

and

With respect to the four Bell states (|c1| = |c2| = |c3| = 1), it satisfies the conditions CAB + CCD + CEF = 3. As to Werner states , (|c1| = |c2| = |c3| = r), the state parameter r ∈ [0, 1], according to Eq. (4) and criterion (c1), it can be obtained that when , the system is entangled. Besides, we plot the Bell diagonal states as a function of c1, c2, and c3 in Fig. 2. From the figure, all Bell diagonal states lie in the tetrahedron I, with four vertices situate on the points of (1, 1, −1), (1, −1, 1), (−1, 1, 1), and (−1, −1, −1) being four Bell states (CAB + CCD + CEF = 3). When CAB + CCD + CEF > 1, there are four entangled regions that can be used as entanglement identification outside of red region. If the state is separable, it will surely satisfy CAB + CCD + CEF ≤ 1, it is inside of red region. The red plane CAB + CCD + CEF = 1 can be used as the entanglement threshold of Bell diagonal states. Compared with Concurrence, which is a measure of entanglement, Pearson correlation can be used to identify all two-qubit entangled Bell diagonal states. In the part of Methods, we present the strict numerical proof.

Figure 2: Geometrical representation of Bell-diagonal states.
figure 2

All Bell diagonal states lie in the tetrahedron I. Separable states are inside of octahedron (red region).

Full size image

The dynamic behavior of complementary correlation under the decoherence channels

Now, we will explore the influences of decoherence channels on the Bell diagonal states, when the states are coupled with local decoherence channels. In this context, we consider the system-environment interaction through the operator-sum representation formalism. Following the Kraus operators approach, the time-evolved state under local noisy environment can be described by the trace-preserving quantum operation, which is

where Ki,j is Kraus operator corresponding decoherence channel, satisfying the trace-preserving condition . For the sake of simplicity, we provide a list of Kraus operators for a variety of channels considered in Table 1, where p is the time dependent parameter. As a matter of convenience, the dynamics evolutions of correlations with the time for the two-qubit states can be substituted by those with the parameter p. Decoherence processes (bit flip, phase flip and bit phase flip) preserve the Bell-diagonal form of the density operator ρ. In this situation, we can write the quantum operation ε(ρ) as

Table 1 The Kraus operators for the quantum channels: bit flip, phase flip, and bit-phase flip channels.
Full size table

where is shown in Table 2. Similarly, we can also give the entanglement critical condition that can be used for entanglement identification under decoherence channels by the threshold . When p < p*, the entanglement is non-zero, vice versa, where p* is the entanglement critical value in Table 3.

Table 2 Correlation functions for the quantum operations: bit flip, phase flip and bit-phase flip channels.
Full size table
Table 3 The entanglement critical value under the decoherence channels.
Full size table

Here we take two-qubit Bell diagonal states under the bit flip as an example to illustrate why entanglement suffers a sudden death.

The bit flip channel signifies that it flips both the bit and the phase of a qubit. The evolution of a density matrix ρ for it is given by

If one considers a single-qubit pure state ψ, then the evolution of the state for the bit-phase flip channel can be given by the mapping |ψ〉 → σ2|ψ〉.

According to Eqs (1) and (8), the Pearson correlation coefficients can be obtain as , and . From the numeral calculation, we can see that and are degenerated, because of the effect of noisy channel. When , the entanglement undergoes a sudden death. In other words, entanglement degeneration is shown in the degeneration of and . It can give us a new idea to protect entanglement by attempting protection of and .

Sudden Transition between Classical and Quantum Correlation in the decoherence process

Sudden transition between classical and quantum correlation has been studied within several literatures19,21,22. In this paper, we will give a new interpretation based on complementary correlations.

We proceed by investigating the sudden transition of correlations using the Bell diagonal states. Furthermore, we consider the initial states as c1 = 1 and , with c3 < 1. From the definition of Pearson correlation coefficient and mutual information, we have

and

and the total complementary correlations are

and

According to ref. 31, the classical correlation and quantum correlation, measured by geometric quantifiers, for Bell-diagonal states, are given by and , respectively, where describes the intermediate result among the absolute values of the correlation functions , , and . The classical correlation (J) and quantum correlation (QD)21, measured based on entropy, can be obtained

and

where and . With Eqs (10) and (11), we find that

and

From above, they show that complementary correlation not only reveals the behavior of classical correlation, but also show the behavior of quantum correlation.

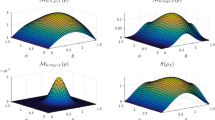
To address the question about sudden transition between classical and quantum correlation under local decoherence channels, we focus on exploring dynamical behavior of quantum correlations under phase flip channel. Conveniently, we depict the behavior of Pearson correlation coefficient, geometric classical correlation, geometric quantum discord with the parameter p for c1 = 1 and c2 = −c3 = −0.6 in Fig. 3 and the behavior of mutual information, classical correlation and quantum discord in Fig. 4. These plots clearly display the sharp transition from classical to quantum correlation occurring at p = psc in decoherence regime. When 0 < p < psc, the classical correlations decay and the quantum correlations remain constant. In other words, we can say that the correlations and decay, the correlations and remain constant. When p > psc, the classical correlation is constant, whereas the quantum correlation starts to decay. Analyzing physical origin of the sudden transition, we consider that when 0 < p < psc, the projective measurement on the eigenstates of observables σ1 will yield the classical correlations, the quantum correlation is characterized in the eigenstates of observables σ3. Corresponding, when p > psc the projective measurement on the eigenstates of observables σ3 will yield the classical correlations, the quantum correlation is characterized in the eigenstates of observables σ1. Meanwhile, we notice that correlation is constant under this processing, its physical source is that the phase flip channel induces a decay in the quantum coherence of the state ε(ρ), which results in a decay in the expectation of σ1 ⊗ σ1, whereas the expectation value of σ3 ⊗ σ3 remains constant. If we consider, instead of bit flip noise, the bit-phase flip channel, then the coefficients change as Table 2. It is very easy to exhibit the same sudden transition in their evolution. Moreover, such sudden transitions can also be explained through complementary correlations.

Figure 3
figure 3

Sudden change behavior for the state given by c1 = 1 and c2 = −c3 = −0.6 under the phase flip channel.

Full size image
Figure 4
figure 4

Sudden change behavior for the state given by c1 = 1 and c2 = −c3 = −0.6 under the phase flip channel.

Full size image

Conclusions

To summarize, we explore an effective method to identify the entangled Bell diagonal states by means of Pearson correlation, one of the complementary correlations. Furthermore, the dynamic behavior of complementary correlations under various kinds of decoherence channels are exposed. A new interpretation of sudden death and revival of entanglement in terms of Pearson correlation is proposed. The entanglement threshold p* being used to identify entanglement is revealed. Meanwhile, we find that the dynamic behavior of classical correlations for complementary properties is a good interpretation in quantum correlation problem. If the classical correlation is the maximal correlation on a certain optimum basis, the quantum correlation will be characterized as a series of residual correlations on the mutual unbiased bases. In other words, the sudden transition behaviors reveal not only classical but also quantum correlations in terms of complementary correlations. Therefore, we believe our investigation might bring some new attempts to study protection of entanglement and provide a nice insight into interpreting sudden transition behavior of classical and quantum correlations in the decoherence process.

Methods

Entangled Bell diagonal states

The entanglement of Bell-diagonal states coupled with the noisy environments can be quantified conveniently by concurrence25, E = max{0, 2 max λi − 1}, where λi is the eigenvalue of Bell-diagonal states. We can obtain that the state is entangled when .

Geometric correlations

Geometric quantifiers of quantum (namely, GQD-1) and classical correlations between A and B can be defined through the trace distances31, QG = inf tr|ρ − χ| = tr|ρ − χρ| and CG(ρ) = tr|χρ − πρ|, where χρ is a classical-quantum state and πρ represents the product of the local marginals of ρ.

Classical correlation and quantum discord

The classical correlations of a composite quantum state can be quantified via the measure proposed by Henderson and Vedral32 which is given by , where the maximum is taken over the set of projective measurements {∏j} on subsystem B. is the entropy of subsystem A conditioned on B, is the density matrix of subsystem A depending on the measurement outcome for B, and is the probability of the jth outcome.

The quantum discord, which is a measure of quantum correlation, is defined as QD(ρAB) = I(ρAB) − J(ρAB), where I(ρAB) = S(ρA) + S(ρB) − S(ρAB) is the quantum mutual information.

Additional Information

How to cite this article: Du, M.-M. et al. The dynamical behaviors of complementary correlations under decoherence channels. Sci. Rep. 7, 40934; doi: 10.1038/srep40934 (2017).

Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.