Introduction

Exact solutions for mixed or free convection flow of viscous fluid problems are abundance in literature. However, such solutions for non-Newtonian fluids are rare, particularly for Maxwell fluids, such solutions do not exist. Generally, in non-Newtonian fluids, the relation which connects shear stress and shear rate is non-linear and the constitutive relation forms equations of non-Newtonian fluids which are higher order and complex as compared to Navier-Stokes equation governing the flow of viscous fluid. Due to this high nonlinearity, closed form solutions for non-Newtonian fluid flows are not possible for the problems with practical interest. More exactly, when such fluids problems are tackled via Laplace transform technique, often the inverse Laplace transforms of the transformed functions do not exist. Due to this difficulty, the researchers are usually using numerical procedures for finding the inverse Laplace transform. However, those solutions are not purely regarded as exact solutions.

Due to the great diversity in the physical structure of non-Newtonian fluids, researchers have proposed a variety of mathematical models to understand the dynamics of such fluids. Mostly, these models fall in the subcategory of differential type fluids or rate types fluids. However, a keen interest of the researchers is seen in studying rate types fluids due to the fact that they incorporate both the elastic and memory effects together. The first and the simplest viscoelastic rate type model which is still used widely to account for fluid rheological effects is called Maxwell model1. This model can be generalized to produce a plethora of models. Initially, the Maxwell fluid model was developed to describe the elastic and viscous response of air. However, after that, it was frequently used to model the response of various viscoelastic fluids ranging from polymers to the earth’s mantle2,3,4. After the pioneering work of Friedrich5, on fractional derivatives of Maxwell fluid, several other investigations were carried out in this direction.

Among them,Haitao and Mingyu6 studied fractional Maxwell model in channel, Jamil et al.7 analyzed unsteady flow of generalized Maxwell fluid between two cylinders. In another investigation, Jamil et al.8, examined helices of fractionalized Maxwell fluid whereas Jamil9 analyzed slip effects on oscillating fractionalized Maxwell fluid. Corina et al.10 provided a short note on the second problem of Stokes for Maxwell fluids. Zheng et al.11, developed exact solutions for generalized Maxwell fluid for oscillatory and constantly accelerating plate motions, Zheng et al.12 used the same fluid model for heat transfer study due to a hyperbolic sine accelerating plate. Qi and Liu13 studied some duct flows of a fractional Maxwell fluid. Tripathi14 applied fractional Maxwell model to study peristaltic transport in uniform tubes.

Fetecau and Fetecau15, established a new exact solution for the flow of a Maxwell fluid past an infinite plate. In an other investigation, Fetecau and Fetecau16 determined exact solutions by means of the Fourier sine transforms for an incompressible fluid of Maxwellian type subjected to a linear flow on an infinite flat plate and within an infinite edge. Jordan et al.17 studied Stokes’s first problem for Maxwell fluids and obtained new exact solutions. Zierep and Fetecau18 examined energetic balance for the Rayleigh-Stokes problem of Maxwell fluid. Among some other important studies on Maxwell fluids, we mention here the important contributions of Jamil et al.19, Vieru and Rauf20, Vieru and Zafar21 and Khan et al.22. However, in all these investigations, heat transfer analysis was not considered. More exactly, phenomenon of heat transfer due to mixed convection was not incorporated in all the above studies. Therefore, the focal point of this work is to analyze Maxwell fluid over an oscillating vertical plate with constant wall temperature and to establish exact solutions using the Laplace transform method. The obtained results consideration of heat transfer analysis in Maxwell fluid has industrial importance since many problems of physical interest involve heat transfer such as automotive industry (radiator, cooling circuits, lamps), aerospace (de-icing system, cooling systems), in chemical process industry (heat recovery systems, heat exchangers), energy (kilns, boiler, cross flow heat exchangers, solar panels) and home appliance (ovens, household heaters)23,24,25.

Mathematical formulation of the problem

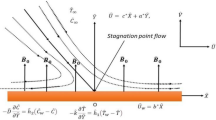
Let us consider unsteady mixed convection flow of an incompressible Maxwell fluid over an oscillating vertical flat plate moving with oscillating velocity in its own plane. Initially, at time t = 0, both the fluid and the plate are at rest with constant temperature T∞. At time t = 0+ the plate is subjected to sinusoidal oscillations so that the velocity on the wall is given by V = U0H(t)cos(ωt), resulting in the induced Maxwell fluid flow. More exactly, the plate begins to oscillate in its plane (y = 0) according to V = U0H(t)cos(ωt)i; where the constant U0 is the amplitude of the motion, H(t) is the unit step function, i is the unit vector in the vertical flow direction and ω is the frequency of oscillation of the plate. At the same time t = 0+, the temperature of the plate is raised or lowered to a constant value Tw. The velocity decays to zero and temperature approaches to a constant value T∞, also known as free stream temperature. The equations governing the Maxwell fluid flow related with shear stress and heat transfer due to mixed convection are given by the following partial differential equations:

The appropriate initial and boundary conditions are:

Introducing the following non-dimensional quantities:

into Eqs (1, 2, 3), we get

with the corresponding initial and boundary conditions:

Solution of the problem

Temperature

Taking Laplace transform of Eqs (8), (10)2, (11)2 and using initial condition (9)2, we obtain

The solution of the partial differential equation (12) subject to conditions (13) is given as:

Taking the inverse Laplace transform and using (A1), we obtain:

Velocity field

Taking the Laplace transform of Eqs (6), (10)1, (11)1 and using initial conditions, we obtain

Using Eq. (14) in Eq. (16), we have

Solve the partial differential Eq. (18), we have:

The last equality can be written in equivalent form as:

where .

Let

Taking the inverse Laplace transform of Eq. (21), we obtain:

Taking the inverse Laplace of Eq. (25), we obtain

where being Dirac distribution.

Applying inverse Laplace transform to Eq. (20) and using convolution product, we obtain

Shear stress

Applying Laplace transform to Eq. (7), we obtain

Differentiate Eq. (19) with respect to spatial variable , we obtain

Put Eq. (30) into Eq. (29), we obtain

where

Applying the inverse Laplace transform to Eqs (31), (32), (33) and (34), we obtain

with

where represents convolution product and is defined in Appendix (A3).

Solutions in the absence of Buoyancy force (limiting case)

In this case, when Gr = 0 the solution corresponding to oscillating boundary motion can easily be obtained from Eqs. (28) and (35). Such solutions are already obtained by Corina et al.10.

Newtonian fluid (λ = 0).

Velocity

Shear stress

where

Numerical results and discussions

The geometry of the problem is given in Fig. 1. In order to get some physical insight of the results corresponding to oscillating velocity on the boundary, some numerical calculations have been carried out for different values of pertinent parameters that describe the flow characteristics. All physical quantities and profiles are dimensionless. Also all profiles are plotted versus y. Figure 2 presents the temperature profiles for different values of time t and Prandtl number Pr variation. The fluid temperature is a decreasing function with respect to Prandtl number Pr and tends to a steady state slowly as the time t increases. Figure 3 presents the velocity profiles for different values of time t and Grashof number Gr variation. For other constant we have λ = 0.7, ω = 2, Pr = 5. It is observed that the fluid velocity is increased by increasing the Grashof number Gr. By increasing the time t the difference between the velocities as well as the steady state increases. Figure 4 presents the velocity profiles for different values of time t and Prandtl number Pr variation. For other constants, we have λ = 0.7, ω = 2, Gr = 5. It is observed that the fluid velocity decreases by increasing the Prandtl number Pr. By increasing the time t, the difference between the velocities as well as the steady state increases. Figure 5 presents the shear stress profiles for different values of time t and Grashof number Gr variation. For other constants, we have . It is observed that near the boundary the shear stress increases by increasing the Grashof number Gr but after some critical value of y the shear stress is decreased by increasing Gr. By increasing the time t the critical value of y is increased it means that the critical point is far from the boundary. Figure 4 presents the shear stress profiles for different values of time and Prandtl number Pr variation. For other constants we have λ = 0.3, ω = 2, Gr = 10. It is observed that the region near the boundary, the shear stress is decreased by increasing the Prandtl number Pr. By increasing the time t, Fig. 6 has the same behavior like Fig. 4. A comparison between Maxwell fluid and Newtonian fluid is shown graphically in Fig. 7.

Figure 1
figure 1

Velocity and temperature profiles for mixed convection flow over a hot vertical plate at Tw exposed to plate at T∞.

Full size image
Figure 2
figure 2

Profiles of temperature for Prandtl number Pr variation for different time t.

Full size image
Figure 3
figure 3

Profiles of velocity for Grashof number Gr variation for different time t.

Full size image
Figure 4
figure 4

Profiles of velocity for Prandtl number Pr variation for different time t.

Full size image
Figure 5
figure 5

Profiles of shear stress for Grashof number Gr variation for different time t.

Full size image
Figure 6
figure 6

Profiles of shear stress for Prandtl number Pr variation for different time t.

Full size image
Figure 7
figure 7

Profiles of velocities and shear stress for Maxwell fluid and Newtonian fluid.

Full size image

Conclusions

This study reports the first exact solution for unsteady mixed convection problem of Maxwell fluid via Laplace transform method. Expressions of velocity, shear stress and temperature are obtained and then plotted graphically for various embedded parameters. The solution corresponding to Newtonian fluid problem is recovered as a special case. Moreover, it is found that in the absence of free convection term, the already published results can be recovered as a special case. From the plotted results, it is found that temperature decreases with increasing Prandtl number; however, for large timethe temperature decays later. Velocity decreases with increasing Prandtl number whereas an oscillating behavior is observed for Grashof number.

Additional Information

How to cite this article: Khan, I. and Shah, N. A. A scientific report on heat transfer analysis in mixed convection flow of Maxwell fluid over an oscillating vertical plate. Sci. Rep. 6, 40147; doi: 10.1038/srep40147 (2016).

Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.