Introduction

Quantum entanglement has been a topic of great interest ever since the pioneering work was presented by Einstein et al.1 in 1935. It is defined as the nonseparability of quantum states2,3,4,5,6, and is one of the most important resources in quantum information processing. Notably, correlations arising from local measurements performed on separated entangled systems can exhibit nonlocal correlations7,8. In particular, the observed statistics cannot be reproduced using a local hidden variable model, as witnessed by violation of a Bell inequality2,3.

Originally, the phenomenon of Einstein-Podolsky-Rosen (EPR) steering (or quantum steering) was introduced by Schrödinger in 1935 to analyze the EPR-paradox9,10. Later, some theoretical and experimental works concerning quantum steering have been achieved11,12,13,14,15,16,17,18,19,20,21, and Wiseman et al.22,23 formulated steering in an operational way in conformity for a quantum information task. Recently, quantum steering was given an operational explanation as the distribution of entanglement by an untrusted party22, which depends on the question of whether Alice can convince Bob when they share an entangled state, although the fact that Bob distrust Alice. Then, Alice performs her measurements (which are unknown to Bob) and informs him of the results. If the correlations between Bob’s measurement results and those Alice reports cannot be explained by a local hidden states model (LHSM)23 for Bob, then Bob will believe that they share an entangled state. Quantum steering is an intermediate form of quantum correlation between Bell nonlocality2,8 and entanglement3 in modern quantum information theory. Furthermore, quantum steering can be detected via violating quantum steering inequality24. Derived for both continuous and discrete variable systems25,26,27,28,29, such steering inequalities can be obtained employing entropic uncertainty27,30. The significant steering criteria have been developed31,32,33,34,35,36,37 to detect steering from different aspects. These criterions can also be used to guarantee one-way steering15, namely, Alice can steer Bob, however Bob cannot steer Alice. And the one-way steering has been verified in some theoretical and experimental works11,12,13,14,15,16,17.

Despite previous fruitful achievements, however, these investigations mentioned are limited to the exploration of quantum steering in an isolated system. In a realistic regime, quantum systems unavoidably suffer from decoherence or dissipation arising from the interaction between the systems and its external noises38,39. Consequently, it is important to investigate quantum steering, nonlocality and entanglement under the influence of reservoirs (noisy channels), and establish whether the steerable state depends on reservoirs. As a matter of fact, there are a few authors to pay attention to address this problem40,41,42. In this work, some problems of that Alice can distantly steer Bob are investigated, and then we consider two different types of bipartite states (entangled pure state and entangled mixed state) as the initial states. Herein, we explore the performance of quantum steering, nonlocality and entanglement in the different reservoirs. Our analytical results indicate that: (i) All entangled pure states and maximally entangled evolution states are steerable. (ii) Not every entangled evolution state is steerable and some steerable states cannot violate Bell-CHSH inequality. (iii) Decoherence can rapidly induce the degradation of quantum steering, and the steerability of entangled pure states is stronger than that of entangled mixed states.

Results

Exploring the performance of quantum steering, entanglement and nonlocality of two-qubit X-state in the different reservoirs

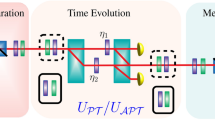
We assumed that there are two parties, Alice on Earth and Bob on the satellite, sharing a pair of entangled photons. Then we will elaborate the steering, nonlocality and entanglement in a physical case illustrated in Fig. 1(a) as following: Alice prepares a pair of entangled photons and sends one to Bob. The photon B in the process of transmission inevitably suffers from the different noisy environments43 (amplitude damping (AD), phase damping (PD), phase flip (PF) and bit flip (BF) channels). We will investigate the performance of quantum steering, nonlocality and entanglement for the evolution state described by a trace-preserving quantum operation ε(ρ), which is given by , where {Ei} is the set of Kraus operators associated to a decohering process of a single qubit, with the trace-preserving condition reading44 . Then, we provide lists of Kraus operators for varieties of quantum channels considered in Table 1. Here, we define that the entangled evolution states (EESs) are damped states, which the subsystem B of the initial bipartite state suffers from the quantum noisy channels. We will consider two different types of initial states, entangled pure state and entangled mixed state:

Figure 1
figure 1

(a)Schematic diagram of systems: there are two parties shared an entangled state. Alice on the Earth and Bob on the satellite. If Alice can prepare a pair of entangled photons, Then, Alice sends one subsystem (photon B) of entangled photon to Bob. The photon B in the process of transmission inevitably suffers from the different noises. The red E denote noisy environment. (b) Varieties of quantum-measure (EUR steering inequality, Bell-CHSH inequality and entanglement) as function of the state parameters α when they initially share an entangled pure state.

Full size image
Table 1 Kraus operators for the quantum channels:phase flip (PF), bit flip (BF), amplitude damping (AD) and phase damping (PD), where d and p are decoherence probabilities.
Full size table

Alice and Bob share an entangled pure state

Assume that they have |φ〉AB = cos α|00〉 + sin α|11〉, 0 < α < π/2 and can also be expressed as

Based on Eqs (10) and (19) in the section of Methods, we can obtain its entanglement C = sin(2α) and Bell-CHSH inequality , respectively. It is straightforward to insert Eq. (1) (via Eq. (17)) into Eq. (21) in the Methods, resulting in the analytical expression of entropic uncertainty relations (EUR) steering inequality for the density matrix ρ.

In order to better understand EUR steering inequality27,30 for a pair of arbitrary observables, we take advantage of the results of Walborn et al.26. The system is explained by a LHSM if and only if (iff) the joint measurement probability density can be expressed as29,30,31

where ρq(xB|λ) is the probability density (TPD) of measuring to be xB given the details of preparation in the hidden variable λ. The subscript q denotes that this is TPD arising from a single state. By applying the positivity of the continuous relative entropy45 between any couple of probability distributions, Walborn et al.26 argued that it is always the case for continuous observables (COs) in states allowing LHSM that , where hq(xB|λ) is the continuous Shannon entropy caused by TPD. Then, it is straightforward to show (as Walborn et al. did) that any state allowing a LHSM in position and momentum must satisfy

Note that here and throughout the paper the base of all logarithms is assumed to be 2. Subsequently, one notes that the same arguments used to develop LHSM constraints for COs can be employed to formulate LHSM constraints for discrete observables (DOs) as well27. Because the positivity of the relative entropy is a fact45 for both continuous and discrete variables, one can derive the corresponding local hidden states constraint for DOs in the same way: , where Hq(RB|λ) is the discrete Shannon entropy of Pq(RB|λ). Then, we immediately obtain a new entropic steering inequality for pairs of DOs27

where ΩB is the value , {|Ri〉} and {|Si〉} are the eigenbases of observables and in the same N-dimensional Hilbert space, respectively. We must realize that for any EUR, even some relating more than two observables, there is a corresponding steering inequality27. Sánchez-Ruiz46 developed EUR for complete sets of mutually unbiased observables , where i = {1, …, N}. The N is dimensionality of the system, it has been shown47 that there are complete sets of N + 1 mutually unbiased observables. We can obtain the EUR in even dimensional quantum systems. The EUR can be adapted into quantum steering inequality readily by substituting conditional entropies for marginal ones. In the same way as done to derive Eq. (4), we can obtain the EUR steering inequality27

where H(B|A) = H(ρAB) − H(ρA) is the conditional von Neumann entropy. In two dimensional quantum systems, in terms of Eq. (5), employing the Pauli X, Y, and Z measurements bases on each side, and then the EUR steering inequality can be read as27

As shown in Fig. 1(b), one can find that all entangled pure states are steerable and satisfy Bell nonlocality. Besides, the maximally entangled pure state (α = π/4) is maximally steerable, say, Alice can perfectly remotely steer Bob. Next, let us investigate the performance of entanglement, nonlocality and quantum steering in the different quantum noisy channels. For simplicity, we will not write out detailed calculation process. The corresponding each parameter expression of two-qubit EESs in Bloch decomposition and the parameters μ1, μ2, μ3 are given in Table 2.

Table 2 The corresponding expression of each parameter of two-qubit EESs in Bloch decomposition and the parameters μ1, μ2, μ3 are given in the different channels when Alice and Bob initially share an entangled pure state.
Full size table

To better understand the relationship between quantum steering and nonlocality in different noisy channels, we plot some graphs in Fig. 2. In AD channel, we can find that quantum steering decreases with the increase of decoherence strength, and until the state is unsteerable (i.e., the Bob does not trust Alice that they shared states are entangled) iff decoherence strength is very large (i.e., d > 0.95). And the Bell nonlocality disappear iff d > 0.5, that is, this correlation is only locality. Intuitively, the quantum steering and Bell nonlocality are very stronger iff their state is in a maximally entangled evolution one, meanwhile, decoherence strength should be small enough. Besides, in BF channel, we can obtain that quantum steering and Bell nonlocality are symmetrical about p = 0.5, and all steerable states can violate the Bell-CHSH inequality (see Fig. 2(c) and (d)).

Figure 2
figure 2

AD channel, contour plot of EUR steering inequality and Bell-CHSH inequality versus decoherence strength d and states parameters α in (a) and (b), respectively. The left side of red dotted line denotes the steering (shown in (a)) and Bell nonlocality (shown in (b)). For BF channel, contour plot of EUR steering inequality and Bell-CHSH inequality versus decoherence strength p and states parameters α in (c) and (d), respectively. The left and right sides of the X-form denote the steerable (shown in (c)) and Bell nonlocality (shown in (d)).

Full size image

Subsequently, the relationships among three quantum measures: entanglement, quantum steering and nonlocality in the different quantum channels are shown in Fig. 3. From the figure, one can obtain that every maximally entangled evolution state is maximally steerable state. Some EESs are unsteerable and some steerable states will not obey Bell nonlocality. However, in PD and PF channels, all EESs are steerable and satisfy Bell nonlocality. In addition, all steerable states can violate the Bell-CHSH inequality, but some EESs cannot give rise to steering in BF channel. Apart from that the steerability of the initial entangled state is destroyed by decoherence, quantum steering experiences a recovery with the increase of decoherence strength in BF and PF channels. Moreover, all EESs can violate EUR steering inequality and satisfy Bell nonlocality in PD and PF channels (shown as Fig. 3(ii), (iii) and (vi)). In AD channel, we can find that the symmetry of quantum steering (or nonlocality) of the initial state is destroyed, but that does not for quantum entanglement (see Fig. 3(vi)).

Figure 3
figure 3

A variety of quantum-measure (EUR steering inequality, Bell-CHSH inequality and entanglement) as function of decoherence strength d, p for the maximally entangled state α = π/4(shown in (i), (ii) and (iii)). Quantum-measure as function of decoherence strength p for α = π/8 (shown in (iv) and (v)). (vi) The quantum-measure as function of state parameters α for d = 0.3.

Full size image

Alice and Bob share an entangled mixed state

Considering the mixed state35

where and . It is entangled when . Then, we still consider previous physical case as shown in Fig. 1(a). For convenience, we display the corresponding each parameter expression of two-qubit EESs in Bloch decomposition in Table 3.

Table 3 The corresponding expressions of each parameter of two-qubit EESs in Bloch decomposition are given in the different noisy channels when Alice and Bob initially share an entangled mixed state.
Full size table

In order to better comprehend the relationship among entanglement, quantum steering and nonlocality in the different types of noises, we draw the counterpart contour plots in Fig. 4. From the figure, we can obtain that all EESs’ entanglement; steering and nonlocality will experience a “sudden death”. Some EESs are unsteerable and some steerable states do not obey Bell nonlocality in AD channel. In addition, some results are not the same as the above case (the initial state is an entangled pure state). We find that all EESs can be employed to realize steering and satisfy Bell nonlocality in BF channel. However, in PD channel, all steerable states can violate the Bell-CHSH inequality, but some EESs cannot violate EUR steering inequality. Furthermore, in AD channel, decoherence can destroy the steerability of the initial state, and until the EESs cannot steer (d > 0.7), and the Bell nonlocality is absent iff d > 0.5. Moreover, quantum steering experiences a recovery with increasing state parameters v when decoherence strength is a fixed value in any noisy channel.

Figure 4
figure 4

Contour plot of entanglement (concurrence), EUR steering inequality and Bell-CHSH inequality versus decoherence strength d and states parameters v, AD channel shown in (a1), (b1) and (c1); PD channel shown in (a2), (b2) and (c2), respectively. The bottom of the red dotted line denotes the steering (see (b1) and (b2)) and Bell nonlocality (see (c1) and (c2)). For BF channel, contour plot of entanglement (concurrence), EUR steering inequality versus decoherence strength p and states parameters v in (a3), (b3) and (c3), respectively, when initial state is an entangled mixed state.

Full size image

Via the analysis, one can conclude that the steerability of entangled mixed states is weaker than the steerability of entangled pure states, and the steerability of state is associated with the interaction between quantum systems and quantum channels. Furthermore, the steering behaves sometimes like the nonlocality and sometimes like the entanglement. That is, quantum steering is an intermediate form of quantum correlation between entanglement and nonlocality.

Conclusions

To conclude, we analytically derive the performance of quantum steering, nonlocality and entanglement, and discuss the relationship among them in structured reservoirs for two different types of initial states: entangled pure state and entangled mixed state. Our results indicate that the steerability of entangled pure states is stronger than that of entangled mixed states, and entangled pure states and the maximally EESs are steerable. Not every entangled evolution state is steerable and some steerable states cannot violate Bell-CHSH inequality. In other words, if an entangled state shared by Alice and Bob is steerable, when the state suffers from the reservoirs, the state may be unsteerable, meanwhile, the Bell nonlocality may be absent.

Importantly, we find that all EESs can violate EUR steering inequality and Bell-CHSH inequality in PD and PF channels when they initially share an entangled pure state. In BF channel, all steerable states can satisfy Bell nonlocality, but some EESs are unsteerable. However, when they initially share an entangled mixed state, all EESs can be employed to realize steering and can lead to Bell nonlocality in BF channel. Moreover, decoherence can effectively induce the degradation of quantum steering, nonlocality and entanglement. However, these quantum correlations experience a recovery with the increase of decoherence strength in BF and PF channels. Therefore, we could say, the steerability of state is associated with the interaction between quantum systems and external noises.

Methods

Quantum entanglement, nonlocality and steering of two-qubit X-state

We first introduce the form of two-qubit X-state. The X-shaped states, which are represented in the orthonormal basis as

where ρij(i, j = 1, 2, 3, 4) are all real parameters. As is well known, the degree of entanglement for bipartite states can be quantified conveniently by concurrence. Hence, we chose concurrence as entanglement measurement. The concurrence is defined as48,49

where λi(i = 1, 2, 3, 4) are the eigenvalues of the matrix . The density matrix is X-structure, there is a reduced form for concurrence shown as ref. 50

where ρij are the elements of the matrix ρX. Thus, employing Eq. (10), we can obtain the expressions of concurrence in the different quantum channels , , respectively, when the initial state is an entangled pure state (1).

While initial state is an entangled mixed state (7), the concurrence in the different quantum channels can be expression as

with

respectively. Then, by employing appropriate local unitary transformations, one can rewrite the state of Eq. (8) in Bloch decomposition

where and are Bloch vectors, and are standard Pauli matrices. If , ρX is the a two-qubit Bell-diagonal state. Assume that Bloch vectors are in the z direction, that is, , the density matrix of ρX in Eq. (15) has the following form

with

According to the Horodecki criterion2,3, with i, j = 1, 2, 3. The three eigenvalues μi of U = TTT for X-state are

It is easy to see that μ1 is always larger than μ2, and thus the Bell Clauser-Horne-Shimony-Holt (Bell-CHSH) inequality maximum violation of X-state is refs 51, 52, 53

When Alice and Bob initially share an entangled mixed state (7), we can obtain the expressions of Bell-CHSH inequality in the different quantum channels

, , , (20)respectively. Subsequently, depending upon EUR steering inequality’s definition in Eq. (6), employing the X-state ρX in Eq. (16), we can obtain the expression of EUR steering inequality for the general bipartite X-state by using Pauli X, Y, and Z measurements on each side

If r = s = 0, the bipartite X-state will become the Bell-diagonal states. The Eq. (21) is simplified into30 . As an explanation, employing measurement in the Pauli X bases on each side, the four eigenvalues of the bipartite X-state are , and the two eigenvalues of the reduced state are . In the same way, we can obtain that the eigenvalues of the other two bipartite X-state are {λy1 = λy2 = (1 − c2)/4, λy3 = λy4 = (1 + c2)/4} and {λz1 = (1 − c3 + r − s)/4, λz2 = (1 − c3 − r + s)/4, λz3 = (1 + c3 + r + s)/4, λz4 = (1 + c3 − r − s)/4} by using Pauli Y and Z measurements on each side, respectively. The corresponding the eigenvalues of the reduced states , are and , respectively. Then, it is straightforward to insert all above eigenvalues into Eq. (6), we can obtain the expression of EUR steering inequality. Finally, it is straightforward to insert each parameter of Tables 2 and 3 into Eqs (19) and (21), resulting in the analytical expressions of Bell-CHSH inequality and EUR steering inequality.

Additional Information

How to cite this article: Sun, W.-Y. et al. Exploration quantum steering, nonlocality and entanglement of two-qubit X-state in structured reservoirs. Sci. Rep. 7, 39651; doi: 10.1038/srep39651 (2017).

Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.