Introduction

In 1935, the famous Einstein, Podolsky and Rosen (EPR) paper indicated that quantum mechanics is in conflict with the notion of locality and reality1. If local realism is correct, then quantum mechanics cannot be considered as a complete theory to describe physical reality. Immediately after the publication of the EPR paper, Schrödinger made a response by conjuring two important notions, namely, the quantum entanglement and the quantum steering. According to Schrödinger, quantum entanglement is “the characteristic trait of quantum mechanics” that distinguishes quantum theory from classical theory2. The notion of “steering” is closely related to the statement of “spooky action at a distance”, which Einstein was disturbed all the time. EPR steering reflects such a “spooky action” feature that manipulating one object seemingly affects another instantaneously, even it is far away.

Different to Schrödinger’s response, in 1964, Bell proposed an inequality for local hidden variable (LHV) models3. The violation of Bell’s inequality by quantum entangled states implies Bell’s nonlocality. This is well-known as Bell’s theorem, which has established what quantum theory can tell us about the fundamental features of Nature, and been widely regarded as “the most profound discovery of science”4. Until now, the fundamental theorem has achieved ubiquitous applications in different quantum information tasks, such as quantum key distribution5, communication complexity6, and random number generation7.

Unlike quantum entanglement and Bell’s nonlocality, the research field of quantum steering has been sterile till 2007, when Wiseman, Jones, and Doherty8 reformulated the idea and placed it firmly on a rigorous ground. Since then EPR steering has gained a very rapid development in both theories9,10,11,12,13,14,15,16 and experiments17,18,19,20,21,22,23,24,25,26. Most research topics as well as research approaches in the field of Bell’s nonlocality have been transplanted similarly to the field of EPR steering. For instance, steering inequalities have been proposed to reveal the EPR steerability of quantum states, very similar to the violation of Bell’s inequalities reveals Bell’s nonlocality.

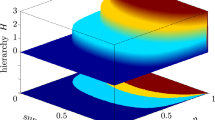
According to ref. 8, entanglement, EPR steering and Bell’s nonlocality are called by a joint name as “ quantum nonlocality”, which has an interesting hierarchical structure: quantum entanglement is a superset of steering, and Bell’s nonlocality is a subset of steering. However, among the three types of quantum nonlocality, only steering can possess a curious feature of “one-way quantumness”. Suppose Alice and Bob share a pair of two-qubit state, it is not hard to imagine that if Alice entangles with Bob, then Bob must also entangle with Alice. Such a symmetric feature holds for both entanglement and Bell nonlocality. However, the situation is dramatically changed when one turns to a novel kind of quantum nonlocality in the middle of entanglement and Bell nonlocality, the EPR steering. It may happen that for some asymmetric bipartite quantum states, Alice can steer Bob but Bob can never steer Alice. This distinguished feature would be useful for some one-way quantum information tasks, such as quantum cryptography. The “one-way EPR steering” or “asymmetric EPR steering” is an important “open question” first proposed by Wiseman et al. in ref. 8. Very recently, the question has been answered by Bowles et al.15, who presented a simple class of one-way steerable states in a two-qubit system with at least 13 projective measurements (a linear 14-setting steering inequality was given explicitly in the work). The inspiring result for the first time theoretically confirms quantum nonlocality can be fundamentally asymmetric. Later on, Bowles et al. investigated the one-way steering problem by presenting a sufficient criterion (being a nonlinear criterion) for guaranteeing that a two-qubit state is unsteerable27.

In this work, we focus on another curious quantum phenomenon raised by steering: Bell nonlocal states can be constructed from some EPR steerable states. Explicitly we present a theorem, showing that for any two-qubit state τ, if its corresponding state ρ is EPR steerable, then the state τ must be Bell nonlocal. Bell’s nonlocality of the quantum state τ can be detected indirectly by the violation of steering inequality for the quantum state ρ. The novel result not only pinpoints a deep connection between EPR steering and Bell’s nonlocality, but also sheds a new light to avoid locality loophole in Bell’s tests and make Bell’s nonlocality easier for demonstration. In addition, we also present a 9-setting linear steering inequality for developing more efficient one-way steering and detecting some Bell nonlocal states. We find that the new steering inequality can actually improve the result of ref. 15 by detecting the one-way steering with fewer measurement settings but with larger quantum violations, which would be helpful for the experimenters.

Results

Bell’s Nonlocal states can be constructed from EPR steerable states

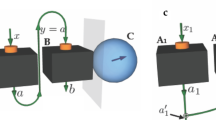
It is well-known that quantum nonlocality possesses an interesting hierarchical structure (see Fig. 1). EPR steering is a weaker nonlocality in comparison to Bell’s nonlocality. Here we would like to pinpoint a curious quantum phenomenon directly connecting these two different types of nonlocality. We find that Bell’s nonlocal states can be constructed from some EPR steerable states, which indicates that Bell’s nonlocality can be detected indirectly through EPR steering (see Fig. 2), and offers a distinctive way to study Bell’s nonlocality. The result can be expressed as the following theorem.

Figure 1
figure 1

Hierarchical structure of quantum nonlocality.

Bell’s nonlocality is the strongest type of quantum nonlocality. If a state possesses EPR steerability or Bell’s nonlocality, then the state must be entangled. EPR steering is a form of nonlocality intermediate between entanglement and Bell nonlocality.

Full size image
Figure 2
figure 2

Illustration of detecting Bell’s nonlocality through EPR steering.

If a state ρAB violates a steering inequality, then it implies that ρAB possesses the EPR steerability. Traditionally, Bell’s nonlocality of the two-qubit state τAB is revealed by violations of Bell’s inequality. Based on Theorem 1, Bell’s nonlocality of the state τAB can be detected through EPR steerability of the state ρAB, and the relation between ρAB and τAB is given in Eq. (1).

Full size image

Theorem 1: For any two-qubit state τAB shared by Alice and Bob, define another state

with , being the reduced density matrix at Alice’s side, and . If ρAB is EPR steerable, then τAB is Bell nonlocal.

Proof. The implication of the theorem is that, the EPR steerability of the state ρAB determines Bell’s nonlocality of the state τAB. Namely, the nonexistence of local hidden state (LHS) model for ρAB implies the nonexistence of LHV model for τAB. We shall prove the theorem by proving its converse negative proposition: if the state τAB has a LHV model description, then the state ρAB has a LHS model description.

Suppose τAB has a LHV model description, then by definition for any projective measurements A for Alice and B for Bob, one always has the following relation

Here is the joint probability, quantum mechanically it is computed as , is the projective measurement along the -direction with measurement outcome a for Alice, is the projective measurement along the -direction with measurement outcome b for Bob (with a, b = 0, 1), , and Pξ denote some (positive, normalized) probability distributions.

Let the measurement settings at Bob’s side be picked out as x, y, z. In this situation, Bob’s projectors are , , , respectively. Since the state τAB has a LHV model description, based on Eq. (2) we explicitly have (with )

We now turn to study the EPR steerability of ρAB. After Alice performs the projective measurement on her qubit, the state ρAB collapses to Bob’s conditional states (unnormalized) as

To prove that there exists a LHS model for ρAB is equivalent to proving that, for any measurement and outcome a, one can always find a hidden state ensemble and the conditional probabilities , such that the relation

is always satisfied. Here ξ’s are the local hidden variables, ρξ’s are the hidden states, and are probabilities satisfying and . If there exist some specific measurement settings of Alice, such that Eq. (5) cannot be satisfied, then one must conclude that the state ρAB is steerable (in the sense of Alice steers Bob’s particle).

Suppose there is a LHS model description for ρAB, then it implies that, for Eq. (5) one can always find the solutions of if Eq. (3) is valid. The solutions are given as follows:

where is the 2 × 2 identity matrix, is the vector of the Pauli matrices, and the hidden state ρξ has been parameterized in the Bloch-vector form, with

which is the Bloch vector for density matrix of a qubit. It can be checked that , and this ensures ρξ being a density matrix.

By substituting Eq. (6) into Eq. (5), we obtain

To prove the theorem is to verify the relation (8) is always satisfied if Eq. (3) is valid. The verification can be found in Methods.

Remark 1.— In Eq. (7), by requiring the condition be valid for any probabilities P(0|x, ξ), P(0|y, ξ), P(0|z, ξ) ∈ [0, 1], in general one can have . Generally, Theorem 1 is valid for any . In the theorem we have chosen the parameter μ as its maximal value , because the state τAB is convexed with a separable state , the larger value of μ, the easier to detect the EPR steerability.

In the following, we provide two examples for the theorem, showing that Bell’s nonlocality of quantum states can be detected indirectly by the violations of some steering inequalities.

Example 1.— For example, let us detect Bell’s nonlocality of the maximally entangled state (with τAB = |Ψ〉 〈Ψ|)

without Bell’s inequality. Based on the theorem, it is equivalent to detect the EPR steerability of the following two-qubit state

with . The state (10) is nothing but the Werner state28 with the visibility equals to , its steerability can be tested by using the steering inequality proposed in ref. 17 as

with N = 6. Here is the steering parameter for N measurement settings, and CN is the classical bound, with . The maximal quantum violation of the steering inequality is , which beats the classical bound.

Remark 2.— In a two-qubit system, Bell’s nonlocality is usually detected by quantum violation of the Clause-Horne-Shimony-Holt inequality29. Bell’s nonlocality is the strongest type of nonlocality, due to this reason Bell-test experiments have encountered both the locality loophole and the detection loophole for a very long time30. As a weaker nonlocality, EPR steering naturally escapes from the locality loophole and is correspondingly easier to be demonstrated without the detection loophole19,20, as stated in ref. 17: “because the degree of correlation required for EPR steering is smaller than that for violation of a Bell inequality, it should be correspondingly easier to demonstrate steering of qubits without making the fair-sampling assumption [i.e., closing the detection loophole]”. Indeed, the steerability of the Werner state has been experimentally detected in ref. 17 by the steering inequality (11). Our result shows that the EPR steerability of the state ρAB determines Bell’s nonlocality of the state τAB, thus may shed a new light to realize a loophole-free Bell-test experiment through the violation of steering inequality.

Example 2.— The theorem naturally provides a steering-based criterion for Bell’s nonlocality, which is expressed as follows: given an EPR steerable two-qubit state ρAB, if the matrix

is a two-qubit density matrix, then τAB is Bell nonlocal.

Let us consider a two-qubit state ρAB in the following form

By substituting the state ρAB as in Eq. (13) into Eq. (12), then one obtains

with

It is worth to mention that the steering inequality (11) is applicable to show Bell’s nonlocality of τAB for some parameters α′, β′, γ′. Here we would like to show that the similar task can be done by other new steering inequalities. In the following, we present a 9-setting linear steering inequality as

here for convenient we have used the same notations as in ref. 15 (where (σ1, σ2, σ3) is equivalent to (σx, σy, σz)). The inequality are characterized by matrices {S, SA, SB} with real coefficients sij, , and , and the local bound is L = 1 (see Supplementary Materials). The steering inequality (16) may have other particular application for improving the result ref. 15 by developing more efficient one-way steering, which we shall address in the coming section. But now we use it to detect Bell’s nonlocality.

For example, let α′ = 0.96, β′ = −1/5, γ′ = 1/6, ones finds that τAB is a two-qubit state, and the steering inequality (16) is violated by the state ρAB (with the violation value 1.0064), hence the Bell’s nonlocality of state τAB can be revealed in this way indirectly by the steerability of the state ρAB.

More efficient one-way EPR steering

Under local unitary transformation (LUT), any two-qubit state can be written in the following form ref. 31

with β, γ, tk being the real coefficients, and , the unit vectors. Obviously, under LUT, the state ρAB is said to be symmetric if and only if β = γ and . Let one consider a simple situation with t1 = t2 = t3 = −α, and , then he obtains the two-qubit state ρAB as in Eq. (13). In such a case, if ρAB is a one-way steerable state, then one must have β ≠ γ.

In ref. 15, the authors have chosen , and used the SDP program to numerically prove that the state ρAB is a one-way steerable state (with at least 13 projective measurements): for α ≤ 1/2, the state ρAB is unsteerable from Bob to Alice, while for the state is steerable from Alice to Bob when Alice performs 14 projective measurements. An explicit 14-setting steering inequality has been also proposed to conform the one-way steerability, although for α = 1/2, the quantum violation is tiny (only 1.0004). The inspiring result for the first time confirms that the nonlocality can be fundamentally asymmetric. However, the tiny inequality violation as well as the 14 measurement settings give rise to the difficulty in experimental detection. To advance the study of unidirectional quantum steering, here we present a more efficient class of one-way steerable states by choosing

with α ∈ [0, 1]. The state ρAB(α) is entangled for α > 0.3279. With the help of the SDP program, we found that in the range , the state ρ(α) is one-way steerable within 10-setting measurements, thus this is more efficient than the previous result in ref. 15 (For the detail derivation of more efficient one-way EPR steering see Supplementary Materials). Furthermore, we can extract an explicit 9-setting steering inequalities (16) based on the SDP program. It can be verified directly that, for the state ρAB(1/2), the quantum violation of 9-setting inequality (16) is , hence demonstrating steering from Alice to Bob. Compared to the previous result15, the amount of violation is much larger but achieved with fewer measurements. To our knowledge, we do not know whether the quantum violation by inequality (16) could be observed with current quantum technology. However, we believe that this result would be interesting and helpful for both theoretical and experimental physicists.

Discussion

In this work, we have presented a theorem showing that Bell nonlocal states can be constructed from some EPR steerable states. This result not only offers a novel and distinctive way to study Bell’s nonlocality with the violation of steering inequality, but also may avoid locality loophole in Bell’s tests and make Bell’s nonlocality easier for demonstration. An interesting and inverse problem is whether one can construct some steerable states τAB from some Bell nonlocal state ρAB, because Bell’s nonlocality has been researched more deeply in theoretical aspect, so that people can conveniently study steering via known criteria of Bell’s nonlocality. Furthermore, an explicit 9-setting linear steering inequality has also been presented for detecting some Bell nonlocal states and developing more efficient one-way steering. This result allows one to observe one-way EPR steering with fewer measurement setting but with larger quantum violations. We hope experimental progress in this direction could be made in the near future.

Methods

Verification of equation (8)

Let us calculate the left-hand side of Eq. (8). One has

where is the marginal probability of Alice when she measures A and gets the outcome a. For convenient, let us denote the 2 × 2 matrix as

and calculate its each element. We get

and similarly,

Note that , we then have

Because

with Re[ν12] is the real part of ν12, thus,

Similarly, because

with Im[ν12] is the imaginary part of ν12, thus,

By combining the above equations, we finally have

Let us calculate the right-hand side of Eq. (8). It gives

With the help of Eq. (3) and using , we finally have

By comparing Eqs (19) and (20), it is easy to see that Eq. (8) holds. Thus, if there is a LHV model description for τAB, then there is a LHS model description for ρAB. This completes the proof.

Additional Information

How to cite this article: Chen, J.-L. et al. Bell’s Nonlocality Can be Detected by the Violation of Einstein-Podolsky-Rosen Steering Inequality. Sci. Rep. 6, 39063; doi: 10.1038/srep39063 (2016).

Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.