Abstract
For large quantities of spatial models, the multi-strategy selection under weak selection is the sum of two competition terms: the pairwise competition and the competition of multiple strategies with equal frequency. Two parameters σ1 and σ2 quantify the dependence of the multi-strategy selection on these two terms, respectively. Unlike previous studies, we here do not require large populations for calculating σ1 and σ2, and perform the first quantitative analysis of the effect of migration on them in group-structured populations of any finite sizes. The Moran and the Wright-Fisher process have the following common findings. Compared with well-mixed populations, migration causes σ1 to change with the mutation probability from a decreasing curve to an inverted U-shaped curve and maintains the increase of σ2. Migration (probability and range) leads to a significant change of σ1 but a negligible one of σ2. The way that migration changes σ1 is qualitatively similar to its influence on the single parameter characterizing the two-strategy selection. The Moran process is more effective in increasing σ1 for most migration probabilities and the Wright-Fisher process is always more effective in increasing σ2. Finally, our findings are used to study the evolution of cooperation under direct reciprocity.
Similar content being viewed by others
Introduction
Populations are usually divided into several subpopulations separated by geographical distance. Migration, linking subpopulations, is one of the oldest adaptation measures in the animal kingdom and human society. The effect of migration on developing such populations has attracted researchers from various fields. Masses of related analytic studies have been performed by geneticists and mathematicians to explain the correlation between genetic distance and geographic distance through the (one-dimensional or two-dimensional) stepping-stone models1,2,3,4,5. The update rules most extensively used are the frequency-independent Moran process and the frequency-independent Wright-Fisher process.
The above-mentioned studies assume that all individuals have the same fitness. Nonetheless, most realistic settings do not operate in this way, and individuals’ fitness is shaped by the behaviors of themselves together with those who live in the same environment. Evolutionary game theory provides a powerful mathematical framework to deal with such interactions6,7,8,9,10. Under the framework, spatial models have attracted more and more attention through games on graphs11,12,13,14,15,16,17 and populations comprised of subpopulations18,19,20,21,22,23,24,25,26,27. For a large class of spatial models, including games in phenotype space28, games on sets29, games on islands30, and games in group-structured populations31, the two-strategy selection and the multi-strategy selection under weak selection can be characterized by a single parameter32 and two parameters33, respectively. Weak selection, meaning the fitness varies little among individuals, has been widely used for analytical studies34,35,36,37,38,39,40,41,42. Prior research has showed that the results under weak selection, in general, could not be extrapolated to strong selection43,44. There are two reasons why weak selection is still so popular is as follows: Weak selection makes it possible to obtain analytical results without additional assumptions; Weak selection is a natural situation in which a particular game makes a small contribution on the overall fitness of individuals, for example, (a) strategies are similar (as in the adaptive dynamics45,46), (b) individuals get confused about payoffs during the strategy update.
When a game between two strategies (say 1, 2) described by the payoff matrix (aij)2 × 2 (aij is the payoff of an individual using i when interacting with an individual using j) is considered32, strategy 1 is more abundant than strategy 2 on average under weak selection if
The parameter σ quantifies the influence of the population structure (including the update rule) on the two-strategy selection. When a game among S ≥ 3 strategies (say 1, 2, …, S) described by the payoff matrix (aij)S×S (similar to (aij)2×2) is considered33, the average frequency of strategy k ∈ {1, 2, …, S} over the stationary distribution is greater than 1/S under weak selection if
where 
, 
, 
, and 
. It indicates that the multi-strategy selection is simply the sum of two competition terms. The first term, 
, demonstrates an average over all pairwise comparisons between strategy k and any other strategies, and the second, 
, the competition of all S strategies when they have the equal frequency 1/S. Accordingly, the parameters σ1 and σ2 quantify the effect of the population structure on the pairwise competition and the competition of all strategies with equal frequency, respectively. Moreover, they quantify the dependence of the multi-strategy selection on these two competition terms, respectively.
It has been showed that the above-mentioned parameters σ, σ1, and σ2 do not depend on the entries of the payoff matrix but rely on the population structure (including the update rule)32,33. Two previous studies have investigated the effect of migration on σ in large finite populations30 and any finite populations47, respectively. The values of σ1 and σ2 have been obtained for large finite populations33, but it is still unknown how varying migration patterns affect them in populations of any finite sizes.
In this paper, we will calculate the concrete values of σ1 and σ2 for group-structured populations of any finite sizes. Our study will proceed for the frequency-dependent Moran process (hereafter called the Moran process without ambiguity) and the frequency-dependent Wright-Fisher process (hereafter called the Wright-Fisher process). The Moran process represents an idealized case of overlapping generations and the Wright-Fisher process is a perfect case of non-overlapping generations. The realistic society cannot be fully depicted by either of them, and yet maybe by something in between. Under the assumption of large populations, it is known that the calculation procedures of σ1 and σ2 are the same for the Moran and the Wright-Fisher process when the same symbol represents the product of the population size and the mutation probability in the former and twice the product in the latter28. However, the two calculation procedures vary significantly in populations of any finite sizes and will be separately given in Supplementary Information. The key point for obtaining σ1 and σ2 is to calculate some special probabilities under neutral selection33. The corresponding probabilities for the Moran process have been derived in group-structured populations of any finite sizes31, and they will be applied to our model to get σ1 and σ2. Meanwhile for the Wright-Fisher process, we will acquire the corresponding probabilities for group-structured populations of any finite sizes, and then use them to calculate σ1 and σ2. For either of the two processes, the expressions of σ1 and σ2 given later hold for any ‘isotropic’ migration patterns, and a particular migration pattern fully captured by the migration range will be employed to clarify how the migration range impacts σ1 and σ2. We will compare the qualitative and the quantitative effect of the two processes on σ1 and σ2. Finally, our findings will be used to study the evolution of cooperation under direct reciprocity by considering the competition of ALLC, ALLD, TFT.
Results
Model description
Consider a group-structured population of size N which is fragmented into M groups (subpopulations). A group can be understood as an island in population genetics, and a particular company or a living community in human society. An individual adopts one of S strategies labelled as 1, 2, …, S and the payoff matrix is given by (aij)S×S, where aij is the payoff of an individual using i against an individual using j. An individual only plays the game with all others of the same group. Interactions produce the payoff of an individual (say k), pk, and further his fitness, fk = 1 + δpk, where δ ≥ 0 is the selection intensity. In this paper, the case of weak selection, δ → 0, is our focus.
The Moran process and the Wright-Fisher process will be analyzed, respectively. In the Moran process, all individuals of the population compete to reproduce one offspring proportional to their fitness, and then one individual is equi-probably chosen from the whole population to die. In the Wright-Fisher process, all individuals compete to reproduce N (population size) offspring proportional to their fitness, and the whole population is replaced by all the newborn offspring. Mutation or migration may happen to the offspring. An offspring mutates with probability u and then he follows the pattern of ‘global mutation’ to choose one strategy, i.e., one of S strategies is chosen equi-probably; Otherwise (with probability 1 − u), the offspring inherits the strategy of his parent. An offspring migrates with probability v and then he moves to one group according to a pre-defined migration pattern; Otherwise (with probability 1 − v), the offspring remains in his parent’s group.
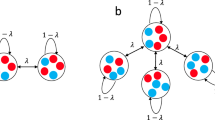
An undirected graph is used to illustrate the pattern of migration among the M groups arranged in a circle. Each node represents a group and an edge is a potential single-step migration path. We focus on the case of vertex-transitive graphs (with or without self-circle), which are homogeneous in the sense that they look the same from every node. Such migration patterns are ‘isotropic’ and have been widely investigated1,2,3,4,5,30,31. Examples include ‘local migration’ in which a single-step migration occurs equi-probably among all pairs from neighboring nodes or ‘global migration’ in which a single-step migration is equally likely to take individuals to any other nodes30. In this paper, the concrete values of σ1 and σ2 will be obtained for any ‘isotropic’ migration patterns, and then a particular migration pattern fully captured by the migration range r (Fig. 1) will be analyzed. The migration range r, which takes on one of the values 
(
is the greatest integer not greater than x), means that all possible displacements generated by a single-step migration form the set Ω(r) = {1, 2, …, r} whose elements are performed equi-probably. The above-mentioned ‘local migration’ and ‘global migration’ can be characterized by r = 1 and 
, respectively.
Migration patterns characterized by the migration range r.
Seven groups (orange nodes) are arranged in a regular circle and labelled from 1 to 7 in clockwise. An edge exists between two nodes if and only if there is a potential single-step migration path between them. In other words, an offspring can migrate to one of the nodes connected to the node in which his parent is located. The distance between two groups takes on one of the values 1, 2, 3. The migration range r means that the displacements generated by a single-step migration form the set Ω(r) = {1, …, r} whose elements are performed equiprobably.
In the above model, migration occurs after reproduction. We also consider a second case in which migration occurs before reproduction and the rest follows from the procedure above. Specifically, one individual is chosen equi-probably (from the whole population) to migrate before reproduction in the Moran process, and all individuals migrate before reproduction in the Wright-Fisher process. The corresponding results are qualitatively similar to but quantitatively different from those of the initial case by Monte-Carlo simulations (Supplementary Information), and will not be given in the main text. The quantitative difference emerges because mutation and migration in the second case cannot happen to the same individual during a generation, which happens in the initial case.
The Moran process
The parameters σ1 and σ2 can be expressed by the probabilities (under neutral selection) assigned to the event that three randomly chosen (without replacement) individuals use given strategies and locations (see Methods for the detailed calculations). The expression of such probabilities has been derived for any mutation patterns and migration patterns31. Applying the expression to ‘global mutation’ of our model (see Supplementary Information: III and Methods for the detailed calculations), we have σ1 and σ2 of the Moran process denoted by 
and 
in the following expressions in which Φi(f(x)) and Ψi(f(x)) are abbreviated as Φi and Ψi.
where 
, 
, 
, 
, 
, 
, 
, 
.
The expressions hold for any ‘isotropic’ migration patterns described by f(x). To better clarify how the migration range affects σ1 and σ2, we focus on a representative type of migration patterns characterized by the migration range r (Fig. 1) whose corresponding f(x) is
Besides the migration pattern, the expressions have no limitations on the non-zero mutation probability, the migration probability, the population size, or the group number. Figure 2 shows that the theoretical values of 
and 
agree well with the simulated values for different mutation probabilities (u), migration probabilities (v), population sizes (N), group numbers (M), and migration ranges (r). It is noteworthy that the number of strategies S does not appear in the expressions of 
and 
, which agrees with the known conclusion that they are independent of S33.
The theoretical values of 
and 
are in agreement with the simulated values.
The solid line describes the theoretical values of 
(a,b) or of 
(c,d). The square denotes the simulated values of 
(a,b) or of 
(c,d) averaged over 109−106 generations (starting to record at generation 106). Parameters: (a,c) v = 1, N = 100, M = 19, r = 1; (b,d) u = 0.1, N = 50, M = 9, r = 4.
After simple calculations, we have 
and 
in the limit u → 0 as
The pairwise competition plays an overriding role in determining the multi-strategy selection for extremely low mutation probabilities. It is intuitive since there exist simultaneously at most two strategies in the population. By letting u = 1 in equation (3), we get 
and 
for u = 1 as
The competition of multiple strategies with equal frequency plays an overriding role in affecting the multi-strategy selection for sufficiently large populations and mutation probabilities (the condition for strategy k to be favored becomes 
).
It is easy to calculate 
and 
for v = 0 as
As the mutation probability u increases, the pairwise competition fades out of the multi-strategy selection and the competition of multiple strategies with equal frequency gradually dominates the multi-strategy selection. In the absence of migration (v = 0), the long-term population, in which the absorbing state is that all individuals are located in one group, evolves just like the well-mixed population. Therefore, equation (7) also gives the values of 
and 
for the well-mixed population. For large populations, 
and 
are approximated as 1 and Nu respectively, which is in agreement with the previous study48.
When there exists migration (v ≠ 0), the comparison of 
and 
(the dependence of the multi-strategy selection on the pairwise competition and the competition of multiple strategies with equal frequency) is still mainly determined by the mutation probability u (Fig. 3a,b). In contrast to the well-mixed population (or v = 0), in which 
decreases monotonically with the increase of u, migration (moderate migration probabilities) causes the change of 
with respect to u to exhibit an inverted U-shaped curve. Similar to the well-mixed population (or v = 0), the value of 
is still proportional to u with a coefficient around the population size N. This verifies the previous conjecture33 that σ1 ≪ σ2 holds for large Nu. Low mutation probabilities which are extremely close to zero lead to 
, which means that the pairwise competition has an advantage over the competition of multiple strategies with equal frequency in determining the multi-strategy selection. Whereas the remaining vast majority of mutation probabilities result in 
, which means that the competition of multiple strategies with equal frequency gains the advantage over the pairwise competition.
The changing trends of 
and 
.
(a) As u increases, 
decreases for low v and high v (not shown), and exhibits an inverted U-shaped curve for moderate v. 
expands quickly as u increases. For very low u, 
is greater than 
(inset). For a little higher u, 
is smaller than 
, and the difference will expand quickly as u increases. (b) As u increases, 
expands nearly linearly with a high speed of around N. r leads to a negligible change of 
. (c) v or r results in a significant change of 
but a relatively negligible change of 
. A moderate v maximizes 
, and most values of v near 0 produce much larger 
than that of the well-mixed population (solid line). The value of r corresponding to the maximum value of 
varies with v (inset). (d) 
is maintained around a constant value (Nu) with the increase of v irrespective of M. Parameters: (a) v = 0.1, M = 7, N = 100; (b) v = 0.1, M = 7; (c) u = 0.018, M = 7, N = 100; (d) N = 100, r = 1.
We now focus on the effect of migration (probability and range) on 
and 
(Fig. 3). The migration probability or the migration range leads to a significant change of 
and a relatively negligible one of 
. There exists a moderate migration probability maximizing 
, and the majority of migration probabilities near 0 result in much greater values of 
than that of the well-mixed population. The migration range which gives rise to the maximum value of 
varies with the migration probability: it is the longest range 
for very low migration probabilities, intermediate ranges for a little higher but still a small proportion of migration probabilities, and the shortest range (r = 1) for the remaining majority of migration probabilities.
Comparing the Wright-Fisher process with the Moran process
Similar to the Moran process, the parameters σ1 and σ2 of the Wright-Fisher process can be expressed by the probabilities (under neutral selection) assigned to the event that three randomly chosen (without replacement) individuals use given strategies and locations. We obtain such probabilities of the Wright-Fisher process (see Supplementary Information: IV for the detailed calculations) for any mutation patterns and migration patterns following the example of the Moran process31. Applying these probabilities to ‘global mutation’ of our model (see Supplementary Information: V and Methods for the detailed calculations), we have σ1 and σ2 of the Wright-Fisher process which are denoted by 
and 
in the following expressions where 
and 
are abbreviated as 
and 
.
where 
.
The expressions are suitable for any ‘isotropic’ migration patterns (f(x)), non-zero mutation probabilities (u), migration probabilities (v), population sizes (N), and group numbers (M), and have been verified by Monte Carlo simulations in Fig. 4. Additionally, they do not involve the number of strategies (S), which is in line with the previous literature33.
The theoretical values of 
and 
are in agreement with the simulated values.
The solid line describes the theoretical values of 
(a,b) or of 
(c,d), and the square denotes the simulated values of 
(a,b) or of 
(c,d) averaged over 109 − 106 generations (starting to record at generation 106). Parameters: (a,c) v = 0.1, N = 100, M = 19, r = 1; (b,d) u = 0.1, N = 50, M = 9, r = 4.
After simple calculations, we have
Just like the Moran process, the pairwise competition dominates exclusively the multi-strategy selection for extremely low mutation probabilities, and the competition of multiple strategies with equal frequency for sufficiently large populations and mutation probabilities.
For the group-structured population without migration (v = 0) or the well-mixed population,
In the limit N → +∞, we have 
(0th Taylor expansion) which is identical to the Moran process and 
(1st Taylor expansion) indicating that 
is twice 
(of the Moran process). The result is in accordance with the previous literature48, since the expressions of σ1 and σ2 are the same for the Moran and the Wright-Fisher process in the sense that Nu in the former and 2Nu in the latter are denoted by the same symbol when the population is sufficiently large28.
Most findings of the Wright-Fisher process are qualitatively similar to those of the Moran process (Fig. 5). Compared with the well-mixed population, migration (moderate migration probabilities) causes 
to change with the mutation probability u from a decreasing curve to an inverted U-shaped curve, and maintains the increasing trend of 
with u. The previous conjecture33 is verified that 
is far greater than 
when the product of N (population size) and u is large. The mutation probabilities for 
are extremely close to zero, yet those for 
are the remaining vast majority. Migration (probability and range) results in a significant change of 
and a relatively negligible one of 
. There appears a moderate migration probability maximizing 
, and most migration probabilities near 0 lead to much greater values of 
than that of the well-mixed population. The migration range corresponding to the maximum value of 
is from the longest range 
to intermediate ranges to the shortest range (r = 1) as the migration probability increases.
The changing trends of 
and 
.
(a) As u increases, 
decreases for low v and high v (not shown), and exhibits an inverted U-shaped curve for moderate v. 
expands quickly as u increases. For very low u, 
is greater than 
(inset). For a little higher u, is smaller than 
, and the difference will expand quickly as u increases. (b) As u increases, 
expands with a decreasing speed. The change of 
due to r can be neglected. (c) v or r leads to a significant change of 
but a relatively negligible one of 
. A moderate v near 0 maximizes 
, and most values of v near 0 result in much larger 
than that of the well-mixed population (solid line). There may appear a new local peak for 
at v = 1. The value of r corresponding to the maximum value of 
varies with v (inset). (d) 
is maintained around a constant with the increase of v irrespective of M. Parameters: (a) v = 0.1, M = 7, N = 100; (b) v = 0.1, M = 7; (c) u = 0.01, M = 7, N = 100; (d) N = 100, r = 1.
There are two qualitatively distinct ways to change σ1 and σ2 between the Moran and the Wright-Fisher process (Figs 3 and 5). The curve of 
with respect to the migration probability v only has one peak at a low v; and yet in addition to this peak, there may appear a new local peak for 
at v = 1. The value of 
is linearly increasing with respect to the mutation probability, and yet 
is increasing with a decreasing speed. We also quantitatively compare the two processes based on the values of σ1 and σ2 (Fig. 6). The Moran process is more effective in increasing σ1 than the Wright-Fisher process for a vast majority of migration probabilities. The Wright-Fisher process is always more effective in increasing σ2 than the Moran process, which can be seen from the value of 
for v = 0 since 
and 
change very little with the migration probability,
Comparison of the Wright-Fisher and the Moran process.
(a) For extremely low u (u = 0.001), the competition of multiple strategies with equal frequency exerts a negligible influence on the multi-strategy selection (σ2 → 0), and thus we only compare 
with 
. 
is greater than 
for the vast majority of v, and the reverse holds for the remaining few values of v. (b) For high u (u = 0.9), the pairwise competition exerts a tiny influence on the multi-strategy selection compared with the other competition (σ2 ≫ σ1), and therefore we only compare 
with 
. 
is greater than 
for all v. (c) For moderate u (u = 0.01), the two types of competition jointly determine the multi-strategy selection, and thus we compare the two processes based on both σ1 and σ2. The comparison of σ1 here is qualitatively similar to that of σ1 for u = 0.001. The comparison of σ2 here is qualitatively similar to that of σ2 for u = 0.9. Parameters: N = 100, M = 7, r = 1.
Application: Direct reciprocity
We now use the above findings to study the evolution of cooperation under direct reciprocity. Assume that any two individuals of the same group play m rounds of interactions. In any one round, a cooperator brings a benefit b to his opponent at a cost c (b > c > 0), and a defector brings no benefits and pays no costs. Each individual adopts one of three strategies: ALLC (always cooperate) meaning one cooperates in all rounds, ALLD (always defect) meaning one defects in all rounds, and TFT (tit-for-tat) meaning one cooperates in the first round and follows his opponent’s strategy in the previous round. The payoff matrix is given by
From equation (2), the condition for cooperation to be favored over defection (the average frequency of ALLD over the stationary distribution under weak selection, 〈xALLD〉δ→0, satisfies 〈xALLD〉δ→0 ≤ 1/3) is given by
Larger critical cost-to-benefit ratio, (c/b)*, shows that the evolution of cooperation is favored more in the sense that more values of c/b allow natural selection to favor the evolution of cooperation.
The effects of the mutation probability (u), the migration probability (v), the migration range (r), and the repetition round (m) on (c/b)* are qualitatively similar but quantitatively different for the Moran and the Wright-Fisher process (Fig. 7). For large mutation probabilities, σ2 is the key determinant of (c/b)* compared with σ1 since σ2 ≫ σ1. Here, (c/b)* (around 
) does not change much with u (large u in Fig. 7a,c), and it is almost identical for the Moran and the Wright-Fisher process irrespective of m and v (Fig. 7f). For small mutation probabilities, σ1 and σ2 jointly determine (c/b)* since σ1 has a similar size to σ2, and σ1 is the major determinant. Here, (c/b)* changes a lot with u (low u) and its changing trend with respect to u varies with v (Fig. 7a,c): When the migration probability v is small or large, (c/b)* increases with u, because σ1 becomes smaller (decreasing the dependence of the multi-strategy selection on the pairwise competition enhances the evolution of cooperation); When v is moderate, the change of (c/b)* with u is roughly decreasing with the increase of σ1. Meanwhile for small mutation probabilities (Fig. 7e), the Wright-Fisher process leads to greater values of (c/b)* than the Moran process for small and large migration probabilities satisfying 
, and the reverse holds for the remaining majority of migration probabilities satisfying 
. Migration (probability and range) changes σ2 very little and thus the effect of migration on (c/b)* is similar to its effect on σ1 (Fig. 7b,d): There exists a moderate migration probability maximizing (c/b)*; The optimal migration range corresponding to the maximum value of (c/b)* is from the longest to the shortest range as v increases (the advantage of the optimal intermediate range over other ranges is negligible). Larger repetition round (m) increases (c/b)* by enhancing the inherent payoff advantage of TFT and ALLC over ALLD (Fig. 7e,f).
The competition of ALLC, ALLD, TFT.
In the Moran process (a) and the Wright-Fisher process (c), (c/b)* changes very little with u when u is large, but changes a lot with u when u is small. For small u, the changing trend of (c/b)* with u varies with v. In the Moran process (b) and the Wright-Fisher process (d), the effects of v and r on (c/b)* are separately similar to their effects on σ1. In the two processes (e,f) (c/b)* increases with m. For low u = 0.01 (e), the Wright-Fisher process leads to greater (c/b)* than the Moran process for very low v or very high v, and the reverse holds for moderate v. For high u = 0.9 (f), the two processes result in almost identical (c/b)*. Parameters: N = 100, M = 7, r = 1.
Discussion
It has been proved that the strategy selection under weak selection can be expressed by several parameters (including one) independent of the payoff matrix not only for two-person games32,33 but also for multi-person games49. These parameters play a vital role in determining the strategy selection, but are difficult to calculate for general models. For only a few particular models, they have been obtained for two-person and two-strategy games47,50, two-person and multi-strategy games33, and multi-person and two-strategy games51,52. In this paper, we have focused on two-person and multi-strategy games whose strategy selection can be expressed by two parameters σ1 and σ2. We have calculated the accurate values of σ1 and σ2 for the Moran and the Wright-Fisher process in group-structured populations of any finite sizes. In a previous study33, the values of σ1 and σ2 have been given for large populations. The assumption of large population size guarantees that the calculation procedures are the same for the Moran and the Wright-Fisher process when Nu in the former and 2Nu in the latter are denoted by the same symbol. In finite populations, however, the calculations of σ1 and σ2 vary a lot between the two processes. Accordingly, we have separately provided their concrete calculation procedures in Supplementary Information. The key point in the two procedures is how to obtain some special probabilities under neutral selection. The special probabilities of the Moran process have been given by the previous research31 to investigate the evolution of cooperation in populations with two layers of group structure (whose strategy selection cannot be expressed by σ1 and σ2). The special probabilities of the Wright-Fisher process are rigorously obtained for the first time in this work.
The values of σ1 and σ2 we have calculated are appropriate for any migration patterns, mutation probabilities, migration probabilities, population sizes, and group numbers, and have been verified by Monte Carlo simulations. In previous studies33,48, the values of σ1 and σ2 have been obtained for large populations. A recent study47 has suggested the population size suitable for these studies33,48 is related to the mutation probability, the migration probability, and the group number. Our studies can produce their results with the assumptions of ‘global migration’ and large populations. We also have verified the previous conjecture33 that σ2 is far larger than σ1 when the product of the population size and the mutation probability is large. Moreover, we have obtained some new findings for the Moran and the Wright-Fisher process. Compared with the well-mixed population, migration modifies the relationship between σ1 and the mutation probability from a monotonically decreasing curve to an inverted U-shaped curve, and maintains the increasing relationship between σ2 and the mutation probability. The mutation probabilities for σ1 > σ2 (the pairwise competition dominates the multi-strategy selection) are extremely close to zero, and yet those for σ1 ≤ σ2 (the competition of multiple strategies with equal frequency dominates the multi-strategy selection) are the remaining vast majority.
We have studied how migration (probability and range) affects σ1 and σ2, and the following findings hold for the Moran and the Wright-Fisher process. Migration leads to a significant change of σ1 and a relatively negligible one of σ2. There exists a moderate migration probability maximizing σ1. The migration range leading to the largest value of σ1 decreases as v increases. Prior research47 has studied two-person and two-strategy games whose strategy selection can be expressed by a single parameter σ, and has analyzed the effect of migration on σ for the Moran process. The way that migration varies σ1 (of the multi-strategy selection) is similar to how it changes σ (of the two-strategy selection). This is understandable from the known equality33, 
, because migration can barely change σ2. Moreover, based on 
, our results can be used to obtain σ of the Wight-Fisher process and further analyze the influence of migration on σ. Our results are independent of the payoff matrix and can be applied to any concrete game with multiple strategies. In particular, we have determined how migration affects the evolution of cooperation under direct reciprocity by considering the competition of ALLC, ALLD, TFT.
Besides games on islands30 and games in group-structured populations31, games on graphs (a single node only holds one individual at most and individuals can only migrate to empty nodes) have also been used to find what kind of migration can promote the evolution of cooperation53,54,55,56 and maintain the biological diversity57,58. Migration can be envisaged as a way to generate the coevolution of the population structure and individuals’ strategies. Compared with conventional co-evolutionary rules59,60,61, migration here is a very simple rule in which individuals do not have to know any information about the environment, but moderate migration (probabilities) can promote the evolution of cooperation efficiently. This suggests that moderate change of the interactive structure may be the key factor for the evolution of cooperation in the co-evolutionary dynamics.
Nearly all previous studies have only focused on either the Moran or the Wright-Fisher process28,29,30,31,47,48. Here, we have analyzed the distinct roles of the two processes in the multi-strategy selection. The curve of σ1 with respect to the migration probability v has only one peak at a moderate v in the Moran process; yet in addition to this peak, it can have a new local peak at v = 1 in the Wright-Fisher process. The value of σ2 is almost linearly increasing as the mutation probability expands in the Moran process, and yet it is increasing with a decreasing speed in the Wright-Fisher process. The Moran process is more effective in increasing σ1 for the vast majority of migration probabilities and the Wright-Fisher process is always more effective in increasing σ2.
Our model is a variant or a special case of previous models28,29,30, and our calculations of σ1 and σ2 can be extended to the multi-strategy case of these models after proper modifications. In contrast to the stepping-stone model1,2,3,4,5, our model requires that all subpopulations have changeable sizes instead of a fixed and equal size. Our assumption is more realistic and can bring about more interesting phenomena by introducing the typical feature of group-structured populations, ‘the asynchrony in local extinction and recolonization’. Our investigation may provide some insights into the extension of the stepping-stone models. In turn, the newest developments about the stepping-stone models may give us some ideas for analytically studying more complex and realistic models.
Methods
By using the Mutation-Selection analysis (see Supplementary Information: I for the detailed calculations), natural selection favors the evolution of strategy k under weak selection (i.e., the average frequency of strategy k over the stationary distribution under weak selection, 〈xk〉δ→0, is greater than 1/S) if
where Iij is the total number of games that individuals using strategy i play with individuals using strategy j (each game played by two individuals using strategy i is counted twice in computing Iii). Comparing equation (14) with equation (2), we have the general expressions of σ1 and σ2 as
This equation gives us a simple numerical algorithm, in which x1I22 − x1I23, Sx1I23, x1I21 − x1I23 of all steady states are added up to obtain the numerators and the denominators, to perform Monte Carlo simulations.
In our model, the strategy of an individual (say i) is denoted by si (∈{1, 2, …, S}) and his location is indicated by an M-dimensional vector hi whose kth entry is 1 if he is in the kth group and 0 otherwise. Each term in equation (15) can be expressed by the probabilities under neutral selection (δ = 0) assigned to the event that three randomly chosen (without replacement) individuals use given strategies and locations (see Supplementary Information: II for the detailed calculations),
where Pr(s1 = δ1, s2 = δ2, s3 = δ3, h2 · h3 = 1) is the probability that three randomly chosen (without replacement) individuals (say 1, 2, 3) satisfy s1 = δ1, s2 = δ2, s3 = δ3, h2 · h3 = 1.
Note that the equations in ‘Methods’ are appropriate for the Moran and the Wright-Fisher process. The key point in calculating σ1 and σ2 is to obtain Pr(s1 = δ1, s2 = δ2, s3 = δ3, h2 · h3 = 1).
Additional Information
How to cite this article: Zhang, Y. et al. Impact of migration on the multi-strategy selection in finite group-structured populations. Sci. Rep. 6, 35114; doi: 10.1038/srep35114 (2016).
References
Durrett, R. Probability Models for DNA Sequence Evolution. 2nd edn, New York. (Springer Press, 2008).
Matsen, F. A. & Wakeley, J. Convergence to the island-model coalescent process in populations with restricted migration. Genetics 172, 701–708 (2006).
Wilkins, J. F. A separation-of-timescales approach to the coalescent in a continuous population. Genetics 168, 2227–2244 (2004).
Zähle, I., Cox, J. T. & Durrett, R. The stepping stone model. II. Genealogies and the infinite sites model. Ann. Appl. Probab. 15, 671–699 (2005).
Cox, J. T. Intermediate random migration in the two-dimensional stepping stone model. Ann. Appl. Probab. 20, 785–805 (2010).
Nowak, M. A. Five rules for the evolution of cooperation. Science 314, 1560–1563 (2006).
Szabó, G. & Fáth, G. Evolutionary games on graphs. Phys. Rep. 446, 97–216 (2007).
Nowak, M. A., Tarnita, C. E. & Antal, T. Evolutionary dynamics in structured populations. Philos. Trans. R. Soc. B-Biol. Sci. 365, 19–30 (2010).
Szolnoki, A. et al. Cyclic dominance in evolutionary games: a review. J. R. Soc. Interface 11, 20140735 (2014).
Rand, D. G. & Nowak, M. A. Human cooperation. Trends Cogn. Sci. 17, 413–425 (2013).
Chen, X. J., Zhang, Y. L., Huang, T. Z. & Perc, M. Solving the collective-risk social dilemma with risky assets in well-mixed and structured populations. Phys. Rev. E 90, 052823 (2014).
Perc, M. & Szolnoki, A. Self-organization of punishment in structured populations. New J. Phys. 14, 043013 (2012).
Li, K., Szolnoki, A., Cong, R. & Wang, L. The coevolution of overconfidence and bluffing in the resource competition game. Sci. Rep. 6, 21104 (2016).
Szabó, G. & Király, B. Extension of a spatial evolutionary coordination game with neutral options. Phys. Rev. E 93, 052108 (2016).
Wu, T., Fu, F., Zhang, Y. L. & Wang, L. Adaptive role switching promotes fairness in networked ultimatum game. Sci. Rep. 3, 1550 (2013).
Szolnoki, A. & Perc, M. Evolution of extortion in structured populations. Phys. Rev. E 89, 022804 (2014).
Gavrilets, S. Collective action problem in heterogeneous groups. Phil. Trans. R. Soc. B 370, 20150016 (2015).
Perc, M., Gómez-Gardeñes, J., Szolnoki, A., Floría, L. M. & Moreno, Y. Evolutionary dynamics of group interactions on structured populations: a review. J. R. Soc. Interface 10, 20120997 (2013).
Masuda, N. & Fu, F. Evolutionary models of in-group favoritism. F1000Prime Reports 7, 27 (2015).
Killingback, T., Bieri, J. & Flatt, T. Evolution in group-structured populations can resolve the tragedy of the commons. Proc. R. Soc. B-Biol. Sci. 273, 1477–1481 (2006).
Li, A. M., Broom, M., Du, J. M. & Wang, L. Evolutionary dynamics of general group interactions in structured populations. Phys. Rev. E. 93, 022407 (2016).
Hauert, C. & Imhof, L. A. Evolutionary games in deme structured, finite populations. J. Theor. Biol. 299, 106–112 (2012).
Gao, S. P., Wu, T., Nie, S. L. & Wang, L. Emergence of parochial altruism in well-mixed populations of multiple groups. Phys. Lett. A 379, 2311–2318 (2015).
Masuda, N. Evolution via imitation among like-minded individuals. J. Theor. Biol. 349, 100–108 (2014).
Girvan, M. & Newman, M. E. J. Community structure in social and biological networks. Proc. Natl. Acad. Sci. USA 99, 7821–7826 (2002).
Mund, A., Kuttler, C., Pérez-Velázquez, J. & Hense, B. A. An age-dependent model to analyse the evolutionary stability of bacterial quorum sensing. J. Theor. Biol. 405, 104–115 (2016).
Fu, F., Tarnita, C. E., Christakis, N. A., Wang, L., Rand, D. G. & Nowak, M. A. Evolution of in-group favoritism. Sci. Rep. 2, 460 (2012).
Antal, T., Ohtsuki, H., Wakeley, J., Taylor, P. D. & Nowak, M. A. Evolution of cooperation by phenotypic similarity. Proc. Natl. Acad. Sci. USA 106, 8597–8600 (2009).
Tarnita, C. E., Antal, T., Ohtsuki, H. & Nowak, M. A. Evolutionary dynamics in set structured populations. Proc. Natl. Acad. Sci. USA 106, 8601–8604 (2009).
Fu, F. & Nowak, M. A. Global migration can lead to stronger spatial selection than local migration. J. Stat. Phys. 151, 637–653 (2013).
Zhang, Y. L., Fu, F., Chen, X. J., Xie, G. M. & Wang, L. Cooperation in group-structured populations with two layers of interactions. Sci. Rep. 5, 17446 (2015).
Tarnita, C. E., Ohtsuki, H., Antal, T., Fu, F. & Nowak, M. A. Strategy selection in structured populations. J. Theor. Biol. 259, 570–581 (2009).
Tarnita, C. E., Wage, N. & Nowak, M. A. Multiple strategies in structured populations. Proc. Natl. Acad. Sci. USA 108, 2334–2337 (2011).
Nowak, M. A., Sasaki, A., Taylor, C. & Fudenberg, D. Emergence of cooperation and evolutionary stability in finite populations. Nature 428, 646–650 (2004).
Zhang, Y. L., Fu, F., Wu, T., Xie, G. M. & Wang, L. Inertia in strategy switching transforms the strategy evolution. Phys. Rev. E. 84, 066103 (2011).
Ohtsuki, H., Hauert, C., Lieberman, E. & Nowak, M. A. A simple rule for the evolution of cooperation on graphs and social networks. Nature 441, 502–505 (2006).
Du, J. M., Wu, B. & Wang, L. Aspiration dynamics in structured population acts as if in a well-mixed one. Sci. Rep. 5, 8014 (2015).
Rand, D. G., Tarnita, C. E., Ohtsuki, H. & Nowak, M. A. Evolution of fairness in the one-shot anonymous ultimatum game. Proc. Natl. Acad. Sci. USA 110, 2581–2586 (2013).
Wu, B., Altrock, P. M., Wang, L. & Traulsen, A. Universality of weak selection. Phys. Rev. E. 82, 046106 (2010).
Allen, B. & Nowak, M. A. Games among relatives revisited. J. Theor. Biol. 378, 103–116 (2015).
Gao, S. P., Wu, T., Nie, S. L. & Wang, L. Promote or hinder? The role of punishment in the emergence of cooperation. J. Theor. Biol. 386, 69–77 (2015).
Traulsen, A. & Nowak, M. A. Evolution of cooperation by multilevel selection. Proc. Natl. Acad. Sci. USA 103, 10952–10955 (2006).
Wu, B., García, J., Hauert, C. & Traulsen, A. Extrapolating weak selection in evolutionary games. PLoS Comput. Biol. 9, e1003381 (2013).
Wu, B., Bauer, B., Galla, T. & Traulsen, A. Fitness-based models and pairwise comparison models of evolutionary games are typically different-even in unstructured populations. New J. Phys. 17, 023043 (2015).
Allen, B., Nowak, M. A. & Dieckmann, U. Adaptive dynamics with interaction structure. Am. Nat. 181, E139–E163 (2013).
Sasaki, T. & Okada, I. Cheating is evolutionarily assimilated with cooperation in the continuous snowdrift game. Biosystems 131, 51–59 (2015).
Zhang, Y. L., Su, Q. & Cun, C. Y. Intermediate-range migration furnishes a narrow margin of efficiency in the two-strategy competition. PLoS ONE 11, e0155787 (2016).
Antal, T., Traulsen, A., Ohtsuki, H., Tarnita, C. E. & Nowak, M. A. Mutation-selection equilibrium in games with multiple strategies. J. Theor. Biol. 258, 614–622 (2009).
McAvoy, A. & Hauert, C. Structure coefficients and strategy selection in multiplayer games. J. Math. Biol. 72, 203–238 (2016).
Nathanson, C. G., Tarnita, C. E. & Nowak, M. A. Calculating evolutionary dynamics in structured populations. PLoS Comput. Biol. 5, e1000615 (2009).
Peña, J., Wu, B., Arranz, J. & Traulsen, A. Evolution of multiplayer cooperation on graphs. PLoS Comput. Biol. 12, e1005059 (2016).
Wu, B., Traulsen, A. & Gokhale, C. S. Dynamic properties of evolutionary multi-player games in finite populations. Games 4, 182–199 (2013).
Cong, R., Wu, B., Qiu, Y. & Wang, L. Evolution of cooperation driven by reputation-based migration. PLoS ONE 7, 35776 (2012).
Wu, T., Fu, F., Zhang, Y. L. & Wang, L. Expectation-driven migration promotes cooperation by group interactions. Phys. Rev. E 85, 066104 (2012).
Helbing, D. & Yu, W. The outbreak of cooperation among success-driven individuals under noisy conditions. Proc. Natl. Acad. Sci. USA 106, 3680–3685 (2009).
Chen, X. J., Szolnoki, A. & Perc, M. Risk-driven migration and the collective-risk social dilemma. Phys. Rev. E 86, 036101 (2012).
Reichenbach, T., Mobilia, M. & Frey, E. Mobility promotes and jeopardizes biodiversity in rock-paperscissors games. Nature 448, 1046–1049 (2007).
Szolnoki, A. & Perc, M. Zealots tame oscillations in the spatial rock-paper-scissors game. Phys. Rev. E 93, 062307 (2016).
Rong, Z., Wu, Z. X. & Chen, G. Coevolution of strategy-selection time scale and cooperation in spatial prisoners dilemma game. Europhys. Lett. 102, 68005 (2013).
Wu, B., Arranz, J., Du, J., Zhou, D. & Traulsen, A. Evolving synergetic interactions. J. R. Soc. Interface 13, 20160282 (2016).
Perc, M. & Szolnoki, A. Coevolutionary games-a mini review. Biosystems 99, 109–125 (2010).
Acknowledgements
We are grateful for support by the Fundamental Research Funds for the Central Universities (No. FRF-TP-15-116A1), the China Postdoctoral Science Foundation (No. 2015M580989), and the National Natural Science Foundation of China (No. 61520106009, No. 61533008).
Author information
Authors and Affiliations
Contributions
Y.Z. conceived the model and wrote the paper. Y.Z. and A.L. performed analyses. Y.Z. and C.S. discussed the results and revised the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Zhang, Y., Liu, A. & Sun, C. Impact of migration on the multi-strategy selection in finite group-structured populations. Sci Rep 6, 35114 (2016). https://doi.org/10.1038/srep35114
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep35114
This article is cited by
-
State Feedback Control Promotes Transition Efficiency of Bag Filters
International Journal of Control, Automation and Systems (2024)
-
Individual mobility promotes punishment in evolutionary public goods games
Scientific Reports (2017)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.
