Abstract
The spin-torque driven dynamics of antiferromagnets with Dzyaloshinskii-Moriya interaction (DMI) were investigated based on the Landau-Lifshitz-Gilbert-Slonczewski equation with antiferromagnetic and ferromagnetic order parameters (l and m, respectively). We demonstrate that antiferromagnets including DMI can be described by a 2-dimensional pendulum model of l. Because m is coupled with l, together with DMI and exchange energy, close examination of m provides fundamental understanding of its dynamics in linear and nonlinear regimes. Furthermore, we discuss magnetization reversal as a function of DMI and anisotropy energy induced by a spin current pulse.
Similar content being viewed by others
Introduction
Since the first discovery of sub-picosecond demagnetization of ferromagnetic nickel film using femtosecond infrared lasers, ultrafast manipulation of magnetization has raised much interest in terms of both condensed matter physics and applications in information storage devices1. Together with the development of femtosecond lasers, a considerable number of research studies have been conducted to explore the microscopic dynamics experimentally as well as theoretically for various magnetic systems2,3,4,5,6,7,8,9,10,11,12,13.
The antiferromagnet (AF) system is a promising structure for ultrafast processes because it has a relatively strong exchange interaction that shifts the precession frequency into the terahertz range. The AF system can be excited or switched at picosecond timescales (significantly faster than ferromagnetic precession14,15,16,17), and AF switching through current-induced spin transfer torque has been recently measured electrically18.
AF systems with weak ferromagnetism (AWF) might be useful for memory devices because of their weak ferromagnetism and selectively controllable excitation modes19. The weak ferromagnetism is associated with broken inversion symmetry in the material and is independent of any ferromagnetic impurities20. This type of magnetism has been studied experimentally in the rare earth orthoferrites21,22,23,24,25,26 and rhombohedral antiferromagnet FeBO327,28 by many research groups. However, analytical approaches to describe AWF dynamics are rare except for AF cases15,29.
This paper shows that AWF dynamics is governed by the classical pendulum equations on the antiferromagnetic order parameter (l), similar to the simple AF case14. We demonstrate quantitatively that the occurrence of the second harmonic of the ferromagnetic order parameter (m) is direct evidence for a nonlinear regime, including resonant frequency softening30, and that the ellipticity of the precessional motion of m determines the Dzyaloshinskii-Moriya interaction (DMI) energy. Additionally, we propose that sub-lattice dynamics (s1, s2) can be revealed experimentally. We discuss switching efficiency as a function of anisotropy, DMI energy and damping constant (α) using spin current pulse with various durations and densities.
Theory
AWF dynamics
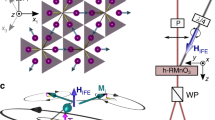
Figure 1 shows AWF static and dynamic configurations based on two sub-lattice models below the Néel temperature31. Antiferromagnetically coupled spins lie along the x-axis because the anisotropy of the spins occurs along the uniaxial direction, with the magnetic easy axis parallel to x-axis, and the spins are tilted along the z-axis due to the DMI vector,  , as shown in Fig. 1(a). The DMI produces two resonant modes, called the Sigma mode and the Gamma mode (S- and G-mode, respectively)19.
, as shown in Fig. 1(a). The DMI produces two resonant modes, called the Sigma mode and the Gamma mode (S- and G-mode, respectively)19.
(a) Schematic diagram for an antiferromagnet with Dzyaloshinskii-Moriya interaction at T < TN. The ferromagnetic order parameter, m, and the antiferromagnetic order parameter, l, are defined as (s1 + s2)/2 and (s1 − s2)/2, respectively. m is exaggerated compared to l. Inset shows the DM interaction mechanism between the sub-lattices and oxygen. Two resonant modes are selectively excited depending on the injected spin polarization: Sigma mode in p|| (b) and Gamma mode in p||
(b) and Gamma mode in p|| (c). (d,e) are reproductions of (b,c), respectively, in terms of l and m.
(c). (d,e) are reproductions of (b,c), respectively, in terms of l and m.
Landau-Lifshitz-Gilbert-Slonczewski equation
To better understand the kinetics of AWF, the total energy based on two sub-lattices with i = 1, 2 is expressed as

where the normalized magnetization, si = Si/S0 with S0 = |Si| is dimensionless, and ħ is the reduced Plank constant. The first term is related to the exchange energy, where J is the nearest-neighbor symmetric exchange constant, with the positive sign accounting for AF coupling. The second term describes Dzyaloshinskii-Moriya (DM) energy, where the DM vector, D, is  , Dy > 0, and its magnitude is relatively weak. The third and fourth terms are anisotropy energies where anisotropy constants are Kx > 0 and Kz < 0, indicating magnetic in-plane and out-of-plane anisotropy, respectively. These energy combinations cause the anti-parallel spins to be tilted slightly along the z-axis. The dynamics can be described by the coupled Landau-Lifshitz-Gilbert-Slonczewski equation of motion:
, Dy > 0, and its magnitude is relatively weak. The third and fourth terms are anisotropy energies where anisotropy constants are Kx > 0 and Kz < 0, indicating magnetic in-plane and out-of-plane anisotropy, respectively. These energy combinations cause the anti-parallel spins to be tilted slightly along the z-axis. The dynamics can be described by the coupled Landau-Lifshitz-Gilbert-Slonczewski equation of motion:

The fifth term is phenomenological damping, which is characterized by the Gilbert damping constant (α). The final term is the Slonczewski-type spin transfer torque (STT), where p is the unit vector of spin polarization, and Ω is the STT strength with angular frequency unit, defined as εħγJs/(2VS0e), which is proportional to the spin current density, Js, where ε and V are the scattering efficiency and volume of AWF region, respectively14,29,32.
We use staggered magnetization, l = (s1 − s2)/2, and weak magnetization, m = (s1 + s2)/2, so that Eq. (2) becomes


where Damping and STT are α(m × l + l × m) and Ω[m × (l × p) + l × (m × p)], respectively. Equations (3) and (4) are constrained by

Consider the S-mode excited by spin current with polarization, p|| . When the STT turns on, s1 and s2 are dragged slightly toward the y-axis by the exchange coupling between the conduction electrons and the magnetic moments, as shown in Fig. 1(b). Consequently, as my increases in magnitude, l is moved away from its equilibrium position. After the STT turns off, l and m are subject to an internal magnetic field torque, and m precesses on the xy-plane and fluctuates along the z-axis, as shown in Fig. 1(d). (In a simple AF, only my fluctuation is shown14,17,29.) This is ascribed to the DMI, coupled with mx and mz, which causes elliptical polarization of precessional motion ofm, as shown in Fig. 1(d). The details are discussed below, in conjunction with the second harmonic oscillation of mz.
. When the STT turns on, s1 and s2 are dragged slightly toward the y-axis by the exchange coupling between the conduction electrons and the magnetic moments, as shown in Fig. 1(b). Consequently, as my increases in magnitude, l is moved away from its equilibrium position. After the STT turns off, l and m are subject to an internal magnetic field torque, and m precesses on the xy-plane and fluctuates along the z-axis, as shown in Fig. 1(d). (In a simple AF, only my fluctuation is shown14,17,29.) This is ascribed to the DMI, coupled with mx and mz, which causes elliptical polarization of precessional motion ofm, as shown in Fig. 1(d). The details are discussed below, in conjunction with the second harmonic oscillation of mz.
Because the ly component is much smaller than lx and lz, the dynamics of lcan be regarded as approximately 2-dimensional (2D) pendulum motion oscillating with angle φ1 on the xz-plane (see Supplementary information). Therefore, we expand Eqs (3) and (4) by using the effective vectors (lx, 0, lz) and (0, my, 0), and take the cross product of l on Eq. (4) to extract only m,


where the equations are simplified by employing Eq. (5) and ignoring terms coupled with anisotropy energy because |Kx| and |Kz| ≪ Dy and J. Substituting Eq. (7) into Eq. (3), we have the 2D pendulum equations,

where  .
.
In G-mode, p|| ; thus, s1 and s2 are dragged slightly toward the z-axis, as shown in Fig. 1(c). As mz increases in magnitude, with mx and my remaining zero, l is moved away from the equilibrium position (see Supplementary information). After STT turns off, mz shows only fluctuation motion and loscillates on the xy-plane, as shown in Fig. 1(e). The methodology in S-mode is used again, so that
; thus, s1 and s2 are dragged slightly toward the z-axis, as shown in Fig. 1(c). As mz increases in magnitude, with mx and my remaining zero, l is moved away from the equilibrium position (see Supplementary information). After STT turns off, mz shows only fluctuation motion and loscillates on the xy-plane, as shown in Fig. 1(e). The methodology in S-mode is used again, so that


Substituting Eq. (9) into Eq. (3), the 2D pendulum equation becomes

where  , with spin canting angle β in equilibrium (l and lz = 0) because tan[β] = mz/lx = Dy/(2J). These outcomes confirm White et al.19.
, with spin canting angle β in equilibrium (l and lz = 0) because tan[β] = mz/lx = Dy/(2J). These outcomes confirm White et al.19.
Results and Discussion
Ultrafast dynamics in the terahertz regime
We introduce the DMI or antisymmetric super-exchange interaction from the triangle spanned among three ions (magnetic ions and oxygen ion). Such an interaction was discovered in the interface between AF and ferromagnet33, and between AF and ferrimagnet superlattices34, as well as bulk crystals20,21,22,23,24,25,26. Here, we suppose a two-layer system consisting of two antiferromagnetic oxides, where the interaction between two magnetic ions arranged along the x-axis, and the oxygen ion, shifted slightly to the z-axis, gives rise to DM vector, , as shown in the inset of Fig. 1(a). Because the magnetic easy axis is the x-axis, sub-lattice spins are canted toward the z-axis. Additionally, we assume that the magnetic unit cell exhibits weak ferromagnetism, as in the case of rare earth ferrite, ReFeO3 single crystal (Re: Er, Tm, and Y, etc). The parameters chosen were J = 113.5 meV, Kx = 4.14 μeV, Kz = 0, and Dy = 0.01J so that spin precession motion is in the terahertz frequency range. To inject spin current into AWF, we exploit the spin hall effect in Pt with strong spin-orbit coupling. Figure 2(a,b) show S-mode and G-mode in AWF (see Supplementary Movie 1 & 2). Moreover, we checked that our analytical results are validated by numerical calculations based on Eq. (1) (see Supplementary Figure 2 and 3). However, for stronger DM energy, we found that the analytical solution deviates from the numerical one because the approximation (
, as shown in the inset of Fig. 1(a). Because the magnetic easy axis is the x-axis, sub-lattice spins are canted toward the z-axis. Additionally, we assume that the magnetic unit cell exhibits weak ferromagnetism, as in the case of rare earth ferrite, ReFeO3 single crystal (Re: Er, Tm, and Y, etc). The parameters chosen were J = 113.5 meV, Kx = 4.14 μeV, Kz = 0, and Dy = 0.01J so that spin precession motion is in the terahertz frequency range. To inject spin current into AWF, we exploit the spin hall effect in Pt with strong spin-orbit coupling. Figure 2(a,b) show S-mode and G-mode in AWF (see Supplementary Movie 1 & 2). Moreover, we checked that our analytical results are validated by numerical calculations based on Eq. (1) (see Supplementary Figure 2 and 3). However, for stronger DM energy, we found that the analytical solution deviates from the numerical one because the approximation ( ) is no longer valid. (see Supplementary information).
) is no longer valid. (see Supplementary information).
Excitation modes when (a) p|| and Ω = 0.8 GHz and (d) p||
and Ω = 0.8 GHz and (d) p|| and Ω = 0.5 GHz. Spin trajectories (left) and spectra (right) are shown in fourth row. In both cases, the pulse duration (τ) is 1 ps and the Gilbert damping constant is 0 (see Supplementary Movie 1 and 2).
and Ω = 0.5 GHz. Spin trajectories (left) and spectra (right) are shown in fourth row. In both cases, the pulse duration (τ) is 1 ps and the Gilbert damping constant is 0 (see Supplementary Movie 1 and 2).
Second harmonic oscillation of Mz as a nonlinear effect
S- and G-mode dynamics have common characteristic motion: second harmonic oscillations along the z-axis. According to Eqs (6) and (9),  and
and  are both responsible for the nonlinearity of lx, together with the resonant frequency softening30. For example, φ1(t) is sinusoidal in Ω = 0.8 GHz; as a results, mz = lx · Dy/ħ ∼ cos[φ1(t)] = cos[Asin[ωSigmat]] is replaced with ~(1 − A2/4) − A2cos[2ωSigmat]/4 by its first order Taylor expansion. Likewise,
are both responsible for the nonlinearity of lx, together with the resonant frequency softening30. For example, φ1(t) is sinusoidal in Ω = 0.8 GHz; as a results, mz = lx · Dy/ħ ∼ cos[φ1(t)] = cos[Asin[ωSigmat]] is replaced with ~(1 − A2/4) − A2cos[2ωSigmat]/4 by its first order Taylor expansion. Likewise,  and
and  are shown in Fig. 2(a,b), fourth row, right.
are shown in Fig. 2(a,b), fourth row, right.
Determination of DMI strength
The DMI strength can be obtained by examining the first harmonic precession on the xy-plane in the S-mode,  . Using Eqs (6) and (7), the ellipticity, ε is calculated as my(t)/mx(t) = [−2J/(Dylz)] ħ(
. Using Eqs (6) and (7), the ellipticity, ε is calculated as my(t)/mx(t) = [−2J/(Dylz)] ħ( )/(2J)] = AħωSigmacos[ωSigmat]/(Dysin[Asin[ωSigmat]]). If we assume A is small enough, ε
)/(2J)] = AħωSigmacos[ωSigmat]/(Dysin[Asin[ωSigmat]]). If we assume A is small enough, ε . For example,
. For example,  is constant within a few percent with
is constant within a few percent with  , as shown in Fig. 2(a), fourth row, left. Experimentally, the precessional polarization in S-mode can be measured using optical tools: terahertz time domain spectroscopy23,24,25,26,27,28,30, or time resolved magneto optical Kerr/Faraday rotation16,21,22.
, as shown in Fig. 2(a), fourth row, left. Experimentally, the precessional polarization in S-mode can be measured using optical tools: terahertz time domain spectroscopy23,24,25,26,27,28,30, or time resolved magneto optical Kerr/Faraday rotation16,21,22.
s1 and s2 deduced from m and l
Once the DMI strength is determined, J is easily estimated by using well-known antisymmetric exchange model, Ms ∼ M0Dy/(2J)35, where saturation magnetization, Ms can be measured by using a conventional sample vibrating magnetometer. M0 is the number of magnetic ions per volume or mole. Conventional time domain terahertz spectroscopy (or time resolved magneto optical Kerr/Faraday rotation technique) can be used to observe m(t). From the Fourier transform of mx(t) (or my(t)) and mz(t), the resonant frequencies (and thereby Kx and Kz) are obtained. As m, D, and J are determined, l could be estimated using Eqs (6) and (9). For example, in S-mode, lz and lx can be deduced from mxand mz using Eqs (5) and (6). In G-mode, lx and lz can be estimated using Eqs (8) and (9) and the spectral amplitude and phase information. The resulting s1 and s2 are shown in Fig. 1(b,c). In contrast, lx is not extractable in simple AF because of the lack of DMI14.
Switching mechanism and efficiency
Figure 3(a,b) show the switching process for S-mode and G-mode, respectively (see Supplementary Movie 3 and 4). In S-mode, |m|, defined as  , (or mz in G-mode), increases in magnitude less than 1% for |lmax| ~ 1 with the spin current pulse. Additional canting is converted into kinetic energy, and if the kinetic energy exceeds the maximum potential energy, spin reversal occurs after the pulse has been turned off. This is inertia-driven switching17, and the switching is identically applied in G-mode.
, (or mz in G-mode), increases in magnitude less than 1% for |lmax| ~ 1 with the spin current pulse. Additional canting is converted into kinetic energy, and if the kinetic energy exceeds the maximum potential energy, spin reversal occurs after the pulse has been turned off. This is inertia-driven switching17, and the switching is identically applied in G-mode.
Magnetization switching when (a) p|| and Ω = 6.2 GHz and (b) p||
and Ω = 6.2 GHz and (b) p|| and Ω = 9 GHz. In both cases, the pulse duration (τ) is 1 ps and the Gilbert damping constant is 0.0005 (see Supplementary Movie 3 and 4).
and Ω = 9 GHz. In both cases, the pulse duration (τ) is 1 ps and the Gilbert damping constant is 0.0005 (see Supplementary Movie 3 and 4).
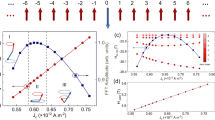
Because either ωSigma or ωGamma could be manipulated by Kz or Dy, switching efficiency should be considered for these parameters. Figure 4 shows the periodic patterns for the terminal phase of lx for various values of Kx and Dy after excitation by spin current pulses for several values of τ, Ω and p. From left down to right up, terminal phases of lx are indicated by nπ, n = 0, 1, 2.
(a–c,f) Periodic patterns of terminal phase of lx for various conditions of Kx, Kz, Dy, and p in the Ω versus τ plot after excitation by a pulsed spin current. From left down to right up, the terminal phases of lx are indicated by nπ, n = 0, 1, 2, … (even = yellow, odd = black), α = 0.01. (d–e) Potential energy distribution with Kz = 0, Kz = −0.5 Kx, and Kx = 4.14 μeV.
When the potential barrier increases from Kz = 0 in Fig. 4(d) to Kz = −0.5|Kx| in Fig. 4(e), l in S-mode must overcome the higher potential barrier on the xz-plane. Thus, phases of lx are shifted upward in Fig. 4(b), compared to Fig. 4(a). Another factor to modify the switching efficiency is the DMI strength in G-mode, where Kz does not play a role in the control of the energy barrier on the xy-plane because the energy barrier on the xz-plane is controllable by Kz. When Dy = 0.01 J in Fig. 4(c), the pendulum system energy is higher than that of Dy = 0.005 J in Fig. 4(f), and the first switching demands higher STT strength. Experimentally, magnetic materials have temperature dependence on anisotropy energies or thickness dependence on Dy33,36. Additionally, the interface engineering is used to change DMI strength37. Applying these properties, one can expect to switch magnetization under optimal conditions. In particular, AWF systems, which have anisotropy with two easy-axes (Kx and Kz > 0), would undergo switching at a lower critical STT strength (Ωc) in S-mode, because Kz lowers the switching barrier. Finally, we checked the α dependence. When the pulse duration (τ) is short, the damping effect obviously lowers Ωc: For example, Ωc = 4.4 GHz, τ = 5 ps for α = 0.007 and Ωc = 3.8 GHz, τ = 5 ps for α = 0.005 in Fig. 5(a,b). In general, as α becomes smaller, the periodic patterns become narrower14. In particular, in short τ, the slope of the phase boundary is steep and dependent on α; thus, one might doubt its stable functionality as a device. In long τ, Ωc is much reduced and finally become minimized, but its magnitude is not further reduced for variation of α.
Conclusion
In summary, we investigated the process of precession motion in antiferromagnets with weak ferromagnetism through spin transfer torque. Although DMI splits the AF resonant mode into S- and G-modes, the modes are also be interpreted as pendulum models on l. Because l and DMI energy are coupled and independently extractable through measurement of m, dynamic analysis of m provides fundamental understanding of sub-lattice dynamics, as shown in Fig. 1(b,c). Adjustment of appropriate parameters, such as the anisotropy barrier and DMI strength, provide more efficient magnetization reversal.
Additional Information
How to cite this article: Kim, T. H. et al. Ultrafast spin dynamics and switching via spin transfer torque in antiferromagnets with weak ferromagnetism. Sci. Rep. 6, 35077; doi: 10.1038/srep35077 (2016).
References
Beaurepaire, E., Merle, J.-C., Daunois, A. & Bigot, J.-Y. Ultrafast spin dynamics in ferromagnetic Nickel. Phys. Rev. Lett. 76, 4250 (1996).
Kirilyuk, A., Kimel, A. V. & Rasing, Th. Ultrafast optical manipulation of magnetic order. Rev. Mod. Phys. 82, 2731–2784 (2010).
Stanciu, C. D. et al. All-optical magnetic recording with circularly polarized light. Phys. Rev. Lett. 99, 047601 (2007).
Koopmans, B., van Kampen, M., Kohlhepp, J. T. & de Jonge, W. J. M. Ultrafast magneto-optics in nickel: Magnetism or Optics? Phys. Rev. Lett. 85, 844–847 (2000).
Guidoni, L., Beaurepaire, E. & Bigot, J.-Y. Magneto-optics in the ultrafast regime: Thermalization of Spin Populations in Ferromagnetic Films. Phys. Rev. Lett. 89, 017401 (2002).
Zhang, G. P., Hubner, W., Lefkidis, G., Bai, Y. & George, T. F. Paradigm of the time-resolved magneto-optical Kerr effect for femtosecond magnetism. Nature Phys. 5, 499–502 (2009).
Carva, K., Battiatio, M. & Oppeneer, P. M. Is the controversy over femtosecond magneto-optics really solved? Nature Phys. 7, 665–666 (2011).
Malinowski, G. et al. Control of speed and efficiency of ultrafast demagnetization by direct transfer of spin angular momentum. Nature Phys. 4, 855–858 (2008).
Bigot, J.-Y., Vomir, M. & Beaurepaire, E. Coherent ultrafast magnetism induced by femtosecond laser pulses. Nature Phys. 5, 515–520 (2009).
Zhang, G. P., Bai, Y. & George, T. F. Energy- and crystal momentum-resolved study of laser-induced femtosecond magnetism. Phys. Rev. B 80, 214415 (2009).
Koopmans, B. et al. Magnetization dynamics: Ferromagnets stirred up. Nature Mater. 9, 259–265 (2010).
Battiato, M., Carva, K. & Oppeneer, P. M. Superdiffusive spin transport as a mechanism of ultrafast demagnetization. Phys. Rev. Lett. 105, 027203 (2010).
Fähnle, M. & Illg, C. Electron theory of fast and ultrafast dissipative magnetization dynamics. J. Phys. Condens. Matter 23, 493201 (2011).
Cheng, R., Daniels, M. W., Zhu, J. G. & Xiao, D. Ultrafast switching of antiferromagnets via spin-transfer torque. Phys. Rev. B 91, 064423 (2015).
Cheng, R., Xiao, J., Niu, Q. & Brataas, A. Spin pumping and spin-transfer torques in Antiferromagnets. Phys. Rev. Lett. 113, 057601 (2014).
Kampfrath, T. et al. Coherent terahertz control of antiferromagnetic spin waves. Nat. Photonics 5, 31 (2011).
Wienholdt, S., Hinzke, D. & Nowak, U. THz switching of antiferromagnets and ferrimagnets. Phys. Rev. Lett. 108, 247207 (2012).
Wadley, P. et al. Electrical switching of an antiferromagnet. Science 351, 587 (2016)
White, R. M., Nemanich, R. J. & Herring, C. Light scattering from magnetic excitations in orthoferrites. Phys. Rev. B 25, 1822 (1982).
Dzyaloshinsky, I. A thermodynamic theory of weak ferromagnetism of antiferromagnetics. J. Phys. Chem. Solids 4, 241–255 (1958).
Kimel, A. V. et al. Ultrafast non-thermal control of magnetization by instantaneous photomagnetic pulses. Nature 435, 655 (2005).
Kimel, A. V. et al. Inertia-driven spin switching in antiferromagnets. Nature Phys. 5, 727 (2009).
Kim, T. H. et al. Coherently controlled spin precession in canted antiferromagnetic YFeO3 using terahertz magnetic field. Appl. Phys. Express 7, 093007 (2014).
Mikhaylovskiy, R. V. et al. Terahertz emission spectroscopy of laser-induced spin dynamics in TmFeO3 and ErFeO3 orthoferrites. Phys. Rev. B 90, 184405 (2014).
Kim, T. H. et al. Magnetization states of canted antiferromagnetic YFeO3 investigated by terahertz time-domain spectroscopy. J. Appl. Phys. 118. 233101 (2015).
Mikhaylovskiy, R. V. et al. Terahertz magnetization dynamics induced by femtosecond resonant pumping of Dy3+ subsystem in the multisublattice antiferromagnet DyFeO3 . Phys. Rev. B 92, 094437 (2015).
Mikhaylovskiy, R. V. et al. Ultrafast optical modification of exchange interactions in iron oxides. Nat. Commun. 6, 8190 (2015).
Huisman, T. J., Mikhaylovskiy, R. V., Tsukamoto, A., Rasing, Th. & Kimel, A. V. Simultaneous measurements of terahertz emission and magneto-optical Kerr effect for resolving ultrafast laser-induced demagnetization dynamics. Phys. Rev. B 92, 104419 (2015).
Gomonay, H. V. & Loktev, V. M. Spin transfer and current-induced switching in antiferromagnets. Phys. Rev. B 81, 144427 (2010).
Mukai, Y., Hirori, H., Yamamoto, T., Kageyama, H. & Tanaka, K. Nonlinear magnetization dynamics of antiferromagnetic spin resonance induced by intense terahertz magnetic field. New J. Phys. 18 013045 (2016).
Kocharyan, K. N., Martirosyan, R. M., Prpryan, V. G. & Sarkisyan, E. L. Faraday effect in yttrium orthoferrite in the “low-frequency” antiferromagnetic resonance region. Sov. Phys. JETP 59, 373 (1984).
Slonczewski, J. C. Current-driven excitation of magnetic multilayers. J. Magn. Magn. Mater. 159, 1 (1996).
Dong et al. Exchange Bias Driven by the Dzyaloshinskii-Moriya Interaction and Ferroelectric Polarization at G-Type Antiferromagnetic Perovskite Interfaces. Phys. Rev, Lett. 103, 127201 (2009).
Ijiri, Y., Schulthess, T. C., Borchers, J. A., van der Zaag, P. J. & Erwin, R. W. Perpendicular Coupling in Exchange-Biased Fe3O4/CoO Superlattices. Phys. Rev, Lett. 99, 147201 (2007).
Gorodetsky, G. & Treves, D. Second-Order Susceptibility Terms in Orthorferrites at Room temperature. Phys. Rev. 135, A97 (1964).
Cho, J. et al. Thickness dependence of the interfacial Dzyaloshinskii–Moriya interaction in inversion symmetry broken systems. Nat. Commun. 6, 7635 (2015).
Chen, G. et al. Tailoring the chirality of magnetic domain walls by interface engineering. Nat. Commun. 4, 2671 (2013).
Acknowledgements
This work was supported by the National Research Foundation of Korea (NRF) grants funded by the Ministry of Science, ICT and Future Planning (MSIP) of Korea (Bank for Quantum Electronic Materials, No. 2011-0028736 and 2013K000315).
Author information
Authors and Affiliations
Contributions
B.C. and T.H.K. conceived the project idea and planned the analytical and numerical calculations. T.H.K. performed the analytical and numerical calculations. T.H.K., P.G., S.H.H. and B.C. analyzed the data. B.C. led the work and wrote the manuscript with T.H.K. The results of the theoretical and numerical findings were discussed by all coauthors.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Kim, T., Grünberg, P., Han, S. et al. Ultrafast spin dynamics and switching via spin transfer torque in antiferromagnets with weak ferromagnetism. Sci Rep 6, 35077 (2016). https://doi.org/10.1038/srep35077
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep35077
This article is cited by
-
Chiral-induced switching of antiferromagnet spins in a confined nanowire
Communications Physics (2019)
-
Long-distance spin transport through a graphene quantum Hall antiferromagnet
Nature Physics (2018)
-
Field-driven dynamics and time-resolved measurement of Dzyaloshinskii-Moriya torque in canted antiferromagnet YFeO3
Scientific Reports (2017)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.