Introduction

Phase transitions are ubiquitous in physics, and account for the fundamental change of the state of a system when a control parameter is driven across a critical point. Continuous phase transitions are characterized by the divergence of the correlation length and relaxation time. As a result of the critical slowing down, the dynamics induced by a finite-time quench across the critical point is generally nonadiabatic and results in the formation of topological defects. The implications of the nonadiabatic nature of the critical dynamics during symmetry breaking were discussed by Kibble1,2 in a cosmological setting. Soon after, Zurek pointed out that condensed matter systems provide a test-bed for this scenario3,4, and predicted that the density of the topological defects scales with the transition rate 1/τQ as a universal power law of the form , where β > 0 is a function of the critical exponents of the phase transition and the dimensionality of the system. The so-called Kibble-Zurek mechanism (KZM) shows that the equilibrium critical exponents can be used to predict the density of defects formed in the non-equilibrium critical dynamics and constitutes a prominent paradigm in non-equilibrium physics5.

The applicability of the KZM is expected to extend from low-temperature physics to cosmology. Experimental efforts in a variety of systems including liquid crystal6,7, superfluid helium 38 and 49, low temperature Bose-Einstein condensates10,11, trapped ions12,13,14, multiferroic hexagonal magnanites15 and colloidal systems16 have verified aspects of the mechanism, while the scaling of excitation as a function of the quench rate across the quantum critical point remains elusive17. The situation is even more uncertain in the quantum regime. Theoretical studies18,19,20,21 and moderate experimental progress22,23,24 support the tenets of the mechanism, but a direct test is still missing. Despite the development of cooling techniques in optical lattice25 and trapped ion systems26, the experimental study of the KZM across a quantum phase transition remains challenging. This is due to the fact that the system of interest should be cooled to its ground state, and that an accurate control of the parameter driving the transition over a large range of values is required. In addition, the resulting non-equilibrium state should be probed with high-efficiency. Regarding the choice of the system, the transverse field Ising model (TFIM) is the paradigmatic model to study quantum phase transitions27, and constitutes an ideal test-bed to investigate the KZM in the quantum regime. However, simulation of this spin system in optical lattice can only be realized in some special situation28. By contrast, it has been realized in trapped ion systems29,30,31,32, but with a limited system size preventing the test of the KZM.

In this work we report the quantum simulation of the critical dynamics in the TFIM with a well controlled trapped ion in momentum space. We exploit the mapping of the TFIM critical dynamics to a set of independent Landau-Zener (LZ) crossings in pseudo-momentum space19. Firstly, we study an essential ingredient of the KZM in our setup, the so-called adiabatic-impulse (AI) approximation, that successfully accounts for the dynamics of a single LZ crossing33,34. By comparison to previous experiments35, trapped ion qubit exhibits long coherence times36. After exploiting this fact, we study the universal scaling of excitation as a function of the quench rate across the quantum critical point of the TFIM. Our experimental results show that the measured density of the excitations is in accordance with the theoretical prediction of the KZM in the quantum regime.

Results

Theory

In one dimension, the Hamiltonian of the TFIM with linear quench is defined by

where N is the number of spins, g(t) is the amplitude of the magnetic field, ΔI is the quenching rate, σx and σz are Pauli matrices, and J sets the energy scale of the system. In what follows we consider periodic boundary condition such that and denote by |→〉 the eigenvector of σx with eigenvalue 1 and by |↑〉 and |↓〉 the eigenvectors of σz with eigenvalues 1 and −1, respectively. As the parameter g(t) is changed from +∞ to 0, the Ising chain exhibits a quantum phase transition in which the ground state changes from a paramagnetic state, |→ → ··· →〉 to a doubly degenerate ferromagnetic ground state, with all spins pointing up |↑↑ ···↑〉 or down |↓↓ ···↓〉. The critical point is located at gc = 1. When varying g(t) across this value, adiabatic driving is not possible due to the closing of the gap between the ground state and the first excited state as g(t) → gc. As a result, the dynamics of the phase transition is intrinsically nonadiabatic and formation of kinks at the interface between different domains is expected. These excitations, quantum in nature, can be pictured as coherent superpositions of the form |↓↓ ···↓↑↑ ···↑↓↓ ···↓〉. Consider the preparation of the system in the paramagnetic ground state of the Hamiltonian with g(t) ≫ gc = 1, followed by crossing of the phase transition by ramping down the magnetic field g(t) to a final zero value. The time-dependence of g(t) can be linearized in the proximity of the critical point as g(t) = −t/τQ, where τQ sets the quench time scale in which the transition is crossed and the time of evolution varies from t/τQ ≪ −1 to 0. According to KZM, the density of the kinks after the transition scales as a universal power-law with the quench rate

Generally, the exact form of the density of the topological defects in a many-body system is difficult to determined. However, as pointed out by Dziarmaga19, the density of kinks in the TFIM can be exactly computed. Using the Jordan-Wigner and Bogoliubov transformations, the TFIM can be mapped to a set of independent quasi-particles. The resulting density of kinks at the end of the quench t = 0, can be measured via the expectation value of the operator

where γk is the annihilation operator of the quasi-particle with pseudo-momentum k at t = 0 and the pseudo-momentum k take N different values , where a is the lattice spacing. The operator γk is related to the initial Pauli matrices by the Bogoliubov-de Gennes and Jordan-Wigner transformation19. Therefore, different modes decouple in Fourier space and the density of the kinks at t = 0 can be calculated as the sum /N, where Ψ(0) is the finally state of the quench at t = 0. The dynamics of independent quasiparticles is described by the time-dependent Bogoliubov-de Gennes equation, whose solution determines the excitation probability in each mode, 19. The dynamics in each mode can be cast in the form of a Landau-Zener (LZ) problem,

where μk and νk are time-dependent Bogoliubov parameters for pseudo-momentum k, τk = 4τQsin(ka)(t/τQ + cos(ka)), and τQ = 1/ΔI. Comparing with the standard LZ model , the parameters τk and Δk play the role of t and Δ, respectively. As a result, each probability pk can be found by carefully controlling the parameters Δk, varying τ from −∞ to τk,f = 2τQsin(2ka) (corresponding to g(t) = 0), and measuring the probability of the excited state in the final state. Using the LZ formula for pk37, the density of the kinks can be calculated as19:

This agrees with the universal power-law scaling predicted by the KZM (2), and further shows that the prefactor is overestimated by KZM.

To experimentally study the density of the kinks in the TFIM resulting from a sweep through the critical point, an accurate control of the LZ model is necessary over a large range of values of the control parameter. In ref. 38, a special situation of the LZ supporting the AI approximation has been demonstrated in linear optics. However, that setup could not be used to implement a LZ crossing for the long evolution times required to study critical dynamics. By contrast, a trapped ion allows for a long coherence time and a high fidelity initializing, manipulating, and detecting the ion quantum state39, making it an ideal platform to complete the full evolution in the LZ model and investigate the KZM in the TFIM.

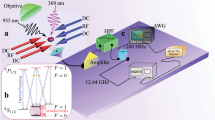
The LZ model is realized with a single 171Yb+ ion confined in a Paul trap, consisting of six needles placed on the x-z and y-z planes, as shown in Fig. 1A. The hyperfine clock transition in the ground state S1/2 manifold is chosen to realize the qubit, with energy levels denoted by and 36. In zero static magnetic field, the splitting between and is 12.642812 GHz. We applied a static magnetic field of 4.66 G to define the quantization axis, which changes the to resonance frequency to 12.642819 GHz and creates a 6.5 MHz Zeeman splittings for 2S1/2, F = 1. In order to manipulate the hyperfine qubit with high control, the coherent driving is implemented by a microwave with IQ modulation, see the scheme in Fig. 1C. A two channel Arbitrary Function Generator (AFG) creates signals around 2 MHz to modulate 3.0 GHz microwave from SG384, a 9.64 GHz microwave is mixed with the modulated 3.0 GHz signal to get an arbitrary microwave near 12.642 GHz, and then the signal is amplified to 2 W and irradiated to the trapped ion by a horn antenna. We first use Doppler cooling and initialize the qubit into the state by optical pumping as in ref. 36, then send the microwave sequence to the ion, and finally measure the population of the bright state by fluorescence detection scheme36. (The performance of the qubit is shown in supplementary).

Figure 1
figure 1

Experimental setup using an ion-trap.

(A) Configuration of six needles of the trap used in experiment. (B) 171Yb+ energy spectrum: the hyperfine energy levels (|0⟩ and |1⟩) of the ground state are used as the qubit. (C) Microwave control scheme of the driving field around 12.642 GHz: the frequency is generated by mixing microwaves between 9.64 GHz and 3 GHz, while 3 GHz microwave is IQ modulated by a dual channel AFG around 2 MHz.

Full size image

LZ dynamics and the AI approximation

For the quantum simulation of the KZM, we first characterize the LZ dynamics. According to Damski33 a LZ crossing can be well described by the adiabatic-impulse (AI) approximation which plays the central role in the KZM.

Consider the time-dependent Hamiltonian , where v is the energy detuning rate and Ω0 is the Rabi frequency of the system when detuning vt = 0. The AI approximation splits the time evolution during a LZ crossing into three sequential stages during which the dynamics is adiabatic, effectively frozen, and adiabatic again. The three regions can be separated by the freeze-out time scale , at which the equilibrium relaxation time τ = ħ/gap(t) set by the inverse of the instantaneous gap matches the time measured from the avoided crossing, e.g. . The impulse region extends over the interval (, ), when the system can not follow the external quench and is effectively frozen. Considering the difference between the LZ and second order phase transition near t = 0 (the gap closes at the critical point), the energy gap finite as (where τ0 = 1/Ω0 and τQ = 1/Δ), the equation determining the freeze-out time should be modified in a LZ crossing with a linear parameter α as34: .

Using the AI approximation, the probability of the excited state in LZ can be predicted as the overlap between the instantaneous ground state at and the excited state at 33. For the generic scheme A, the initial state is prepared at the ground state of the system which is far away from the critical point. The probability of the excited state at the end time tf → ∞ is then given by , where , xα = ατQ/τ0.

Experimentally, after Doppler cooling and initializing the ion state into , a microwave sequence is applied to the ion. For case A, the microwave is a phase continuous frequency sweep waveform near the spin transition. The time dependence of a typical LZ transition probability to is shown in Fig. 2B, where t = 0 is set by the microwave frequency resonating with the clock transition. Ω0 = 18.3 KHz, v = 2.0 GHz/s, and the time evolution starts from ti = −500μs. We measured the probability in the excited state for different values of the quench time τQ, by changing the frequency sweeping rate. Data and fitting results are plotted in Fig. 2C. The fitted scaling parameter α = 1.58 ± 0.01 is in agreement with the theoretical value π/234.

Figure 2
figure 2

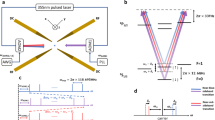
LZ transition and density of detects for different cases.

(A,D) schematic energy level and initial condition of two evolution case, respectively. (B) A typical plot of measured probability of state of 171Yb+ during the LZ crossing with evolution time starting from t = −500 μs for (A), experimental parameter: Ω0 = 18.3 KHz, v = 2.0 GHz/s; (E) a typical plot of measured probability of with starting time at t = 0 with experimental parameters: Ω0 = 13.8 KHz, v = 5.0 GHz/s, black dots: data, blue lines: numerical simulation. (C,F) Density of defects for (A,D), respectively, black dot: measured data, red dot line: the fitting line, blue dash line: theory curve in ref. 34.

Full size image

In the scheme B, the initial state is prepared in the ground state of the system at anticrossing center, ti = 0. As tf → ∞, . A typical transition probability as a function of time is shown in Fig. 2F. In order to prepare the initial state in the ground eigenstate, which is , we implement a qubit rotation microwave pulse before the microwave frequency sweep. The fitted scaling parameter to the measurement data for different quench times, α = 0.78 ± 0.03, is in accordance with the theoretical prediction π/434.

Quantum simulation of the KZM in TFIM

We have shown that a trapped ion can be used to simulate the LZ process with high accuracy. The exquisite control of this system renders the study of the KZM in TFIM feasible. To this end, we implement the following experimental scheme with a trapped ion:

  1. 1

    The Rabi frequency of the system Ω0, that corresponds to the energy scale J = ħΩ0 in the simulated Ising model, is measured and kept stable during the whole experiment. For a given quench time τQ, the experimental values of τk,f and Δk required to control the microwave at different k-modes are found via the equations τk,f = 2τQsin(2ka) and .

  2. 2

    Waveforms of first momentum parameter (k1) are computer-generated and set to AFG channels; the experiment is run repeatedly to estimate the mean density of excitations, according to the experiment control process shown in Fig. 3A. Photon counts from the bright state are recorded after is prepared in the reference pulse, which is used to normalize photon counts of the excitation pulse, to get the excitation probability.

    Figure 3
    figure 3

    Quantum simulation of the critical dynamics in the TFIM with a series of uncoupled LZ crossings.

    (A) Control process for measurement as a function of time; (B) Excitation probabilities in each of the k modes, black dots, red squares and blue triangles are data measured with JτQ/ħ at 1.85, 0.85 and 0.35, respectively. Corresponding lines are numerical calculation; (C) Density of kinks (nex) for different quench time, the fitted scaling parameter is .

    Full size image
  3. 3

    This procedure is repeated to get the excitation probability in each mode, pk.

The k-mode control sequence consists of a wave with sweeping rate of vk = ΔkΩ0 and an operation pulse RX(π)RY(θk). The Rabi frequency of the system is typically 20 KHz; we start to sweep microwave with 2 MHz detuning, so that the initial condition is located far away from anticrossing point. The RX(π)RY(θk) operation pulse transforms the excited state of the Hamiltonian at τk,f to the ion bright state , with a rotation angle θk = Δk ⋅ τk,f.

Implementing this scheme, the excitation probability in the broken-symmetry phase of a quantum Ising chain of 50 spins is measured, see Fig. 3B. Black, red and blue dots denote data measured with relative quench time at 1.85, 0.85 and 0.35, respectively. The solid lines correspond to the numerical simulations. Applying equation P = ∑ pk/N, kink densities for different quench times can be obtained. Figure 3C depicts the variation of the kink density with ħ(JτQ)−1. The scaling behavior becomes apparent in a double logarithmic plot, and a fit to the data leads to that accords with the power-law predicted by the KZM across the quantum phase transition.

Discussion

We have demonstrated that a well-controlled trapped ion offers a quantum platform to study the KZM in TFIM in pseudo-momentum space by exploiting the mapping of the critical dynamics to a set of independent LZ processes. Our experiment test the validity of the AI approximation in the LZ and the quantum KZM in the TFIM. The power-law exponent measured in our experiment is 0.59 ± 0.03 matches the numerical simulation in ref. 18 which reported the value 0.58 for the quantum Ising chain. In addition, the prefactor of the density of excitations in our experimental results is 0.136 ± 0.004 which agrees with the 0.16 estimated from numerical simulations in ref. 18. As a result, our experimental quantum simulation reveals the signature of universality in the quantum critical dynamics, the main prediction of the KZM. We notice that our scheme can be readily applied to test a variety of protocols, including the critical dynamics under inhomogeneous driving40, nonlinear quenches41,42, and the simulation of multiple-body interactions required for counterdiabatic driving and the suppression of the KZM across a quantum phase transition43,44,45. As a result, it constitutes an ideal experimental platform for the quantum simulation of nonequilibrium many-body systems in momentum space. The limitations of our setup is that it can only simulate the KZM dynamics in momentum space and cannot probe topological defect formation in real space.

Methods

Ion trap setup

The size of the needle trap depends mainly on the distance between the two needles tips near the trap center, which is set to 120 μm in the experiment. The needle trap is installed in an ultrahigh vacuum below 10−11 torr, and a helical resonator provides the RF signal with frequency of 27 MHz and amplitude of 150 V to the trap, that sets the ion secular motion frequencies to 1.45 MHz, 1.66 MHz and 2.96 MHz. Ion fluorescence is collected by an objective lens with 0.4 numerical aperture (N.A), and detected by a photomultiplier tube (PMT). Total fluorescence detection efficiency is ηtotal = ηlens ⋅ ηtrans ⋅ ηdetect = 4% × 90% × 30% = 1.1%

Waveform of the driving microwave

In principle, any required waveform of the microwave field can be generated by setting the waveforms of dual channel AFG for IQ modulation. We consider the carrier microwave Bc(t) = Asin(ωct), with amplitude A and frequency fc = ωc/2π. The waveforms generated by AFG for IQ modulation are I(t) = cos(ϕ(t)) and Q(t) = sin(ϕ(t)) respectively. After IQ modulation, the microwave field will be B(t) = Asin(ωct + ϕ(t)), where the phase function ϕ(t) can be expressed in a section function for the microwave composed of a series of frequency sweeping waveforms and qubit rotation pulses. With a qubit resonance frequency f0 = ω0/2π, we sweep the microwave frequency at ω1 from t = 0, with sweeping rate v to t = t1. Then the qubit is manipulated with Ry in (t1, t2) and Rx in (t2, t3). The expression of ϕ(t) can be derived

where , ϕ2 = ϕ1 + (ω0 − ωc)(t2 − t1).

In actual experiment, there is a residual carrier wave with small amplitude εc, resulting from the imperfection of the IQ modulation . While the ratio of amplitudes εc and A is small, εc/A < 0.01, when the scheme works in resonance modulation ω0 = ωc the residual carrier wave can change the qubit state inducing an error over one percent after several Rabi flips. In order to reduce this error, we set ωc such that ω0 − ωc = (2π)2.0 MHz, which is largely detuned from resonance compared to the Rabi frequency Ω0 = (2π)20 KHz, and renders the residual wave drive negligible.

Additional Information

How to cite this article: Cui, J.-M. et al. Experimental Trapped-ion Quantum Simulation of the Kibble-Zurek dynamics in momentum space. Sci. Rep. 6, 33381; doi: 10.1038/srep33381 (2016).