Abstract
Defects in semiconductors can exhibit multiple charge states, which can be used for charge storage applications. Here we consider such charge storage in a series of oxygen deficient phases of TiO2, known as Magnéli phases. These Magnéli phases (TinO2n−1) present well-defined crystalline structures, i.e., their deviation from stoichiometry is accommodated by changes in space group as opposed to point defects. We show that these phases exhibit intermediate bands with an electronic quadruple donor transitions akin to interstitial Ti defect levels in rutile TiO2. Thus, the Magnéli phases behave as if they contained a very large pseudo-defect density: ½ per formula unit TinO2n−1. Depending on the Fermi Energy the whole material will become charged. These crystals are natural charge storage materials with a storage capacity that rivals the best known supercapacitors.
Similar content being viewed by others
Introduction
As our energy requirements grow and alternative energy sources become an integral part of most countries’ energy matrices, energy carriers, in particular charge storage systems play an ever increasing role. Li-ion batteries have played the major role in energy storage up to now1, but new systems termed supercapacitors2 have emerged and are becoming more popular. In this case, a number of materials - mainly metal oxide thin films - provide charge storage due to the presence of defects inside its porous structure3,4,5,6. We present an alternative strategy to design charge storage materials, based on Magneli phases of titanium oxide TinO2n−17. These can be considered as oxygen-deficient phases of TiO2, but the off-stoichiometry is accommodated by changes in the crystal structure, manifested as shear planes, as opposed to point defects, such as oxygen vacancies or Ti interstitials.
Titanium oxides are important materials for applications in photocatalysis8,9,10, energy storage11,12 and memory devices13,14,15. The stoichiometric phases of this material, rutile, anatase and brookite TiO2 are known to present unintentional n-type doping at ambient conditions, owing in part to intrinsic point defects related to oxygen deficiency: oxygen vacancy (VO) and titanium interstitial (Tii)16,17,18. Further increase in oxygen deficiency leads to the formation of the shear planes and consequently a phase transition to the Magnéli phases19. These phases of TinO2n−1 also find wide spread applications20 such as catalysts, as an active material for the remediation of aqueous waste and contaminated water21, as fuel cells and as batteries22,23.
A few reports on the thermochemistry24,25, electrical properties26 and electronic structure27,28,29,30,31 of such systems are available, but the possibility of electronically charging them remains uncharted territory. Such charging becomes relevant as these materials are used as the active media of memristor devices19,32 or in storage applications11,12 and in those cases, the exchange of electrons with a reservoir must be taken into account.
In this manuscript we study the stability and electronic structure of Magnéli phases Ti4O7 and Ti5O9, as well as of the corundum Ti2O3 phase, while in contact with a reservoir of electrons. We show that these TiO phases present a series of properties akin to Tii-containing rutile TiO2, such as mid gap states and charge state transitions. We show that the intermediate band typical for the Magnéli phases can donate electrons to an electron reservoir, leading to a new electronic phase that resembles charged defects in a semiconductor, even though they contain no crystallographic defects. The combination of such properties is shown to enable charge storage in these systems in such an efficient way that they can rival the best supercapacitors to date2.
Results and Discussion
The Magnéli phases have the general oxygen-deficient chemical formula TinO2n−1 (n > 4). In general, for n > 37 the crystal structure is still rutile TiO2, containing point defects or Wadsley defects. Further removal of oxygen (a decrease in n) leads to the reorganization of the crystal into these new crystallographic phases19,33. These phases can be described as being composed of rutile-like chains (edge- and corner-sharing arrangement) of n TiO6 octahedra units along the c axis bounded by a corundum structure (i.e. Ti2O3, composed of face-sharing TiO6 octahedra)34,35,36. From this point of view, these phases can be interpreted as an ordered combination of rutile TiO2 and corundum Ti2O3 parts. The corundum-like boundaries of the rutile-like region of the Magnéli phases are usually referred to as shear planes. A detailed view of the corundum structure is shown in Fig. 1, where we observe the existence of edge-sharing octahedra.
(a) Rutile TiO2, (b,c) corundum Ti2O3 view along and parallel to the c axis respectively and (d) Magnéli phase Ti4O7 structures. Ti atoms are blue spheres enclosed by blue octahedra while oxygen atoms are red spheres on the edges of the octahedra. In (d) the blue lines enclosure the four-units rutile-like chains along the c direction, bounded by corundum-like planes restricted to the (001) planes.
A model structure of these oxygen deficient phases can be obtained from rutile via a shear operation  25,31,37,38. This operation can be understood as successive displacements of the atoms in the rutile crystal. All atoms above each (121) plane shifted n times along the c vector from the origin are in turn dislocated in the
25,31,37,38. This operation can be understood as successive displacements of the atoms in the rutile crystal. All atoms above each (121) plane shifted n times along the c vector from the origin are in turn dislocated in the  direction of the rutile structure. This direction coincides with a lattice vector of the oxygen subnet–i.e., the vector
direction of the rutile structure. This direction coincides with a lattice vector of the oxygen subnet–i.e., the vector  connects two oxygen atoms in the rutile crystal–, thus it maps the dislocated atoms of that species into atoms of the same species and finally leaves the lattice positions for oxygen atoms unchanged. Figure 1 shows the structures of rutile TiO2 and Ti4O7. From the perspective of (a) and (b) one can see that the oxygen deficiency of such compounds is better described by extra Ti atoms occupying interstitial positions of the TiO2 matrix, rather than by oxygen atoms missing at specific lattice sites, i.e., oxygen vacancies.
connects two oxygen atoms in the rutile crystal–, thus it maps the dislocated atoms of that species into atoms of the same species and finally leaves the lattice positions for oxygen atoms unchanged. Figure 1 shows the structures of rutile TiO2 and Ti4O7. From the perspective of (a) and (b) one can see that the oxygen deficiency of such compounds is better described by extra Ti atoms occupying interstitial positions of the TiO2 matrix, rather than by oxygen atoms missing at specific lattice sites, i.e., oxygen vacancies.
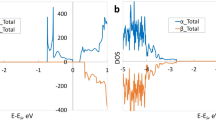
From the electronic point of view, these oxygen-deficient TinO2n−1 phases present an intermediate band27,28,30 slightly below the conduction band minimum (CBM). This is shown by the projected density of states (PDOS) given for Ti2O3 and Ti4O7 in Fig. 2 and for Ti5O9 in Fig. 3 (upper panel). These DOS show striking resemblance to those observed for isolated defects in TiO216,17,18 and thus, we describe these states to be due to the presence of pseudo-defects inside the Mangéli phases. As these phases present a high concentration of such pseudo-defects, one can think of this intermediate band as the spatially-extended generalization of point defects. Importantly, this pseudo-defect band lies close to the rutile TiO2 CBM, indicating that its occupation can be tuned by the use of appropriate leads, leading to charging of the material. We investigate this charging process by electronic structure calculations of the first two Magnéli phases Ti4O7 and Ti5O9 and corundum-phase Ti2O3.
Projected density of states for (a) Ti2O3 and (b) Ti4O7. The spin components are distinguished by the upper and lower panels on each graph. The black full line is the total DOS and the red dashed line represents Ti(d) contribution. Energies are referenced from the last occupied level of the host material (TiO2) by core-level (Ti 1s) shifts. The full vertical red line indicates the most energetic occupied level of each compound, while the vertical dashed blue line indicates the TiO2 CMB.
Projected Density of States (PDOS) for all charge states of Ti5O9.
The full black line is the total DOS and the red dashed line represents Ti(d) contribution to the DOS. The two spin components are represented by positive and negative values along vertical axis. The vertical full red line indicates the last occupied electronic level. Energies are referenced from the last occupied level of the host material (rutile TiO2).
The depletion of oxygen from TiO2 and the ensuing formation of these oxygen-deficient phases can be described by two processes: (i) either the Magnéli phase is formed by the removal of oxygen and consequently the formation of ordered VO planes (secant to the c vector, see Fig. 1) or (ii) from the formation of Tii in ordered planes, i.e.,


Our calculations include a reservoir of atoms at constant chemical potential μα (α = Ti, O) and a reservoir of electrons with the chemical potential at EF. The formation enthalpy  with respect to TiO2 as a host material is given by
with respect to TiO2 as a host material is given by

where EH and ED(q) are respectively the total energies of the system before (TiO2) and after (TinO2n−1) exchanging mα atoms with the reservoirs. The total energies ED and EH are obtained from density-functional calculations performed using the VASP code39 using the hybrid functional proposed by Heyd, Scuseria and Ernzerhof (HSE)40. This methodology include many-body effects that can successfully describe the different valence states of the Mangnéli phases, as reported in the paper of Stoyanov et al.41. The plane wave cutoff is set at 520 eV for all calculations and k-point sampling through the Brillouin zone was performed via the Monkhorst-Pack scheme. For charged systems, the unit cell volume is fixed as that of the uncharged system and atomic positions within the unit cells are relaxed. Our choice is justified by recent experimental results showing the formation of oxygen-deficient crystalline phases inside a TiO2 matrix15. Test calculations where the unit cell was allowed to fully relax were performed, resulting in the same qualitative behavior (see supplementary material for further details). The Fermi energy EF is given with respect to the VBM of TiO2 (EV BM) and ΔV is a band-bottom alignment correction used to place all energies at the same reference, obtained from core level shifts42. For Ti atoms the 3p4s3d electrons were considered as valence electrons whereas the 2s2p configuration was considered for O atoms. Core level energies were obtained solving the Kohn-Sham equations for these inner level electrons subjected to a potential given by the pseudopotential method projector-augmented-wave (PAW) scheme43. In our calculations the chemical potential of oxygen was obtained from the O2 molecule while the same quantity for the titanium atom was obtained from a bulk calculation of the hcp structure of metallic Ti.
Typically one uses equation 3 to address the formation enthalpy of defects. Here however we use this methodology to calculate the stability of the pseudo-defects in Magnéli phases for different charge states q. The chemical potentials one should use for the expression could be either μO for the removed oxygen (Eq. 1; mO > 0) or μTi for the added titanium (Eq. 2; mTi < 0). We choose to discuss only the situation where the Magnéli and corundum phases are formed via the insertion of Ti atoms (Eq. 2) because the electronic properties of the TinO2n−1 phases studied here exhibit pseudo-defect properties as if the material were rutile TiO2 doped by Ti interstitial. Moreover, the formation enthalpies for the reaction in Eq. 1 can be obtained by using the oxygen chemical potential μO, being the difference in the enthalpy curves in that case just constant shifts to the values presented here; the charge transfer properties remain identical.
Formation enthalpies for the Ti2O3, Ti4O7 and Ti5O9 structures (when one considers α = Ti and mα = +1 in equation 3), as well as the same data for the Tii in rutile TiO2 obtained from Lee et al.16 are depicted in Fig. 4. O-rich and Ti-rich conditions are obtained by using the boundaries for μTi given by the stability condition of each compound. Notice that Ti2O3 presents the full ionized charge state (+4) as the most stable (lowest formation energy) spanning the entire rutile TiO2 band gap, while both Ti4O7 and Ti5O9 present the same trend from the VBM up to ε(+4/0) = ECBM − 0.36 eV and 0.48 eV respectively. The position of ε(+4/0) marks an abrupt transition from the +4 state to the neutral state. Interestingly this transition lies close to the very same ε(+4/0) for the isolated Tii in rutile TiO2 (0.29 eV)16. Thus our defect-free TinO2n−1 structures behave in a fashion similar to TiO2 with intrinsic defects (Tii or VO). An important distinction must be taken at this point, since the presence of extrinsic defects can lead to different behaviors. For example, nitrogen impurities in the Magnéli phases lead to an electron-hole compensation effect that can significantly alter properties such as the bandgap and photocatalytic activity44. We emphasize the fact that we vary the occupation of the pseudo-defect induced intermediate band in a similar fashion as it is done to mid gap states of isolated defects inside semiconductors. Moreover both Ti4O7 and Ti5O9 present negative-U behavior45. This is also the case of Tii point defects inside rutile TiO216.
Formation enthalpies for (a) Ti2O3, (b) Ti4O7, (c) Ti5O9, (d) and Tii point defect in rutile TiO2. The Tii formation energies shown on (d) are from ref. 16. The thick black lines emphasize the lowest energy charge state for each occupation for the entire band gap span and the transitions from +4 charge state to the neutral charge state in Ti4O7, Ti5O9 and TiO2 are also featured as ε(4+/0).
The nature of the charged state in the TinO2n−1 structures can be understood from the Projected Density of States (PDOS) and real-space projections of selected states. Figures 3 and 5 show this kind of analysis for Ti5O9 as a point in case—Ti4O7 presented a similar behavior (see supplementary material). The neutral structure shows a midgap intermediate band akin to isolated defect states. These states are mostly of Ti(d) character—as are the unoccupied bands—delocalized over several Ti atoms, as shown in Fig. 5. It is known from literature that 3d transition metal related defects exhibit multiple charged states46,47 as is the case of Tii in rutile TiO216. Recently, such charge transitions have also been observed for extended defects47. Here, we show that even perfect crystals that deviate from stoichiometry may exhibit similar charge states. The d orbital rehybridization seen in Fig. 5 suggest that these multiple charge states of the pseudo-defects in the Magnéli phases are facilitated by a self-regulating response mechanism46,48,49 which also explains why the material does not undergo a Coulomb catastrophe.
Real space projection of the intermediate band on the PDOS of Fig. 3, from EF − 1.5 eV to EF from all charged states with the exception of +4.
The isosurfaces are depicted for all charge states, from the neutral case to +4 from left to right. We plot the same isosurface (10−2 e · Bohr−3). The +4 charge state presents no intermediate band, the structure is presented only for the sake of completion.
To estimate the storage capacity of these Magnéli phases, we consider a maximum of 4 holes per pseudo-defect corresponding to the quadruple donor transition observed, as well as the maximum capacity of the intermediate band to accommodate 4 electrons—two electrons for each of the two VO’s, or alternatively, four electrons for a single Tii, according to the previous discussion. Using this and considering a device operating at a 1 V potential, the theoretical maximum capacitance is approximately 1300 F/g for Ti2O3, 600 F/g for Ti4O7 and 500 F/g for Ti5O9, placing those systems at par with materials used to build supercapacitors. One of the best supercapacitors developed until now is based on nickel hydroxide nanoflakes on carbon nanotube composite electrode, with a capacitance of 3300 F/g50. As discussed earlier, by interfacing these oxygen deficient phases appropriate leads, one can control its charge state.
Conclusions
In conclusion, we have performed electronic structure DFT calculations to asses the formation and electric charging of the TiO Magnéli and corundum phases. We show that these materials contain pseudo-defects, i.e., they behave akin to Tii doped rutile TiO2 with a concentration of ½ quadruple donor defects per formula unit TinO2n−1. These pseudo-defects are characterized by an intermediate band that can be charged, thus, the material can become charged and used for high-capacity charge storage. We propose that the same behavior shown here for the oxygen deficient TiO phases exists in other semiconductor materials. The required condition is the presence of the intermediate band with a large enough density of states, which we expect to be the case in other materials that present stable phases over a wide range of stoichiometries.
Additional Information
How to cite this article: Padilha, A. C. M. et al. Charge storage in oxygen deficient phases of TiO2: defect Physics without defects. Sci. Rep. 6, 28871; doi: 10.1038/srep28871 (2016).
References
Goodenough, J. B. & Park, K.-S. The Li-ion rechargeable battery: A perspective. J. Am. Chem. Soc. 135, 1167–1176 (2013).
Yu, Z., Tetard, L., Zhai, L. & Thomas, J. Supercapacitor electrode materials: Nanostructures from 0 to 3 dimensions. Energy Environ. Sci. 8, 702–730 (2015).
Sugimoto, W., Iwata, H., Yasunaga, Y., Murakami, Y. & Takasu, Y. Preparation of ruthenic acid nanosheets and utilization of its interlayer surface for electrochemical energy storage. Ang. Chem. Int. Ed. 42, 4092–4096 (2003).
Toupin, M., Brousse, T., Blanger, D. & Be, D. Charge storage mechanism of MnO2 electrode used in aqueous electrochemical capacitor. Chem. Mat. 3184–3190 (2004).
Simon, P. & Gogotsi, Y. Materials for electrochemical capacitors. Nature Mat. 7, 845–854 (2008).
Young, M. J., Holder, A. M., George, S. M. & Musgrave, C. B. Charge storage in cation incorporated α-MnO2 . Chem. Mat. 1172–1180 (2015).
Andersson, S., Collem, B., Kuylenstierna, U. & Magnéli, A. Phase Analysis Studies on the Titanium-Oxygen System. Acta Chem. Scan. 1641 (1957).
Linsebigler, A. L., Lu, G. & Yates, J. T. Photocatalysis on TiO2 surfaces: Principles, mechanisms and selected results. Chem. Rev. 95, 735–758 (1995).
Di Valentin, C., Pacchioni, G. & Selloni, A. Electronic structure of defect states in hydroxylated and reduced rutile TiO2(110) surfaces. Phys. Rev. Lett. 97, 166803 (2006).
Krüger, P. et al. Intrinsic nature of the excess electron distribution at the TiO2(110) surface. Phys. Rev. Lett. 108, 126803 (2012).
Zhang, Y. et al. An electrochemical investigation of rutile TiO2 microspheres anchored by nanoneedle clusters for sodium storage. Phys. Chem. Chem. Phys. 17, 15764–15770 (2015).
Oh, S. M. et al. High electrochemical performances of microsphere c-TiO2 anode for sodium-ion battery. ACS Appl. Mat. Int. 6, 11295–11301 (2014).
Wilk, G. D., Wallace, R. M. & Anthony, J. M. High-k gate dielectrics: Current status and materials properties considerations. J. Appl. Phys. 89, 5243–5275 (2001).
Strukov, D. B., Snider, G. S., Stewart, D. R. & Williams, R. S. The missing memristor found. Nature 453, 80–83 (2008).
Kwon, D.-H. et al. Atomic structure of conducting nanofilaments in TiO2 resistive switching memory. Nature Nanotech. 5, 148–153 (2010).
Lee, H.-Y., Clark, S. & Robertson, J. Calculation of point defects in rutile TiO2 by the screened-exchange hybrid functional. Phys. Rev. B 86, 075209 (2012).
Morgan, B. J. & Watson, G. W. Intrinsic n-type Defect Formation in TiO2: A Comparison of Rutile and Anatase from GGA+U Calculations. J. Phys. Chem. C 114, 2321 (2010).
Janotti, A. et al. Hybrid functional studies of the oxygen vacancy in TiO2 . Phys. Rev. B 81, 085212 (2010).
Szot, K. et al. TiO2–a prototypical memristive material. Nanotechnology 22, 254001 (2011).
Walsh, F. C. et al. The continuing development of Magnĺi phase titanium sub-oxides and Ebonex electrodes. Electrochimica Acta 55, 6342 (2010).
Chen, G. et al. Electrolytic reduction of trichloroethylene and chloroform at a Pt- or Pd-coated ceramic cathode. J. Appl. Electrochem. 33, 161 (2003).
Rashkova, V. et al. Electrocatalytic behavior of thin Co-Te-O films in oxygen evolution and reduction reactions. Electrochim. Acta 54, 3794 (2007).
Kao, W.-H. et al. Formation enhancement of a lead/acid battery positive plate by barium metaplumbate and Ebonex. J. Electrochem. Soc. 144, 1907 (1997).
Liborio, L. & Harrison, N. Thermodynamics of oxygen defective Magnéli phases in rutile: A first-principles study. Phys. Rev. B 77, 1–10 (2008).
Harada, S., Tanaka, K. & Inui, H. Thermoelectric properties and crystallographic shear structures in titanium oxides of the Magnéli phases. J. Appl. Phys. 108, 083703 (2010).
Bartholomew, R. & Frankl, D. Electrical properties of some titanium oxides. Phys. Rev. 187, 828–833 (1969).
Liborio, L., Mallia, G. & Harrison, N. Electronic structure of the Ti4O7 Magnéli phase. Phys. Rev. B 79, 245133 (2009).
Weissmann, M. & Weht, R. Electronic and magnetic properties of the different phases of Ti4O7 from density functional theory. Phys. Rev. B 84, 144419 (2011).
Leonov, I. et al. Charge order and spin-singlet pair formation in Ti4O7 . J. Phys. Cond. Mat. 18, 10955–10964 (2006).
Padilha, A. C. M., Osorio-Guillén, J. M., Rocha, A. R. & Dalpian, G. M. TinO2n−1 Magnéli phases studied using density functional theory. Phys. Rev. B 90, 035213 (2014).
Padilha, A. C. M., Rocha, A. R. & Dalpian, G. M. DFT+U simulation of the Ti4O7-TiO2 interface. Phys. Rev. Appl. 3, 024009 (2015).
Pan, F., Gao, S., Chen, C., Song, C. & Zeng, F. Recent progress in resistive random access memories: Materials, switching mechanisms and performance. Mat. Sci. Eng. Rep. 83, 1–59 (2014).
Bursill, L. A., Hyde, B. G., Terasaki, O. & Watanabe, D. On a new family of titanium oxides and the nature of slightly-reduced rutile. Phil. Mag. 20, 347–359 (1969).
Marezio, M. & Dernier, P. The crystal structure of Ti4O7, a member of the homologous series TinO2n−1 . J. Sol. State Chem. 3, 340–348 (1971).
Marezio, M., McWhan, D., Dernier, P. & Remeika, J. Structural aspects of the metal-insulator transitions in Ti4O7 . J. Sol. State Chem. 6, 213–221 (1973).
Le Page, Y. & Marezio, M. Structural chemistry of Magnéli phases TinO2n−1(4 ≤ n ≤ 9): IV. superstructure in Ti4O7 at 140 K. J. Sol. State Chem. 53, 13–21 (1984).
Wood, G. J. & Bursill, L. A. The formation energy of crystallographic shear planes in TinO2n−1 . Proc. R. Soc. A 375, 105–125 (1981).
Andersson, S., Templeton, D. H., Rundqvist, S., Varde, E. & Westin, G. The crystal structure of Ti5O9 . Acta Chem. Scand. 14, 1161–1172 (1960).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996).
Heyd, J., Scuseria, G. E. & Ernzerhof, M. Hybrid functionals based on a screened coulomb potential. J. of Chem. Phys. 118, 8207–8215 (2003).
Stoyanov, E., Langenhorst, F. & Steinle-Neumann, G. The effect of valence state and site geometry on Ti L3,2 and O K electron energy-loss spectra of TixOy phases. American Mineralogist 92, 577 (2007).
Li, Y.-H. et al. Revised ab initio natural band offsets of all group IV, II-VI and III-V semiconductors. Appl. Phys. Lett. 94, 212109 (2009).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953–17979 (1994).
Niu, M., Tan, H., Cheng, D., Sun, Z. & Cao, D. Bandgap engineering of Magnéli phase TinO2n−1: Electron-hole self-compensation. J. Chem. Phys. 143, 054701 (2015).
Watkins, G. D. Negative-U properties for defects in solids. Adv. Sol. State Phys. 24, 163–189 (1984).
Haldane, F. & Anderson, P. Simple model of multiple charge states of transition-metal impurities in semiconductors. Phys. Rev. B 13, 2553–2559 (1976).
Raebiger, H., Nakayama, H. & Fujita, T. Control of defect binding and magnetic interaction energies in dilute magnetic semiconductors by charge state manipulation. J. Appl. Phys. 115 (2014).
Raebiger, H., Lany, S. & Zunger, A. Charge self-regulation upon changing the oxidation state of transition metals in insulators. Nature 453, 763–766 (2008).
Wolverton, C. & Zunger, A. First-principles prediction of vacancy order-disorder and intercalation battery voltages in LixCoO2 . Phys. Rev. Lett. 81, 606–609 (1998).
Tang, Z., Tang, C.-H. & Gong, H. A High Energy Density Asymmetric Supercapacitor from Nano-architectured Ni(OH)2/Carbon Nanotube Electrodes. Adv. Funct. Mater. 22 (2012).
Acknowledgements
This work was supported by brazilian funding agencies FAPESP (grants 2011/21719-8, 2015/05830-7, 2010/16202-3, 2011/19924-2, 2016/11429-6 and 2013/22577-8) and CNPq. The support given by Cenapad-SP in the form of computational infrastructure is also acknowledged.
Author information
Authors and Affiliations
Contributions
A.C.M.P. wrote the first version of the manuscript and performed all calculations presented. All authors participated in the analysis and discussion of the results and revised the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Padilha, A., Raebiger, H., Rocha, A. et al. Charge storage in oxygen deficient phases of TiO2: defect Physics without defects. Sci Rep 6, 28871 (2016). https://doi.org/10.1038/srep28871
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep28871
This article is cited by
-
Maintaining the localized surface plasmon resonance of copper nanoparticles by defective TiO2 thin films
Applied Physics A (2021)
-
Structural, magnetic, and optical properties of degenerated Ni and (Ga/Zn) co-doped TiO2 nanocomposites
Applied Physics A (2020)
-
The crucial role of hydrogenation in the creation of ferromagnetic properties in W-doped TiO2 nano-composite
Journal of the Australian Ceramic Society (2020)
-
Photocatalytic water splitting by N-TiO2 on MgO (111) with exceptional quantum efficiencies at elevated temperatures
Nature Communications (2019)
-
The formation mechanism of tear strips on stretched Ti-22Al-25Nb alloy sheets
Scientific Reports (2017)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.