Introduction

Silicene as a counterpart of graphene has recently gained explosive studies due to its many amazing unique properties such as ultra-high carrier mobility, anomalous quantum Hall effect, and topological insulating state1,2,3. Unlike the ideal flat graphene, the silicene consists of two separate sublattices forming the low-bulked geometrical structure owe to the mixing of sp2 and sp3 hybridizations, which provide possibilities in tailoring properties by surface functionalization etc. An advantage of silicene over graphene is that it would be easily integrated into the high-performance nanoelectronics based on the current Si-based semiconductor industrial techniques. The silicene has been successfully fabricated on many supporting surfaces, such as the Ag(111)4,5, ZrB2(0001)6, Au(110)7, and Ir(111) surfaces8. Recent studies show also the possibilities in fabricating quasi free standing silicene on non-metallic substrates9,10,11,12. These progresses have paved the way for studying its peculiar properties and potential applications. Besides the studies on the synthesis of silicene, the structural defect in silicene has also attracted much attention in view of the property modulation13,14,15,16,17,18,19,20,21,22. Several theoretical studies have been devoted on investigating the geometrical structures and modification on silicene’s properties of single and double vacancy defects. For example, the self-healing of vacancy defects in silicene has been found to be driven by the energy gain through new Si-Si bond formation13. Guo et al.14 studied in detail the structure, mobility, electronic and magnetic properties of vacancy defect in silicene. Şahin et al.15 have evaluated the formation, stability, and reactivity of defect. In Berdiyorov et al.’s studies16, the effects of vacancy defect on the thermal stability of silicene has been investigated with molecular dynamics method. Interestingly, a recent experimental study17 has shown the presence of a large number of defect clusters which has recently been carefully investigated by Li et al.18 with ab initio molecular dynamics simulations.

Considering the experimental advances in patterning two-dimensional materials by regularly arranging vacancy antidots to fabricate nanomeshes23, the effects of vacancy hole on bandgap opening in silicene has been analyzed in detail19,20,21,22. A bandgap engineering mechanism–degenerate perturbation which is different to the sublattice equivalence breaking has been proposed. In fact, this phenomena could be seen in a recent experimental study on the fabricating of silicene on ZrB2(0001) surface6, where the periodic pattern of interaction between silicene and substrate modulates the boundary conditions of silicene. The silicene was actually patterned into superlattice with the Dirac cone being folded to Γ point and a bandgap was confirmed to be opened at Γ. The bandgap opening is a critical and attractive research issue for silicene to be used in photoelectronics, where a proper on/off ratio is required. The ideal free-standing silicene, though it has high velocity massless Fermions as charge carrier owe to the nearly linear energy dispersion relation around Dirac cone, has to be transferred from semimetal to semiconductor to be used for transistors in nanoelectronics. A kind of nanomeshes with Dirac cone being folded to Γ to form four-fold degeneracy could be opened a bandgap by the degenerate perturbation through introducing an inversion symmetry preserved antidot in the repeated unit. Such antidot would however not change the semimetal nature of the other nanomeshes which are still less of investigations. Actually, the π-like band splitting also happens in such nanomeshes, which is however missed in the previous studies19,20,21,22. In this paper, we would show that such band splitting can also transfer the nanomesh to be semiconducting at the aid of strain.

Results

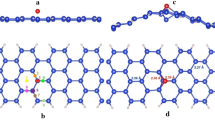
Both the hexagonal and orthogonal silicene nanomeshes could be fabricated in experiment. In this paper, we would like to concentrate on studying the orthogonal nanomeshes to facilitate the discussion of the uniaxial strains respectively applied along armchair and zigzag directions, whose conclusions could shed light on the hexagonal nanomeshes accordingly. In Fig. 1, besides the primitive unit a × b of silicene, the smallest orthogonal unit A1 × B1 with A1 = a + b and B1 = - a + b has also been schematically illustrated. The repeated unit shown in Fig. 1b for the antidot patterned nanomesh could be written as A = M A1 and B = N B1, which could be hereafter accounted by (M,N). In order to facilitate discussion, we would like to refer the defect free silicene calculated by using the (M,N) supercell as pseudo silicene superlattice (PSS). Therefore, the (1,1) PSS stands for the pristine silicene calculated with the smallest rectangle unit A1 × B1, whose bandstructure has been shown in Fig. 1c. The Dirac point is found between Γ1 and Y1. The lower panel of Fig. 1c shows the rectangular Brillouin zone (r-BZ) of (1,1) PSS and the hexagonal Brillouin zone (h-BZ) corresponding to the primitive unit cell. One could see that the K (K′) in the h-BZ is now equivalent to the () in the r-BZ, agreeing with the Dirac point position in the calculated bandstructure. Similar analysis on the (1,2) PSS shows the band folding of K (K′) point Dirac cone in h-BZ of primitive cell to the () point in r-BZ of (1,2) PSS. The corresponding bandstructure and band folding analysis are presented in Fig. 1d. The results shown in Fig. 1e for the (1,3) PSS show that its Dirac cone is folded to Γ point. Based on the detailed band folding analysis, we would like to sort the studied orthogonal lattices into three categories depending on the band folding of Dirac cone: (1) the 3p PSS (M,N) with N = 3p, folding to the Γ in the corresponding r-BZ; (2) 3p + 1 PSS with N = 3p + 1, folding to the ; and (3) 3p + 2 PSS with N = 3p + 2, folding to the . Compared to the 3p type superlattices, the 3p + 1 and 3p + 2 type superlattices are less of studies till now.

Figure 1
figure 1

The top and side views of silicene structure (a) and the schematic geometry of the nanomesh A × B patterned by regularly arranged antidots (b). The big and small balls stand for the silicon and hydrogen atoms, respectively. In (a), besides the a × b primitive unit cell, the smallest rectangle unit A1 × B1 is also shown. In (c–e), the upper and lower panels are for the bandstructures and Brillouin zones, respectively. Besides the r-BZ (red rectangle) for each PSS, the h-BZ (black hexagon) for the primitive cell is also presented for band folding analysis.

Full size image

We would like to start our studies by showing the strain effects on the 3p + 1 and 3p + 2 type PSSes. For the orthogonal lattice (M,N), the strain could be respectively applied along the armchair ( A lattice) and zigzag ( B lattice) directions, which we would like to refer as σa and σz. In Fig. 2, the (3,4) PSS is adopt as prototype to illustrate our results on the 3p + 1 lattices. The uniaxial strain would continuously shift the Dirac cone along the path. The σa would shift it toward Y point while the σz would move it close to Γ. The effects of the strain could also be accounted by the energy interval ΔE between the πz and πa as marked in the Fig. 2. As to the marked bands, we have also calculated their band decomposed charge densities. The corresponding densities of the isolated (3,4) PSS are presented in Fig. 2, which suggest the π-like bonding characters. Also, considering the fact that the electronic configuration of silicene could be regarded as the mixture of sp2 and sp3 hybrizations, we would like hereafter to discuss them as π-like bands. The densities of the πa and πz bands are found to be respectively distributed around the bonds along armchair and zigzag directions. As shown in Fig. 2, the ΔE would be enlarged (reduced) by the σz (σa) strain. Our careful analysis shows that similar strain effects could also be found in the 3p + 2 PSSes. The difference is that the ΔE would be reduced (enlarged) by the σz (σa) strain, respectively.

Figure 2: The banstructure of the free-standing (3,4) PSS and those under σz = 5% and σa = 5% unaxial strains.
figure 2

For the free-standing (3,4) PSS, the band decomposed charge densities for the bands along ΓY path as marked by πz and πa are studied at Y point with the iso-value of 0.01 e/Å3. Both top and side views are shown.

Full size image

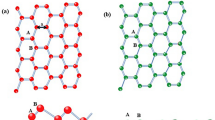
For the 3p + 1 and 3p + 2 type silicene superlattices, the defect can also induce band splitting phenomena. The inversion symmetry preserved (ISP) defect has been found to open bandgap in the 3p silicene nanomeshes, which would however not alter the conducting properties of the 3p + 1 and 3p + 2 nanomeshes19,20,21,22. The periodically arranged defects would impose new Born von Karman boundary conditions on silience to make it into superlattice24,25, which have been introduced in by the modulation of the Bravais lattice. In the defect free pristine silicene crystal, the hexagonal primitive unit cell defined by a × b (see Fig. 1) accounts for the Bravais lattice of silicene, which should correspond to the A × B periodic unit in the (M,N) superlattice. The periodically arranged defects would alter the Bravais translation symmetry to modulate the Born von Karman boundary conditions accordingly. In the ISP defect patterned superlattice, besides the previously discussed band splitting in 3p type superlattices at Γ point to open bandgap, the ISP defect in fact would also induce band splitting phenomena in the other superlattices. In order to facilitate discussion, we would like to mimic an ISP defect in silicene by contracting a silicon hexagon by about 3%, which is highlighted in Fig. 3a. In our simulations, the atoms in this hexagon have been fixed while the rest atoms are free to relax. The methodology of tight-binding method24 is believed to be efficient in dealing with silicene which could help to understand the physical origin of the electronic properties of silicene-based nanostructures. By considering only the nearest neighbor atoms, the related energy Enna could be obtained through

Figure 3
figure 3

The schematic structure of the ISP defect introduced by contracting the highlighted silicon hexagon (a) and the corresponding bandstructure (b). The π-like band splitting at Y point is marked out for eye guidance. The split bands along ΓY path are marked by πa1, πa2, πz1, and πz2 at Y point. Their band decomposed charge densities at Y point are studied in (c) with the iso-value of 0.01 e/Å3.

Full size image

where ti is the transfer integral, ki is the component of wavevector k , ai is the corresponding lattice constant, and is the atomic orbital. According to the TB method, the ~3% contraction of the Si-Si bonds in the highlighted silicon hexagon would enhance the corresponding transfer integrals to introduce perturbation to the electronic properties of silicene. Such periodically arranged perturbation would then make the silicene superlattice. In Fig. 3, in such ISP defect patterned (3,4) superlattice, the πz and πa bands at Y point are found to split into πz1, πz2, πa1, and πa2 bands. The bandgap Ez of the πz1 − πz2 band set and the one Ea of the πa1 − πa2 band set equal to each other. Both of them are however apart away from the Fermi level leaving the semimetal nature unchanged. In our band decomposed charge density studies of the split π-like bands at Y point, the πz1, πz2, πa1, and πa2 bands are found to correspond to four different bond groups as schematically illustrated in Fig. 3c.

Discussion

In the ideal free-standing silicene sheet, the sp2 and sp3 hybridization electronic configuration makes the Si-Si bonds in silicene to be same, whose π-like electrons would be thus high-symmetrically distributed along the bonds in the hexagonal honeycomb lattice. Therefore, the π-like bands are degenerate. By applying uniaxial strain on the silicene, the equivalence among the Si-Si bonds would be broken. As to the cases studied in Fig. 2, the 5% σz strain would make the πz bonds to elongate of 2.1% while the πa bonds only slightly contracts (~0.2%). The σa strain would induce the 3.0% elongation of πa bonds and 0.7% change of πz bonds. The different bond length changes along πa and πz bonds would result in different hopping integrals, which would then perturb the 3-fold homogeneously distributed electronic structure to split the π-like bands. The slight contraction (elongation) of bond length would induce the enhancing (weakening) of the binding strength of the band electrons to split the degenerate π-like bands, which stands for the increase and decrease of band energy interval of πa and πz bands presented in Fig. 2.

As studied in Fig. 3, by introducing a Si6 ISP defect into the repeated unit to pattern (3,4) silicene superlattice, the π-like bands are found to be split due to the defect induced perturbation. After contracting the Si6 hexagon to generate the ISP defect, the equivalence among the 3-fold homogeneously distributed Si-Si bonds is broken. In our studies, the πz1, πz2, πa1, and πa2 bands are calculated to gain 0.006, −0.011, −0.014, and 0.007 Å bond elongation on average as compared to the corresponding bond lengths of the defect free (3,4) PSS. According to the tight-binding method24, the bond elongation (contraction) would induce the decrease (increase) of the corresponding transfer integral. As a result, the π-like band splitting happens. The πa1 and πz2 bands are found to have lower band energies as compared to the πa2 and πz1 bands, respectively. The π band splitting was previously discussed in the 3p type superlattices which could be opened a mass bandgap to transfer the superlattices into semiconducting materials19,20,21,22. The intervalley scattering was proposed to understand the band gap opening. The periodically arranged defects could be approximately treated as introducing a periodic potential Vd( r ) to the pristine silicene. If the wavervectors of the opposite D and D′ valleys (the positions of the opposite Dirac cones) differ with each other by a reciprocal lattice G or mach with each other at a same point, the intervalley scattering would induce band splitting whose split energy interval Ed would be proportional to the perturbation related integration20.

where and are the Bloch functions of sublattice A at the opposite valley points D and D′. In the 3p type superlattices, such understanding of the band splitting could hold. However, in the 3p + 1 and 3p + 2 type superlattices, the wavevector between two nearest opposite Dirac points is failing to satisfy the above mentioned conditions. Providing we could talk about the 3-fold homogeneous equivalence of Si-Si bonds in silicene as bond symmetry, the band splittings happened in the strained defect-free silicene and the free-standing defect patterned superlattices may be then attributed to the bond symmetry breaking. Here, we would like to conclude the main contribution of our studies to the knowledge of bandstructure engineering of the two dimensional materials as compared to the previous studies19,20,21,22. We have carefully investigated the band splitting phenomenon of the π-like bands of the 3p + 1 and 3p + 2 type superlattices, which was missed in the previous studies. Furthermore, the corresponding band splitting mechanism could not be understood by the previously proposed intervalley scattering, which could be attributed to the bond symmetry breaking based on our detailed analysis. The split intervals are however apart away from the Fermi level to leave the semimetal nature unchanged. Fortunately, as to be discussed later in this paper, such energy intervals could be manipulated to approach each other to open a mass bandgap to transfer the silicene nanomesh to be semiconducting at the aid of uniaxial strain.

Now, we discuss the combination effects of strain and defect on bandstructure engineering. To shed light on the experimentally synthesized nanomeshes patterned by regularly arranged antidots, the Si12 antidot patterned silicene nanomeshes are examined as prototype in our studies, which corresponds to the vacancy hole formed after removing the Si12 nanoflake from silicene sheet. (In order to facilitate discussion, we would like to use the notation Sin to account for the antidot formed by removing a n-atom D6h silicon nanoflake from the silicene with the hole edge passivated by hydrogen.). Considering the reactivity of the dangling bonds, the vacancy hole edge would be ready for functional group adsorption in experimental studies. In this paper, the hydrogen atoms are used to saturate the dangling bonds to mimic the real nanomeshes to shed light on the experimental studies. After the hole edge hydrogenation, the silicene nanomeshes have been found to be nonmagnetic in our calculations. As to the silicene superlattices patterned by the antidots without dangling bond passivation, the resulted materials would be probably magnetic due to the presence of the unpaired π-like electrons on the hole edge, which have already been confirmed in the antidot studies of graphene21. The ferromagnetic coupling could keep the inversion symmetry while the antiferromagnetic one would break it, which are worthy of detailed studies. However, such studies are beyond our scope of this paper to understand the band splitting mechanism of the 3p + 1 and 3p + 2 nanomeshes. In Fig. 4, we use the (6,8) lattice as an example to illustrate our results. In Fig. 4a, the effects of σz strain on the (6,8) PSS are studied, which would shift the Dirac point toward Y point. At the strain of σz = 5.5%, the Dirac cone is found at the Y point. As to the Si12 antidot patterned (6,8) nanomesh studied in Fig. 4b, the π-like band splitting happens. The applied uniaxial strain σz would continuously lower the πa1 − πa2 band set toward the Fermi level, while it would lift the πz1 − πz2 band set. Once the Ea and Ez start to overlap, a mass bandgap straddle over Fermi level would start to form to transfer the nanomesh from semimetal to semiconductor. As presented in Fig. 4c, the critical value of uniaxial strain for such transition is found to be around 2% for the Si12 antidot patterned (6,8) nanomesh.

Figure 4
figure 4

The bandstructures of the free-standing (6,8) PSS and the ones under 3%, 5.5% σz strains (a) and the corresponding bandstructures for the Si12 antidot patterned (6,8) nanomeshes (b). The evolution of the mass bandgap as a function of the applied strain for the (6,8) nanomesh (c) and the relationship between Emax and lattice size N of (6,N) nanomeshes (d). The bandgaps of 3p-type nanomeshes are also presented in (d) for comparison.

Full size image

Furthermore, the mass bandgap could be continuously enlarged by enhancing strain until reaching its maximum Emax which equals to Ea (or Ez). Upon this point, it would get narrower when the strain σz further increases (see Fig. 4c). Based on our detailed calculations, we would like to conclude that the mass bandgap opening and the width tuning of such bandgap can be realized by applying uniaixal strain on all the 3p + 1 and 3p + 2 type (M,N) silicene nanomeshes. In our studies, we have also investigated the possibilities in tuning the Emax. The (6,N) nanomeshes are carefully studied. As shown in Fig. 4d, the Emax would reduce along with the increase of the lattice size N to reduce the density of the defect in silicene nanomesh.

In conclusion, we have carefully studied the silicene nanomeshes. Besides bandgap opening in the 3p nanomeshes which are transferred to be semiconducting due to the four-fold degeneracy removing, the inversion symmetry preserved defect can also induce band splitting in the other nanomeshes. However, the split gaps of πa-type and πz-type bands are apart away from the Fermi level leaving the semimetal nature unchanged, which fortunately could be shifted toward each other by applying uniaxial strain. Once they start to overlap, a mass bandgap would appear to transfer the nanomesh to be semiconducting, which could also be continuously enlarged until reaching its maximum Emax. Furthermore, the Emax could be tuned by controlling the defect density in silicene nanomesh.

Methods

We have performed first-principles calculations with the spin-polarized density functional theory by using the Vienna ab initio simulation package26. The interaction between ion and electron was described by the projector augmented-wave method27. The generalized gradient approximation with the Perdew, Burke, and Ernzerhof28 parameterized functional was used to account for the exchange-correlation energy among electrons. The wavefunction was constructed with the planewave basis set with the 250 and 400 eV cutoff energies for respectively dealing with the undoped pristine slicene-based nanostructures and the silicene nanomeshes patterned by the periodically arranged antidots. The method of the supercell was employed to simulate the two dimensional material by placing the sheet crystal in the XY plane which is separated by about 15 Å vacuum along the perpendicular direction to eliminate the interaction with its neighboring images. The convergence tolerances were 10−5 eV for the total energy and 0.01 eV/Å for the Feynman force acting on each aotm. The integration of electronic properties was calculated by using the Monkhorst-Pack technique29 to sample the Brillouin zone. Due to the small sizes, the structures studied with the primitive unit cell and the smallest rectangle unit cell were calculated with the 21 × 21 × 1 k-mesh. As to the orthogonal superlattices investigated in our studies, the sizes of the repeated units are 20.1 × 11.6 × 15 Å3 and 40.2 × 23.2 × 15 Å3, respectively. Accordingly, the k-meshes of 5 × 7 × 1 and 3 × 5 × 1 were used for studying their electronic properties.

Additional Information

How to cite this article: Jia, T.-T. et al. Silicene nanomeshes: bandgap opening by bond symmetry breaking and uniaxial strain. Sci. Rep. 6, 20971; doi: 10.1038/srep20971 (2016).