Abstract
The evolving shape of material fluid lines in a flow underlies the quantitative prediction of the dissipation and material transport in many industrial and natural processes. However, collecting quantitative data on this dynamics remains an experimental challenge in particular in turbulent flows. Indeed the deformation of a fluid line, induced by its successive stretching and folding, can be difficult to determine because such description ultimately relies on often inaccessible multi-particle information. Here we report laboratory measurements in two-dimensional turbulence that offer an alternative topological viewpoint on this issue. This approach characterizes the dynamics of a braid of Lagrangian trajectories through a global measure of their entanglement. The topological length  of material fluid lines can be derived from these braids. This length is found to grow exponentially with time, giving access to the braid topological entropy
of material fluid lines can be derived from these braids. This length is found to grow exponentially with time, giving access to the braid topological entropy  . The entropy increases as the square root of the turbulent kinetic energy and is directly related to the single-particle dispersion coefficient. At long times, the probability distribution of
. The entropy increases as the square root of the turbulent kinetic energy and is directly related to the single-particle dispersion coefficient. At long times, the probability distribution of  is positively skewed and shows strong exponential tails. Our results suggest that
is positively skewed and shows strong exponential tails. Our results suggest that  may serve as a measure of the irreversibility of turbulence based on minimal principles and sparse Lagrangian data.
may serve as a measure of the irreversibility of turbulence based on minimal principles and sparse Lagrangian data.
Similar content being viewed by others
Introduction
More than a century ago, O. Reynolds showed that watching the dynamics of coloured fluid lines in a flow was a powerful way to uncover the turbulent fabric of the underlying fluid motion1. This pioneering study provides a nice illustration that the problem of transport in turbulence is intimately connected to its Lagrangian description, the trajectory-based representation of hydrodynamics. Describing and characterizing Lagrangian properties of fluid turbulence is important for a better understanding of many natural and industrial processes, including turbulent mixing, the distribution of plankton in the ocean, or the spreading of pollutants in the atmosphere2,3. Despite the elegance of Reynolds approach, even now, unravelling the internal fluid motion in natural flows is not a trivial matter because the deformation of fluid lines is usually extremely convoluted3,4. This observation is not intrinsic to turbulence. Indeed, very complex patterns can be observed when a marker is advected in seemingly simple Stokes flows5,6, a phenomenon known as chaotic advection7. The “chaoticity” of the Lagrangian transport strongly hinders our ability to forecast the consequences of disasters such as volcanic eruptions or pollutant spills on the sea surface. Although basic Lagrangian quantities such as the single particle dispersion offer valuable information, there is a growing realization that multi-particle measurements are instrumental in better describing global transport properties of natural flows3,8,9,10.
The merger of ideas from Lagrangian hydrodynamics with those of dynamical systems has been a key route to unraveling the complexity of chaotic advection in periodic flows6,11,12,13. Crucially, it has been demonstrated that topological features of flows are not abstract mathematical concepts but are an essential part of fluid motion12,13,14,15. To date, the application of mathematical tools from topology or dynamical system theory has been largely restricted to idealized maps or simple flow configurations11,12,13,14.
Recent advances in laboratory modeling of turbulent flows, the development of experimental particle tracking techniques, as well as the availability of new mathematical methods have made it possible to extend the investigation to non-periodic and turbulent flows3,15,16,17,18,19,20,21. The combination of particle tracking velocimetry (PTV) and topological tools has recently offered insights into mixing, transition to chaos and irreversibility in flows4,22,23,24,25. However, when it comes to measuring key features of Lagrangian transport such as the long-time dynamics of fluid lines in turbulent flows26, experimental investigations still encounter numerous problems. Among them is the formidable task of describing the trajectories of many particles that become entangled with a growing complexity. Braid theory and the topology of surface mappings offer interesting means to tackle these questions6,14,26,27,28. It provides topological tools to measure the entanglement of braids made of Lagrangian trajectories. This approach is capable of capturing the deformation of fluid elements using topological considerations and a limited number of Lagrangian trajectories. The method is suitable for studying two-dimensional (2D) flows. So far, the potential of the braid method has been rarely investigated experimentally5,6,14,29,30,31.
Here, we report new experimental measurements of topological braids in 2D turbulent flows. Experiments have been carried out in a broad range of the turbulence kinetic energy by using both electromagnetically forced and Faraday wave driven 2D turbulence. The topological “length”  of material fluid lines is derived from the behavior of Lagrangian trajectories, measured using high-resolution PTV techniques. After a transient period, the statistical average of
of material fluid lines is derived from the behavior of Lagrangian trajectories, measured using high-resolution PTV techniques. After a transient period, the statistical average of  grows exponentially with time and its probability density function (PDF) becomes positively skewed with strong exponential tails. The braid entropy
grows exponentially with time and its probability density function (PDF) becomes positively skewed with strong exponential tails. The braid entropy  of the flow is measured. We show that
of the flow is measured. We show that  increases as the square root of the turbulent kinetic energy. This study also reveals that
increases as the square root of the turbulent kinetic energy. This study also reveals that  is directly related to the single-particle diffusion coefficient
is directly related to the single-particle diffusion coefficient  . Since quantifying the degree of irreversibility in turbulent flows32,33,34,35 is still a matter of active debate, our results suggest that
. Since quantifying the degree of irreversibility in turbulent flows32,33,34,35 is still a matter of active debate, our results suggest that  could be a promising alternative measure based on topological considerations and sparse Lagrangian data.
could be a promising alternative measure based on topological considerations and sparse Lagrangian data.
Results
The experiments are carried out in two different experimental setups used to produce homogeneous two-dimensional (2D) turbulent flows. First, we take advantage of the remarkable similarity between the horizontal motion of particles on the surface of a fluid perturbed by Faraday waves and the fluid motion in 2D turbulence17,18,19,20. Though the fluid particle motion has a vertical component, these similarities stem from the ability of Faraday waves to generate lattices of horizontal vortices17. These vortices interact with each other and fuel the turbulent motion. In these experiments, the Faraday wave driven turbulence (FWT) is formed on the water surface in a vertically shaken container. The forcing is monochromatic with a frequency set to  . Above a certain vertical acceleration threshold, parametrically forced Faraday waves appear with a dominant frequency of
. Above a certain vertical acceleration threshold, parametrically forced Faraday waves appear with a dominant frequency of  and a wavelength
and a wavelength  . Tracer particles move erratically in the wave field. The forcing scale of the horizontal fluid motion is roughly
. Tracer particles move erratically in the wave field. The forcing scale of the horizontal fluid motion is roughly  . In the second set of experiments, we generate electromagnetically forced turbulence (EMT) in a layer of electrolyte by running an electric current J across the fluid cell36,37. A spatially periodic vertical magnetic field B is generated by placing a matrix of magnetic dipoles underneath the cell. The Lorenz J × B force produces local vortices at the forcing wave number
. In the second set of experiments, we generate electromagnetically forced turbulence (EMT) in a layer of electrolyte by running an electric current J across the fluid cell36,37. A spatially periodic vertical magnetic field B is generated by placing a matrix of magnetic dipoles underneath the cell. The Lorenz J × B force produces local vortices at the forcing wave number  which fuel the turbulent motion. An important aspect of both methods is that energy is injected at an intermediate scale (determined either by the distance between the magnets37 or by the oscillon size17) in the wave number spectrum, leaving it to the inverse energy cascade to spread energy over a broad range of scales.
which fuel the turbulent motion. An important aspect of both methods is that energy is injected at an intermediate scale (determined either by the distance between the magnets37 or by the oscillon size17) in the wave number spectrum, leaving it to the inverse energy cascade to spread energy over a broad range of scales.
Eulerian energy spectra
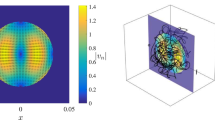
To visualize the horizontal fluid motion, the liquid-air interface is seeded with 50 μm diameter particles. The Eulerian velocity field is measured by using particle image velocimetry (PIV) techniques. Figure 1 shows wave number spectra of the horizontal kinetic energy measured in both experiments for different parameters. The spectral scaling is consistent with the Kolmogorov-Kraichnan prediction of  at wave numbers
at wave numbers  , revealing the presence of the inverse energy cascade38. At higher wave numbers,
, revealing the presence of the inverse energy cascade38. At higher wave numbers,  , some spectra follow the direct enstrophy cascade scaling
, some spectra follow the direct enstrophy cascade scaling  , while others are steeper, due to larger dissipation. The use of these two distinct methods allows us to study isotropic 2D turbulence in a broad range of kinetic energies,
, while others are steeper, due to larger dissipation. The use of these two distinct methods allows us to study isotropic 2D turbulence in a broad range of kinetic energies,  m2s−2 and forcing scales
m2s−2 and forcing scales  mm.
mm.
Two-dimensional turbulent flows: kinetic energy spectra measured by PIV.
(a) Electromagnetically driven flows (EMT): if the flow is weakly forced, forcing scale vortices interact weakly and the spectral energy is localized in a narrow wave number range about  . At higher forcing levels, vortices interact in the process of energy cascades and the energy spectrum spreads over a broad range of scales. A continuous Kolmogorov-Kraichnan spectrum is formed that shows a scaling of
. At higher forcing levels, vortices interact in the process of energy cascades and the energy spectrum spreads over a broad range of scales. A continuous Kolmogorov-Kraichnan spectrum is formed that shows a scaling of  at
at  . (b) Faraday wave driven flows (FWT): Kinetic energy spectra of the horizontal fluid motion. The forcing wave number
. (b) Faraday wave driven flows (FWT): Kinetic energy spectra of the horizontal fluid motion. The forcing wave number  can be changed easily by tuning the forcing frequency
can be changed easily by tuning the forcing frequency  at
at  ,
,  at
at  . (c) Energy spectra versus wave numbers normalized by the forcing wave number
. (c) Energy spectra versus wave numbers normalized by the forcing wave number  .
.
Topological braids and topological fluid loops
The turbulent fluid motion is also characterized here by using PTV which allows us to measure simultaneously the Lagrangian trajectories of hundreds of particles in the horizontal x-y plane17,18. A few examples of the 2D trajectories are shown in Fig. 2(a,d). In these experiments, tracer particles are tracked with high resolution for long times ( , where
, where  is the measured Lagrangian velocity autocorrelation time). We use tools from braid theory and the topology of surface mappings to characterize, in a topological sense, the deformation with time of fluid elements6,14,26,27,28,29. In the following, we broadly refer to these different tools as the braid description. This method is built upon basic topological considerations and a limited number of Lagrangian trajectories. The connection between Lagrangian trajectories and the topological description of fluid lines is based on two minimal assumptions: i) particles act as local mixers for the surrounding fluid and ii) fluid lines are impenetrable material objects. In physical terms, it emphasizes that the interaction of a fluid line with the stirring motion of surrounding particles determine completely its temporal evolution.
is the measured Lagrangian velocity autocorrelation time). We use tools from braid theory and the topology of surface mappings to characterize, in a topological sense, the deformation with time of fluid elements6,14,26,27,28,29. In the following, we broadly refer to these different tools as the braid description. This method is built upon basic topological considerations and a limited number of Lagrangian trajectories. The connection between Lagrangian trajectories and the topological description of fluid lines is based on two minimal assumptions: i) particles act as local mixers for the surrounding fluid and ii) fluid lines are impenetrable material objects. In physical terms, it emphasizes that the interaction of a fluid line with the stirring motion of surrounding particles determine completely its temporal evolution.
Physical and topological braids in FWT and EMT.
Two-dimensional fluid particles trajectories are tracked experimentally by using PTV techniques in the x-y plane for  in fully turbulent flows (a) driven by Faraday waves
in fully turbulent flows (a) driven by Faraday waves  or (d) electromagnetically forced
or (d) electromagnetically forced  . (b,e), Perspective view of the three-dimensional x-y-t strands (time is the third coordinate) built upon the 2D trajectories shown in (a,b). (b) also shows a 3D view of the surface elevation of the disordered Faraday wavefield measured at t = 0 s. (c,f), the physical braids obtained by the projection of the 3D strands onto the x-t plane. (g) Left. Schematics of a topological braid made of 3 Lagrangian trajectories. Right. Schematics of the temporal evolution of a topological fluid loop (blue line) entangled in the same braid. For clarity, the braid is represented as red, blue and green dots at the time of crossing of the 3 particle trajectories. The time evolution of the topological loop “length”
. (b,e), Perspective view of the three-dimensional x-y-t strands (time is the third coordinate) built upon the 2D trajectories shown in (a,b). (b) also shows a 3D view of the surface elevation of the disordered Faraday wavefield measured at t = 0 s. (c,f), the physical braids obtained by the projection of the 3D strands onto the x-t plane. (g) Left. Schematics of a topological braid made of 3 Lagrangian trajectories. Right. Schematics of the temporal evolution of a topological fluid loop (blue line) entangled in the same braid. For clarity, the braid is represented as red, blue and green dots at the time of crossing of the 3 particle trajectories. The time evolution of the topological loop “length”  is indicated (see Methods section for computation).
is indicated (see Methods section for computation).
In this approach, 2D trajectories are viewed as 3D strands, with time t being the third coordinate, Fig. 2(b,e). The 3D x-y-t trajectories are projected onto the x-t (or y-t) plane, Fig. 2(c,f). In this plane, trajectories create a physical braid made of over- and under-crossings of strands. The crossings are the key topological information upon which the braid description hinges. The crossings of trajectories in 2D turbulence are qualitatively illustrated in Fig. 2(c,f). The braid approach then relies on two distinct objects (Fig. 2(g)):
- the topological braid which is really the sequence of crossings of the trajectories previously described.
- the topological loop which is like a fluid ribbon entangled within the braid.
The topological braid is based only on the relative position of tracer particles and as such it does not require geometrical information such as the actual distance between strands (Fig. 2(g)_left panel and ref. 14). The topological loop can neither intersect itself nor pass through the braid (Fig. 2(g)_right panel). The degree of entanglement of the loop around the impenetrable strands of the braid can be quantified via a descriptor called the topological “length”  which is also referred to as the braiding factor (see details on the computation of
which is also referred to as the braiding factor (see details on the computation of  in Methods). In the course of time, each crossing along the braid distorts the loop and forces it to stretch or coil around the strands Fig. 2(g). If these deformations are irreversible, the degree of entanglement
in Methods). In the course of time, each crossing along the braid distorts the loop and forces it to stretch or coil around the strands Fig. 2(g). If these deformations are irreversible, the degree of entanglement  will increase. The time evolution of
will increase. The time evolution of  can be computed from the sequence of crossings in a given braid. The topological growth rate
can be computed from the sequence of crossings in a given braid. The topological growth rate  of the loop is expected to capture some features of the behavior of real material lines in a flow6,14.
of the loop is expected to capture some features of the behavior of real material lines in a flow6,14.
Braid entropy of 2D Turbulence
We measure the temporal evolution of the topological length  of the fluid loop in FWT and EMT. Measurements are carried out over a broad range of the turbulent kinetic energy of the flow,
of the fluid loop in FWT and EMT. Measurements are carried out over a broad range of the turbulent kinetic energy of the flow,  m2s−2 and for various forcing scales
m2s−2 and for various forcing scales  . The probability distribution function (PDF) of
. The probability distribution function (PDF) of  and the statistical mean
and the statistical mean  are estimated over at least 10 different braids and up to 100,000 initial topological loops.
are estimated over at least 10 different braids and up to 100,000 initial topological loops.
Figure 3 shows the PDF of  as a function of time at a flow kinetic energy
as a function of time at a flow kinetic energy  m2s−2. The initial loop is randomly entangled in the braid; as a consequence, at
m2s−2. The initial loop is randomly entangled in the braid; as a consequence, at  s the PDF is a Gaussian function. After a transient period, the PDF becomes skewed and develops strong exponential tail at large values of
s the PDF is a Gaussian function. After a transient period, the PDF becomes skewed and develops strong exponential tail at large values of  . No saturation in the growth of the exponential tail could be observed in the temporal observation window (up to 30
. No saturation in the growth of the exponential tail could be observed in the temporal observation window (up to 30  for some runs).
for some runs).
Figure 4 shows the temporal evolution of the statistical average  in FWT and EMT as the flow energy is increased. After a transient state,
in FWT and EMT as the flow energy is increased. After a transient state,  grows exponentially with time and its growth rate increases with the flow energy. This behavior was observed in all our experiments as long as a sufficient number of trajectories compose the braid. The time evolution of
grows exponentially with time and its growth rate increases with the flow energy. This behavior was observed in all our experiments as long as a sufficient number of trajectories compose the braid. The time evolution of  reflects the non-trivial nature of braids made of Lagrangian trajectories in 2D turbulence.
reflects the non-trivial nature of braids made of Lagrangian trajectories in 2D turbulence.
Topological length  of fluid lines in 2D turbulence.
of fluid lines in 2D turbulence.
Time evolution of  over the range of turbulent kinetic energy of the flow,
over the range of turbulent kinetic energy of the flow,  = (
= ( −
−  ) m2s−2 and for various energy injection scale
) m2s−2 and for various energy injection scale  . (a) FWT at
. (a) FWT at  Hz,
Hz,  mm, (b) EMT at
mm, (b) EMT at  mm, (c) FWT at
mm, (c) FWT at  Hz,
Hz,  mm, (d) FWT at
mm, (d) FWT at  Hz,
Hz,  mm, (e) FWT at
mm, (e) FWT at  Hz,
Hz,  mm. In (a–c),
mm. In (a–c),  is averaged over at least 15 different braids. Each braid is made of 80 different Lagrangian trajectories. In (d,e),
is averaged over at least 15 different braids. Each braid is made of 80 different Lagrangian trajectories. In (d,e),  is averaged over at least 10 different braids. Each braid is made of 60 different Lagrangian trajectories. Dashed lines are exponential fits.
is averaged over at least 10 different braids. Each braid is made of 60 different Lagrangian trajectories. Dashed lines are exponential fits.
To further characterize this complexity, we measure the braid entropy  as the growth rate of the logarithm of
as the growth rate of the logarithm of  at long times:
at long times:  ,
,  .
.  is closely related to the notion of topological entropy14. Its definition as the exponential growth rate of topological loops is inherited from the work of Thurston on surface mappings (see ref. 39 and references therein). Basically,
is closely related to the notion of topological entropy14. Its definition as the exponential growth rate of topological loops is inherited from the work of Thurston on surface mappings (see ref. 39 and references therein). Basically,  measures the evolution of the number of irreversible deformations that topological loops undergo in the flow.
measures the evolution of the number of irreversible deformations that topological loops undergo in the flow.
In these experiments,  increases as the square root of the flow kinetic energy
increases as the square root of the flow kinetic energy  , as shown in Fig. 5(a). We observe no appreciable difference between data collected in different experiments, suggesting that
, as shown in Fig. 5(a). We observe no appreciable difference between data collected in different experiments, suggesting that  is independent on both the turbulence generation method and on the details of the energy injection. In particular, we detect no dependence of
is independent on both the turbulence generation method and on the details of the energy injection. In particular, we detect no dependence of  on the energy injection scale
on the energy injection scale  . Figure 5(b) shows that the relation
. Figure 5(b) shows that the relation  is measured for a number of trajectories
is measured for a number of trajectories  in the braid as low as
in the braid as low as  .
.
Braid entropy  in 2D turbulence.
in 2D turbulence.
(a) The braid entropy  versus the turbulent flow energy
versus the turbulent flow energy  , where
, where  is the mean squared value of the horizontal velocity fluctuations.
is the mean squared value of the horizontal velocity fluctuations.  is computed over 10 different braids made of 80 trajectories each. (b)
is computed over 10 different braids made of 80 trajectories each. (b)  versus
versus  for a varying number
for a varying number  of trajectories that compose the braid. The dashed lines correspond to fit by a power law
of trajectories that compose the braid. The dashed lines correspond to fit by a power law  .
.
Discussion
Recently the concept of chaotic advection was further enriched by considering topological chaos6. The characterization of topological chaos hinges on the Thurston-Nielsen classification of surface mappings and on the concept of topological braids6,14,26. Our experimental work concerns topological chaos and explores the potential of the braid description to characterize 2D turbulence. For instance, Fig. 3 shows that the PDF of  presents growing exponential tails, a feature commonly associated with out-of-equilibrium systems.
presents growing exponential tails, a feature commonly associated with out-of-equilibrium systems.
The main results of this paper appear in Fig. 5(a), which shows that the braid entropy  is an increasing function of the flow kinetic energy
is an increasing function of the flow kinetic energy  , independent of the forcing scale of the turbulent flows. Moreover
, independent of the forcing scale of the turbulent flows. Moreover  grows as
grows as  with no sign of saturation. It is expected that the more particles are included in the braid, the better
with no sign of saturation. It is expected that the more particles are included in the braid, the better  approximates the stretching rate of a “real” fluid line14. Batchelor showed that the exponential growth of fluid line in homogeneous turbulence is governed by the deformation of the small fluid elements of which it is comprised26. To further test the robustness of our results, we have measured the exponential stretching rate of small fluid elements in our turbulent flows. We have used the finite time Lyapunov exponent method8 and found that the average exponential stretching rate
approximates the stretching rate of a “real” fluid line14. Batchelor showed that the exponential growth of fluid line in homogeneous turbulence is governed by the deformation of the small fluid elements of which it is comprised26. To further test the robustness of our results, we have measured the exponential stretching rate of small fluid elements in our turbulent flows. We have used the finite time Lyapunov exponent method8 and found that the average exponential stretching rate  of fluid elements follows:
of fluid elements follows:  , this result40 supports strongly the behavior for
, this result40 supports strongly the behavior for  observed in Fig. 5(a). It is quite remarkable that
observed in Fig. 5(a). It is quite remarkable that  can record the actual behavior of fluid elements from scarce Lagrangian data (in our measurements, as low as 30 trajectories for which the average inter-particle distance is larger than
can record the actual behavior of fluid elements from scarce Lagrangian data (in our measurements, as low as 30 trajectories for which the average inter-particle distance is larger than  ), while the computation of the Lyapunov exponents require high spatial resolution measurements of the entire velocity field.
), while the computation of the Lyapunov exponents require high spatial resolution measurements of the entire velocity field.
A recent study41 reported another type of entropy in 2D turbulent flows, namely the information entropy  . This entropy quantifies the complexity of turbulence in terms of its predictability. Measurements were performed in turbulent flows in soap films;
. This entropy quantifies the complexity of turbulence in terms of its predictability. Measurements were performed in turbulent flows in soap films;  was computed from Eulerian velocity fluctuations. In these experiments,
was computed from Eulerian velocity fluctuations. In these experiments,  was a decreasing function of
was a decreasing function of  . This is in sharp contrast with the behavior of
. This is in sharp contrast with the behavior of  which increases with
which increases with  in our work. This discrepancy highlights the fact that the relationship between the Eulerian and Lagrangian descriptions of turbulence remains an outstanding problem3,41. It also raises questions as to whether there are connections between different types of entropies in turbulent flows39,42.
in our work. This discrepancy highlights the fact that the relationship between the Eulerian and Lagrangian descriptions of turbulence remains an outstanding problem3,41. It also raises questions as to whether there are connections between different types of entropies in turbulent flows39,42.
 is a global topological quantity. Although it is connected to transport properties of the underlying flow, its connection to a “metric” descriptor of turbulent transport is not trivial. One of the most basic properties of Lagrangian trajectories is the single-particle dispersion
is a global topological quantity. Although it is connected to transport properties of the underlying flow, its connection to a “metric” descriptor of turbulent transport is not trivial. One of the most basic properties of Lagrangian trajectories is the single-particle dispersion  of a particle moving along the trajectory
of a particle moving along the trajectory  . In 2D turbulence, at long times, single-particle dispersion is similar to a Brownian motion and it reads:
. In 2D turbulence, at long times, single-particle dispersion is similar to a Brownian motion and it reads:  where
where  is the diffusion coefficient18,35. Recent experiments showed that
is the diffusion coefficient18,35. Recent experiments showed that  in 2D turbulence, where
in 2D turbulence, where  is the energy injection scale of turbulence18. The fact that
is the energy injection scale of turbulence18. The fact that  has therefore a remarkable consequence: the braid entropy
has therefore a remarkable consequence: the braid entropy  is a linear function of
is a linear function of  (see Fig. 6). Quantitatively, we have measured:
(see Fig. 6). Quantitatively, we have measured:  . The forcing scale
. The forcing scale  links a single-particle metric characteristic
links a single-particle metric characteristic  , to a multi-particle topological descriptor
, to a multi-particle topological descriptor  .
.
Although such a connection between single and multi-particle descriptors might sound surprising, it may originate from the uncorrelated motion of the particles that compose the braid. Indeed, we emphasize that the transition to the exponential growth regime of  is observed for time scales
is observed for time scales  (see Fig. 4). At these time scales, both the single18 and pair dispersion computed on the braided trajectories (with inter-particle distance being larger than
(see Fig. 4). At these time scales, both the single18 and pair dispersion computed on the braided trajectories (with inter-particle distance being larger than  ) show Brownian statistics. To our knowledge, there is as yet no theoretical understanding as to why the entanglement of independent Brownian trajectories results in an exponential growth of the topological length
) show Brownian statistics. To our knowledge, there is as yet no theoretical understanding as to why the entanglement of independent Brownian trajectories results in an exponential growth of the topological length  . We note that 2D turbulence plays an important role in this phenomenology since the r.m.s velocity
. We note that 2D turbulence plays an important role in this phenomenology since the r.m.s velocity  depends on the kinetic energy accumulated in the inertial range. The relation linking
depends on the kinetic energy accumulated in the inertial range. The relation linking  to
to  could be useful in oceanography to identify the energy injection scale
could be useful in oceanography to identify the energy injection scale  from Lagrangian data43.
from Lagrangian data43.
Much interest lies in determining Lagrangian tenets of turbulence irreversibility that would complement the Kolmogorov energy flux relations formulated in the Eulerian frame32,33,34,35. The braid entropy  is a promising topological measure of the irreversible deformation of fluid lines in 2D turbulence. On a practical note, the braid approach is particularly suitable for the analysis of natural flows in the ocean for which only sparse data are available. Much work is yet to be done to test the properties and potential applications of the braid entropy in fluid turbulence.
is a promising topological measure of the irreversible deformation of fluid lines in 2D turbulence. On a practical note, the braid approach is particularly suitable for the analysis of natural flows in the ocean for which only sparse data are available. Much work is yet to be done to test the properties and potential applications of the braid entropy in fluid turbulence.
Methods
Turbulence generation
In these experiments, turbulence is generated using two different methods. In the first, 2D turbulence is generated electromagnetically in stratified layers of fluid36. A 4 mm thick layer of an electrolyte solution (Na2SO4 water solution, SG = 1.03) is placed on top of a 4 mm thick layer of heavier (specific gravity SG = 1.8) non-conducting fluid (FC-3283). The fluid cell has a square section of 300 × 300 mm2. A matrix of 30 × 30 magnetic dipoles spaced in a checkerboard fashion 10 mm apart is placed under the bottom of the fluid cell producing spatially varying vertical magnetic field  . Electric current
. Electric current  flowing across the cell generates the Lorenz
flowing across the cell generates the Lorenz  force, which drives 900 horizontal vortices in the top (conducting) layer of fluid18,36,37. The interaction between these vortices, through the inverse energy cascade process, provides the energy that drives the turbulent flow. The bottom layer reduces the bottom drag and makes the flow in the top layer two-dimensional.
force, which drives 900 horizontal vortices in the top (conducting) layer of fluid18,36,37. The interaction between these vortices, through the inverse energy cascade process, provides the energy that drives the turbulent flow. The bottom layer reduces the bottom drag and makes the flow in the top layer two-dimensional.
In the second setup, Faraday surface waves are used to generate 2D turbulence19,20. The horizontal fluid motion on the surface of such parametrically excited waves shows strong similarities with the fluid motion in 2D turbulence. In these experiments, Faraday waves are formed in a circular container (178 mm diameter) filled with a liquid whose depth (30 mm) is larger than the wavelength of the perturbation at the surface (deep water approximation). An electrodynamic shaker is used to vertically vibrate the container. The forcing frequency  is monochromatic and is set to 30, 45, 60 or 110 Hz. The wavelength
is monochromatic and is set to 30, 45, 60 or 110 Hz. The wavelength  of the sub-harmonic Faraday waves is a function of
of the sub-harmonic Faraday waves is a function of  . We have recently demonstrated that Faraday waves can generate lattice of horizontal vortices whose characteristic scale is roughly
. We have recently demonstrated that Faraday waves can generate lattice of horizontal vortices whose characteristic scale is roughly  . The interaction between these vortices produces a turbulent flow. This method represents a versatile tool of laboratory modeling of 2D turbulence since Faraday wave turbulence can be produced in a broad range of kinetic energy level and forcing scales
. The interaction between these vortices produces a turbulent flow. This method represents a versatile tool of laboratory modeling of 2D turbulence since Faraday wave turbulence can be produced in a broad range of kinetic energy level and forcing scales  , by tuning either the vertical accelerations or the vibration frequency
, by tuning either the vertical accelerations or the vibration frequency  .
.
The use of these two laboratory-modeling methods allows us to study 2D turbulence in a broad range of kinetic energies  m2s−2 (
m2s−2 ( is the mean squared velocity fluctuations) and forcing scales
is the mean squared velocity fluctuations) and forcing scales  = (3.3–9.5) mm.
= (3.3–9.5) mm.
Flow characterization
The flows are visualized by placing 50μm diameter polyamide particles on the fluid surface. The use of surfactant ensures that particles do not aggregate on the surface and it facilitates the homogeneous spatial distribution of the particles. Videos are recorded at high frame rate (60 ~ 600 Hz) and a 16 bit resolution using the Andor Neo sCMOS camera. The flows are characterized using both particle image velocimetry (PIV) and particle tracking velocimetry (PTV) techniques. We use PIV to compute the Eulerian energy spectra of the flows shown in Fig. 1. The PIV velocity fields are computed on a 90 × 90 spatial grid (8 × 8 cm2 (FWT), 10 × 10 cm2 (EMT) field of view) with a time step of 0.008 s (FWT) or 0.033 s (EMT). The 2D Lagrangian trajectories used in the braid analysis are tracked by PTV techniques using a nearest neighbor algorithm17,18. In a highly turbulent flow (kinetic energy  m2s−2 and integral characteristic timescale
m2s−2 and integral characteristic timescale  s), hundreds of particles can be tracked simultaneously for 4 s at 120 fps over a 8 × 8 cm2 field of view.
s), hundreds of particles can be tracked simultaneously for 4 s at 120 fps over a 8 × 8 cm2 field of view.
The braid method
Topological fluid loops
In the course of time, each crossing along the braid distorts the topological loop and forces it to get more and more entangled in the impenetrable strands of the braid, see (Fig. 2g). It has recently been demonstrated that the level of entanglement of a loop can be described by a quantity  called “topological length” or braiding factor14.
called “topological length” or braiding factor14.  is equal to the number of times the loop crosses a imagined line (horizontal dashed line in Fig. 2(g)_right panel)) passing through all the particles that compose the braid at time
is equal to the number of times the loop crosses a imagined line (horizontal dashed line in Fig. 2(g)_right panel)) passing through all the particles that compose the braid at time  . Although it is named topological length,
. Although it is named topological length,  is a topological quantity that ultimately does not require the notion of “distance”. Its time evolution is completely described by the sequence of crossings along a braid.
is a topological quantity that ultimately does not require the notion of “distance”. Its time evolution is completely described by the sequence of crossings along a braid.
Experimental measurements
To compute the topological braids made of fluid tracers trajectories and their corresponding braiding factor  , we use tools from the braidlab library14,44 which have been modified to allow the computation to be carried out on a large number of trajectories. The analysis was performed over braids that are composed of
, we use tools from the braidlab library14,44 which have been modified to allow the computation to be carried out on a large number of trajectories. The analysis was performed over braids that are composed of  up to
up to  Lagrangian trajectories for which the inter-particle distance is larger than energy injection scale
Lagrangian trajectories for which the inter-particle distance is larger than energy injection scale  . The experimental capacities allow the computation of the single particle diffusion coefficient D and the braiding factor
. The experimental capacities allow the computation of the single particle diffusion coefficient D and the braiding factor  over large statistical samples (~3000 trajectories).
over large statistical samples (~3000 trajectories).
Additional Information
How to cite this article: Francois, N. et al. Braid Entropy of Two-Dimensional Turbulence. Sci. Rep. 5, 18564; doi: 10.1038/srep18564 (2015).
References
Reynolds, O. Study of fluid motion by means of coloured bands. Nature 50, 161–164 (1894).
Batchelor, G. K. An Introduction to Fluid Dynamics (Cambridge University Press, 1964).
Toschi, T. & Bodenschatz, E. Lagrangian Properties of particles in Turbulence, Ann. Rev. of Fluid Mech. 41, 375–404 (2009).
Kelley, D. H. & Ouellette, N. T. Separating stretching from folding in fluid mixing. Nat. Physics 7, 477–480 (2011).
Finn, M. D. & Thiffeault, J.-L. Topological optimization of rod-stirring devices, SIAM Review 53, 723–743 (2011).
Boyland, P. L., Aref, H. & Stremler, M. A. Topological fluid mechanics of stirring. J. Fluid Mech. 403, 277–304 (2000).
Aref, H. Stirring by chaotic advection. J. Fluid Mech. 143, 1–21 (1984).
Peacock, T. & Haller, G. Lagrangian coherent structures: the hidden skeleton of fluid flows, Physics Today, (February 2013); Haller, G. Lagrangian Coherent Structures, Ann. Rev. Fluid Mech. 47, 137–162 (2015).
Voth, G. A., Haller. G. & Gollub, J. P. Experimental measurements of stretching fields in fluid mixing, Phys. Rev. Lett. 88, 254501 (2002).
Amarouchene, Y. & Kellay, H. Conformation statistics of a deformable material line in two-dimensional turbulence. Phys. Rev. Lett. 95, 054501 (2005).
Ottino, J.M. Mixing, chaotic advection and turbulence. Ann. Rev. Fluid Mech. 22, 207–253 (1990).
Aref, H. The development of Chaotic Advection. Phys. Fluids, 14, 1315 (2002).
Ottino, J. M. The kinematics of mixing: stretching, chaos and transport, Cambridge University Press, Cambridge (1989).
Thiffeault, J.-L. Braids of entangled particle trajectories. Chaos 20, 017516 (2010).
Kleckner, D. & Irvine, W. T. M. Creation and dynamics of knotted vortices, Nature physics, 9, 253–258 (2013).
Villermaux, E. & Innocenti, C. On the geometry of turbulent mixing. J. Fluid Mech. 393, 123–147 (1999).
Francois, N., Xia, H., Punzmann, H., Ramsden, S. & Shats, M. Three-dimensional fluid motion in Faraday waves: creation of vorticity and generation of two-dimensional turbulence. Phys. Rev. X. 4, 021021 (2014).
Xia, H., Francois, N., Punzmann, H. & Shats, M. Lagrangian scale of particle dispersion in turbulence, Nat. Comm. 4:2013, doi: 10.1038/ncomms3013 (2013).
Francois, N., Xia, H., Punzmann, H. & Shats, M. Inverse energy cascade and emergence of large coherent vortices in turbulence driven by Faraday waves. Phys. Rev. Lett. 110, 194501 (2013).
von Kameke, A., Huhn, Fernández-García, F. G., Muñuzuri, A. P. & Pérez-Muñuzuri, V. Double cascade turbulence and Richardson dispersion in a horizontal fluid flow induced by Faraday waves. Phys. Rev. Lett. 107, 074502 (2011).
Punzmann, H., Francois, N., Xia, H., Falkovich, G. & Shats, M. Generation and reversal of surface flows by propagating waves. Nat. Phys. 10, 658 (2014).
Pine, D. J., Gollub, J. P., Brady, J. F. & Leshansky, A. M. Chaos and threshold for irreversibility in sheared suspensions. Nature. 438, 997 (2005).
Jeanneret, R. & Bartolo, D. Geometrically-protected reversibility in hydrodynamic Loschmidt-echo experiments, Nat. Comm. 5, 3474 (2014).
Afik, E. & Steinberg, S. Pair dispersion in a chaotic flow reveals the role of the memory of initial velocity. arxiv.org/pdf/1502.02818.pdf (2015).
Bourgoin, M., Ouellette, N. T., Xu, H., Berg, J. & Bodenschatz, E. The role of pair dispersion in turbulent flow. Science, 311, 5762 (2006).
Batchelor, G. K. The effect of homogeneous turbulence on material lines and surfaces. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 213, 1114 (1952).
Thurston, W. On the geometry and dynamics of diffeomorphisms of surfaces. Bull. Am. Math. Soc. 19, 417 (1988).
Caussin, J.-B. & Bartolo, D. Braiding a flock: winding statistics of interacting flying spins. Phys. Rev. Lett. 114, 258101 (2015).
Allshouse, M. R. & Thiffeault, J.-L. Detecting coherent structures using braids. Physica D 241, 95–105 (2012).
Puckett, J. G., Lechenault, F., Daniels, K. E. & Thiffeault, J.-L. Trajectory entanglement in dense granular materials, J. Stat. Mech., P06008 (2012).
Filippi, M., Atis, S., Thiffeault, J.-L., Allshouse, M. & Peacock, T. Untangling tracer trajectories and clarifying coherence in 2D flows using braid theory, Bull. Am. Phys. Soc. 59, 20 (2014).
Xu, H., Pumir, A., Falkovich, G., Bodenschatz, E., Shats, M., Xia, H., Francois, N. & Boffetta, G. Flight-crash events in turbulence, PNAS, 111, 21 (2014).
Jucha, J., Xu, H., Pumir, A. & Bodenschatz, E. Time-reversal-symmetry breaking in turbulence. Phys. Rev. Lett. 113, 054501 (2014).
Frishman, A. & Falkovich, G. New type of anomaly in turbulence. Phys. Rev. Lett. 113, 024501 (2014).
Xia, H., Francois, N., Punzmann, H. & Shats, M. Taylor particle dispersion during transition to fully developed two-dimensional turbulence, Phys. Rev. Lett. 112, 104501 (2014).
Xia, H., Shats, M. & Falkovich, G. Spectrally condensed turbulence in thin layers, Phys. Fluids 21, 125101 (2009).
Byrne, D., Shats, M. & Shats, M. Robust inverse energy cascade and turbulence structure in three-dimensional layers of fluid, Phys. Fluids 23, 095109 (2011).
Kraichnan, R. Inertial ranges in two-dimensional turbulence, Phys. Fluids 10, 1417 (1967).
Budisic, M. & Thiffeault, J.-L. Finite-time Braiding Exponents. Chaos 25, 087407 (2015).
Xia, H., Francois, N., Punzmann, H., Szewc, K. & Shats, M. submitted for publication.
Cerbus, R. T. & Goldburg, W. I. Information content of turbulence. Phys. Rev. E 88, 053012 (2013).
Dorfman, J. R. An introduction to chaos in nonequilibrium statistical mechanics Cambridge University Press (1999).
LaCasce, J. H. Statistics from Lagrangian observations. Progr. Oceanogr. 77, 1–29 (2008).
Thiffeault, J.-L. & Budisic, M. Braidlab: A software package for Braids and Loops, arxiv.org/abs/1410.0849 (2015).
Acknowledgements
This work was supported by the Australian Research Council’s Discovery Projects funding scheme (DP150103468). HX acknowledges the support by the Australian research Council’s Future Fellowship (FT140100067). BF acknowledges support by the National Science Foundation under Grant No. 1515202.
Author information
Authors and Affiliations
Contributions
N.F., H.P., H.X. and M.S. designed and performed experiments. N.F., H.X. and B.F. analysed the data. N.F. wrote the paper. All authors discussed and edited the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Francois, N., Xia, H., Punzmann, H. et al. Braid Entropy of Two-Dimensional Turbulence. Sci Rep 5, 18564 (2016). https://doi.org/10.1038/srep18564
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep18564
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

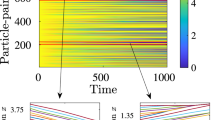




 at fixed flow energy
at fixed flow energy  . The PDFs are averaged over 15 different braids (made of 80 trajectories) and statistics are collected over 100,000 topological loops.
. The PDFs are averaged over 15 different braids (made of 80 trajectories) and statistics are collected over 100,000 topological loops.


 in this graphics are made of
in this graphics are made of  trajectories.
trajectories.