Introduction

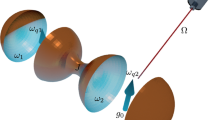
Quantum technologies are expected to bring great benefits to many human endeavours in the not-too-distant future. In the past decades it was shown that devices exploiting the laws of quantum mechanics can in principle cross boundaries that classical devices cannot. Advanced systems such as quantum memories and quantum computers are being developed in an effort to realise these transformative quantum technologies1. In addition to the practical aspects of quantum technologies, there is great interest in viewing quantum information processing as a fundamental description of Nature. This leads naturally to the question of how quantum information processing is affected by relativistic motion2. Here, we ask the question of how the relativistic motion of a cavity mirror can be used to achieve a quantum state inside the cavity that can in principle be used for quantum computation. We show that we can create such a universal resource state in the continuous variables defined by the quadratures of the field modes inside the cavity. This proposal can be implemented practically using superconducting circuits (see Fig. 1).

Figure 1
figure 1

Schematic of the physical setup.

(a) Cluster states on optical modes in a cavity with a moving mirror. The dynamical Casimir effect due to the accelerated motion of the mirror generates two-mode squeezing in the cavity modes. (b) Creating cluster states in a superconducting circuit: the time-varying current changes the flux through the SQUID, leading to a dynamical Casimir effect equivalent to that in (a).

Full size image

Recently, it was shown that relativistic motion can be used to generate bipartite quantum gates. In particular, two-mode squeezing3 and beam-splitting gates4 between field modes were implemented through the non- uniform acceleration of a cavity. A promising experimental realisation of these scenarios is circuit Quantum Electrodynamics (cQED), where Superconducting Quantum Interferometric Devices (SQUIDs) provide tuneable boundary conditions corresponding to mirrors moving at speeds close to the speed of light in the medium. This possibility was exploited for the first experimental observation of the Dynamical Casimir Effect, i.e., particle creation through relativistic motion of boundary conditions5,6. We note that the beam-splitting gate was recently experimentally demonstrated in this type of system7 and that two-mode squeezing involving two distinct cavity modes has also been achieved in cQED8. Moreover, some of us have shown that the same phenomenon originates an observable effect in the fidelity of quantum teleportation between two superconducting cavities, one of them undergoing a temporal variation of the boundary conditions9. These works open a new avenue of research on the effects of relativistic motion and gravity in generic quantum technologies and in particular quantum computing with continuous quantum variables. While it is possible to transfer the continuous-variables entanglement generated in the Dynamical Casimir Effect to discrete-variables systems such as qubits10 the analysis of relativistic effects in qubits is typically limited by the impossibility of achieving relativistic velocities -which can only be accessed in a quantum simulator11.

Quantum computation with continuous variables (CV) has attracted a great deal of attention as an alternative to the traditional qubit approach to quantum computing12 and the CV version of measurement-based quantum computing is well-developed13,14,15,16. In this paradigm for quantum computing the quantum gates are implemented by measurements on a particular type of multipartite entangled state known as a cluster state. Assuming that we can implement the required measurements (via homodyne detection and photon counting17), these states are universal for quantum computation. A practical way to create CV cluster states in a cavity using non-relativistic methods is by creating an entangled optical frequency comb18, a proof-of-principle experiment of which was recently performed19.

In this paper we show how to generate large CV regular cluster states through the relativistic accelerated motion of a cavity. The quantum field inside the cavity is initially in the vacuum state. We exploit entanglement resonances among different modes of the cavity3 to show that, by suitably choosing the motion of the boundaries, it is possible to generate specific multimode entangled states. These states can always be transformed into regular CV cluster states by suitably phase-shifting some of the modes. We propose a specific implementation with superconducting cavities in which the motion of the boundary conditions is implemented through tunable SQUIDs. In particular, we show an example with four modes that is within reach of current technology. In this way, we also contribute to transferring the concept of measurement based quantum information processing using continuous variables to the field of cQED.

In the Methods section we will review the technical tools required to describe quantum fields in relativistically moving cavities. In the Results section we show how to produce CV cluster states using relativistic motion and we present an experimental implementation in superconducting circuits. We conclude our paper with a discussion of our results.

Methods

Technical tools: quantum fields confined within moving cavities

In this section we review the technical tools to describe relativistic quantum fields, following mainly ref. 3 unless stated otherwise. We consider that the length of the cavity is constant in the reference frame of an observer co-moving with the cavity. Using the covariance matrix formalism, we show how to use entanglement resonances to create a two-mode squeezing gate in the case the motion is either discrete or continuous. Finally, we show that the gates can also be produced in case a single cavity wall oscillates.

Field quantization within a cavity

We consider a massless field confined within a 1 + 1 cavity in flat space-time, which can be employed to model a single polarisation-mode of light20. We use Minkowski coordinates which are a convenient choice to describe the field when the cavity undergoes inertial motion (in this work the signature is (−, +)). The left and right boundaries of the cavity are initially at positions and respectively, where , the length of the cavity is L :=  and we impose Dirichlet boundary conditions at the walls of the cavity, i.e. . When the cavity is inertial, the mode solutions to the Klein-Gordon equation form a discrete set and take the form

where the Minkowski frequencies are defined as and the modes satisfy the eigenvalue equation

The field can be expanded as

where the operators are bosonic operators which satisfy the canonical commutation relations and define the vacuum by for all .

We consider that at the cavity undergoes a period of uniform acceleration. Our formalism can be used to describe both discrete and continuous changes in acceleration. Rindler coordinates are a suitable choice to describe the cavity during periods of accelerated motion. The transformation between Minkowski and Rindler coordinates is given by

where has dimensions of length and is the dimensionless Rindler time coordinate. The proper acceleration of an observer moving along a trajectory is . A crucial point is that we consider that the cavity length is constant with respect to this observer. The observer’s proper time τ is related to the Rindler time coordinate by . Thus we can write , and as has been done in3. The solutions to the Klein-Gordon equation in Rindler coordinates take the form

where the Rindler frequencies are defined as . The Rindler modes satisfy the eigenvalue equation

During the periods of uniform acceleration, the field can be therefore expanded in these coordinates as

where the annihilation operators define the Rindler vacuum by for all and satisfy the canonical commutation relations .

Bogoliubov transformation

It is well known that the vacua and are different21. This implies that an accelerated observer will disagree with an inertial one that the state is devoid of particles. This fundamental observation is at the basis of the most exciting phenomena predicted by quantum field theory in curved spacetimes—such as dynamical Casimir effect and Unruh-Hawking effect—and is also responsible for relativistic effects in Quantum Information tasks between moving observers9.

We now briefly review the techniques introduced in refs 22,23 to study quantum information in cavities undergoing relativistic motion. The mode solutions to the Klein-Gordon equation in Minkowski and Rindler coordinates are related by the following Bogoliubov transformations21,

where the coefficients of the infinite-dimensional matrices and are defined by

and is the conserved inner product, see Ref. 21. Therefore, the induced transformation between the bosonic operators is

The Bogoliubov coefficients account for particle creation, while account for mode mixing. It is possible to compute analytically the inner products in Eq. (9) by expanding the Bogoliubov coefficients in terms of a dimensionless parameter , as was done in22 and one obtains

where the superscripts stands for the corresponding order in the perturbative expansion. Notice that the zero order coefficients are diagonal and can be written as .

The explicit expression of the first contributions to (11) can be found in ref. 22. The Bogoliubov coefficients and correspond to instantaneous changes between inertial and uniformly accelerated motion. A general cavity trajectory can be described as a succession of such transformations followed by periods of free evolution during which the field modes acquire phases and for inertial and uniformly accelerated free evolution respectively22,23. Notice that . The modes of a cavity at rest and the modes of the cavity after any trajectory are related by a general Bogoliubov transformation of the form (8), where the transformation matrix is

the Bogoliubov matrices A and B are functions of the Minkowski-Rindler instantaneous Bogoliubov coefficients and the phases acquired during the periods of free evolution. The exact expression depends on the travel scenario chosen22.

Covariance Matrix formalism

We use the covariance matrix formalism which is particularly convenient when one needs to apply quantum information techniques to quantum field theory23. In this formalism, which is applicable to bosonic fields in Gaussian states, all the relevant information about the state is encoded in the first and second moments of the field. In particular, given a collection of N bosonic modes, we can collect the second moments in the Covariance Matrix σ defined by the elements , where denotes the expectation value with respect to the state of the field and the quadrature operators are the generalized position and momentum operators of the field modes. In this paper we follow the conventions used in ref. 23, where the operators for the n-th mode are given by

and .

The covariance matrix formalism enables elegant and simplified calculations and has been proven useful to define and analyze computable measures of bipartite and multipartite entanglement for Gaussian states12.

Every unitary transformation U in Hilbert space that is generated by a quadratic Hamiltonian can be represented as a symplectic matrix S in phase space. These transformations form the real symplectic group , the group of real matrices that leave the symplectic form Ω invariant, i.e., , where the symplectic form takes the expression and

The time evolution of the field, as well as the Bogoliubov transformations, can be encoded in this structure. The symplectic matrix corresponding to the Bogoliubov transformation in Eq. (8) can be written in terms of the Bogoliubov coefficients as

where the are the 2 × 2 matrices which have the explicit form

The covariance matrix after a Bogoliubov transformation is given by . Let us assume that we are only interested in the state of two modes k and after the transformation. A great advantage of the covariance matrix formalism is that the trace operation over a mode is implemented simply by deleting the row and column corresponding to that mode. In the next subsection, we will apply this formalism to compute the transformed state of an initial vacuum of the field when the cavity undergoes motion of the boundary conditions.

Entanglement resonances and two-mode squeezer gates

When a cavity undergoes nonuniform motion, entanglement is created between every pair of modes3. Furthermore, the entanglement between chosen couples of modes can be selectively enhanced by “resonances”. An entanglement resonance is a linear increase of entanglement proportional to the number of times a particular travel scenario is repeated3,4,22,24.

There are two different kinds of entanglement resonances in the system. The first is connected to particle creation and leads to a two-mode squeezing gate3. Particle creation resonances have been extensively studied in the context of the dynamical Casmir effect6. The second entanglement resonance is produced by mode mixing without particle creation, which implements beam splitting gates4. In this work we will exploit particle creation resonances, since the squeezing gates which can be produced by them are a useful resource for the generation of cluster states16.

Let us consider that the field is initially in the vacuum state. The covariance matrix in this case is the identity matrix in dimensions where M is the number of modes. The cavity then undergoes N identical intervals of uniform acceleration, each of them of duration

Here is the the frequency of mode n. The reduced covariance matrix of two oddly-separated modes k and is obtained by tracing over Eq. (14) yielding,

where with and is the Pauli matrix. The matrix corresponds to a two-mode squeezed state with squeezing parameter . It is possible to define an effective Hamiltonian which gives rise to such state,

with as defined in Eq. (13). It is possible to generate high degrees of entanglement by increasing the number N of repetitions reaching squeezing degrees as high as . However, for large N second order terms in the Bogoliubov series expansion, which are proportional to , can no longer be neglected. These terms introduce thermal noise in the two-mode squeezed state having negative effects in the preparation of the cluster state. However, in the section “Continuous sinusoidal motion: Experimental scenario’’ we will show that a cluster state containing significant amounts of squeezing and entanglement can be generated with realistic experimental parameters.

Discrete and continuous motion

The entanglement created at first order in h between any two modes with different quantum number after any travel scenario is proportional to the first order correction to beta coefficient , see ref. 23. In the case of sharp onsets and offsets of acceleration, the coefficient is in turn proportional to the inertial-to-uniformly-accelerated first order correction :

All the above can be generalised to the case of accelerations that change continuously. In particular, if the cavity moves with a sinusoidal oscillation at a frequency , then resonances appear for all the oddly separated modes that satisfy . The formalism for the case of a rigid cavity that oscillates as a whole can be found in ref. 4. Notice that the timescale involved in the changes of acceleration must be comparable to the characteristic timescale of the cavity, i.e. .

A single oscillating cavity wall

Next, we consider the case in which only one wall of the cavity is oscillating with frequency , where . The Bogoliubov coefficients for this case can be computed using a perturbative expansion where now

is the perturbation parameter. That is, we are assuming small oscillations, as in the dynamical Casimir effect experiment6. Notice that in harmonic motion, the maximum acceleration is given by . Therefore, our parameter is given by

The Bogoliubov coefficients for this case are found in ref. 25. In particular, assuming that the time T of the oscillation is long enough,

we find that the beta coefficients are given by

where is the Kronecker delta.

CV cluster states

Cluster states are a particular type of multipartite entangled state that, together with potentially simple measurements, are universal for quantum computation26. In the case of cavities, information can be encoded in the cavity field modes which are quantum continuous variables (CV)13,14. In this section we review the stabiliser formalism for CV cluster states and its relationship with two-mode squeezing operations.

The Stabiliser Formalism for CV cluster states

A particularly powerful and efficient way to describe cluster states is via the stabiliser formalism27. In this technique, a quantum state is described completely by a set of n operators , called stabiliser operators, of which is an eigenstate with eigenvalue +1:

The stabiliser operators generate an Abelian group of cardinality . All the members of this group stabilise .

For continuous variables, the individual information carrying systems are quantum field modes or quantum harmonic oscillators. We can define the Heisenberg-Weyl operators

where are the continuous variables and Q and P the canonical position and momentum operators of the system. The stabiliser operator for a squeezed field mode j can then be written as28

where is the squeezing strength, with r the squeezing parameter. The single operator fully determines the quantum state of mode j. When the field mode j is in the vacuum state . The controlled-phase gate between two modes j and k is given by the operator

We can formally create continuous-variable cluster states by preparing a set of modes in momentum-squeezed states with and applying the controlled-phase gate between all the modes that we wish to entangle. This creates new stabiliser operators

Expressing this in exponential form using Eq. (25) then leads to the stabiliser condition for cluster states

where and and A is the adjacency matrix for the cluster. However, ideal continuous-variable cluster states that satisfy Eq. (29) are unphysical and there are various inequivalent ways to approach these states. While the generation based on the controlled-phase gates is conceptually the simplest way to generate CV cluster states, from a physical point of view the required entanglement is easier created using two-mode squeezing. We can write a two-mode squeezing operator as

Using the Bloch-Messiah reduction29, a general multi-mode squeezing operator can then be constructed (up to local phase shifts) according to

where t is the interaction time and is a bilinear interaction Hamiltonian

Such a Hamiltonian leads to a complex adjacency matrix for a graph state30

where we used that in our case . The matrix defines a undirected graph called an H-graph that approaches a CV cluster state up to local phase shifts in the mathematical limit . In particular a succession of commuting two-mode squeezing operations of equal squeezing parameter generates an H-graph state which is bipartite, that is, all the nodes in the graph can be split into two sets such that the two-mode squeezers only relate the elements of one set with the elements of the other. By introducing phase shifts on the elements of one set, the H-graph state is transformed into a continuous variable cluster state16. As we will see in detail in the Results section, in the superconducting circuit scenario that we consider in this paper the phase shift is implemented by a rotation of the same pump that generates the two-mode squeezing. For the sake of simplicity, in the remainder of the paper we will focus on how to generate the H-graph state itself, assuming that appropriate rotations of the pump can always be implemented. We will assume that all the two-mode squeezing operations commute, which is an exact result up to the first order in h. Recalling Eqs. (17) and (18) and comparing them with Eqs. (32) and (33), we find that a succession of commuting two-mode squeezing operations generates a matrix which is proportional to the first order terms of the Bogoliubov coefficients. The role of the second order deviations from the ideal scheme will be discussed in detail in the Results section. Cluster states can be diagrammatically represented by a graph in which each node corresponds to a party and the edges between nodes represent entanglement.

Results

In this section we show how to produce a CV Gaussian cluster state through motion of the cavity. In principle, arbitrarily large grids of entangled modes can be achieved. We will also discuss possible limitations.

Step one: establishing bipartite links

We start by choosing an odd prime number . As we will discuss later, this choice allows for a more symmetric definition of the state. We then choose two modes that satisfy . We then notice that the first order correction to the Bogoliubov beta coefficient of an arbitrary trajectory is proportional to

Once p is fixed, we see that achieves a maximum for the couple of modes and and takes the value .

In the following, we list the operations needed to create the multipartite entangled state i.e., we describe the motion of the boundaries in terms of total time of travel scenario. The cavity undergoes an arbitrary travel scenario that lasts a total proper time

As found in ref. 3 and explained above, all pairs of modes that satisfy will have an entanglement resonance. At this early stage of the protocol we must notice that, unfortunately, the same happens also for all the couples of modes which satisfy where . In fact, for any q there are combinations of l and for which we obtain

and therefore, all these extra couples of modes also undergo an entanglement resonance. Note that q must be an odd number since must be odd and thus, no entanglement is generated to first order in h. We notice though that for these extra modes

which in general means that, already for , the coefficient is approximatively 3% of the value of (which has q = 1).

We can repeat the travel scenario any number of times in order to linearly increase the entanglement between the modes. This allows us to engineer entanglement between the following modes:

Here, all double arrows represent the (“large”) entanglement created between two modes. This entanglement is shown in Fig. 2 as vertical black edges.

Figure 2
figure 2

The CV H-graph state generated by the travel scenario described in the text.

The vertical edges are created by , the solid grey diagonal edges by and the dashed edges by . This creates a ladder graph.

Full size image

Step two: creating a chain of entangled modes

We next proceed to increase the entanglement links in (38) and let the cavity undergo a new travel scenario with total proper time

which will entangle all couples of modes which satisfy . We can again repeat the travel scenario any number of times to achieve appreciable entanglement between the modes

Again, the double arrows indicate entanglement and is shown in Fig. 2 as diagonal dashed grey edges.

Step three: creating ladders of entangled modes

Following the reasoning above, we now choose a final travel scenario with total proper time

Once the travel scenario is repeated the necessary amount of times one achieves the multipartite state of the form

This entanglement is shown in Fig. 2 as diagonal solid grey edges. The resulting H-graph has a ladder configuration. The mode p itself does not participate in the graph state.

Selecting contributing entangled modes

In the previous section we have achieved a multipartite entangled state which has the ladder structure shown in Eq. (42) and Fig. 2. We have already noted that the entanglement between pairs of modes in Eq. (42) is not the same as quantified by . We would like to have a state where each entangled pair of modes exhibits the same amount of entanglement.

Since the aim is to obtain a multipartite state with entanglement between modes that forms a particular structure, we need to guarantee that the entanglement between the modes in the structure is much higher than the entanglement with other modes. For this reason, we have chosen a large prime number and we keep all pairs of modes that satisfy

where sets a limit on the minimum amount of entanglement which we want to generate. The value of sets the minimum value of k -denoted by - that we consider and the corresponding number of mode pairs, which is given by:

Notice that every time the cavity undergoes some travel scenario, will depend on the prime p and will be different for different sets of modes. In addition, we have chosen numbers . Clearly, for the bounds will be identical given a choice of . We can therefore rewrite (42) as

If is chosen tight enough, all modes in Eq. (45) will share almost the same amount of entanglement.

Step four: “Propagating” the entanglement

In this subsection we show how to propagate the entanglement from the basic structure we have built in Eq. (42) and Fig. 2, to build a regular structure.

Enlarging the structure of the multipartite state

We have shown how we can create an H-graph state in which the modes are entangled according to a ladder topology (a ladder graph). We will now proceed to show how to extend the ladder graph to a square lattice graph. We choose another prime and . Since would allow for substantially different amounts of entanglement, we choose a prime of the same order of magnitude as p. Among the modes that will be entangled in the ladder graph generated by p there will be a mode that coincides with mode of in the ladder graph generated by (with . If the mode are within the ranges defined by and , then we can use the travel scenari with total proper time

Without loss of generality, we can assume that . Therefore

where we do not specify the endpoint of the chain because it now depends on and . We now choose another prime and and repeat the above process to get the structure

The aim will now be to close all the links and complete the lattice of entangled modes.

Final step

To complete our scheme, we notice that

which are both odd numbers. This again guarantees that the entanglement is created at first order in . We now let the cavity undergo two travel scenarios with proper times

We therefore obtain our final state:

See an example in Fig. 3. So far, we have shown that, in principle, is possible to generate a large square lattice of entangled quantum field modes within a cavity. Technically, this means that we have generated an H-graph with the structure of a square. Dividing the graph in two sets such that the edges of the graph only relate elements of one set with elements of the other and applying phase shifts on the elements of one set, the complex adjacency matrix of the H-graph state -see Eq. (33)- is transformed into the adjacency matrix of a CV cluster state16. In general, the resulting CV cluster state does not have the same form as the original H-graph, except in those cases where the adjacency matrix A is self-inverse16,31. An interesting example is a four-mode square H-graph -with one minus sign in the adjacency matrix- which is then transformed into a square CV cluster state after the phase shifts16,31. In the next section we will show that this example is within reach of current technology in circuit QED.

Figure 3
figure 3

H-graph state for p = 29, and , with and .

Each mode, indicated by an open circle, has potentially multiple labels, associated with p, , or .

Full size image

Continuous sinusoidal motion: Experimental scenario

We have developed a scheme to prepare CV cluster states. We now propose a simple implementation that can be achieved with current technology. The aim is to build up a quadripartite state. We choose superconducting cavities, where the boundary of the field can be controlled by external magnetic fluxes32,33,34. A similar system—with only one wall—has been successfully exploited in the first experimental demonstration of the dynamical Casimir effect6.

Let us consider now a resonator in which one of the walls is a tunable SQUID32. The spectrum is given by

The frequency of the fundamental mode is GHz. For the sake of convenience, we focus on a set of modes within the range of frequencies where linear amplifiers operate. We start by driving the SQUID at . We therefore obtain

We then drive the system at , entangling modes 2 and 3. Therefore

The state (55) is a multipartite entangled state. Entanglement can be extended to form a larger regular structure by means of the techniques described in this work. Within the approximations commented in, the section “Discrete and continuous motion” higher order entanglement resonances are completely suppressed. The time of the oscillation can be suitably chosen in order to generate a similar amount of entanglement between all the links (see Fig. 4). In particular, the reduced state of modes and after the first drive is given by

Figure 4
figure 4

Logarithmic negativity vs. time of the oscillatory motion for modes k = 2 and (solid, blue), and (dashed, red), and (dotted, yellow) and and (dash-dotted, green).

, .

Full size image

For small h the state of the system remains pure to first order corresponding to a two-mode squeezed state with squeezing parameter . However, when repeating the trajectory a large number of times to generate a resonance, second order terms in the expansion of the Bogoliubov coefficients need to be included. These second order terms give rise to thermal noise quantified by which in this case is given by Eq. (23). A similar expression holds for modes and after the first drive. The entanglement in state (56) can be quantified with the logarithmic negativity which yields in this case:

and similarly for . Now we can drive the system at in order to entangle modes and . However, the initial state is no longer the vacuum. After the first drive the reduced covariance matrix of modes and is

where and . The second drive transforms the state into

where the matrices above have the expression

Note that if the amount of squeezing and entanglement generated with the first drive were exactly the same, i.e. , then the state would be

The fact that adds a source of imperfection. The logarithmic negativity of the state in Eq. (59) is

Two drives suffice to build up a linear graph. A third drive at would entangle modes and , closing the square. In this case, the entanglement would be given by a similar expression as in Eq. (62), replacing by . Figure 4 shows that a significant amount of entanglement is generated among the selected pairs of modes. The time of the drives can be chosen in such a way that all the pairs share a similar degree of entanglement. With all the above we have generated a H-graph state with square structure. Now, if we consider a rotation of the pump by an angle θ in one of the drives, say the last one, the corresponding correlation operators are transformed to , . Thus, for , the corresponding two-mode squeezing operator acquires a minus sign. The effect is completely equivalent to replace by . Therefore, the effective Hamiltonian acquires the form of the adjacency matrix of a square cluster state16. A square cluster state is a universal resource for measurement-based quantum computation, provided that homodyne detection and photon-counting are possible. Both techniques are within reach of current circuit QED technology35,36.

Discussion

We have shown that it is possible to generate continuous-variable cluster states on electromagnetic cavity modes by choosing a suitable relativistic motion of the cavity. The entanglement grows linearly in time. The size of the lattice is determined by the choice of initial driving frequency, the amount of entanglement required between every mode and the desired length-to-height ratio of the square cluster. As a first experimental implementation, we propose a simple example of a four-mode square cluster state in a superconducting resonator with tuneable boundary conditions. This scheme is within reach of current circuit QED technology and would be the first demonstration of a multipartite continuous variable cluster state in cQED. An interesting avenue of research would be the extension to regimes of high squeezing levels, such as the ones required for fault-tolerant quantum computing with CV cluster states37. In brief, our main contribution is to implement cluster states in relativistic quantum field theory, paving the way to relativistic quantum computing schemes. This is a step beyond the various proposed nonrelativistic implementations of continuous variable cluster states.

Additional Information

How to cite this article: Bruschi, D. E. et al. Towards universal quantum computation through relativistic motion. Sci. Rep. 6, 18349; doi: 10.1038/srep18349 (2016).