Abstract
Much information about the structure and dynamics of a network is encoded in the eigenvalues of its transition matrix. In this paper, we present a first study on the transition matrix of a family of weight driven networks, whose degree, strength and edge weight obey power-law distributions, as observed in diverse real networks. We analytically obtain all the eigenvalues, as well as their multiplicities. We then apply the obtained eigenvalues to derive a closed-form expression for the random target access time for biased random walks occurring on the studied weighted networks. Moreover, using the connection between the eigenvalues of the transition matrix of a network and its weighted spanning trees, we validate the obtained eigenvalues and their multiplicities. We show that the power-law weight distribution has a strong effect on the behavior of random walks.
Similar content being viewed by others
Introduction
As a standard tool, random walks on a network describes various dynamical processes in the network, such as search1,2 spreading3, diffusion4, to name a few. Due to its role as a fundamental mechanism characterizing diverse other processes, random walks on complex networks have attracted considerable attention in the past years5,6,7,8,9,10,11,12,13,14,15,16,17,18,19. The vast literature provided novel methods for computing mean first-passage time, steady-state distribution, as well as many other properties of random walks.
Since random walks are completely described by the transition matrix20, most interesting quantities and properties related to random walks are determined by the spectra (eigenvalues and eigenvectors) of the transition matrix. First of all, the mean first-passage time from one node to another can be represented through the eigenvalues and eigenvectors of the transition matrix20. Furthermore, the sum of reciprocals of one minus every eigenvalue, excluding the eigenvalue 1 itself, determines the random target access time21. Finally, the smallest eigenvalue, together with the second largest eigenvalue, provides an upper bound and a lower bound for the mixing time22. In addition to the properties of random walks, the spectra of the transition matrix for a network are also pertaining to structural aspects of the network, for example, spanning trees23,24 and effective resistance25, which can also be determined by the spectra of Laplacian matrix26. Thus, transition matrix is closely related to Laplacian matrix, with the latter being widely used in quantum walks27,28 and quantum algorithms29.
In view of the significance, the study of spectra for transition matrix has become a central issue30. In the past decade, there has been important progress in determining the eigenvalues for transition matrix of different networks or characterizing their properties. Examples include random graphs31,32, Sierpinski gasket33,34, Tower of Hanoi graph35, Cayley tree and extend T-fractal36, fractal37,38 and non-fractal39,40 scale-free networks. These works provided a deeper understanding on spectral characteristics of the transition matrix of different networks, as well as the effects of network topology on the spectral density and random-walk process. Extensive empirical research has unveiled that real networks are characterized by the heterogeneity41,42, not only in the aspect of degree distribution43 but also in the context of weight distribution44,45,46. Previous works about spectra of the transition matrix were limited to binary networks and the influence of inhomogeneous weight distribution on the spectral properties of transition matrix still remains unknown.
In this paper, we study analytically the eigenvalues for transition matrix of a class of weighted networks47, which exhibit some prominent properties that are observed in real-world systems44,45,46, such as the power-law distribution of node degree, strength and edge weight. Based on the particular construction of the networks, we find all the eigenvalues and their corresponding multiplicities. Using the obtained eigenvalues, we deduce an explicit expression for the random target access time, as well as its leading scaling, which is different from those previously obtained for binary heterogeneous networks, implying that the weight has an important impact on the random-walk behavior. Moreover, we determine the weighted counting of spanning trees in the studied networks using the eigenvalues, which is consistent with that derived by another technique, corroborating the validity of our computation for the eigenvalues.
Results
Construction and properties of weight driven scale-free weighted networks
The network family, parameterized by two positive integer m and δ, is constructed in an iterative manner47. Let  denote the network class after g (g ≥ 0) iterations. Then, the network family is built as follows. For g = 0,
denote the network class after g (g ≥ 0) iterations. Then, the network family is built as follows. For g = 0,  consists of an edge (link) with unit weight connecting two nodes (vertices). For g ≥ 1,
consists of an edge (link) with unit weight connecting two nodes (vertices). For g ≥ 1,  is obtained from
is obtained from  by performing the following operations. For each edge with weight w in
by performing the following operations. For each edge with weight w in  , we add mw new nodes for either end of the edge and connect each of the mw new nodes to the end by new edges of unit weight; then we increase weight w of the edge by mδw. Figure 1 illustrates the network generation process for a special case of m = 2 and δ = 1.
, we add mw new nodes for either end of the edge and connect each of the mw new nodes to the end by new edges of unit weight; then we increase weight w of the edge by mδw. Figure 1 illustrates the network generation process for a special case of m = 2 and δ = 1.
Let Ng, Eg, Qg denote, respectively, the total number of nodes, the total number of edges and the total weight of all edges in  . And let nv(g) and ne(g) denote, respectively, the number of nodes and the number of edges that are created at iteration g. Then, ne(g) = nv(g) holds for all g ≥ 1. By construction, for g ≥ 0, we have
. And let nv(g) and ne(g) denote, respectively, the number of nodes and the number of edges that are created at iteration g. Then, ne(g) = nv(g) holds for all g ≥ 1. By construction, for g ≥ 0, we have

which under the initial condition Q0 = 1 yields

Furthermore, it is easy to derive that for all g ≥ 1,

Thus,

and

For an edge e connecting two nodes i and j in  , which is born at iteration τ, we use we(g) or wij(g) to denote its weight. Then, we(g) = wij(g) = (δm + 1)g−τ. Let si(g) (resp. di(g)) be the strength (resp. degree) of node i in
, which is born at iteration τ, we use we(g) or wij(g) to denote its weight. Then, we(g) = wij(g) = (δm + 1)g−τ. Let si(g) (resp. di(g)) be the strength (resp. degree) of node i in  , which is added to the network at generation gi. It is easy to obtain
, which is added to the network at generation gi. It is easy to obtain

and

where Ωi is the set of neighbors of i in  .
.
The resultant networks display prominent properties as observed in real systems44,45,46, with their degree, strength and edge weight following power law distribution47.
Eigenvalues and multiplicities of transition matrix
After introducing the construction and properties of the weighted scale-free networks, in this section we study eigenvalues and their multiplicities of the transition matrix for the networks.
Recursive relation of eigenvalues
Let Wg be the generalized adjacency matrix (weight matrix) of  . The entries Wg(i, j) of Wg are defined as follows:
. The entries Wg(i, j) of Wg are defined as follows:  if nodes i and j are adjacent in
if nodes i and j are adjacent in  , or
, or  otherwise. Then, the transition matrix for biased random walks48,49 in
otherwise. Then, the transition matrix for biased random walks48,49 in  , denoted by Tg, is defined as
, denoted by Tg, is defined as  , where Sg is the diagonal strength matrix of
, where Sg is the diagonal strength matrix of  with its ith diagonal entry being the strength si(g) of node i. Thus, the (i, j)th element of Tg is
with its ith diagonal entry being the strength si(g) of node i. Thus, the (i, j)th element of Tg is  , which represents the local transition probability for a walker going from node i to node j.
, which represents the local transition probability for a walker going from node i to node j.
We now consider the eigenvalues and eigenvectors of Tg. Since Tg is asymmetric, we introduce the following real and symmetric matrix Pg defined as

By definition, the (i, j)th entry of Pg is  . Since Pg is similar to Tg, they have the same set of eigenvalues. Furthermore, if ϕ is an eigenvector of matrix Pg associated with eigenvalue λ, then
. Since Pg is similar to Tg, they have the same set of eigenvalues. Furthermore, if ϕ is an eigenvector of matrix Pg associated with eigenvalue λ, then  is an eigenvector of Tg corresponding to eigenvalue λ. Therefore, we reduce the problem of finding eigenvalues for an asymmetric matrix Tg to the issue of determining eigenvalues for a symmetric matrix Pg.
is an eigenvector of Tg corresponding to eigenvalue λ. Therefore, we reduce the problem of finding eigenvalues for an asymmetric matrix Tg to the issue of determining eigenvalues for a symmetric matrix Pg.
Suppose that λ is an eigenvalue of Pg and  is its corresponding eigenvector, where ϕj is the component corresponding to node j in
is its corresponding eigenvector, where ϕj is the component corresponding to node j in  . Let
. Let  be a vector of dimension Ng−1 that is obtained from ϕ by restricting its components to the old nodes, namely, nodes generated before or at iteration g − 1. As will be shown below,
be a vector of dimension Ng−1 that is obtained from ϕ by restricting its components to the old nodes, namely, nodes generated before or at iteration g − 1. As will be shown below,  is an eigenvector of Pg−1, associated with eigenvalue
is an eigenvector of Pg−1, associated with eigenvalue  , from which λ is generated. By definition, we have
, from which λ is generated. By definition, we have

Let o be an old node in  . According to Eq. (9),
. According to Eq. (9),

where Θ denotes the set of the do(g) neighbors of node o. Let  be the set of the do(g − 1) old neighbors of node o, while the other new neighbors form set
be the set of the do(g − 1) old neighbors of node o, while the other new neighbors form set  . For each new neighboring node
. For each new neighboring node  , one has
, one has  , which implies
, which implies  . Thereby, the component ϕi satisfies
. Thereby, the component ϕi satisfies

implying

In the case λ≠0, inserting Eq. (12) into Eq. (10) and considering the two relations  and
and  , we obtain
, we obtain

an equation only involving old nodes, which were already existing at iteration g − 1.
For λ≠0, Eq. (13) is true for an arbitrary node present at generation g − 1. Thus, we can compare Eq. (13) with the following corresponding equation for the old node o at iteration g − 1:

This indicates that  is an eigenvector of Pg−1, corresponding to eigenvalue
is an eigenvector of Pg−1, corresponding to eigenvalue  .
.
It is not difficult to see that the entry Pg−1(o, i) of generation g − 1 is  times its counterpart Pg(o, i) of generation g. Then, Eqs. (13) and (14) coincide, provided that
times its counterpart Pg(o, i) of generation g. Then, Eqs. (13) and (14) coincide, provided that

which relates λ to  . Solving the quadratic equation in the variable λ given by Eq. (15) yields
. Solving the quadratic equation in the variable λ given by Eq. (15) yields

which shows that each eigenvalue  of Pg−1 gives rise to two eigenvalues of Pg, λ+ and λ−.
of Pg−1 gives rise to two eigenvalues of Pg, λ+ and λ−.
Let ϕ+ and ϕ− denote the eigenvectors of λ+ and λ−, respectively. Then, both ϕ+ and ϕ− can be obtained from  in the following way. For the nodes already present at iteration g − 1, the components of ϕ+ and ϕ− are equivalent to the corresponding components of
in the following way. For the nodes already present at iteration g − 1, the components of ϕ+ and ϕ− are equivalent to the corresponding components of  ; while for the nodes generated at iteration g, their components can be determined by replacing λ in Eq. (12) with λ+ or λ−. Therefore, λ+ (or λ−) has the same number of linearly independent eigenvectors as that of
; while for the nodes generated at iteration g, their components can be determined by replacing λ in Eq. (12) with λ+ or λ−. Therefore, λ+ (or λ−) has the same number of linearly independent eigenvectors as that of  . Moreover, the eigenvectors of λ+ (or λ−) are linearly independent, because Pg is real and symmetric.
. Moreover, the eigenvectors of λ+ (or λ−) are linearly independent, because Pg is real and symmetric.
Multiplicities of eigenvalues
Equation (16) indicates that from the eigenvalues of generation g − 1, one can obtain the eigenvalues of the next generation g, with the exception of those zero eigenvalues. Thus, if there exists an eigenvalue λ that cannot be derived from Eq. (16), it must be zero eigenvalue. Let  represent the degeneracy of eigenvalue λ for matrix Pg. Because Pg−1 is a real and symmetrical matrix, each eigenvalue
represent the degeneracy of eigenvalue λ for matrix Pg. Because Pg−1 is a real and symmetrical matrix, each eigenvalue  of Pg−1 has
of Pg−1 has  linearly independent eigenvectors. It is the same with either of its child eigenvalues, λ+ or λ−. Next we determine the multiplicity of each eigenvalue for matrix Pg.
linearly independent eigenvectors. It is the same with either of its child eigenvalues, λ+ or λ−. Next we determine the multiplicity of each eigenvalue for matrix Pg.
For small networks, the eigenvalues and their multiplicities can be calculated directly. The eigenvalues of P0 are 1 and −1. For P1, its eigenvalues are 1, −1, 0,  and
and  , where two pairs of eigenvalues (1 and
, where two pairs of eigenvalues (1 and  , −1 and
, −1 and  ) are generated, respectively, by eigenvalues 1 and −1 of P0. Moreover, the offspring eigenvalue of 1 and −1 has a single degeneracy. For g ≥ 2, the eigenvalues of matrix Pg display the following remarkable nature. Every eigenvalue appearing at current generation gi always exists at the next generation gi + 1 and all new eigenvalues of
) are generated, respectively, by eigenvalues 1 and −1 of P0. Moreover, the offspring eigenvalue of 1 and −1 has a single degeneracy. For g ≥ 2, the eigenvalues of matrix Pg display the following remarkable nature. Every eigenvalue appearing at current generation gi always exists at the next generation gi + 1 and all new eigenvalues of  are those produced via Eq. (16) by substituting
are those produced via Eq. (16) by substituting  with those eigenvalues that were newly borne at generation gi; moreover every new eigenvalue inherits the multiplicity of its parent. Hence, for g ≥ 2, all eigenvalues (excluding zero eigenvalue) of Pg are generated from 1, −1 and 0, with all the offspring eigenvalues of 1 and −1 being nondegenerate. Therefore, all that is left is to determine the multiplicity of 0, as well as the multiplicities of its descendants.
with those eigenvalues that were newly borne at generation gi; moreover every new eigenvalue inherits the multiplicity of its parent. Hence, for g ≥ 2, all eigenvalues (excluding zero eigenvalue) of Pg are generated from 1, −1 and 0, with all the offspring eigenvalues of 1 and −1 being nondegenerate. Therefore, all that is left is to determine the multiplicity of 0, as well as the multiplicities of its descendants.
Let r(M) denote the rank of matrix M. Then, the multiplicity of the zero eigenvalues for Pg is

We now evaluate r(Pg). For the set of all nodes in  , let α denote the subset of nodes in
, let α denote the subset of nodes in  and β the subset of nodes newly produced at generation g. Then, Pg can be written in a block form
and β the subset of nodes newly produced at generation g. Then, Pg can be written in a block form

where the fact that Pβ,β is the (Ng − Ng−1) × (Ng − Ng−1) zero matrix is used.
Notice that r(Pα,β) = r(Pβ,α). We can prove that (see Methods) Pβ,α is a full column rank matrix. Then,  and
and  . According to Eq. (17), the multiplicity of eigenvalue 0 for matrix Pg is:
. According to Eq. (17), the multiplicity of eigenvalue 0 for matrix Pg is:  for g = 0; and
for g = 0; and  for g ≥ 1. Because each eigenvalue in Pg keeps the degeneracy of its parent, the number of each of the first-generation descendants of zero eigenvalue is
for g ≥ 1. Because each eigenvalue in Pg keeps the degeneracy of its parent, the number of each of the first-generation descendants of zero eigenvalue is  , the number of each of the second-generation descendants of zero eigenvalue is
, the number of each of the second-generation descendants of zero eigenvalue is  and so on. Thus, the total number of zero eigenvalue and its descendants in Pg (g ≥ 1) is
and so on. Thus, the total number of zero eigenvalue and its descendants in Pg (g ≥ 1) is

For eigenvalue 1 (or −1), the total number of its descendants in Pg (g ≥ 0), including 1 (or −1) itself, is

Adding up the number of the above-obtained eigenvalues yields

which implies that we have found all the eigenvalues of matrix Pg and thus the transition matrix Tg.
Since the distribution of eigenvalues conveys much important information, in Fig. 2 we display as a histogram the distribution of eigenvalues for a specific network  for the case m = 2 and δ = 1. Because eigenvalues 1, −1 and their offspring are nondegenerate, we only provide the density of eigenvalue 0 and its descendants. Figure 2 indicates that the eigenvalue distribution is heterogeneous.
for the case m = 2 and δ = 1. Because eigenvalues 1, −1 and their offspring are nondegenerate, we only provide the density of eigenvalue 0 and its descendants. Figure 2 indicates that the eigenvalue distribution is heterogeneous.
Application of eigenvalues
In this section, we apply the obtained eigenvalues and their multiplicities to determine the random target access time for biased random walks and the weighted counting of spanning trees in the weighed scale-free networks  . Note that since
. Note that since  has a treelike structure, the weighted counting of spanning trees is just be the product of weights of all edges in
has a treelike structure, the weighted counting of spanning trees is just be the product of weights of all edges in  . Thus, our aim for evaluating this quantity is to verify that our computation for eigenvalues and their multiplicities is correct.
. Thus, our aim for evaluating this quantity is to verify that our computation for eigenvalues and their multiplicities is correct.
Random target access time
Transition matrix Tg describes the biased discrete-time random walks in  and thus various interesting quantities related to random walks are reflected in eigenvalues of the transition matrix. For example, the sum of reciprocals of 1 minus each eigenvalue (excluding eigenvalue 1 itself) of transition matrix Tg determines the random target access time, also called eigentime identity, in
and thus various interesting quantities related to random walks are reflected in eigenvalues of the transition matrix. For example, the sum of reciprocals of 1 minus each eigenvalue (excluding eigenvalue 1 itself) of transition matrix Tg determines the random target access time, also called eigentime identity, in  21.
21.
Let Hij(g) denote the mean first-passage time from node i to node j in  , defined as the expected time for a walker starting from node i to visit node j for the first time. Let
, defined as the expected time for a walker starting from node i to visit node j for the first time. Let  represent the steady state distribution for random walks on
represent the steady state distribution for random walks on  48,49, where
48,49, where  satisfying
satisfying  and
and  . The random target access time, denoted by
. The random target access time, denoted by  , for random walks on
, for random walks on  , is defined as the expected time needed by a walker from a node i to another target node j, chosen randomly from all nodes according to the steady state distribution, that is,
, is defined as the expected time needed by a walker from a node i to another target node j, chosen randomly from all nodes according to the steady state distribution, that is,

which does not depend on the starting node20 and can be recast as

Since  can be looked upon as the average trapping time of a special trapping problem11, it encodes much useful information about trapping in
can be looked upon as the average trapping time of a special trapping problem11, it encodes much useful information about trapping in  .
.
We introduce a matrix Lg = Ig − Pg, where Ig denotes the Ng × Ng identity matrix. Actually, Lg is the normalized Laplacian matrix23,25,31 of  . Let λi(g) (1 ≤ i ≤ Ng) be the Ng eigenvalues of Pg. By definition, for any i, σi(g) = 1 − λi(g) is an eigenvalue of Lg. It can be proved48 that
. Let λi(g) (1 ≤ i ≤ Ng) be the Ng eigenvalues of Pg. By definition, for any i, σi(g) = 1 − λi(g) is an eigenvalue of Lg. It can be proved48 that  can be represented in terms of the nonzero eigenvalues of Lg, given by
can be represented in terms of the nonzero eigenvalues of Lg, given by

where  is assumed, with λ1(g) = 1 being the largest non-degenerated eigenvalue of Pg.
is assumed, with λ1(g) = 1 being the largest non-degenerated eigenvalue of Pg.
In Methods, we derive that  obeys the following recursive relation:
obeys the following recursive relation:

which, with the initial condition  , is solved to obtain
, is solved to obtain

 can be further represented in terms of of network size Ng as
can be further represented in terms of of network size Ng as

Thus, for large networks (i.e.,  ),
),  , growing linearly with the network size. This is in sharp contrast to that obtained for unweighted scale-free treelike networks39 and Cayley tree36 (where
, growing linearly with the network size. This is in sharp contrast to that obtained for unweighted scale-free treelike networks39 and Cayley tree36 (where  ), as well as fractal trees (where
), as well as fractal trees (where  with η > 1)37,36. Thus, the heterogenous distribution of edge weight has a substantial influence on the behavior of random walks in weighted networks.
with η > 1)37,36. Thus, the heterogenous distribution of edge weight has a substantial influence on the behavior of random walks in weighted networks.
Weighted counting of spanning trees
For a weighted network  , denote by
, denote by  the set of its spanning trees. For a tree
the set of its spanning trees. For a tree  , its weight
, its weight  is defined to be the product of weights of all edges e in
is defined to be the product of weights of all edges e in  , that is,
, that is,  , where we is the weight of edge e. Let
, where we is the weight of edge e. Let  denote the weighted counting of spanning trees of
denote the weighted counting of spanning trees of  , which is defined by
, which is defined by  .
.
Since  is a tree, it has only one spanning tree, which is in fact
is a tree, it has only one spanning tree, which is in fact  itself. Then, the weighted counting of spanning trees in
itself. Then, the weighted counting of spanning trees in  is
is  , where the product is running over the weight we(g) of all edges
, where the product is running over the weight we(g) of all edges  . According to previous results24, we have
. According to previous results24, we have

For the sum term in the denominator of Eq. (28), we have

For the two product terms  and
and  in the numerator of Eq. (28), we use Δg and Λg to represent them, respectively. According to the above-obtained results, the two quantities Δg and Λg obey the following two recursive relations:
in the numerator of Eq. (28), we use Δg and Λg to represent them, respectively. According to the above-obtained results, the two quantities Δg and Λg obey the following two recursive relations:

and

Multiplying Eq. (30) by Eq. (31) results in

Applying Δ0 = 1 and Λ0 = 2, Eqs. (32) is solved to give

Inserting the results in Eqs. (29) and (33) into Eq. (28) yields

On the other hand, since  has a treelike structure,
has a treelike structure,  equals the product of weight of all edges in
equals the product of weight of all edges in  . Thus,
. Thus,  can be directly obtained by evaluating this product. By construction,
can be directly obtained by evaluating this product. By construction,  obeys the recursive relation
obeys the recursive relation  . Considering
. Considering  , we have
, we have  , which is consistent with Eq. (34), indicating the validity of our computation on the eigenvalues and their multiplicities for the transition matrix Tg of
, which is consistent with Eq. (34), indicating the validity of our computation on the eigenvalues and their multiplicities for the transition matrix Tg of  .
.
Discussion
In conclusion, we have considered the spectra of transition matrix for a class of weight-driven networks, whose degree, strength and edge weight follow power-law distribution, which is observed in various real-world systems. We have determined all the eigenvalues and their multiplicities of the transition matrix for the networks. Moreover, we have used the obtained eigenvalues to derive a closed-form expression about the random target access time for biased random walks taking place on the networks. Finally, we confirmed our results for the eigenvalues and their multiplicities via enumerating the weighted spanning trees, based on the connection between the two quantities.
We note that although the considered networks look self-similar, they are not topologically fractal. Since many real-life networks are fractal50,51,52, in future it deserves to study the spectra of transition matrix for weighted fractal networks. Furthermore, various structural and dynamical properties of a network are also relevant to the spectra of other matrices30, such as adjacency matrix and non-backtracking matrix. Future work should include determining the spectra for adjacency matrix31 and non-backtracking matrix53,54 of weighted scale-free networks.
Methods
Proof for the statement that P β,α is a full column rank matrix
Let v be an arbitrary vector of order Ng − Ng−1:

where Mi is the ith column vector of Pβ,α so that  . Let
. Let  . Assume that v = 0. Then, we can prove that ki = 0 holds for arbitrary ki. By construction, for any old node
. Assume that v = 0. Then, we can prove that ki = 0 holds for arbitrary ki. By construction, for any old node  , it has a new leaf neighboring node
, it has a new leaf neighboring node  . Then, in the expression
. Then, in the expression  , only
, only  , while all Mx,l = 0 for x≠i. From vl = 0, one obtains ki = 0. Hence, Pβ,α is a full column rank matrix.
, while all Mx,l = 0 for x≠i. From vl = 0, one obtains ki = 0. Hence, Pβ,α is a full column rank matrix.
Derivation for the recursive relation between  and
and 
Let 
 be the set of the Ng − 1 nonzero eigenvalues of matrix Lg. For g ≥ 1, Ωg includes 1, 2,
be the set of the Ng − 1 nonzero eigenvalues of matrix Lg. For g ≥ 1, Ωg includes 1, 2,  and other eigenvalues generated by them. Thus, Ωg can be classified into three nonoverlapping subsets
and other eigenvalues generated by them. Thus, Ωg can be classified into three nonoverlapping subsets  ,
,  and
and  , satisfying
, satisfying  , where
, where  consists of all the
consists of all the  eigenvalues 1,
eigenvalues 1,  contains only the unique eigenvalue
contains only the unique eigenvalue  and
and  includes those eigenvalues generated by 1, 2, or
includes those eigenvalues generated by 1, 2, or  . For
. For  and
and  , we have
, we have  and
and  . While for
. While for  , it can be evaluated in the following way.
, it can be evaluated in the following way.
From Eq. (15), we can derive the following relation dominating the eigenvalues of Lg and Lg−1:

which shows that every eigenvalue  in Ωg−1 generates two eigenvalues,
in Ωg−1 generates two eigenvalues,  and
and  , belonging to
, belonging to  . Using Vieta’s formulas, we obtain
. Using Vieta’s formulas, we obtain  and
and  . Then
. Then

which implies that

Combining the above-obtained results leads to the following recursive relation between  and
and  :
:

Additional Information
How to cite this article: Zhang, Z. et al. Spectra of weighted scale-free networks. Sci. Rep. 5, 17469; doi: 10.1038/srep17469 (2015).
References
Guimerà, R., Diaz-Guilera, A., Vega-Redondo, F., Cabrales, A. & Arenas, A. Optimal network topologies for local search with congestion. Phys. Rev. Lett. 89, 248701 (2002).
Bénichou, O., Loverdo, C., Moreau, M. & Voituriez, R. Intermittent search strategies. Rev. Mod. Phys. 83, 81–129 (2011).
Rosvall, M., Esquivel, A. V., Lancichinetti, A., West, J. D. & Lambiotte, R. Memory in network flows and its effects on spreading dynamics and community detection. Nat. Commun. 5, 4630 (2014).
Scholtes, I. et al. Causality-driven slow-down and speed-up of diffusion in non-Markovian temporal networks. Nat. Commun. 5, 5024 (2014).
Jasch, F. & Blumen, A. Target problem on small-world networks. Phys. Rev. E 63, 041108 (2001).
Kozak, J. J. & Balakrishnan, V. Analytic expression for the mean time to absorption for a random walker on the Sierpinski gasket. Phys. Rev. E 65, 021105 (2002).
Noh, J. D. & Rieger, H. Random walks on complex networks. Phys. Rev. Lett. 92, 118701 (2004).
Condamin, S., Bénichou, O. & Moreau, M. First-passage times for random walks in bounded domains. Phys. Rev. Lett. 95, 260601 (2005).
Bollt, E. M. & ben-Avraham, D. What is special about diffusion on scale-free nets? New J. Phys. 7, 26 (2005).
Condamin, S., Bénichou, O., Tejedor, V., Voituriez, R. & Klafter, J. First-passage times in complex scale-invariant media. Nature 450, 77–80 (2007).
Tejedor, V., Bénichou, O. & Voituriez, R. Global mean first-passage times of random walks on complex networks. Phys. Rev. E 80, 065104 (2009).
Burda, Z., Duda, J., Luck, J. & Waclaw, B. Localization of the maximal entropy random walk. Phys. Rev. Lett. 102, 160602 (2009).
Zhang, Z. Z. et al. Determining global mean-first-passage time of random walks on Vicsek fractals using eigenvalues of Laplacian matrices. Phys. Rev. E 81, 031118 (2010).
Bentz, J. L., Turner, J. W. & Kozak, J. J. Analytic expression for the mean time to absorption for a random walker on the Sierpinski gasket. II. The eigenvalue spectrum. Phys. Rev. E 82, 011137 (2010).
Lin, Y., Julaiti, A. & Zhang, Z. Z. Mean first-passage time for random walks in general graphs with a deep trap. J. Chem. Phys. 137, 124104 (2012).
Lin, Y. & Zhang, Z. Mean first-passage time for maximal-entropy random walks in complex networks. Sci. Rep. 4, 5365 (2014).
Bénichou, O. & Voituriez, R. From first-passage times of random walks in confinement to geometry-controlled kinetic. Phys. Rep. 539, 225–284 (2014).
Perkins, T. J., Foxall, E., Glass, L. & Edwards, R. A scaling law for random walks on networks. Nat. Commun. 5, 5121 (2014).
Zhang, Z., Li, H. & Sheng, Y. Effects of reciprocity on random walks in weighted networks. Sci. Rep. 4, 7460 (2014).
Lovász, L. Vol. 2 of Combinatorics, Paul erdos is eighty (Janos Bolyai Mathematical Society, Budapest, 1993).
Levene, M. & Loizou, G. Kemeny’s constant and the random surfer. Am. Math. Mon. 109, 741–745 (2002).
Sinclair, A. Improved bounds for mixing rates of Markov chains and multicommodity flow. Combin. Probab. Comput. 1, 351–370 (1992).
Chung, F. R. Spectral Graph Theory (American Mathematical Society, Providence, RI, 1997).
Chang, X., Xu, H. & Yau, S.-T. Spanning trees and random walks on weighted graphs. Pacific J. Math. 273, 241–255 (2015).
Chen, H. & Zhang, F. Resistance distance and the normalized Laplacian spectrum. Discrete Appl. Math. 155, 654–661 (2007).
Wu, F.-Y. Theory of resistor networks: The two-point resistance. J. Phys. A: Math. Gen. 37, 6653 (2004).
Agliari, E., Blumen, A. & Mülken, O. Dynamics of continuous-time quantum walks in restricted geometries. J. Phys. A: Math. Theor. 41, 445301 (2008).
Mülken, O. & Blumen, A. Continuous-time quantum walks: Models for coherent transport on complex networks. Phys. Rep. 502, 37–87 (2011).
Agliari, E., Blumen, A. & Muelken, O. Quantum-walk approach to searching on fractal structures. Phys. Rev. A 82, 012305 (2010).
Van Mieghem, P. Graph Spectra for Complex Networks (Cambridge University Press, Cambridge, 2011).
Chung, F., Lu, L. & Vu, V. Spectra of random graphs with given expected degrees. Proc. Natl. Acad. Sci. USA 100, 6313–6318 (2003).
Dorogovtsev, S. N., Goltsev, A. V., Mendes, J. F. & Samukhin, A. N. Spectra of complex networks. Phys. Rev. E 68, 046109 (2003).
Bajorin, N. et al. Vibration modes of 3n-gaskets and other fractals. J. Phys. A: Math. Theor. 41, 015101 (2008).
Bajorin, N. et al. Vibration spectra of finitely ramified, symmetric fractals. Fractals 16, 243–258 (2008).
Wu, S. & Zhang, Z. Eigenvalue spectrum of transition matrix of dual Sierpinski gaskets and its applications. J. Phys. A: Math. Theor. 45, 345101 (2012).
Julaiti, A., Wu, B. & Zhang, Z. Eigenvalues of normalized Laplacian matrices of fractal trees and dendrimers: Analytical results and applications. J. Chem. Phys. 138, 204116 (2013).
Zhang, Z., Hu, Z., Sheng, Y. & Chen, G. Exact eigenvalue spectrum of a class of fractal scale-free networks. Europhys. Lett. 99, 10007 (2012).
Zhang, Z., Sheng, Y., Hu, Z. & Chen, G. Optimal and suboptimal networks for efficient navigation measured by mean-first passage time of random walks. Chaos 22, 043129 (2012).
Zhang, Z. Z., Guo, X. Y. & Lin, Y. Full eigenvalues of the Markov matrix for scale-free polymer networks. Phys. Rev. E 90, 022816 (2014).
Xie, P., Lin, Y. & Zhang, Z. Spectrum of walk matrix for koch network and its application. J. Chem. Phys. 142, 224106 (2015).
Boccaletti, S., Latora, V., Moreno, Y., Chavez, M. & Hwang, D.-U. Complex networks: Structure and dynamics. Phys. Rep. 424, 175–308 (2006).
Newman, M. E. J. Networks: An Introduction (Oxford University Press, Oxford, UK, 2010).
Barabási, A.-L. & Albert, R. Emergence of scaling in random networks. Science 286, 509–512 (1999).
Barrat, A., Barthelemy, M., Pastor-Satorras, R. & Vespignani, A. The architecture of complex weighted networks. Proc. Natl. Acad. Sci. USA 101, 3747–3752 (2004).
Barrat, A., Barthélemy, M. & Vespignani, A. Weighted evolving networks: Coupling topology and weight dynamics. Phys. Rev. Lett. 92, 228701 (2004).
Barrat, A., Barthélemy, M. & Vespignani, A. Modeling the evolution of weighted networks. Phys. Rev. E 70, 066149 (2004).
Zhang, Z. et al. Recursive weighted treelike networks. Eur. Phys. J. B. 59, 99–107 (2007).
Zhang, Z., Shan, T. & Chen, G. Random walks on weighted networks. Phys. Rev. E 87, 012112 (2013).
Lin, Y. & Zhang, Z. Random walks in weighted networks with a perfect trap: An application of Laplacian spectra. Phys. Rev. E 87, 062140 (2013).
Song, C., Havlin, S. & Makse, H. A. Self-similarity of complex networks. Nature 433, 392–395 (2005).
Song, C., Havlin, S. & Makse, H. A. Origins of fractality in the growth of complex networks. Nat. Phys. 2, 275–281 (2006).
Gallos, L. K., Song, C. & Makse, H. A. A review of fractality and self-similarity in complex networks. Physica A 386, 686–691 (2007).
Krzakala, F. et al. Spectral redemption in clustering sparse networks. Proc. Natl. Acad. Sci. USA 110, 20935–20940 (2013).
Morone, F. & Makse, H. A. Influence maximization in complex networks through optimal percolation. Nature (2015).
Acknowledgements
This work was supported by the National Natural Science Foundation of China under Grant No. 11275049. X.Y.G. was also supported by Fudan’s Undergraduate Research Opportunities Program.
Author information
Authors and Affiliations
Contributions
Z.Z. designed the research; X.G. and Y.Y. performed the research; Z.Z. and X.G. wrote the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Zhang, Z., Guo, X. & Yi, Y. Spectra of weighted scale-free networks. Sci Rep 5, 17469 (2015). https://doi.org/10.1038/srep17469
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep17469
This article is cited by
-
Quantization Effects on Complex Networks
Scientific Reports (2016)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

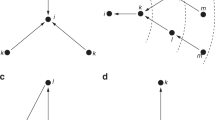


 corresponding to m = 2 and δ = 1.
corresponding to m = 2 and δ = 1. and
and 