Abstract
Existing computational tools for de novo metabolic pathway assembly, either based on mixed integer linear programming techniques or graph-search applications, generally only find linear pathways connecting the source to the target metabolite. The overall stoichiometry of conversion along with alternate co-reactant (or co-product) combinations is not part of the pathway design. Therefore, global carbon and energy efficiency is in essence fixed with no opportunities to identify more efficient routes for recycling carbon flux closer to the thermodynamic limit. Here, we introduce a two-stage computational procedure that both identifies the optimum overall stoichiometry (i.e., optStoic) and selects for (non-)native reactions (i.e., minRxn/minFlux) that maximize carbon, energy or price efficiency while satisfying thermodynamic feasibility requirements. Implementation for recent pathway design studies identified non-intuitive designs with improved efficiencies. Specifically, multiple alternatives for non-oxidative glycolysis are generated and non-intuitive ways of co-utilizing carbon dioxide with methanol are revealed for the production of C2+ metabolites with higher carbon efficiency.
Similar content being viewed by others
Introduction
Microbial metabolism describes the full range of enzymatic conversions of carbon substrates to cellular biomass precursors, energy equivalents and biochemical molecules. Metabolic engineering harnesses this metabolic machinery for converting feedstock substrates to a growing range of products1,2,3. Starting with single gene mutations, the range of interventions over the past decade has expanded considerably to enable genome-wide editing and pathway assembly4. The use of system and synthetic biology tools have enabled the tunable regulation of genes5,6,7,8, assembly of heterologous pathways9,10 and temporal control of gene expression11,12. Recent advances in multiplex engineering (e.g., MAGE13), efficient genome-editing (e.g., CRISPR-Cas14,15) and genome-wide regulation of gene expression through small RNAs16 have brought closer the dream of “designer cells” that can catalyze any tailor-made stoichiometry-balanced metabolic conversion with high specificity and control17. Concurrent with experimental efforts, computational strain design tools relying on stoichiometry18,19,20 along with kinetic expressions21,22 is increasingly being used to guide the redesign of microbial metabolism. So far, these redesign approaches have mostly concentrated on retrofitting the metabolic capabilities of the production host by preventing carbon loss and ensuring proper redox supply.
Existing computational procedures for the de novo pathway design rely on either optimization techniques or graph-search approaches. Linear Programming (LP) and Mixed Integer Linear Programming (MILP) approaches for pathway design, in general, extract a minimal stoichiometry-balanced sub-network that converts a source metabolite to a target chemical with high yield23. While early work was restricted to design pathways for small-to-medium size networks24,25,26, recent procedures have reached up to genome-scale size27,28,29 often using the concept of elementary modes30 and comprehensive databases of reactions31,32,33,34. However, these procedures do not necessarily conform to a previously identified optimal conversion stoichiometry thereby missing the opportunity to optimally recycle intermediates to reach a maximum yield.
Graph-based pathway design approaches35 begin from the target chemical and iteratively retrace back a path to the source metabolite using a retrosynthetic algorithm. Using a depth-first search, variations of the k-shortest path approach have been used to design and classify pathways based on their length36, negativity of free energy change for each reaction step37, or use of intermediate metabolites with the fewest connections38. Graph-search approaches can be supplemented with “reaction-rules” that can suggest de novo reaction steps between any two metabolites often absent in existing databases (e.g., BNICE39, Pertusi et al.40, GEM-Path41). In most cases, the consumption (or production) of cofactors and possibly co-reactants or co-products required for these pathways to operate is not directly tracked42. As a result, these procedures are often coupled with a post-processing step where a Flux Balance Analysis (FBA) is performed to select pathways that are stoichiometry-balanced and maximize the production of target chemicals. As with LP or MILP based approaches, generally mostly linear pathway topologies are traced.
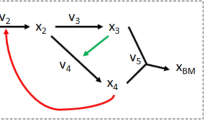
Powerful as these approaches have been, their primary shortcoming lies in the fact that they aim to trace pathways connecting a single substrate (A) to a single product (B). However, metabolic conversions do not generally involve linear paths from substrate to product43. Most metabolic engineering tasks recruit many more metabolites and reactions than the ones along the main carbon conversion path. Cofactor usage, co-reactant choices as well as stoichiometric ratios are important decision variables during the pathway design stage. It is the overall stoichiometry that globally captures the overall goal rather than just the origin and destination molecules. The term overall stoichiometry/conversion abstracts the global elemental balance sheet for the chemical changes including metabolites, small molecules, ions and free energy equivalents required to achieve the design objective. Meeting this overall stoichiometry often requires the recruitment of many additional metabolites that help recycle carbon and redox resources in highly complex ways. This motivates the development of a stoichiometry and pathway design tool (Fig. 1) that first optimizes the overall stoichiometry (e.g., aA + cC → bB + dD) by exploring exhaustively co-reactant/co-product combinations (Step 1). The coefficients in the overall stoichiometry (i.e., a, b, c and d) are critical as they ultimately define the carbon and energy efficiency of the conversion while meeting thermodynamic feasibility. Following the selection of the overall reaction (i.e., optStoic, see Fig. 1 and Methods), intervening reactions can be identified from a database (Step 2) that links the chosen reactants and products in the desired stoichiometric ratios (i.e., minRxn/minFlux, see Fig. 1 and Methods).
Pictorial representation of the two-step (optStoic + minRxn/minFlux) overall stoichiometry and reaction network design procedure.
Step 1 (optStoic) identifies the overall stoichiometry of conversion from (A to B) maximizing a desired performance objective subject to overall constraints of elemental and charge balance and thermodynamic feasibility. Additional unknown co-reactant/co-product combinations (C, D) from a metabolite database and their respective stoichiometric coefficients in the overall conversion (b, c, d) are determined at this stage (in red). Step 2 identifies a network of reactions (in red) from a reaction database that meet the overall stoichiometry from Step 1 by either minimizing the number of reactions (minRxn) or the total metabolic flux (minFlux), subject to constraints of stoichiometric balance and reaction directionality. Additional constraints exploring alternate overall reaction stoichiometry (in Step 1) and network designs (in Step 2) are shown in grey.
We demonstrate the two-step procedure for three separate case studies of increasing complexity. The first one exhaustively identifies networks that convert glucose to acetate while conserving all carbon atoms with no provision for any additional co-reactants or co-products in the spirit of the recent study by Bogorad et al.44. The second study explores the reverse problem of identifying new ways of forming carbon-carbon bonds from the combined use of methanol and CO2 to stoichiometry-feasible C2+ products. Finally, the third study identifies suitable co-reactant and co-product pairs to drive forward the thermodynamically unfavorable methane to acetate conversion. The two-stage procedure recapitulates existing pathway designs45,46,47,48 and identifies novel pathway topologies inaccessible to existing algorithms. Overall conversion stoichiometries and pathway designs span a range of complex network topologies and provide valuable insight as to how the overall conversion pathway changes in response to alternate co-reactant and/or co-product scenarios.
Results
Brief description of the proposed two-step workflow
The first step (optStoic) identifies the stoichiometric coefficients of the reactant and product metabolites in the overall conversion while maintaining thermodynamic feasibility considerations (Fig. 1). At this stage, not just the overall conversion stoichiometry but also some of the co-reactants and/or co-products are yet to be determined. Generally, the goal during this scoping phase is to identify an overall conversion that maximally utilizes a limiting carbon resource towards a target product while the intervening reaction steps are left at this stage unexplored. Ancillary considerations may include (i) co-utilization of other carbon substrates (e.g., gaseous reactants), (ii) possible co-production of valuable by-products, (iii) budgeting for a minimum level of biomass and growth or non-growth associated ATP, etc. Both the identity of some of the reactants and products as well as the overall stoichiometry are degrees of freedom that can be optimized towards meeting the above stated performance objectives. In addition to constraints on elemental and charge balances on the overall conversion respectively, a thermodynamic feasibility constraint is imposed to ensure that the free energy change of the overall conversion is below a pre-set negative threshold. Economic considerations implied by the prices of reactant and product molecules can also be imposed directly. The optStoic optimization formulation (see Methods for details) yields an LP model.
The second step searches through a database of elementally and charge balanced reactions (accessed from MetRxn49) to extract a (generally minimal) set of reactions that conform to the overall conversion stoichiometry identified under the first step (Fig. 1). Exchange reactions for only the metabolites present in the overall stoichiometry are added to allow for their uptake and export, respectively and their exchange fluxes are fixed according to the overall stoichiometry determined by optStoic. Consequently, all flux from the reactant metabolites is routed directly or recycled through intermediates towards the target metabolites. The optimization problem could either minimize the total number of active reactions in the design (minRxn) or, alternately minimize the sum of non-zero fluxes (minFlux) to approximate the enzyme load required to achieve the overall conversion. Requirements on negativity of the free energy change of each individual reaction step, as well as number of heterologous reactions in the pathway can also be imposed to help rank-order all identified designs. minRxn yields an MILP optimization formulation whereas minFlux a much more tractable LP representation.
The two-stage stoichiometry and intervening reaction design procedure (optStoic + minRxn/minFlux) was implemented for three case studies that highlight the potential of the approach in identifying novel stoichiometries and network designs.
Case Study 1: Synthetic pathways for fully converting glucose to acetate
Conversion of glucose through central carbon metabolism to acetyl-CoA (through EMP glycolysis or Entner-Doudoroff pathway) is required by most microorganisms for the production of biomass precursors and cofactors50. These pathways are also often recruited for the production of various bioproducts in a variety of production hosts. The generation of ATP and redox equivalent for growth, however, comes at the expense of losing two carbon atoms per glucose molecule as carbon dioxide reducing carbon yield to a maximum of 67%. Alternate modes of glucose metabolism, such as the glycerate pathway51 lead to the same carbon loss. An exception to this rule is found in some clostridial52 and lactate-producing bacteria53 that use a phosphoketolase enzyme to process glucose without any carbon loss to CO2. Recently, a synthetic, non-oxidative glycolysis (NOG) cycle was designed and assembled demonstrating the feasibility of this concept44 for bioconversion. By expressing in E. coli heterologous phosphoketolase enzymes xylulose-5-phosphate phosphoketolase (XPK) and fructose-6-phosphate phosphoketolase (FPK) from B. adolescentis Bogorad et al.44 assembled three cyclic networks demonstrating complete conversion of glucose to acetate. In this case study, we benchmark the proposed computational method for the same conversion and explore additional network designs beyond the ones described in Bogorad et al.44.
The first step (i.e., optStoic, see Methods) here is redundant as the overall stoichiometry in the form of A → 3B is fixed. Only networks that conserve all carbon flux from glucose to acetate satisfy the imposed overall stoichiometry. Results from both minRxn and minFlux (see Methods) converged to the same designs that achieve the overall conversion albeit with substantial differences in computational time. The smallest network (Fig. 2a) recapitulated the engineered construction of Bogorad et al.44 where glucose undergoes a stepwise conversion to acetyl phosphate (actp) in a cyclic route. A number of alternate routes using FPK or XPK as the sole deacetylating reaction were identified similar to those constructed in Bogorad et al.44 (see Fig. 2b for one of the constructions). Note that in this network design the need for cofactors NADH and NAD is balanced with a zero net requirement. minRxn/minFlux can also be used to directly limit the number of reactions with a positive standard change in free energy. While both NOG and all designs shown in Fig. 2a,b require at least one reaction with a positive standard free energy change (i.e., ribulose-5-phosphate isomerase (RPI)), the design depicted in Fig. 2c involves no reaction with positive ΔG0 (see Methods) whereby the thermodynamically unfavorable conversion of ribose-5-phosphate (r5p) to ribulose-5-phosphate (ru5p) is avoided by routing Pentose Phosphate Flux through C5 metabolism of phosphoribosyl pyrophosphate (prpp) and ribulose (rub) in E. coli (see Supplementary Text S1 for details). However, as a trade-off this cycle consumes one additional ATP compared to other designs. Networks not involving any phosphoketolase enzymes can also be designed (Fig. 2d) where glucose uses the modified RuMP pathway to produce three molecules of ethylene glycol. Diol dehydratase (DDT54) removes a water molecule from ethylene glycol to synthesize acetaldehyde (acald), which can be oxidized to acetate in three steps. This route can be potentially advantageous for the co-utilization of five and six carbon substrates55.
Six alternate network designs for conversion of glucose to acetate with 100% carbon efficiency.
The full description of the abbreviated reaction (in upper case) and metabolite (in lower case) names is listed in Supplementary Data Files S3 and S4, respectively. The molar flux values for each reaction are shown in italics under the reaction names.
We next explored whether it is possible to construct the entire pathway in a single organism (see Methods) unlike the engineered NOG pathway that requires at least one heterologous enzyme (i.e., either FPK or XPK). Figure 2e illustrates one such design with reactions from only clostridial species such as C. ljungdahlii56 or thermophilic organisms such as Moorella thermoacetica57 (see Supplementary Data File S5). Here, the EMP pathway is combined with the Wood-Ljungdahl cycle to fix the CO2 lost in the conversion of pyruvate (pyr) to acetyl-CoA in pyr ferredoxin oxidoreductase enzyme (PFOR)58. Note that all network designs introduced here have a net zero ATP balance as specified in the overall stoichiometry. In contrast, the NOG pathway can produce two ATP molecules (per glucose molecule) from actp hydrolysis. By combining glycolysis and Wood-Ljungdahl we can in principle provide four ATP molecules (Fig. 2e). An alternate pathway (Fig. 2f) with a maximum generation of three ATP molecules can also be constructed using enzyme in the ED pathway. Here, the serine metabolism is utilized instead of the western branch of Wood-Ljungdahl cycle. However, practical hurdles in fixing all the CO2 released in pyruvate decarboxylation (PFOR) and glycine cleavage (GLYCL) may make these pathways difficult to engineer.
The trade-off in flux allocation between acetate production and cellular growth was assessed by including biomass formation (derived from the biomass equation in iAF1260 E. coli model59) as an additional product in the overall stoichiometry (see Methods). The study revealed that while maximum acetate production was limited by carbon availability at lower biomass levels, thermodynamic feasibility was the limiting factor at higher biomass levels due to increased demands for growth-associated maintenance ATP.
In this example, we examined how optimization formulations minRxn/minFlux can be used to select reactions that fully convert glucose to acetate while exploring the impact of minimizing reactions with a positive ΔG0, selection of production host and minimality of reactions in the designed conversion pathway.
Case study 2: Co-utilization of methanol and carbon dioxide to C2+ compounds
In the second case study, we focus on the design of the overall conversion when not all participating metabolites are known a priori (see Methods). Methanol is an important commodity chemical and petrochemical by-product60 industrially produced from syngas. However, limitations in direct industrial catalytic condensation of methanol61 have so far limited the direct utilization of this low energy density molecule towards biofuel products such as ethanol and other C2+ molecules. A recent study has addressed this limitation by proposing and constructing a biological route for the direct condensation of methanol to ethanol46 with 100% efficiency of carbon conversion. Here we explore novel designs that can simultaneously convert methanol and co-utilize CO2 towards C2+ product metabolites with zero loss of carbon flux (i.e., A + C → B reaction). Note that product metabolite B is treated as unknown and could potentially be any of the 3,330 C2+ metabolites in set I (list of metabolites). The negative free energy change for methanol condensation (ΔG = −16.25 kcal mol−1) allows for the endergonic uptake of some CO2 to become thermodynamically feasible. As a result, designed pathways have the potential to achieve higher carbon efficiency than existing methanol condensation routes46 while also exhaustively exploring all possible C2+ product metabolites.
We chose maximization of the coefficient of CO2 in the overall stoichiometry as the design objective in optStoic while keeping the methanol coefficient at a value of one. This objective function maximizes the carbon yield of the desired product per mole of the limiting reactant (methanol). As many as 496 target metabolites from set I were identified as thermodynamically feasible products for the conversion (see Supplementary Data File S1 for full list). Table 1 shows ten of the designs in decreasing order of CO2 uptake. CO2 uptake varies in concert with the oxygen to hydrogen ratio (O:H) in the product metabolite. For example, malonate (C3H4O4), which has an O:H ratio of one, has the largest stoichiometric coefficient for CO2 (i.e., 1.25), while 2-methyl butanal (O:H = 0.1) has the lowest (i.e., 0.0714). As hydrogen availability in the reactants is fixed (stoichiometry of methanol is fixed to one), a low O:H ratio in the product reduces water production to satisfy elemental hydrogen balance. Because the oxygen atoms in CO2 are routed to water for products with low O:H ratio, reduced water production limits caused by the fixed availability of H, reduces the co-utilization of CO2 and thus overall carbon yield. It is important to note that the O:H ratio is also critical in deciding whether a desired metabolite is a feasible target product. For example, several platform chemicals such as ethylene glycol (O:H = 0.33), 1-butanol (O:H = 0.1) and 1,3-propanediol (O:H = 0.25) are not feasible solutions as mass conservation of hydrogen and oxygen cannot be simultaneously satisfied in the overall stoichiometry. Furthermore, metabolites with a very high O:H ratio, such as oxalate (O:H = 2) and glyoxylate (O:H = 1.5) are also not feasible due to limitations in oxygen atoms availability from CO2. Therefore, constraints of the overall design stoichiometry determine the feasibility of the target products as well as their maximum yields. It appears that in all designs thermodynamic feasibility is not the limiting constraint, instead elemental balances for H and O limit overall reaction stoichiometries.
From Table 1, we selected four products (i.e., acetate, 3-hydroxybuyrate, 2-ketoisovalerate and phloroglucinol) for constructing networks satisfying their overall reaction stoichiometry (Figs 3 and 4). Both 3-hydroxybuyrate and 2-ketoisovalerate are platform chemicals62 that also serve as precursors to other biochemicals41,62 while phloroglucinol is a phenolic derivative used as a building block for cosmetics63 and explosives64. Note that for the construction of the networks we scaled up the overall stoichiometry such that all the coefficients are integers. Optimization formulations minRxn/minFlux revealed that the optimal reaction networks for each conversion involved a common core of reactions that initially convert the C1 substrates to an intermediate product (i.e., acetyl-CoA), which was subsequently routed towards the final product. As a result, the first example (acetate production) spans alternate routes of fixing CO2 with methanol to acetyl-CoA (and acetate). Each one of the identified networks is subsequently coupled with additional reactions to synthesize the three other target products (i.e., 3-hydroxybuyrate, 2-ketoisovalerate and phloroglucinol). The optimal network for converting methanol and CO2 to acetate is divided into two modules (Fig. 3a, Supplementary Text S1). The first module condenses four molecules of CO2 and methanol to synthesize four acetyl-CoA molecules using a combination of methylotropic and Wood-Ljungdahl pathway enzymes. The reducing equivalents (ferredoxin) required for powering this conversion is supplied by methanol oxidation in methanol dehydrogenase (MEDH) in the second module. This module assembles an alternative methanol condensation46 cycle where four formaldehyde molecules enter a modified ribulose monophosphate (RuMP) Pathway65 to condense to two actp molecules. Hexulose-6-phosphate synthase (HPS) and 6-phospho-3-hexulo isomerase (PHI) found in methylotrophs65 fix formd into the five-carbon ru5p backbone which is subsequently cleaved in FPK. Pentose Phosphate enzymes convert the intermediate substrates back to ru5p to complete the cycle using reactions also present in the NOG cycle.
Designs for the co-utilization of methanol and carbon dioxide towards (A) 3-hydroxybutyrate (B) 2-ketoisovalerate and (C) phloroglucinol. The biosynthetic network for acetyl-CoA (accoa) from methanol and carbon dioxide is shown in Figure 3. Metabolic pathways explored in previous studies are highlighted in blue, while proposed ones are highlighted in green. Existing pathway for phloroglucinol production with lower energy efficiency is highlighted in red.
The design shown in Fig. 3a requires the fewest number of reactions, however, the oxygen-sensitive nature of the Wood-Ljungdahl enzymes (MTA, ACS)46 could be a practical concern. The second synthetic design (Fig. 3b) uses histidine degradation metabolism66 and formate dehydrogenase (FDH) from clostridia67 to fix CO2 for acetate production. A third design using predominantly E. coli reactions (Supplementary Data File S5) was also identified (Fig. 3c). Here, half of the formaldehyde (from methanol) is fixed in the modified RuMP cycle and the rest is fixed along with CO2 in a functional reversal of the glyoxylate shunt68. As all the reactions in this design are either native to E. coli or have been successfully expressed in prior studies (malate thiokinase, malyl-CoA ligase)68, it has the fewest potential barriers for its implementation.
Each one of these cyclic routes can be combined with additional paths to route acetyl-CoA flux towards other target chemicals. Figure 4a–c show routes for converting methanol and CO2 to a C4, a C5 and a C6 product, respectively. Pathways for 3-hydroxybutyrate (3hbut) recapitulate existing engineered routes through acetoacetyl-CoA69,70 while also proposing additional synthetic designs that utilize succinate synthesis (through a modified TCA cycle) and metabolism (through β-oxidation reversal) routes (Fig. 4a). In addition to thiamine-dependent valine synthesis pathway for 2-ketoisovalerate (2kiv) production71, an alternate route linking β-oxidation reversal with valine degradation is also identified (Fig. 4b). In the case of phloroglucinol (phgl) production, however, the traditional pathway using malonyl-CoA metabolism72 was not identified by minFlux as the acetyl-CoA carboxylase (ACCOAC) step requires three additional ATP thus violating the overall energy balance fixed in optStoic (Fig. 4c in red). Instead, acetyl-CoA was converted to 3-hydroxybutyryl-CoA (3hbutcoa) which incorporates an additional acetyl-CoA molecule to form 3-hydroxy-5-oxohexanoyl-CoA (in 3-hydroxy-5-oxohexanoyl-CoA thiolase (3HXCT)). Cyclization and reduction of this molecule synthesizes phloroglucinol (Fig. 4c in green).
This case study highlights several of the advantages of the proposed procedure over existing pathway prospecting tools. Performance metrics can be directly imposed without the need for post-processing steps unlike existing procedures31,41,73. Constraints on overall stoichiometry filter out infeasible routes and unbalanced conversions. The designs are not restricted to linear paths36,41,74, but can explore cyclic routes connected not only by carbon transfer, but also through cofactor balances where the participating metabolites and their coefficients can be design variables.
Case Study 3: Designing thermodynamically feasible paths for the conversion of methane to acetate
In the previous case study, only co-product (B) was unknown in the overall conversion. In the third case study, both co-reactant (C) and co-product (D) are design variables. With increased production of methane from natural gas deposits through advanced extraction technologies75, there is a growing interest of engineering metabolic routes of fixing this gaseous feedstock to C2+ liquid biofuel and biochemical targets76. However, the overall conversion creating a C-C bond by fixing methane with a C1 co-substrate (e.g., atmospheric CO2, CO from syngas, etc.) is thermodynamically unfavorable (e.g., ΔG = 11.05 kcal for CH4 + CO2 → CH3COOH). Recent studies have suggested that such a conversion can be achieved when coupled with a suitable electron acceptor77,78. Several anaerobic microorganisms have evolved ways to couple oxidation of methane with reduction of electron acceptors such as nitrite, sulfate79, iron and manganese80. In this study, we first identify all electron acceptors that could be used to convert methane to acetate (C2 product) and rank them according to their carbon yield to acetate. Subsequently, we select five solutions from the list of feasible electron acceptors to design pathways that convert methane and a C1 co-substrate (CO2 or CO) to acetate along with a C2+ platform chemical1,81.
Using optStoic and keeping the stoichiometry of acetate fixed at one (as a basis), we maximized the stoichiometric coefficient of methane while allowing the production of up to two additional metabolites from set I. Non-carbon containing metabolites including metal ions, anions, protons and water were included as candidates in the overall stoichiometry. optStoic identified many distinct designs with alternative electron-acceptor combinations. Ten such designs are shown in Table 2 (see Supplementary Data File S2 for all the designs). Here, the overall reaction stoichiometry has been rescaled for unit molar consumption of the electron acceptor. The only feasible stoichiometry with a single additional co-metabolite was oxygen. We did not analyze further this stoichiometry as designs for aerobic conversion of methane have already been explored extensively76,82. Results demonstrate the varying capacity of different electron-accepting pairs in oxidizing methane to acetate due to thermodynamic considerations. The reduction of one mole of tetrathionate  to hydrogen sulfide (H2S) accepts the maximum number of electrons (eighteen) thus converting 4.5 moles of methane to 2.25 moles of acetate. In contrast, one mole of iron(III)/iron(II) reduction
to hydrogen sulfide (H2S) accepts the maximum number of electrons (eighteen) thus converting 4.5 moles of methane to 2.25 moles of acetate. In contrast, one mole of iron(III)/iron(II) reduction  oxidizes only 0.25 moles of methane as it accepts only one electron. The electron acceptor pair
oxidizes only 0.25 moles of methane as it accepts only one electron. The electron acceptor pair  also supplies the oxygen required for the carbonyl group in acetate and oxidize additional hydrogen in methane to water. Most of the electron accepting pairs such as nitrate/nitrite
also supplies the oxygen required for the carbonyl group in acetate and oxidize additional hydrogen in methane to water. Most of the electron accepting pairs such as nitrate/nitrite  and bisulfite/hydrogen sulfide
and bisulfite/hydrogen sulfide  can perform both tasks. However,
can perform both tasks. However,  pair only performs the role of electron acceptor while water supplies the oxygen. Note that the commonly found electron pair sulfate/hydrogen sulfide reduction
pair only performs the role of electron acceptor while water supplies the oxygen. Note that the commonly found electron pair sulfate/hydrogen sulfide reduction  utilized by several marine anaerobic consortia for methane oxidation83,84 was not identified as a feasible solution as ΔGoverall of the reaction (−4.41 kcal mol−1 acetate) was below the conservatively chosen ΔGmin(−5 kcal mole−1 acetate) for this case study.
utilized by several marine anaerobic consortia for methane oxidation83,84 was not identified as a feasible solution as ΔGoverall of the reaction (−4.41 kcal mol−1 acetate) was below the conservatively chosen ΔGmin(−5 kcal mole−1 acetate) for this case study.
For the second step we selected five pairs of electron acceptors from Table 2 (i.e.,  ,
,  ,
,  ,
,  and
and  ) with different efficiencies of methane fixation per mole of oxidizing metabolite. For a unit mole conversion of each pair, we searched for a stoichiometry that further improves methane uptake by allowing for up to two additional metabolites from set I (similar to Step 1). The co-substrates were restricted to CO2 and CO while the co-products were chosen from all C2+ compounds (3,330 in set I). Table 3 compares ten of the designs for
) with different efficiencies of methane fixation per mole of oxidizing metabolite. For a unit mole conversion of each pair, we searched for a stoichiometry that further improves methane uptake by allowing for up to two additional metabolites from set I (similar to Step 1). The co-substrates were restricted to CO2 and CO while the co-products were chosen from all C2+ compounds (3,330 in set I). Table 3 compares ten of the designs for  and
and  electron acceptors. Both acceptors exhibit the same general trend of higher methane utilization for products with a higher carbon ratio. In contrast to Case Study 2, it was the thermodynamic feasibility of the overall reaction and not the O:H ratio of the product that was limiting methane utilization. By allowing both the reactant and co-reactant stoichiometries to vary we have an additional degree to freedom to match the O:H ratio of the target product and maximize methane utilization all the way to the thermodynamic limit (i.e., ΔGoverall = −5 kcal). It is also interesting to note that
electron acceptors. Both acceptors exhibit the same general trend of higher methane utilization for products with a higher carbon ratio. In contrast to Case Study 2, it was the thermodynamic feasibility of the overall reaction and not the O:H ratio of the product that was limiting methane utilization. By allowing both the reactant and co-reactant stoichiometries to vary we have an additional degree to freedom to match the O:H ratio of the target product and maximize methane utilization all the way to the thermodynamic limit (i.e., ΔGoverall = −5 kcal). It is also interesting to note that  allows for much higher efficiency of methane fixation compared to
allows for much higher efficiency of methane fixation compared to  . This is also because the thermodynamic driving force and not the electron-accepting capability of the electron acceptor becomes the limiting factor in this case.
. This is also because the thermodynamic driving force and not the electron-accepting capability of the electron acceptor becomes the limiting factor in this case.
 and
and  for ten target products.
for ten target products.Each one of the five electron acceptors was used to suggest minimal networks for fixing methane to a different target product (see Figs 5 and 6). Similar to previous study, a core set of reactions first converted methane and the co-reactant to the intermediate acetyl-CoA. We chose the first alternative (i.e.,  ) to explore ways of co-utilizing methane and CO2 (or CO) towards acetate (Fig. 5). Additional designs provide pathways from acetate to the final products (Fig. 6). All designs show that the terminal acceptors exchanged electrons with a cofactor pair instead of directly catalyzing a reaction in the carbon-transfer network. Different cofactors were identified for the electron acceptors depending on the reduction reactions in the network (see Supplementary Text S1 for details). Note that a few of the designs require electron transfer between NADH/NADPH and ferredoxin for regeneration of reduced ferredoxin (fdr) (e.g., see Fig. 5b,c). While the free energy change under standard conditions suggests that this reaction is favorable only in reverse (i.e., ΔGnad/fd = 3.83 kcal85), there exists multiple experimental evidence alluding to the feasibility of electron transfer from NAD(P)H to ferredoxin86.
) to explore ways of co-utilizing methane and CO2 (or CO) towards acetate (Fig. 5). Additional designs provide pathways from acetate to the final products (Fig. 6). All designs show that the terminal acceptors exchanged electrons with a cofactor pair instead of directly catalyzing a reaction in the carbon-transfer network. Different cofactors were identified for the electron acceptors depending on the reduction reactions in the network (see Supplementary Text S1 for details). Note that a few of the designs require electron transfer between NADH/NADPH and ferredoxin for regeneration of reduced ferredoxin (fdr) (e.g., see Fig. 5b,c). While the free energy change under standard conditions suggests that this reaction is favorable only in reverse (i.e., ΔGnad/fd = 3.83 kcal85), there exists multiple experimental evidence alluding to the feasibility of electron transfer from NAD(P)H to ferredoxin86.
Network designs for conversion of methane and C1 co-reactant towards four C2+ target chemicals.
Metabolic network of synthesis of acetyl-CoA (accoa) from methane (CH4) and co-metabolite (CO2 or CO) is shown in Figure 5. Metabolic pathways proposed in previous studies are highlighted in blue while new designs are drawn in green.
Figure 5 shows three alternate routes for the conversion of three molecules of methane and one molecule of CO2 to two acetate molecules with  as the terminal electron acceptor. The smallest network (Fig. 5a) describes a functional reversal of the methanogenesis pathway where one molecule of methane and CO2 form acetyl-CoA using enzymes found in most methanogenic archaea and some methanotrophs78. However, in order to maintain the 1:1 ratio of methane and CO2 in the ACS reaction, one molecule of methane is oxidized to CO2 in a complex three-step cyclic route involving a functional reversal of the eastern branch of the Wood-Ljungdahl pathway (Fig. 5a). Alternate routes for oxidizing methane were also found that directly oxidize methyl-CoM to CO2 based on the methylamine cycle (Fig. 5b). The third design (Fig. 5c) bypasses the ACS and MTBA reactions by combining the two cycles described in Fig. 5a,b. Interestingly all the recruited enzymes (except for the terminal electron acceptors) are present in most anaerobic methanogens. This case study demonstrates how cofactor balances can become the dominant factor in synthetic pathway design. For example, the net reduction of 5-methyl tetrahydrofolate (5 mthf) to 5,10-methylene tetrahydrofolate is accomplished by two reactions running in opposite directions involving NAD and ferredoxin cofactors (Fig. 5a) to maintain overall balance of cofactors.
as the terminal electron acceptor. The smallest network (Fig. 5a) describes a functional reversal of the methanogenesis pathway where one molecule of methane and CO2 form acetyl-CoA using enzymes found in most methanogenic archaea and some methanotrophs78. However, in order to maintain the 1:1 ratio of methane and CO2 in the ACS reaction, one molecule of methane is oxidized to CO2 in a complex three-step cyclic route involving a functional reversal of the eastern branch of the Wood-Ljungdahl pathway (Fig. 5a). Alternate routes for oxidizing methane were also found that directly oxidize methyl-CoM to CO2 based on the methylamine cycle (Fig. 5b). The third design (Fig. 5c) bypasses the ACS and MTBA reactions by combining the two cycles described in Fig. 5a,b. Interestingly all the recruited enzymes (except for the terminal electron acceptors) are present in most anaerobic methanogens. This case study demonstrates how cofactor balances can become the dominant factor in synthetic pathway design. For example, the net reduction of 5-methyl tetrahydrofolate (5 mthf) to 5,10-methylene tetrahydrofolate is accomplished by two reactions running in opposite directions involving NAD and ferredoxin cofactors (Fig. 5a) to maintain overall balance of cofactors.
Figure 6 illustrates a few of the existing (in blue) and newly identified strategies (in green) for the production of four platform chemicals (i.e., 2,3-butanediol, 3-hydroxypropionate, 1-butanol and 1,3-propanediol62,81) each utilizing a different electron acceptor. For example, for 2,3-butanediol (23 but), while existing pathways (from pyruvate87) lose two carbon atoms for each molecule of 23 but, the identified pathways (Fig. 6a) preserve all carbon as lost CO2 is fixed back in the PFOR step. It is interesting to note that the identified pathway uses the same enzymes (except the MTA reaction) recruited for converting CO to 23 bdo in a recent study performed on three separate acetogenic clostridial species48 and functionally expressed in E. coli88. Three separate pathways were identified for 3-hydroxypropionate (3 hp) production all of which have been explored previously47,89,90 (Fig. 6b). Similarly, the shortest route for 1-butanol production (Fig. 6c) recapitulates existing strategies involving condensation of two molecules of acetyl-CoA by the accoa acetyltransferase (ACTR) followed by a functional reversal of the β-oxidation pathway45,91,92. A so far unexplored pathway is also suggested that combines the oxidative branch of TCA cycle with succinate-semialdehyde metabolism to reach 1-butanol (see Fig. 6c in green). For 1,3-propanediol (13 pdo) (Fig. 6d), the only identified pathway reduces acetyl-CoA back to glycerol, which is subsequently reduced to 13 pdo in three steps by the native reactions in some clostridial species93 or engineered enzymes found in E. coli and K. pneumonie (i.e., the DuPont pathway94). Our procedure could not identify an alternate pathway in E. coli95 where homoserine (hser) flux is routed towards 3-hydroxypropanal (3 hpa) by engineering the native glutamate dehydrogenase to be promiscuous towards homoserine. The reason is because the intermediate metabolite 4-hydroxy-2-oxobutyrate (4 hkbut) in the pathway as well as the reactions associated with the intermediate (see Fig. 6d in red) were absent in our database. Upon inclusion of the metabolite and the reactions, minFlux could identify this pathway as an alternate more energy efficient route for 13 pdo production.
In this study we identified and rank-ordered feasible electron acceptor pairs according to their methane oxidation potential. Unlike the previous example, thermodynamic feasibility and not elemental balances becomes the limiting factor in determining the optimum stoichiometric ratios in the overall reaction. minFlux identified relevant cofactor systems that coupled the methane utilization pathway with the terminal electron acceptors.
Discussion
In this paper we introduced a two-step computational procedure (optStoic + minRxn/minFlux) for designing de novo synthetic networks that match an overall stoichiometry of chemical transformation. Performance criteria on the designed pathways (e.g., carbon yield/ energy efficiency, pathway ΔG etc.) can systematically be imposed to rank-order synthetic pathways according to the design objective. The case studies highlight the potential of this procedure for designing a thermodynamically feasible overall conversion stoichiometry, selecting the optimum combination of co-metabolites and co-products and constructing non-intuitive synthetic biological routes for the overall conversion. We compared the optimal pathways identified here with two existing pathway design tools (Chou et al.96 and Bar-Even et al.31) for all three case studies. The results showed that the depth-first graph search algorithm for Chou et al.96 identified only linear paths connecting the primary substrate to the primary product for all the case studies, while failing to identify any of the carbon-conserving cyclic networks (Supplementary Text S1, Figure S6). The Bar-Even et al.31 approach successfully recapitulated the NOG cycle (Case Study 1), however, cofactor imbalances were introduced for the last two studies (Supplementary Text S1, Figure S6). The comparison demonstrates that designing first an overall stoichiometry enables homing in on only the designs with maximum carbon efficiency, particularly for conversions involving multiple substrates (or products).
Existing databases such as MetRxn49 or KEGG97 span a very large number of intermediate metabolites that can be produced from the reacting metabolites. In contrast, the number of terminal pathways towards target products tends to be much more limited. For example, acetyl-CoA participates in 153 reactions, whereas 13 pdo and phloroglucinol are involved in one and two reactions, respectively. Therefore, most of the novel network designs suggested by minRxn/minFlux stemmed from alternate intermediate metabolites and ways of producing them. Inclusion of additional metabolites and reactions (especially involved in the production/consumption of terminal metabolites) in the database could allow for the identification of additional conversion pathways (e.g., 13 pdo production in Case Study 3). Another promising way of expanding the diversity of designs could be to consider hypothetical biotransformations generated by successively applying reaction operators on metabolites42,98. For example, in a recent work for synthesizing platform chemicals in E. coli, GEM-Path41 suggested a pathway for 13 pdo production from malate that involved two de novo reactions. By combining minRxn/minFlux with compilations of hypothetical reactions and metabolites (e.g., BNICE98, GEM-Path41, Pertusi et al.40) the scope and diversity of designed synthetic networks would increase significantly. In addition, kinetic and toxicity information99,100 can be incorporated within minRxn/minFlux to further restrict the design space by avoiding kinetic bottlenecks and toxic intermediates. For example, maximum enzyme activity information could be used in addition to thermodynamics to set the bounds for the reaction fluxes.
Methods
The detailed description of the two-step path-finding procedure is described in the following sections.
Step 1: Determining optimal reactant and product combination and overall stoichiometry
The procedure begins with an optimization task that establishes the maximum achievable yields of the envisioned bioconversion subject to thermodynamic restrictions. This optimization task requires access to a database of metabolites along with specific data for each one of them. In this paper we assembled a database of 5,753 metabolites extracted from the MetRxn database49 (see Supplementary Data File S3). The following parameters are introduced that keep track of the elemental composition, charge information and free energy of formation data needed to describe the optimization problem:
niq: # of atoms of element q in metabolite i
ei: Charge of metabolite i101
 : Transformed free energy of formation (at 25 °C and 0.1 M ionic strength) of metabolite i102
: Transformed free energy of formation (at 25 °C and 0.1 M ionic strength) of metabolite i102
where i = 1, …, N is the set I of metabolites present in the database and  is the set of elements found in the metabolites (i.e., C, O, N, P, S, H, Fe, etc.) (see Supplementary Data File S3 for dataset).
is the set of elements found in the metabolites (i.e., C, O, N, P, S, H, Fe, etc.) (see Supplementary Data File S3 for dataset).
For the sake of simplicity of presentation the optimization formulation is derived for the following bimolecular stoichiometry as shown in Fig. 1:

Using this representation either all the metabolites participating in the reaction are known a priori implying that all coefficients are positive and non-zero, or the presence of some of them is uncertain in which case the corresponding stoichiometric coefficients are allowed to assume a value of zero. Only one of the stoichiometric coefficients needs to be fixed to a finite value to provide a scaling for the remaining ones. Generally, we fix either the coefficient of the limiting carbon substrate or the primary product. By fixing this coefficient the presence of the corresponding reactant or product in the overall conversion is guaranteed. Note that setting the stoichiometric coefficient of a one-carbon molecule to one may not ensure that all other coefficients can assume integer values due to the balances on all other elements. However, all determined coefficients could be suitably scaled up to obtain an integer-only stoichiometry for all metabolites. The performance criteria of the overall conversion may involve (i) maximum yield for primary product B (i.e. max b while a = fixed), (ii) maximum co-utilization of free reactant C (max c, b = fixed) for a given product yield, (iii) minimum formation of by-product D (min d while b = fixed) or combinations thereof. The overall optimization formulation for Step 1 is as follows (optStoic):






In formulation (optStoic),  is a function of the overall stoichiometric coefficients quantifying a performance objective, Constraint (1) and (2) impose elemental and charge balances on the overall conversion respectively, while Constraint (3) imposes overall thermodynamic feasibility
is a function of the overall stoichiometric coefficients quantifying a performance objective, Constraint (1) and (2) impose elemental and charge balances on the overall conversion respectively, while Constraint (3) imposes overall thermodynamic feasibility  .
.  quantifies the amount of “extra”
quantifies the amount of “extra”  available for the designed stoichiometry. The stoichiometry of the basis metabolite (usually the limiting carbon source) is set to a value of one. Constraint (4) generalizes the description of this scaling decision. Stoichiometric coefficients a, b, c, d can be declared as integer or real depending on the adopted scaling of the overall conversion. It is straightforward to extend the optStoic formulation to account for more than two reactants and two products. In fact, a comprehensive list of putative co-reactants and co-products could be designed in the overall stoichiometry and then rely on the optStoic optimization problem to identify the optimal combination of co-reactants and co-products. Additional binary variables, associated with each metabolite from set I, are included in the formulation to decide whether the respective metabolite should be a part of the overall stoichiometry or not. A negative value for a stoichiometric coefficient declares a metabolite as a reactant while a positive value defines it as a product. Here, both the participating metabolites and their respective coefficients are decision variables and the modified optStoic formulation is a mixed integer linear programming (MILP) problem or an integer programming problem (IP) depending on whether the stoichiometric coefficients are declared as real or integer variables respectively.
available for the designed stoichiometry. The stoichiometry of the basis metabolite (usually the limiting carbon source) is set to a value of one. Constraint (4) generalizes the description of this scaling decision. Stoichiometric coefficients a, b, c, d can be declared as integer or real depending on the adopted scaling of the overall conversion. It is straightforward to extend the optStoic formulation to account for more than two reactants and two products. In fact, a comprehensive list of putative co-reactants and co-products could be designed in the overall stoichiometry and then rely on the optStoic optimization problem to identify the optimal combination of co-reactants and co-products. Additional binary variables, associated with each metabolite from set I, are included in the formulation to decide whether the respective metabolite should be a part of the overall stoichiometry or not. A negative value for a stoichiometric coefficient declares a metabolite as a reactant while a positive value defines it as a product. Here, both the participating metabolites and their respective coefficients are decision variables and the modified optStoic formulation is a mixed integer linear programming (MILP) problem or an integer programming problem (IP) depending on whether the stoichiometric coefficients are declared as real or integer variables respectively.
The impact of cellular growth requirements on the flux allocation towards the target metabolite can be directly assessed by updating the overall stoichiometry to include biomass, growth (and non-growth) associated maintenance ATP as additional product metabolites:

Here positive variable δ is the cellular growth coefficient and biomass is represented as a weighted (by coeffk) sum of all the biomass precursors Mk (i.e., amino acids, lipids, cofactors as well as ATP requirements for cellular growth). Constraints for elemental and charge balances and thermodynamic feasibility limitations are updated accordingly in optStoic:



The trade-off between product yield and biomass formation can be assessed by fixing δ at different levels between zero and maximum growth and subsequently maximizing the target product coefficient.
Profit margin considerations (e.g., by using bulk market price of chemicals103) can also be imposed in the optStoic formulation by specifying that the product prices exceed the reactant costs by a pre-specified margin profitmin.

where pri are the per mole prices of reactants/products i. Alternatively this margin could become the objective function that is maximized if an economic criterion is used to select reactant/product pairs. Trade-offs between the overall conversion stoichiometry and the negativity of the overall free energy change can be drawn by varying the value of ΔGmin. For large values of ΔGmin overall conversions are obtained with a high thermodynamic driving force. As ΔGmin is throttled back closer to zero more yield efficient conversions are obtained at the expense of a lower thermodynamic driving force that may limit flux per enzyme loading. Given that biomass formation is an endergonic process  it is important to keep ΔGmin above the value needed for the desired growth. For example, for the iAF1260 metabolic model we find that the production of all constituents of biomass require a ΔG of 492.77 kcal g−1 biomass. Additional reserves for ΔG are needed to account for polymerization free energy costs of the biomass precursors not captured in the biomass equation. Alternatively, the overall stoichiometry could be expanded to directly include biomass, growth and non-growth associated maintenance ATP as product metabolites as described above.
it is important to keep ΔGmin above the value needed for the desired growth. For example, for the iAF1260 metabolic model we find that the production of all constituents of biomass require a ΔG of 492.77 kcal g−1 biomass. Additional reserves for ΔG are needed to account for polymerization free energy costs of the biomass precursors not captured in the biomass equation. Alternatively, the overall stoichiometry could be expanded to directly include biomass, growth and non-growth associated maintenance ATP as product metabolites as described above.
Step 2: Identifying reactions that conform to the identified overall stoichiometry
The second step identifies the smallest network of reactions that apportions the elemental composition of the substrates to the desired products in their corresponding stoichiometric ratios as determined in Step 1 (Fig. 1). To this end we extracted a set of mass and charge balanced reactions J (i.e., 6,871 reactions) from the MetRxn database49 involving metabolites from set I (see Supplementary Data File S4 for datasets) with additional exchange reactions for only the metabolites present in the overall stoichiometry to allow for their uptake and export, respectively. The optimization formulation for identifying the minimal number of reaction to match the identified stoichiometry requires the definition of the following parameters:
Sij: Stoichiometry matrix that describes the coefficient of metabolite i in reaction j
 ,
,  : Lower and upper bound estimates for the ΔG of each reaction
: Lower and upper bound estimates for the ΔG of each reaction
(see Supplementary Data File S4 for dataset)
LBj, UBj: Lower and upper bounds on the flux of each reaction j
The change in free energy ΔG of a reaction is a function of the non-standard activities of the participating metabolites as follows:

where R is the gas constant and T is the temperature.  is the free energy change of the reaction under standard conditions. Note that Q is the reaction quotient expressed as the ratio of the product of the activities (approximated by their molar concentration in an aqueous solution) of the products raised to their stoichiometric coefficient to that of the reactants. The reaction quotient Q for the overall conversion aA + cC → bB + dD is:
is the free energy change of the reaction under standard conditions. Note that Q is the reaction quotient expressed as the ratio of the product of the activities (approximated by their molar concentration in an aqueous solution) of the products raised to their stoichiometric coefficient to that of the reactants. The reaction quotient Q for the overall conversion aA + cC → bB + dD is:

where the expressions within brackets are the molar concentrations of each participating metabolite. The minimum  and maximum
and maximum  bounds on ΔG for each reaction in J are obtained by varying the concentration of the metabolites participating in the reaction by 1,000 fold of their transformed standard concentration (see Supplementary Data File S3). The wide range was chosen as a conservative estimate to allow for extreme fluctuations in intracellular metabolite concentrations in microorganisms (e.g., Bennet et al.104 reported intracellular metabolite ranges in exponentially growing E. coli to vary between 10−3–102 mM). Reaction bounds LBj and UBj are determined according to the following rule:
bounds on ΔG for each reaction in J are obtained by varying the concentration of the metabolites participating in the reaction by 1,000 fold of their transformed standard concentration (see Supplementary Data File S3). The wide range was chosen as a conservative estimate to allow for extreme fluctuations in intracellular metabolite concentrations in microorganisms (e.g., Bennet et al.104 reported intracellular metabolite ranges in exponentially growing E. coli to vary between 10−3–102 mM). Reaction bounds LBj and UBj are determined according to the following rule:

where M is a large positive value (i.e., M = 1,000) in relation the exchange flux of the metabolites of the overall stoichiometry (from Step 1). Additional information on directionality of reactions obtained from literature can be used, whenever available, to further constrain LBjand UBj. The directionality for 4,447 reactions (out of 6,871 within set J) was assigned by this procedure while the remaining 2,424 that lacked the free energy of formation for one or more metabolite were treated as reversible. Out of the 4,447 analyzed reactions, 2,205 were found to be irreversible whereas 2,242 were reversible. The identification of the minimal set of reactions that can match the desired overall stoichiometry (found after Step 1) is formulated as the following MILP (minRxn) problem:





Binary variables yj defined as

control the addition (or not) of reaction j in the overall network. The objective function involves the minimization of the sum of yj’s (Constraint 12) to extract the minimum number of reactions that can support the desired overall stoichiometry (optStoic) of Step 1. Constraint (13) ensures that all metabolites, including cofactors, are used in a stoichiometrically balanced manner. Constraint (14) sets the flux of the exchange reactions (i.e., for A, B, C and D) equal to their respective stoichiometric coefficients thus matching the overall desired stoichiometry (from Step 1) and providing a flux scaling. Constraint (15) ensures that reaction j is removed from the designed network when yj is equal to zero. Networks for different overall stoichiometries (from Step 1) can be obtained and contrasted for their overall performance metrics. The use of integer cut constraints to (i) disallow previously identified solutions and (ii) search for alternate optimal as well as sub-optimal solutions can be used to exhaustively explore all possible ways of linking reactants to products (Constraint 16).

where k = 1, …, K is the set previously of explored solutions.
The resulting (minRxn) MILP formulation can be computationally challenging to solve as it involves as many as 6,871 binary variables associated with all the reactions in set J. A related LP formulation (minFlux) that is significantly (i.e., up to three orders of magnitude) less computationally taxing can be solved as a surrogate of minRxn. In contrast to minRxn that directly minimizes the total number of reactions in the designed network, minFlux minimizes the total metabolic flux of the chosen reactions. This modified objective function could be viewed as an approximation of the total enzyme-load imposed on the organism105:







In minFlux, the sum of the absolute values of the reaction fluxes denoted by xj is minimized (Constraint 17). Constraints (13) and (14) are the same as in (minRxn) formulation whereas Constraint (18) imposes bounds on fluxes without multiplication with a binary variable. Constraints (19) and (20) ensure that xj is greater than both vj and −vj. The minimization operator in the objective function ensures that for every j either Constraint (19) or (20) becomes active.
Alternate optimal (as well as suboptimal) basic flux combinations can also be explored by preventing all nonzero basic variables from an earlier solution k from reappearing in subsequent flux combinations (see Lee et al.106 for details). In short, we first reorganize minFlux in standard form107 and transform all the variables (i.e., xj and vj) to positive variable sl (where L is the set of variables for problem in standard form). Subsequently, a set of integer cut constraints similar to the ones described for formulation (minRxn) can be constructed. Binary variables ul denote the presence of nonzero basic variable l in a previously identified solution k. The following constraints prevents the reappearance of a previously found basic feasible solution:


where  is a small positive value
is a small positive value  that ensures that sl is nonzero when ul = 1. It is important to stress that the addition of integer cuts converts the LP (minFlux) formulation to an MILP problem. Nevertheless, it is can be solved significantly faster (about two orders of magnitude) than minRxn as it involves much fewer binary variables.
that ensures that sl is nonzero when ul = 1. It is important to stress that the addition of integer cuts converts the LP (minFlux) formulation to an MILP problem. Nevertheless, it is can be solved significantly faster (about two orders of magnitude) than minRxn as it involves much fewer binary variables.
Additional constraints can be added in either minRxn or minFlux optimization formulations to maintain the total number of reactions with a positive standard change in free energy at a minimum (e.g., less than pt):



where uj is a binary variable which is defined as:

Reactions with a positive standard change in free energy may require the accumulation of a significant reactant metabolite pool to drive the reaction forward. This is generally undesirable as it may throttle back the flux in the overall pathway by triggering cellular toxicity and/or pathway substrate inhibition.
In addition, formulations minRxn or minFlux can be augmented to control the number of organisms from which reactions are sourced in the construction of the conversion network to less than po.



Here, parameter orgoj has a value of one if reaction j is present in organism o and zero otherwise. Using binary variable ro, Constraint (26) ensures that a reaction j cannot carry any flux unless it is present in at least one organism o (i.e.,  ). Constraint (27) sets an upper bound po on the number of organisms contributing reactions. One can avoid selecting the host organism a priori, thus allowing the optimization formulation to select the production host(s) best suited to construct the synthetic network. In addition, the definition of set O can be altered accordingly to minimize diversity in chosen genus instead of individual organisms. Alternatively, the production host could be pre-specified and then restrict the total number of heterologous reactions.
). Constraint (27) sets an upper bound po on the number of organisms contributing reactions. One can avoid selecting the host organism a priori, thus allowing the optimization formulation to select the production host(s) best suited to construct the synthetic network. In addition, the definition of set O can be altered accordingly to minimize diversity in chosen genus instead of individual organisms. Alternatively, the production host could be pre-specified and then restrict the total number of heterologous reactions.
Additional Information
How to cite this article: Chowdhury, A. and Maranas, C. D. Designing overall stoichiometric conversions and intervening metabolic reactions. Sci. Rep. 5, 16009; 10.1038/srep16009 (2015).
References
Cho, C., Choi, S. Y., Luo, Z. W. & Lee, S. Y. Recent advances in microbial production of fuels and chemicals using tools and strategies of systems metabolic engineering. Biotechnol. Adv., 10.1016/j.biotechadv.2014.11.006 (2014).
Curran, K. A. & Alper, H. S. Expanding the chemical palate of cells by combining systems biology and metabolic engineering. Metab. Eng. 14, 289–297, 10.1016/j.ymben.2012.04.006 (2012).
Liu, L., Redden, H. & Alper, H. S. Frontiers of yeast metabolic engineering: diversifying beyond ethanol and Saccharomyces. Curr. Opin. Biotechnol. 24, 1023–1030, 10.1016/j.copbio.2013.03.005 (2013).
Kelwick, R., MacDonald, J. T., Webb, A. J. & Freemont, P. Developments in the tools and methodologies of synthetic biology. Front. Bioeng. Biotechnol. 2, 60, 10.3389/fbioe.2014.00060 (2014).
Farasat, I. et al. Efficient search, mapping and optimization of multi-protein genetic systems in diverse bacteria. Mol. Syst. Biol. 10, 731, 10.15252/msb.20134955 (2014).
Balzer, S. et al. A comparative analysis of the properties of regulated promoter systems commonly used for recombinant gene expression in Escherichia coli. Microb. Cell Fact. 12, 26, 10.1186/1475-2859-12-26 (2013).
Salis, H. M. The ribosome binding site calculator. Methods Enzymol. 498, 19–42, 10.1016/B978-0-12-385120-8.00002-4 (2011).
Xu, P., Vansiri, A., Bhan, N. & Koffas, M. A. ePathBrick: a synthetic biology platform for engineering metabolic pathways in E. coli. ACS Synth. Biol. 1, 256–266, 10.1021/sb300016b (2012).
Ongley, S. E., Bian, X., Neilan, B. A. & Muller, R. Recent advances in the heterologous expression of microbial natural product biosynthetic pathways. Nat. Prod. Rep. 30, 1121–1138, 10.1039/c3np70034h (2013).
Richter, K. & Gescher, J. The molecular toolbox for chromosomal heterologous multiprotein expression in Escherichia coli. Biochem. Soc. Trans. 40, 1222–1226, 10.1042/BST20120143 (2012).
Xu, P., Li, L., Zhang, F., Stephanopoulos, G. & Koffas, M. Improving fatty acids production by engineering dynamic pathway regulation and metabolic control. Proc. Natl. Acad. Sci. USA 111, 11299–11304, 10.1073/pnas.1406401111 (2014).
Zhang, F., Carothers, J. M. & Keasling, J. D. Design of a dynamic sensor-regulator system for production of chemicals and fuels derived from fatty acids. Nat. Biotechnol. 30, 354–359, 10.1038/nbt.2149 (2012).
Bonde, M. T. et al. Direct Mutagenesis of Thousands of Genomic Targets Using Microarray-Derived Oligonucleotides. ACS Synth. Biol., 10.1021/sb5001565 (2014).
Sander, J. D. & Joung, J. K. CRISPR-Cas systems for editing, regulating and targeting genomes. Nat. Biotechnol. 32, 347–355, 10.1038/nbt.2842 (2014).
Qi, L. S. et al. Repurposing CRISPR as an RNA-guided platform for sequence-specific control of gene expression. Cell 152, 1173–1183, 10.1016/j.cell.2013.02.022 (2013).
Na, D. et al. Metabolic engineering of Escherichia coli using synthetic small regulatory RNAs. Nat. Biotechnol. 31, 170–174, 10.1038/nbt.2461 (2013).
Keasling, J. D. Manufacturing molecules through metabolic engineering. Science 330, 1355–1358, 10.1126/science.1193990 (2010).
Chowdhury, A., Zomorrodi, A. R. & Maranas, C. D. Bilevel optimization techniques in computational strain design. Comput. Chem. Eng. 72, 363–372, 10.1016/j.compchemeng.2014.06.007 (2015).
Fong, S. S. Computational approaches to metabolic engineering utilizing systems biology and synthetic biology. Comput. Struct. Biotechnol. J. 11, 28–34, 10.1016/j.csbj.2014.08.005 (2014).
Zomorrodi, A. R., Suthers, P. F., Ranganathan, S. & Maranas, C. D. Mathematical optimization applications in metabolic networks. Metab. Eng. 14, 672–686, 10.1016/j.ymben.2012.09.005 (2012).
Chowdhury, A., Zomorrodi, A. R. & Maranas, C. D. k-OptForce: integrating kinetics with flux balance analysis for strain design. PLoS Comput. Biol. 10, e1003487, 10.1371/journal.pcbi.1003487 (2014).
Khodayari, A., Chowdhury, A. & Maranas, C. D. Succinate Overproduction: A Case Study of Computational Strain Design Using a Comprehensive Escherichia coli Kinetic Model. Front. Bioeng. Biotechnol. 2, 76, 10.3389/fbioe.2014.00076 (2014).
Zanghellini, J., Ruckerbauer, D. E., Hanscho, M. & Jungreuthmayer, C. Elementary flux modes in a nutshell: properties, calculation and applications. Biotechnol. J. 8, 1009–1016, 10.1002/biot.201200269 (2013).
Klamt, S., Stelling, J., Ginkel, M. & Gilles, E. D. FluxAnalyzer: exploring structure, pathways and flux distributions in metabolic networks on interactive flux maps. Bioinformatics 19, 261–269 (2003).
Pfeiffer, T., Sanchez-Valdenebro, I., Nuno, J. C., Montero, F. & Schuster, S. METATOOL: for studying metabolic networks. Bioinformatics 15, 251–257 (1999).
Trinh, C. T., Unrean, P. & Srienc, F. Minimal Escherichia coli cell for the most efficient production of ethanol from hexoses and pentoses. Appl. Environ. Microbiol. 74, 3634–3643, 10.1128/AEM.02708-07 (2008).
Ballerstein, K., von Kamp, A., Klamt, S. & Haus, U. U. Minimal cut sets in a metabolic network are elementary modes in a dual network. Bioinformatics 28, 381–387, 10.1093/bioinformatics/btr674 (2012).
Machado, D., Soons, Z., Patil, K. R., Ferreira, E. C. & Rocha, I. Random sampling of elementary flux modes in large-scale metabolic networks. Bioinformatics 28, i515–i521, 10.1093/bioinformatics/bts401 (2012).
Rezola, A. et al. Exploring metabolic pathways in genome-scale networks via generating flux modes. Bioinformatics 27, 534–540, 10.1093/bioinformatics/btq681 (2011).
Bordbar, A. et al. Minimal metabolic pathway structure is consistent with associated biomolecular interactions. Mol. Syst. Biol. 10, 737, 10.15252/msb.20145243 (2014).
Bar-Even, A., Noor, E., Lewis, N. E. & Milo, R. Design and analysis of synthetic carbon fixation pathways. Proc. Natl. Acad. Sci. USA 107, 8889–8894, 10.1073/pnas.0907176107 (2010).
Kim, J., Reed, J. L. & Maravelias, C. T. Large-scale bi-level strain design approaches and mixed-integer programming solution techniques. PloS One 6, e24162, 10.1371/journal.pone.0024162 (2011).
Pharkya, P., Burgard, A. P. & Maranas, C. D. OptStrain: a computational framework for redesign of microbial production systems. Genome Res. 14, 2367–2376, 10.1101/gr.2872004 (2004).
Vieira, G., Carnicer, M., Portais, J. C. & Heux, S. FindPath: a Matlab solution for in silico design of synthetic metabolic pathways. Bioinformatics 30, 2986–2988, 10.1093/bioinformatics/btu422 (2014).
Deville, Y., Gilbert, D., van Helden, J. & Wodak, S. J. An overview of data models for the analysis of biochemical pathways. Brief. Bioinform. 4, 246–259 (2003).
Rodrigo, G., Carrera, J., Prather, K. J. & Jaramillo, A. DESHARKY: automatic design of metabolic pathways for optimal cell growth. Bioinformatics 24, 2554–2556, 10.1093/bioinformatics/btn471 (2008).
McClymont, K. & Soyer, O. S. Metabolic tinker: an online tool for guiding the design of synthetic metabolic pathways. Nucleic Acids Res. 41, e113, 10.1093/nar/gkt234 (2013).
Faust, K., Dupont, P., Callut, J. & van Helden, J. Pathway discovery in metabolic networks by subgraph extraction. Bioinformatics 26, 1211–1218, 10.1093/bioinformatics/btq105 (2010).
Wu, D., Wang, Q., Assary, R. S., Broadbelt, L. J. & Krilov, G. A computational approach to design and evaluate enzymatic reaction pathways: application to 1-butanol production from pyruvate. J. Chem. Inf. Model. 51, 1634–1647, 10.1021/ci2000659 (2011).
Pertusi, D. A., Stine, A. E., Broadbelt, L. J. & Tyo, K. E. Efficient searching and annotation of metabolic networks using chemical similarity. Bioinformatics 31, 1016–1024, 10.1093/bioinformatics/btu760 (2015).
Campodonico, M. A., Andrews, B. A., Asenjo, J. A., Palsson, B. O. & Feist, A. M. Generation of an atlas for commodity chemical production in Escherichia coli and a novel pathway prediction algorithm, GEM-Path. Metab. Eng. 25, 140–158, 10.1016/j.ymben.2014.07.009 (2014).
Moura, M., Broadbelt, L. & Tyo, K. Computational tools for guided discovery and engineering of metabolic pathways. Methods Mol. Biol. 985, 123–147, 10.1007/978-1-62703-299-5_8 (2013).
Jouhten, P. Metabolic modelling in the development of cell factories by synthetic biology. Comput. Struct. Biotechnol. J. 3, e201210009, 10.5936/csbj.201210009 (2012).
Bogorad, I. W., Lin, T. S. & Liao, J. C. Synthetic non-oxidative glycolysis enables complete carbon conservation. Nature 502, 693–697, 10.1038/nature12575 (2013).
Atsumi, S. et al. Metabolic engineering of Escherichia coli for 1-butanol production. Metab. Eng. 10, 305–311, 10.1016/j.ymben.2007.08.003 (2008).
Bogorad, I. W. et al. Building carbon-carbon bonds using a biocatalytic methanol condensation cycle. Proc. Natl. Acad. Sci. USA 111, 15928–15933, 10.1073/pnas.1413470111 (2014).
Borodina, I. et al. Establishing a synthetic pathway for high-level production of 3-hydroxypropionic acid in Saccharomyces cerevisiae via beta-alanine. Metab. Eng. 27, 57–64, 10.1016/j.ymben.2014.10.003 (2015).
Kopke, M. et al. 2,3-butanediol production by acetogenic bacteria, an alternative route to chemical synthesis, using industrial waste gas. Appl. Environ. Microbiol. 77, 5467–5475, 10.1128/AEM.00355-11 (2011).
Kumar, A., Suthers, P. F. & Maranas, C. D. MetRxn: a knowledgebase of metabolites and reactions spanning metabolic models and databases. BMC Bioinformatics 13, 6, 10.1186/1471-2105-13-6 (2012).
Flamholz, A., Noor, E., Bar-Even, A., Liebermeister, W. & Milo, R. Glycolytic strategy as a tradeoff between energy yield and protein cost. Proc. Natl. Acad. Sci. USA 110, 10039–10044, 10.1073/pnas.1215283110 (2013).
Verhees, C. H. et al. The unique features of glycolytic pathways in Archaea. Biochem. J. 375, 231–246, 10.1042/BJ20021472 (2003).
Aristilde, L., Lewis, I. A., Park, J. O. & Rabinowitz, J. D. Hierarchy in Pentose Sugar Metabolism in Clostridium Acetobutylicum. Appl. Environ. Microbiol., 10.1128/AEM.03199-14 (2014).
O’Donnell, M. M., O’Toole, P. W. & Ross, R. P. Catabolic flexibility of mammalian-associated lactobacilli. Microb. Cell Fact. 12, 48, 10.1186/1475-2859-12-48 (2013).
Wiegant, W. M. & Debont, J. A. M. A New Route for Ethylene-Glycol Metabolism in Mycobacterium-E44. J. Gen. Microbiol. 120, 325–331 (1980).
Gawand, P., Hyland, P., KEknis, A., Martin, V. J. J. & Mahadevan, R. Novel approach to engineer strains for simultaneous sugar utilization. Metab. Eng. 20, 63–72 (2013).
Tracy, B. P., Jones, S. W., Fast, A. G., Indurthi, D. C. & Papoutsakis, E. T. Clostridia: the importance of their exceptional substrate and metabolite diversity for biofuel and biorefinery applications. Curr. Opin. Biotechnol. 23, 364–381, 10.1016/j.copbio.2011.10.008 (2012).
Huang, H., Wang, S., Moll, J. & Thauer, R. K. Electron bifurcation involved in the energy metabolism of the acetogenic bacterium Moorella thermoacetica growing on glucose or H2 plus CO2. J. Bacteriol. 194, 3689–3699, 10.1128/JB.00385-12 (2012).
Ragsdale, S. W. Pyruvate ferredoxin oxidoreductase and its radical intermediate. Chem. Rev. 103, 2333–2346, 10.1021/cr020423e (2003).
Feist, A. M. et al. A genome-scale metabolic reconstruction for Escherichia coli K-12 MG1655 that accounts for 1260 ORFs and thermodynamic information. Mol. Syst. Biol. 3, 121, 10.1038/msb4100155 (2007).
Olah, G. A. Beyond oil and gas: The methanol economy. Angew. Chem. Int. Ed. Engl. 44, 2636–2639, 10.1002/Anie.200462121 (2005).
Kozlowski, J. T. & Davis, R. J. Heterogeneous Catalysts for the Guerbet Coupling of Alcohols. ACS Catal. 3, 1588–1600, 10.1021/Cs400292f (2013).
Jang, Y. S. et al. Bio-based production of C2-C6 platform chemicals. Biotechnol. Bioeng. 109, 2437–2459, 10.1002/bit.24599 (2012).
Singh, I. P., Sidana, J., Bansal, P. & Foley, W. J. Phloroglucinol compounds of therapeutic interest: global patent and technology status. Expert Opin. Ther. Pat. 19, 847–866, 10.1517/13543770902916614 (2009).
Wang, L., Chen, H., Zhang, T., Zhang, J. & Yang, L. Synthesis, characterization, thermal and explosive properties of potassium salts of trinitrophloroglucinol. J. Hazard. Mater. 147, 576–580, 10.1016/j.jhazmat.2007.01.043 (2007).
Kato, N., Yurimoto, H. & Thauer, R. K. The physiological role of the ribulose monophosphate pathway in bacteria and archaea. Biosci. Biotechnol. Biochem. 70, 10–21, 10.1271/bbb.70.10 (2006).
Bender, R. A. Regulation of the histidine utilization (hut) system in bacteria. Microbiol. Mol. Biol. Rev. 76, 565–584, 10.1128/MMBR.00014-12 (2012).
Alissandratos, A., Kim, H. K. & Easton, C. J. Formate production through biocatalysis. Bioengineered 4, 348–350, 10.4161/bioe.25360 (2013).
Mainguet, S. E., Gronenberg, L. S., Wong, S. S. & Liao, J. C. A reverse glyoxylate shunt to build a non-native route from C4 to C2 in Escherichia coli. Metab. Eng. 19, 116–127, 10.1016/j.ymben.2013.06.004 (2013).
Heinrich, D., Raberg, M. & Steinbuchel, A. Synthesis of poly(3-hydroxybutyrate-co-3-hydroxyvalerate) from unrelated carbon sources in engineered Rhodospirillum rubrum. FEMS Microbiol. Lett., 10.1093/femsle/fnv038 (2015).
Zhang, J., Gao, X., Hong, P. H., Li, Z. J. & Tan, T. W. Enhanced production of poly-3-hydroxybutyrate by Escherichia coli over-expressing multiple copies of NAD kinase integrated in the host genome. Biotechnol. Lett., 10.1007/s10529-015-1797-1 (2015).
Buchholz, J. et al. Platform engineering of Corynebacterium glutamicum with reduced pyruvate dehydrogenase complex activity for improved production of L-lysine, L-valine and 2-ketoisovalerate. Appl. Environ. Microbiol. 79, 5566–5575, 10.1128/AEM.01741-13 (2013).
Yang, F. & Cao, Y. Biosynthesis of phloroglucinol compounds in microorganisms–review. Appl. Microbiol. Biotechnol. 93, 487–495, 10.1007/s00253-011-3712-6 (2012).
Blum, T. & Kohlbacher, O. MetaRoute: fast search for relevant metabolic routes for interactive network navigation and visualization. Bioinformatics 24, 2108–2109, 10.1093/bioinformatics/btn360 (2008).
Carbonell, P., Parutto, P., Herisson, J., Pandit, S. B. & Faulon, J. L. XTMS: pathway design in an eXTended metabolic space. Nucleic Acids Res. 42, W389–394, 10.1093/nar/gku362 (2014).
EIA, U. (ed Washington US Department of Energy/EIA, DC) (2013).
Haynes, C. A. & Gonzalez, R. Rethinking biological activation of methane and conversion to liquid fuels. Nat. Chem. Biol. 10, 331–339, 10.1038/nchembio.1509 (2014).
Cui, M., Ma, A., Qi, H., Zhuang, X. & Zhuang, G. Anaerobic oxidation of methane: an “active” microbial process. Microbiologyopen 4, 1–11, 10.1002/mbo3.232 (2015).
Mueller, T. J. et al. Methane oxidation by anaerobic archaea for conversion to liquid fuels. J. Ind. Microbiol. Biotechnol. 42, 391–401, 10.1007/s10295-014-1548-7 (2015).
Haroon, M. F. et al. Anaerobic oxidation of methane coupled to nitrate reduction in a novel archaeal lineage. Nature 500, 567–570, 10.1038/nature12375 (2013).
Lovley, D. R. & Phillips, E. J. Novel mode of microbial energy metabolism: organic carbon oxidation coupled to dissimilatory reduction of iron or manganese. Appl. Environ. Microbiol. 54, 1472–1480 (1988).
de Jong, E., Higson, A., Walsh, P. & Wellisch, M. Bio-based chemicals value added products from biorefineries. (IEA Bioenergy, Task42 Biorefinery, 2012).
Conrado, R. J. & Gonzalez, R. Chemistry. Envisioning the bioconversion of methane to liquid fuels. Science 343, 621–623, 10.1126/science.1246929 (2014).
Orphan, V. J. et al. Comparative analysis of methane-oxidizing archaea and sulfate-reducing bacteria in anoxic marine sediments. Appl. Environ. Microbiol. 67, 1922–1934, 10.1128/AEM.67.4.1922-1934.2001 (2001).
Valentine, D. L. Biogeochemistry and microbial ecology of methane oxidation in anoxic environments: a review. Antonie Van Leeuwenhoek 81, 271–282 (2002).
Alberty, R. A. Calculation of standard transformed formation properties of biochemical reactants and standard apparent reduction potentials of half reactions. Arch. Biochem. Biophys. 358, 25–39, 10.1006/abbi.1998.0831 (1998).
Petitdemange, H., Cherrier, C., Raval, R. & Gay, R. Regulation of the NADH and NADPH-ferredoxin oxidoreductases in clostridia of the butyric group. Biochim. Biophys. Acta 421, 334–337 (1976).
Xiao, Z. & Lu, J. R. Strategies for enhancing fermentative production of acetoin: a review. Biotechnol. Adv. 32, 492–503, 10.1016/j.biotechadv.2014.01.002 (2014).
Kopke, M. et al. Reconstruction of an acetogenic 2,3-butanediol pathway involving a novel NADPH-dependent primary-secondary alcohol dehydrogenase. Appl. Environ. Microbiol. 80, 3394–3403, 10.1128/AEM.00301-14 (2014).
Honjo, H., Tsuruno, K., Tatsuke, T., Sato, M. & Hanai, T. Dual synthetic pathway for 3-hydroxypropionic acid production in engineered Escherichia coli. J. Biosci. Bioeng., 10.1016/j.jbiosc.2014.12.023 (2015).
Rathnasingh, C. et al. Production of 3-hydroxypropionic acid via malonyl-CoA pathway using recombinant Escherichia coli strains. J. Biotechnol. 157, 633–640, 10.1016/j.jbiotec.2011.06.008 (2012).
Dellomonaco, C., Clomburg, J. M., Miller, E. N. & Gonzalez, R. Engineered reversal of the beta-oxidation cycle for the synthesis of fuels and chemicals. Nature 476, 355–359, 10.1038/nature10333 (2011).
Lim, J. H., Seo, S. W., Kim, S. Y. & Jung, G. Y. Model-driven rebalancing of the intracellular redox state for optimization of a heterologous n-butanol pathway in Escherichia coli. Metab. Eng. 20, 56–62, 10.1016/j.ymben.2013.09.003 (2013).
Leja, K. et al. Hypothetical glycerol pathways of newly isolated strains capable of 1,3-propanediol production. Acta Biochim. Pol. 61, 759–763 (2014).
Emptage, M., Haynie, S. L., Laffend, L. A., Pucci, J. P. & Whited, G. Genetically engineered Escherichia coli containing nonspecific dehydratase yghD and dha regulon for the biological production of 1, 3-propanediol with high titer. US Patent patent (1997).
Celinska, E. Fully glycerol-independent microbial production of 1, 3-propanediol via non-natural pathway: Paving the way to success with synthetic tiles. Biotechnol. J., 10.1002/biot.201400360 (2014).
Chou, C. H., Chang, W. C., Chiu, C. M., Huang, C. C. & Huang, H. D. FMM: a web server for metabolic pathway reconstruction and comparative analysis. Nucleic Acids Res. 37, W129–134, 10.1093/nar/gkp264 (2009).
Kanehisa, M. et al. Data, information, knowledge and principle: back to metabolism in KEGG. Nucleic Acids Res. 42, D199–205, 10.1093/nar/gkt1076 (2014).
Hatzimanikatis, V. et al. Exploring the diversity of complex metabolic networks. Bioinformatics 21, 1603–1609, 10.1093/bioinformatics/bti213 (2005).
Barron, M. G., Lilavois, C. R. & Martin, T. M. MOAtox: A comprehensive mode of action and acute aquatic toxicity database for predictive model development. Aquat. Toxicol. 161C, 102–107, 10.1016/j.aquatox.2015.02.001 (2015).
Kimelman, A. et al. A vast collection of microbial genes that are toxic to bacteria. Genome Res. 22, 802–809, 10.1101/gr.133850.111 (2012).
MarvinSketch . Online Chemical Editor (MarvinSketch) - Draw Molecules and Reactions Online. (2015).
Aziz, R. K. et al. SEED servers: high-performance access to the SEED genomes, annotations and metabolic models. PloS One 7, e48053, 10.1371/journal.pone.0048053 (2012).
Haveren, J. V., Scott, E. L. & Sanders, J. Bulk chemicals from biomass. Biofuels, Bioprod. Biorefin. 2, 41–57 (2008).
Bennett, B. D. et al. Absolute metabolite concentrations and implied enzyme active site occupancy in Escherichia coli. Nat. Chem. Biol. 5, 593–599, 10.1038/nchembio.186 (2009).
Lewis, N. E. et al. Omic data from evolved E. coli are consistent with computed optimal growth from genome-scale models. Mol. Syst. Biol. 6, 390, 10.1038/msb.2010.47 (2010).
Lee, S., Phalakornkule, C., Domach, M. M. & Grossmann, I. E. Recursive MILP model for finding all the alternate optima in LP models for metabolic networks. Comput. Chem. Eng. 24, 711–716, 10.1016/S0098-1354(00)00323-9 (2000).
Ignizio, J. P. & Cavalier, T. M. Linear Programming. (Prentice-Hall, Inc. 1994).
Acknowledgements
The authors acknowledge the contributions of Akhil Kumar for the preparation of the metabolite and reaction sets from the MetRxn database and Hadi Nazeem Bokayee for his useful inputs during the preparation of the manuscript. The authors gratefully acknowledge funding from the DOE (http://www.energy.gov/) grant no. DE-SC0008091 and the NSF (http://www.nsf.gov/) award no. EEC-0813570. The funders had no role in the study design, data collection and analysis, decision to publish, or preparation of the manuscript.
Author information
Authors and Affiliations
Contributions
Conceived and designed experiments: C.D.M. and A.C. Performed the experiments: A.C. Analyzed the data: A.C. and C.D.M. Contributed reagents/materials/analysis tools: A.C. and C.D.M. Wrote paper: A.C. and C.D.M.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Chowdhury, A., Maranas, C. Designing overall stoichiometric conversions and intervening metabolic reactions. Sci Rep 5, 16009 (2015). https://doi.org/10.1038/srep16009
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep16009
This article is cited by
-
Calculation of All Possible Stoichiometric Coefficients and Theoretical Yields of Microbial Global Reactions
Biotechnology and Bioprocess Engineering (2022)
-
A metabolic reconstruction of Lactobacillus reuteri JCM 1112 and analysis of its potential as a cell factory
Microbial Cell Factories (2019)
-
Pareto Optimality Explanation of the Glycolytic Alternatives in Nature
Scientific Reports (2019)
-
Pathway design using de novo steps through uncharted biochemical spaces
Nature Communications (2018)
-
A review of parameters and heuristics for guiding metabolic pathfinding
Journal of Cheminformatics (2017)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.