Abstract
Iodine is an element of fascinating chemical complexity and numerous hypervalent iodine compounds reveal vital value of applications in organic synthesis. Investigation of the synthesis and application of new type of hypervalent iodine compound has extremely significant meaning. Here, the formation of CsIn (n > 1) compounds is predicted up to 200 GPa using an effective algorithm. The current results show that CsI3 with space group of Pm-3n is thermodynamically stable under high pressure. Hypervalence phenomenon of iodine atoms in Pm-3n CsI3 with endless linear chain type structure appears under high pressure, which is in sharp contrast to the conventional understanding. Our study further reveals that Pm-3n CsI3 is a metallic phase with several energy bands crossing Fermi-surface and the pressure creates a peculiar reverse electron donation from iodine to cesium. The electron-phonon coupling calculations have proposed superconductive potential of the metallic Pm-3n CsI3 at 10 GPa which is much lower than that of CsI (180 GPa). Our findings represent a significant step toward the understanding of the behavior of iodine compounds at extreme conditions.
Similar content being viewed by others
Introduction
Iodine compounds have always been the subject of extensive studies because of their significant properties such as conduction characteristic1,2, optical property3, catalytic performance4,5 and medical application6, etc. For instance, cesium iodide (CsI) is one of the simplest and most representative ionic solids and extensive theoretical and experimental studies have been carried out7,8,9,10,11,12,13,14,15. CsI exhibits variety of interesting phenomena such as pressure involved metallization and superconductivity under high pressure12,13,14. In addition, organic molecules bearing hypervalent iodine moieties have been transformed from laboratory curiosities to useful and routinely employed reagents in organic synthesis16,17,18,19,20,21. Comparing with the relatively and easily synthesized organic complexity, the synthesis of inorganic hypervalent iodine compounds with attractive properties and its corresponding structures have been a long-standing puzzle. For I3− ion, its linear geometric structure was determined for the first time in 1935 by Mooney, who carried out X-ray analysis on ammonium triiodide22. The I3− anion belongs to the type of compounds known as hypervalent, which violate the Lewis octet rule23. Due to the representative hypervalence property of I3− ion, it is of great consideration for further study of CsIn (n > 1) compounds to explore the possibility of forming hypervalent CsIn with interesting properties or structures. Previous experimental works show that crystal CsI3 and CsI4 can be synthesized at ambient pressure24,25,26,27. Subsequently, experimental XRD measurement proposed that the crystal information of CsI3 and CsI4 were orthorhombic Pmnb and monoclinic P21/a symmetry, respectively28,29,30. W. Zhang et al. did an excellent work for NaxCly system by combining theoretical predictions and diamond anvil cell experiments31. They reported that Na3Cl, Na2Cl, Na3Cl2, NaCl3 and NaCl7 are theoretically stable and have unusual bonding and electronic properties at high pressure31. Na-Cl and Cs-I system are clearly analogous as typical ionic solids and they may adopt the same structures. Currently, the synthesis or the full high-pressure structural information of CsIn are still far from being clear and established. These structural uncertainties have impeded in-depth understanding and further exploration of phenomena of CsIn might under compression.
Here, we present systematic structure searches to establish the thermodynamically stable structures of CsIn (n = 2 − 5) up to 200 GPa using the developed CALYPSO (Crystal structure AnaLYsis by Particle Swarm Optimization) method32,33,34,35, which has been successfully used in numerous predictions regarding compounds and structures over the past few years36,37,38,39,40,41,42,43,44,45,46. Our work shows that CsI3 has the simple Pmnb structure at ambient pressure and undergoes a complicated transition to high symmetric cubic Pm-3n phase at high pressure. The current Pm-3n phase of CsI3 is a metal phase and the pressures create a peculiar reverse electron donation from iodine to cesium. In addition, the iodine atoms of Pm-3n phase forming into several completely linear chains show an attractive hypervalence phenomenon, which cannot be simply explained by traditional three-center-four-electron (3c-4e) scheme47,48,49. This work presents significant concerning on the synthesis and the fundamental structural properties of the simplest and most representative polyiodide materials with implications for an entire family of similar materials.
Calculation Methods
To obtain stable structures for CsIn, we carried out a structural search using a global minimization of free energy surfaces based on the CALYPSO methodology32,33,34,35 and the first-principles calculations. The remarkable feature of this methodology is the capability of predicting the stable structure with only the knowledge of the chemical composition at given external conditions (for example, pressure). The underlying ab initio structural relaxations, electron localization function (ELF) and electronic band structure calculations were performed within the framework of density functional theory (DFT) as implemented using by VASP (Vienna ab initio simulation package) code50. The generalized gradient approximation (GGA) within the framework of Perdew–Burke–Ernzerhof (PBE)51 was used for the exchange-correlation functional. And the projector augmented wave method (PAW)52 has been adopted, with 5s25p66s1 and 5s25p5 treated as valence electrons for cesium and iodine, respectively. The cutoff energy for the expansion of the wavefunction into plane waves was set at 400 eV and fine Monkhorst–Pack (MP) k meshes of 0.025 Å−1 have been chosen to ensure that all the enthalpy calculations are well converged. The phonon calculations have been carried out by using a supercell approach as implemented in the Phonopy code53. This method uses the forces obtained by the Hellmann-Feynman theorem calculated from the optimized 3 × 3 × 3 supercell. The Bader’s quantum theory of atoms in molecules (QTAIM) analysis54 was used for charge calculation.
Electron-phonon coupling (EPC) calculations have been performed using the pseudo-potential plane-wave method and density-functional perturbation theory55,56 as implemented in the Quantum-ESPRESSO package57. EPC calculation has been performed on 4 × 4 × 4 MP q meshes in the first Brillouin zone with a kinetic energy cutoff of 60 Ry. 16 × 16 × 16 MP k meshes are chosen to ensure k-point sampling convergence with Gaussians of 0.025 Ry, which approximates the zero-width limit in this calculation.
Results and Discussions
The high-pressure synthesis and structural information of CsIn
Structural predictions for CsIn (n = 2 − 5) have been performed with CALYPSO methodology32,33,34,35 using simulation sizes with 1–4 formula per primitive cell under a series of pressure points (0, 50, 100, 150 and 200 GPa). The enthalpy of formation per atom is calculated using the following formula:

where ΔHf is the enthalpy of formation per atom and H is the calculated enthalpy per chemical unit for each compound.
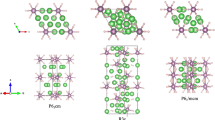
From the convex hull shown in Fig. 1a (solid lines), only CsI3 with space group of Pm-3n is thermodynamically stable under high pressure. However, previous experimental work shows that CsI4 can be synthesized at ambient pressure and a P21/a phase with 4 formulas per primitive cell has been proposed by X-ray analysis29. The currently predicted Pnma phase is energetically much superior to the monoclinic P21/a structure, while the formation enthalpy of Pnma is positive value and thus does not support its thermodynamic stability. We note that the experimentally synthesized CsI4 was heated in a closed vessel at 90 °C and was then cooled slowly to 25 °C29. Therefore, the P21/a CsI4 structure is a metastable phase. CsI3 is stable at ambient pressure and adopts an orthorhombic lattice with Pmnb symmetry (Fig. 2a). The optimized lattice parameter of Pmnb phase at 0 GPa is a = 7.2366 Å, b = 11.2631 Å and c = 10.4905 Å. At 0 GPa, this actually Cs+[I3]− phase contains linear type I3− ions with two I–I bonds length of 2.901 and 3.019 Å, which are similar to the experimental data of 2.820 and 3.100 Å28, respectively. Such typical hypervalent iodine moiety of orthorhombic Pmnb structure can be conventionally explained by traditional theory. For I3− ion of Pmnb phase, the central iodine atom shares two electrons with two adjacent iodine atoms by forming one 3c-4e bond and meanwhile it gets one electron from cesium atom to keep the other two iodine atoms following Lewis octet rule23. On the other hand, Pauling58 and Cartmell59 interpreted the hypervalence phenomenon of this ion in terms of the trigonal-bipyramidal orbitals of the central atom (sp3d hybridization). The central iodine atom has 10 electrons in valence shell which supports the conventional hypervalence phenomenon. The Pmnb structure remains stable up to 7.8 GPa, where undergoes a complicated first-order phase transition to cubic Pm-3n structure with volume collapse of 7.19% (Fig. 1b). The optimized lattice parameters of Pm-3n phase at 10 GPa is a = 6.2865 Å. Atoms occupy the Wyckoff 2a (0, 0, 0) for cesium and 6d (0, 0.5, 0.75) for iodine. Surprisingly, the enthalpies of Pm-3n phase at least up to 200 GPa from convex hull (Fig. 1a) show that Pm-3n phase tends to decompose as the increasing pressure.
Comparing with orthorhombic Pmnb structure, a striking feature of this modification is that all the iodine atoms form endless linear chains (Fig. 2b). And these endless chains just locate on the surface of the Pm-3m Cs lattice. The lattice dynamics calculations with no imaginary phonon frequencies support the dynamic stability of Pm-3n structure over the pressure range studied here (Fig. 3a). Remarkly, the endless chain structure has rarely been found in inorganic compounds before. One previous work shows that the B atoms of Li2B can form kinked chains along the c axis under high pressure38. However, such kinked chains of B is clearly different from iodine chains which are thoroughly linear without any tortuosity. The similar crystal structures with Pnma and Pm-3n space groups have been reported for NaCl331. NaCl3 is stable in the Pnma containing almost linear asymmetric Cl3 groups at 20 to 48 GPa and then transforms into a metallic Pm-3n structure. NaCl3 and CsI3 are clearly analogous compounds and even adopt the same structures and Cl-Cl bonds in Pm-3n NaCl3 similar with our predicted I-I bonds by forming extended monatomic chains running along the three mutually perpendicular axes31. In addition, the Cs–I bond length in CsI3 is close to that in CsI as pressures change, indicating the forming of Cs–I ionic bond (Fig. 3b). And the I–I bond length in CsI3 is 2.764 Å at 60 GPa, significantly shorter than the shortest I–I distances of 3.021 Å in solid I2 (Fig. 3b), showing a stronger bonding character. The ELF of CsI3 at 150 GPa shows that the strongest electron localization area are located between iodine and iodine atoms (Fig. 3c), suggesting covalent bond forms between the iodine atoms. As we well know, pressure-induced molecular dissociation of solid I2 has been reported from theoretical or experimental studies, but iodine in Pm-3n phase can held together by strong chemical bonds at least until 200 GPa. We have calculated the charges using Bader’s quantum theory of atoms in molecules (QTAIM) analysis54 for CsI3 at high pressure. From Fig. 3d, the electrons devoted from cesium to iodine are gradually reduced as the increasing pressure, indicating a peculiar reverse electron donation from iodine to cesium and thus naturally gives rise to suppress the strength of Cs–I bonds, which is responsible for tendency of the decomposition at higher pressure. Each iodine atom of CsI3 gets two shared electrons from the nearest-neighbor iodine and averagely 0.3 electrons from cesium atom and frankly the valence shell of iodine has 9.3 electrons with hypervalence character. Generally, several hypervalent compounds such as hypervalent P, S, I and Xe in PCl5, SF6, IF7 and XeF4 always have integral electrons in valence shell of 10, 12, 14 and 12, respectively60. For conventional hypervalent iodine compounds, only one central atom possesses hypervalence property which being surrounded by other several ligands. While in the current ionic CsI3 compound, all the iodine atoms possess such character, which broadens conventional understanding of hypervalent iodine. Therefore, high pressure induces the attractive hypervalent phenomenon in CsI3 iodine with specific endless linear chain structure.
The lattice dynamics and bonding behavior analysis of Pm-3n CsI3.
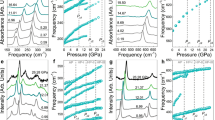
(a) Calculated phonon spectrum of Pm-3n CsI3 at 10 GPa. (b) Interatomic distances (between atoms shown in the structure directly underneath) in I2, CsI3 and CsI as a function of external pressure. (c) ELF of CsI3 at 150 GPa. (d) Calculated Bader charge of cesium and iodine in CsI3 as a function of external pressure.
At ambient pressure, the prototypical ionic crystal of CsI3 is an insulator. Interestingly, CsI3 becomes metallic after the first-order phase transition at 7.8 GPa. The calculated electronic band structures of Pm-3n phase at 10 GPa show it is metallic with several bands crossing Fermi level (Fig. 4a). Pressure induces CsI3 to exhibit increasingly shorter interatomic distances, which is accompanied by an increase in the bandwidth, especially those near the Fermi-surface, thus leading to the 5p bands of iodine expand along conductive band direction (Fig. 4b). Furthermore, the calculated projected density of states (PDOS) of CsI3 show that the 5d states of Cs have more electronic occupation as the pressure increasing (Fig. 4c,d).
It should be mentioned that the superconducting behaviors in CsI have been extensively explored through experimental measurement and theoretical calculations12,13,14. It is suggested that the formation of several electrons and hole Fermi-surface pockets in CsI is due to a dramatic increase of the electron donation from I− to Cs+, thus leading to more electrons to be involved in the electron-phonon coupling which is responsible for superconductivity and the larger EPC potential, thereby contributing to the increase in TC12. Therefore, it is intriguing to determine whether Pm-3n CsI3 will possess superconducting property under high pressure.
Figure 5 shows the phonon density of states (PHDOS) and Eliashberg spectral function α2F (ω)61 for Pm-3n CsI3 at 10 GPa. It is found that α2F (ω) contains two parts of which the low and high frequency area are localized within a narrow vibrational region of 0.8–3.4 THz and 3.4–4.2 THz, respectively. The integrated EPC λ of low frequency α2F (ω) are 0.353 constituting 95.66% of the total λ 0.369 and the other EPC λ in high frequency area is 0.016 accounts 4.34% of total λ. With increasing pressure to 150 GPa, λ was reduced to be 0.074. The superconducting critical temperature TC can be estimated from the Allen-Dynes modified McMillan equation62  , where ωlog is the logarithmic average frequency calculated directly from the phonon spectrum and μ* is the Coulomb pseudopotential. ωlog is obtained to be 97.33 K at 10 GPa and 322.96 K at 150 GPa. Using a μ* of 0.1, the estimated TC is 0.15 K at 10 GPa but it disappears at 150 GPa. It is noteworthy that the estimated TC in CsI3 is noticeably larger than the value in CsI of 0.03 K and the pressure is significantly lower than that of CsI (180 GPa).
, where ωlog is the logarithmic average frequency calculated directly from the phonon spectrum and μ* is the Coulomb pseudopotential. ωlog is obtained to be 97.33 K at 10 GPa and 322.96 K at 150 GPa. Using a μ* of 0.1, the estimated TC is 0.15 K at 10 GPa but it disappears at 150 GPa. It is noteworthy that the estimated TC in CsI3 is noticeably larger than the value in CsI of 0.03 K and the pressure is significantly lower than that of CsI (180 GPa).
Conclusions
In summary, we have systematically investigated compounds CsIn up to 200 GPa using an effective CALYPSO algorithm. Strikingly, CsI3 with space group of Pm-3n is thermodynamic stability under high pressure. Within the cubic Pm-3n CsI3 phase, iodine atoms arranging into several endless linear chains show an attractive hypervalence phenomenon under high pressure, which is in sharp contrast to the conventional understanding. We further discovered that Pm-3n CsI3 is a metallic phase with several energy bands crossing Fermi-surface and the pressure creates a peculiar reverse electron donation from iodine to cesium. The electron-phonon coupling calculations have proposed superconductive potential of the metallic Pm-3n CsI3 at 10 GPa, which are analogous to the known CsI12. This work has wide implications for other inorganic compounds that likely harbor similar high-pressure behavior and the significance for synthetic chemistry is highlighted.
Additional Information
How to cite this article: Wei, S. et al. Hypervalent Iodine with Linear Chain at High Pressure. Sci. Rep. 5, 14393; doi: 10.1038/srep14393 (2015).
References
Liang, C. C. Conduction Characteristics of the Lithium Iodide-Aluminum Oxide Solid Electrolytes. J. Electrochem. Soc. 120, 1289–1292 (1973).
Bradley, J. N. & Greene, P. D. Potassium iodide+silver iodide phase diagram. High ionic conductivity of KAg4I5 . Trans. Faraday. Soc. 62, 2069–2075 (1966).
Yuster, P. H. & Delbecq, C. J. Some Optical Properties of Potassium Iodide-Thallium Phosphors. J. Chem. Phys. 21, 892–898 (1953).
Xie, W. & Li, H. Alumina-supported potassium iodide as a heterogeneous catalyst for biodiesel production from soybean oil. J. Mol. Catal. A: Chem. 255, 1–9 (2006).
Prajapati, D. & Sandhu, J. S. Cadmium iodide as a new catalyst for knoevenagel condensations. J. Chem. Soc. Perkin Trans. 1, 739–740 (1993).
Smanik, P. A. et al. Cloning of the human sodium iodide symporter. Biophys. Res. Commun. 226, 339–345 (1996).
Mao, H. K., Hemley, R. J., Chen, L. C., Shu, J. F. & Finger, L. W. X-ray diffraction to 302 gigapascals: High-pressure crystal structure of cesium iodide. Science 246, 649 (1989).
Eremets, M. I., Shimizu, K., Kobayashi, T. C. & Amaya, K. Metallic CsI at pressures of up to 220 gigapascals. Science 281, 1333 (1998).
Hemley, R. J. Superconductivity in a Grain of Salt. Science 281, 1296 (1998).
Huang, T. L. & Ruoff, A. L. Equation of state and high-pressure phase transition of CsI. Phys. Rev. B 29, 1112 (1984).
Mao, H. K. et al. High-pressure phase transition and equation of state of CsI. Phys. Rev. Lett. 64, 1749 (1990).
Xu, Y. et al. Superconducting high-pressure phase of cesium iodide. Phys. Rev. B 79, 144110 (2009).
Eremets, M. I., Shimizu, K., Kobayashi, T. C. & Amaya, K. Metallic CsI at pressures of up to 220 gigapascals. Science 281, 1333 (1998).
Eremets, M. I., Shimizu, K., Kobayashi, T. C. & Amaya, K. Metallization and superconductivity in CsI at pressures up to 220 GPa. J. Phys. Condens. Matter 10, 11519 (1998).
Zhang, F., Gale, J. D., Uberuaga, B. P., Stanek, C. R. & Marks, N. A. Importance of dispersion in density functional calculations of cesium chloride and its related halides. Phys. Rev. B 88, 054112 (2013).
De Mico, A., Margarita, R., Parlanti, L., Vescovi, A. & Piancatelli, G. A versatile and highly selective hypervalent iodine (III)/2, 2, 6, 6-tetramethyl-1-piperidinyloxyl-mediated oxidation of alcohols to carbonyl compounds. J. Org. Chem. 62, 6974–6977 (1997).
Wirth, T. Hypervalent iodine chemistry in synthesis: scope and new directions. Angew. Chem.-Int. Edit. 44, 3656–3665 (2005).
Frigerio, M., Santagostino, M., Sputore, S. & Palmisano, G. Oxidation of Alcohols with o-Iodoxybenzoic Acid in DMSO: A New Insight into an Old Hypervalent Iodine Reagent. J. Org. Chem. 60, 7272–7276 (1995).
Moriarty, R. M. & Vaid, R. K. Carbon-carbon bond formation via hypervalent iodine oxidations. Synthesis 6, 431–447 (1990).
Richardson, R. D. & Wirth, T. Hypervalent iodine goes catalytic. Angew. Chem.-Int. Edit. 45, 4402–4404 (2006).
Tohma, H., Takizawa, S., Maegawa, T. & Kita, Y. Facile and clean oxidation of alcohols in water using hypervalent iodine (III) reagents. Angew. Chem.-Int. Edit. 39, 1306–1308 (2000).
Mooney, R. C. L. The Configuration of the Triiodide Group in Ammonium Triiodide Crystals. Z. Krist. 90, 143 (1935).
Lewis, G. N. The atom and the molecule. J. Am. Chem. Soc. 38, 762 (1916).
Bozorth, R. M. & Pauling, L. The crystal structures of cesium Tri-Iodide and cesium Dibromo-Iodide. J. Am. Chem. Soc. 47, 1561–1571 (1925).
Briggs, T. R. The Polyiodides of Cesium. II. J. Phys. Chem. 34, 2260 (1930).
Briggs, T. R., Greenawald, J. A. & Leonard, J. W. The Polyiodides of Cesium–Cesium Iodide, Iodine and Water at 25°. J. Phys. Chem. 34, 1951–1960 (1930).
Briggs, T. R., Clack, K. D. G., Ballard, K. H. & Sassaman, W. A. Polyiodides of Potassium. II. The Ternary System Potassium Iodide–Iodine–Water. J. Phys. Chem. 44, 350–372 (1940).
Tasman, H. A. & Boswijk, K. H. Re-investigation of the crystal structure of CsI3 . Acta Cryst. 8, 59–60 (1955).
Havinga, E. E., Boswijk, K. H. & Wiebenga, E. H. The crystal structure of Cs2I8 (CsI4). Acta Cryst. 7, 487–490 (1954).
Breneman, G. L. & Willett, R. D. The crystal structure of cesium tribromide and a comparison of the Br3− and I3− systems. Acta Cryst. B 25, 1073–1076 (1969).
Zhang, W. et al. Unexpected Stable Stoichiometries of Sodium Chlorides. Science 342, 1502–1505 (2013).
Wang, Y., Lv, J., Zhu, L. & Ma, Y. CALYPSO: A method for crystal structure prediction. Comput. Phys. Commun. 183, 2063–2070 (2012). CALYPSO Code is Free for Academic Use. Please Register athttp://www.calypso.cn.
Wang, Y., Lv, J., Zhu, L. & Ma, Y. Crystal structure prediction via particle-swarm optimization. Phys. Rev. B 82, 094116 (2010).
Wang, Y. et al. An effective structure prediction method for layered materials based on 2D particle swarm optimization algorithm. J. Chem. phys. 137, 224108 (2012).
Lv, J., Wang, Y., Zhu, L., & Ma, Y. Particle-swarm structure prediction on clusters. J. Chem. Phys. 137, 084104 (2012).
Zhang, M. et al. Superhard BC3 in Cubic Diamond Structure. Phys. Rev. Lett. 114, 015502 (2015).
Zhou, D., Li, Q., Ma, Y., Cui, Q. & Chen, C. Unraveling convoluted structural transitions in SnTe at high pressure. J. Phys. Chem. C 117, 5352 (2013).
Peng, F., Miao, M., Wang, H., Li, Q. & Ma, Y. Predicted lithium–boron compounds under high pressure. J. Am. Chem. Soc. 134, 18599 (2012).
Wang, H., John, S. T., Tanaka, K., Iitaka, T. & Ma, Y. Superconductive sodalite-like clathrate calcium hydride at high pressures. Proc. Natl. Acad. Sci. USA 109, 6463 (2012).
Zhu, L. et al. Spiral chain O4 form of dense oxygen. Proc. Natl. Acad. Sci. USA 109, 751 (2012).
Li, Q., Zhou, D., Zheng, W., Ma, Y. & Chen, C. Global structural optimization of tungsten borides. Phys. Rev. Lett. 110, 136403 (2013).
Lu, C., Miao, M. & Ma, Y. Structural Evolution of Carbon Dioxide under High Pressure. J. Am. Chem. Soc. 135, 14167 (2013).
Li, Q. et al. A novel low compressible and superhard carbon nitride: Body-centered tetragonal CN2 . Phys. Chem. Chem. Phys. 14, 13081 (2012).
Lu, S., Wang, Y., Liu, H., Miao, M. S. & Ma, Y. Self-assembled ultrathin nanotubes on diamond (100) surface. Nature Commun. 5, 3666 (2014).
Zhu, L., Liu, H., Pickard, C. J., Zou, G. & Ma, Y. Reactions of xenon with iron and nickel are predicted in the Earth’s inner core. Nature Chem. 6, 644–648 (2014).
Wei, S. et al. High-pressure phase transition of cesium chloride and cesium bromide. Phys. Chem. Chem. Phys. 16, 17924–17929 (2014).
Hach, R. J. & Rundle, R. E. The Structure of Tetramethylammonium Pentaiodide1, 1a. J. Am. Chem. Soc. 73, 4321 (1951).
Rundle, R. E. On the Problem Structure of XeF4 and XeF2 . J. Am. Chem. Soc. 85, 112 (1963).
Pimentel, G. C. The bonding of trihalide and bifluoride ions by the molecular orbital method. J. Chem. Phys. 19, 446 (1951).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169 (1996).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865 (1996).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953–17979 (1994).
Togo, A., Oba, F. & Tanaka, I. First-principles calculations of the ferroelastic transition between rutile-type and CaCl2-type SiO2 at high pressures. Phys. Rev. B 78, 134106 (2008).
Bader, R. F. W. Atoms in Molecules: A Quantum Theory, Oxford Univ. Press, (1990).
Baroni, S., Giannozzi, P. & Testa, A. Green’s-function approach to linear response in solids. Phys. Rev. Lett. 58, 1861 (1987).
Giannozzi, P., De Gironcoli, S., Pavone, P. & Baroni, S. Ab initio calculation of phonon dispersions in semiconductors. Phys. Rev. B 43, 7231 (1991).
Giannozzi, P. et al. QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 21, 395502 (2009).
Pauling, L. The Nature of the Chemical Bond, 2nd ed. Cornell Univ. Press, Ithaca, NY, p111 (1948).
Cartmell, E. & Fowles, G. W. A. Valency and Molecular Structure. Butterworth and Co. Ltd., London, p177 (1956).
Musher, J. I. The chemistry of hypervalent molecules. Angew. Chem. Int. Ed. Engl. 8, 54–68 (1969).
Allen, P. B. Neutron spectroscopy of superconductors. Phys. Rev. B 6, 2577 (1972).
Allen, P. B. & Dynes, R. C. Transition temperature of strong-coupled superconductors reanalyzed. Phys. Rev. B 12, 905 (1975).
Acknowledgements
This work is supported by the China 973 Program (2011CB808200), the Natural Science Foundation of China under 51202084, 11474125 and 11274136, the 2012 Changjiang Scholars Program of China, Changjiang Scholar and Innovative Research Team in University (IRT1132), Project 2015129 Supported by Graduate Innovation Fund of Jilin University. Parts of the calculations were performed in the High Performance Computing Center (HPCC) of Jilin University.
Author information
Authors and Affiliations
Contributions
Q.L. conceived and provided critical ideas for the work. S.W. performed most of the calculations. S.W., J.W., S.D. and S.Z. analysed the data. J.W. carried out the phonon calculations. All authors commented on the manuscript. S.W. and Q.L. wrote the paper.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Wei, S., Wang, J., Deng, S. et al. Hypervalent Iodine with Linear Chain at High Pressure. Sci Rep 5, 14393 (2015). https://doi.org/10.1038/srep14393
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep14393
This article is cited by
-
Modern level for properties prediction of iodine-containing organic compounds: the halogen bonds formed by iodine
Russian Chemical Bulletin (2017)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.