Abstract
Topological insulators (TIs) are interesting quantum matters that have a narrow bandgap for bulk and a Dirac-cone-like conducting surface state (SS). The recent discovered second Dirac surface state (SS) and bulk bands (BBs) located ~1.5 eV above the first SS are important for optical coupling in TIs. Here, we report on the time-domain measurements of THz radiation generated from TIs n-type Cu0.02Bi2Se3 and p-type Bi2Te3 single crystals by ultrafast optical pulse excitation. The observed polarity-reversal of the THz pulse originated from transient current is unusual and cannot be reconciled with the photo-Dember effect. The second SS and BBs are found to be indispensable for the explanation of the unusual phenomenon. Thanks to the existence of the second SS and BBs, TIs manifest an effective wide band gap in THz generation. The present study demonstrates that time-domain THz spectroscopy provide rich information of the optical coupling and the electronic structure of TIs.
Similar content being viewed by others
Introduction
A new phase of quantum matters called topological insulators (TIs) are theoretically predicted and experimentally observed recently and their band structures are composed of insulating bulk bands and a conducting surface state (SS). The SS results from a strong spin-orbital interaction and band inversion1,2 and exhibits novel properties, such as the protection by time-reversal symmetry against backscattering from nonmagnetic impurities3,4,5 and spin-polarized current6,7,8. These properties hint at potential applications in spintronic devices and quantum computations. Dirac fermions in TIs have been extensively studied using angle-resolved photoemission spectroscopy (ARPES)9,10,11 or scanning tunneling microscopy (STM)12,13,14,15. Optical techniques, such as surface second harmonics generation (SHG), have provided an alternative contact-free detection for Dirac Fermion16,17 and ultrafast optical techniques also have been used to study the characteristics of TIs18,19,20,21,22. Very recently, an unoccupied 2nd SS and bulk bands (BBs) which are located above the 1st SS were predicted23 and observed in the material family of Bi2TexSe3-x using ARPES and two-photon photoemission measurements24,25. The 2nd SS also originates from the strong spin-orbital coupling and is expected to keep the same topological and spin characteristics as the 1st SS23,24. However, the role of the 2nd SS and BBs on the interactions between TIs and photons has been much less investigated. Further explorations on the relevant subjects are indispensable to the development of TI optical devices.
This study reports the time domain measurements of THz radiation generated from the surface and bulk of n-type Cu0.02Bi2Se3 and p-type Bi2Te3 single crystals. Two different mechanisms of THz generation: optical rectification (OR) and transient current, have been identified by different polarization configurations of both optical excitation and THz radiation. With this time-domain technique, the 2nd SS and BBs manifest themselves in the spectrum and prove vital in generating the THz radiation through a transient drift current.
Results
P-polarized THz radiation from TIs
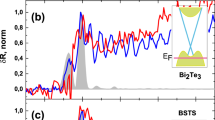
The experimental setup was a reflective type, where the optical pulse illuminated the (111) surfaces of the TI crystals at an incident angle of 45°, to generate THz radiation, as shown in Fig. 1(a). Two types of TI single crystals were used in this study: Cu-doped n-type Bi2Se3 (Cu0.02Bi2Se3) with a carrier concentration of 3.66 × 1018 cm−3 and p-type Bi2Te3 with a carrier concentration of 1.32 × 1019 cm−3. Both were determined using the Hall measurements and the ARPES images of the employed single crystals are shown in Fig. 1(b,c). Figure 2(a,b) show the typical time domain THz waveforms with several cycles for the n-type TIs. In these two cases, the P- and S-polarized optical pulse illuminated the surface of an n-type Cu0.02Bi2Se3 single crystal and a wire-grid polarizer was set to detect P-polarized THz waves (denoted by POpt-PTHz and SOpt-PTHz), respectively. Figure 2(e) shows the dependence of the azimuthal angle ( -scan) of the peak-to-peak value of the THz pulse (ATHz) from the (111) surface of Cu0.02Bi2Se3 in POpt-PTHz configuration and a corresponding x-ray diffraction (XRD)
-scan) of the peak-to-peak value of the THz pulse (ATHz) from the (111) surface of Cu0.02Bi2Se3 in POpt-PTHz configuration and a corresponding x-ray diffraction (XRD)  -scan of the (1 1 15) peak of TI crystals. The result in SOpt-PTHz configuration is shown in Fig. 2(f). In these two configurations, the
-scan of the (1 1 15) peak of TI crystals. The result in SOpt-PTHz configuration is shown in Fig. 2(f). In these two configurations, the  -dependent THz peak-to-peak value (THz
-dependent THz peak-to-peak value (THz  -scan) does not show a significant three-fold symmetry associated with that of the crystalline structure of Cu0.02Bi2Se3. Because the P-polarized THz radiation contains both in-plane and out-of-plane electric-field components, the THz
-scan) does not show a significant three-fold symmetry associated with that of the crystalline structure of Cu0.02Bi2Se3. Because the P-polarized THz radiation contains both in-plane and out-of-plane electric-field components, the THz  -scan results show that the P-polarized THz radiation is dominated by the out-of-plane component from the bulk of the TIs, as shown in Fig. 1(a). Obviously, the THz waveforms from Cu0.02Bi2Se3 are similar to that from InAs (thin-red line in Fig. 2(a)) but the amplitude of the P-polarized THz pulse from Cu0.02Bi2Se3 is much smaller than that from InAs under the same conditions.
-scan results show that the P-polarized THz radiation is dominated by the out-of-plane component from the bulk of the TIs, as shown in Fig. 1(a). Obviously, the THz waveforms from Cu0.02Bi2Se3 are similar to that from InAs (thin-red line in Fig. 2(a)) but the amplitude of the P-polarized THz pulse from Cu0.02Bi2Se3 is much smaller than that from InAs under the same conditions.
(a–d) Time-domain P-polarized THz waveforms radiated from the (111) surface of n-type Cu0.02Bi2Se3 and p-type Bi2Te3 by P- and S-polarized optical pulse excitation. In (a), the thin-red line represents the 0.015-times smaller P-polarized THz wave that is generated from an n-type InAs under the same conditions. In both POpt-PTHz and SOpt-PTHz configurations, the polarities of the P-polarized THz waveforms from p-type Bi2Te3 (c,d) are in the reverse of that from n-type Cu0.02Bi2Se3 (a,b). ATHz is the peak-to-peak value of the THz waveform. (e–h): the plots of ATHz for the P-polarized THz waveforms as a function of azimuthal angles ( -scan) of Cu0.02Bi2Se3 (a,b) and Bi2Te3 (c,d) single crystals (black). The corresponding XRD
-scan) of Cu0.02Bi2Se3 (a,b) and Bi2Te3 (c,d) single crystals (black). The corresponding XRD  -scans for the (1 1 15) peak for both single crystals are also shown in (e–h) (green).
-scans for the (1 1 15) peak for both single crystals are also shown in (e–h) (green).
Figure 2(c,d) show the typical time-domain THz waveforms from a p-type Bi2Te3 single crystal in the configurations of POpt-PTHz and SOpt-PTHz, respectively. The shape and amplitude are almost the same as those for the n-type Cu0.02Bi2Se3 in Fig. 2(a,b). The THz  -scans in Fig. 2(g,h) do not show a significant three-fold symmetry associated with the crystalline structure of Bi2Te3, either. Nevertheless, the polarities of the P-polarized THz pulse from p-type Bi2Te3 are opposite to those from the n-type Cu0.02Bi2Se3. This intriguing contrast provides a revealing insight into TIs’ optical coupling and novel electronic structure as we shall show later.
-scans in Fig. 2(g,h) do not show a significant three-fold symmetry associated with the crystalline structure of Bi2Te3, either. Nevertheless, the polarities of the P-polarized THz pulse from p-type Bi2Te3 are opposite to those from the n-type Cu0.02Bi2Se3. This intriguing contrast provides a revealing insight into TIs’ optical coupling and novel electronic structure as we shall show later.
S-polarized THz radiation from TIs
In the experiments of the POpt-PTHz and SOpt-PTHz configurations, the in-plane contribution to THz radiation cannot be separated. To obtain the in-plane contribution to THz radiation, the wire-grid polarizer and the EO sampling setup were rotated to detect the S-polarized THz radiation under P- and S-polarized optical excitation (POpt-STHz and SOpt-STHz). Figure 3(a) shows the time-domain THz waveforms from the (111) surface of n-type Cu0.02Bi2Se3 in the POpt-STHz configuration. The results in SOpt-STHz configuration is also shown in Fig. 3(b). Although the signal-to-noise ratio is low (about 2 to 3), it still can be observed that the polarity of the THz waveform is reversed if the azimuth angle of samples is rotated by 180°. The similar results of p-type Bi2Te3 are shown in Fig. 3(c,d). The origins of S-polarized THz radiation shall be discussed later.
(a–d) Time-domain S-polarized THz waveforms radiated from the (111) surface of n-type Cu0.02Bi2Se3 and p-type Bi2Te3 by P- and S-polarized optical pulse excitation. In all polarization configurations, the polarities of S-polarized THz waveforms are reversed when the samples are rotated 180° along the surface normal. ATHz is the peak-to-peak value of the THz waveform. (e–h): the plots of ATHz for the S-polarized THz waveforms as a function of azimuthal angles ( -scan) of Cu0.02Bi2Se3 (a,b) and Bi2Te3 (c,d) single crystals (black). Obviously, the THz
-scan) of Cu0.02Bi2Se3 (a,b) and Bi2Te3 (c,d) single crystals (black). Obviously, the THz  -scans for both single crystals match the XRD
-scans for both single crystals match the XRD  -scans for the (1 1 15) peak (green).
-scans for the (1 1 15) peak (green).
Discussion
For THz generation from common semiconductors, there are three possible mechanisms: (1) optical rectification (OR), (2) the photo-Dember effect and (3) the surface field effect26. In the experimental results, the P-polarized THz radiation from both Cu0.02Bi2Se3 and Bi2Te3 do not show a significant three-fold symmetry that is related to the crystalline structure and this excludes OR as the mechanism for P-polarized THz radiation from TIs. However, both the photo-Dember effect and the surface field effect are associated with transient current from photocarriers that are excited by an optical pump pulse inside the material. The far-field electrical field  for THz radiation is described by
for THz radiation is described by

where  is the transient current created by an optical pulse and it is composed of diffusion current
is the transient current created by an optical pulse and it is composed of diffusion current  and drift current
and drift current  . The amplitude of
. The amplitude of  is proportional to the time-derivative of
is proportional to the time-derivative of  . In general, the direction of
. In general, the direction of  is normal to the surface of the material and it contributes to the P-polarized THz radiation if the pump beam is obliquely incident. The polarity of the THz radiation also depends on the direction of
is normal to the surface of the material and it contributes to the P-polarized THz radiation if the pump beam is obliquely incident. The polarity of the THz radiation also depends on the direction of  , whether it is inward to or outward from the surface of the material. The photo-Dember effect is a result of the concentration gradient of the photoexcited carriers near the semiconductor surface. Because there is a large difference between photoexcited electrons and holes in the diffusion coefficient and the mobility, photoexcited electrons in the bulk of a material diffuse much faster than holes, which causes the diffusion current
, whether it is inward to or outward from the surface of the material. The photo-Dember effect is a result of the concentration gradient of the photoexcited carriers near the semiconductor surface. Because there is a large difference between photoexcited electrons and holes in the diffusion coefficient and the mobility, photoexcited electrons in the bulk of a material diffuse much faster than holes, which causes the diffusion current  to be the main component of
to be the main component of  in Eq. (1). Therefore, the photo-Dember effect is the dominant mechanism for THz generation from narrow bandgap semiconductors26, such as InAs (bandgap ∼ 0.36 eV) and InSb (bandgap ∼ 0.17 eV). In this case, the direction of
in Eq. (1). Therefore, the photo-Dember effect is the dominant mechanism for THz generation from narrow bandgap semiconductors26, such as InAs (bandgap ∼ 0.36 eV) and InSb (bandgap ∼ 0.17 eV). In this case, the direction of  is always outward from the surface and the polarity of the THz pulses must be the same for both n- and p-type semiconductors. Although both n-type Cu0.02Bi2Se3 (bandgap ∼ 0.3 eV) and p-type Bi2Te3 (bandgap ∼ 0.15 eV) could be classified as narrow bandgap semiconductors, the photo-Dember effect cannot explain the reversed polarity of P-polarized THz radiation between n- and p-type TIs.
is always outward from the surface and the polarity of the THz pulses must be the same for both n- and p-type semiconductors. Although both n-type Cu0.02Bi2Se3 (bandgap ∼ 0.3 eV) and p-type Bi2Te3 (bandgap ∼ 0.15 eV) could be classified as narrow bandgap semiconductors, the photo-Dember effect cannot explain the reversed polarity of P-polarized THz radiation between n- and p-type TIs.
For wide bandgap semiconductors, such as GaAs (bandgap ∼ 1.43 eV), THz radiation can be explained by the surface field effect which is due to the acceleration of photoexcited carriers by the surface field near the semiconductor surface. The surface field is caused by band-bending due to Fermi-level pinning by the surface state26. The photoexcited electrons and holes are accelerated in opposite directions by the surface field to form a transient drift current  . In general, the direction of the surface field in n-type semiconductors is opposite to that in p-type semiconductors. Therefore, the directions of the induced transient currents are opposite and the polarity of THz pulses from n-type semiconductors is also opposite to that from p-type semiconductors.
. In general, the direction of the surface field in n-type semiconductors is opposite to that in p-type semiconductors. Therefore, the directions of the induced transient currents are opposite and the polarity of THz pulses from n-type semiconductors is also opposite to that from p-type semiconductors.
For Bi2Se3 and Bi2Te3, surface band-bending has been observed by previous studies, using angle-resolved photoemission spectroscopy, scanning tunneling spectroscopy and hard x-ray photoelectron spectroscopy27,28,29,30. Theoretical calculations also predict that the sign of band-bending could be affected by the type of doping: electron doping or hole doping31. Therefore, the polarity of P-polarized THz radiation from TIs is affected by the TIs’ doping. The experimental results indicate that  predominates over the photoexcited current inside p-type Bi2Te3, which further implies that the excess energy of the photoexcited carrier is too low to form a sufficiently strong photo-Dember field. However, from an energy point of view, the excess energy that the photoexcited carriers gain from the pumping photon energy is larger than that given by the surface field for narrow band semiconductors as in TIs. In this regard,
predominates over the photoexcited current inside p-type Bi2Te3, which further implies that the excess energy of the photoexcited carrier is too low to form a sufficiently strong photo-Dember field. However, from an energy point of view, the excess energy that the photoexcited carriers gain from the pumping photon energy is larger than that given by the surface field for narrow band semiconductors as in TIs. In this regard,  from the photo-Dember field should have been the dominant component of the photoexcited current32. This paradox can be beautifully resolved in the context of the 2nd SS and BBs in TIs. Very recently, using two-photon photoemission in ARPES measurements24,25, an unoccupied 2nd SS and BBs located 1.1 to 1.5 eV above the 1st SS were observed in the material family of Bi2TexSe3-x. For Bi2Se3, the energy difference between the 2nd band (2nd SS and BBs) and 1st band (1st SS, bulk conduction band: BCB and bulk valance band: BVB) matches the photon energy of 1.55 eV. It has also been confirmed that direct transitions to the 2nd SS and BBs can be driven by 1.55 eV optical pulses in n-type samples25. This indicates the excess energy of the photoexcited carriers would be reduced dramatically. For Bi2Te3, the 2nd SS is closer to the 1st SS24 than that of Bi2Se3. For the p-type Bi2Te3 samples, however, the energy difference between the 2nd band (2nd SS and BBs) and the 1st band (1st SS, BCB and BVB) would still lead to sufficient energy loss of the photoexcited carriers. As shown in Fig. 4, to have a brief summary, thanks to the existence of 2nd SS and BBs, TIs manifest an effective wide band gap in THz generation. The 2nd SS and BBs could result in energy loss for these photoexcited carriers that generate THz radiation in TIs. Therefore,
from the photo-Dember field should have been the dominant component of the photoexcited current32. This paradox can be beautifully resolved in the context of the 2nd SS and BBs in TIs. Very recently, using two-photon photoemission in ARPES measurements24,25, an unoccupied 2nd SS and BBs located 1.1 to 1.5 eV above the 1st SS were observed in the material family of Bi2TexSe3-x. For Bi2Se3, the energy difference between the 2nd band (2nd SS and BBs) and 1st band (1st SS, bulk conduction band: BCB and bulk valance band: BVB) matches the photon energy of 1.55 eV. It has also been confirmed that direct transitions to the 2nd SS and BBs can be driven by 1.55 eV optical pulses in n-type samples25. This indicates the excess energy of the photoexcited carriers would be reduced dramatically. For Bi2Te3, the 2nd SS is closer to the 1st SS24 than that of Bi2Se3. For the p-type Bi2Te3 samples, however, the energy difference between the 2nd band (2nd SS and BBs) and the 1st band (1st SS, BCB and BVB) would still lead to sufficient energy loss of the photoexcited carriers. As shown in Fig. 4, to have a brief summary, thanks to the existence of 2nd SS and BBs, TIs manifest an effective wide band gap in THz generation. The 2nd SS and BBs could result in energy loss for these photoexcited carriers that generate THz radiation in TIs. Therefore,  , rather than
, rather than  , may predominate over the photoexcited current in TIs and produce THz pulses with opposite polarity, due to the doping dependent band-bending.
, may predominate over the photoexcited current in TIs and produce THz pulses with opposite polarity, due to the doping dependent band-bending.
Schematic for the influence of the 2nd surface state (SS) and bulk bands (BBs) on the P-polarized THz generation from p-type Bi2Te3.
BCB: bulk conduction band. BVB: bulk valance band. The 2nd SS and BBs would be responsible for the energy loss of the photoexcited electrons. Thus, the surface field  induced by band-bending also results in the drift current
induced by band-bending also results in the drift current  in the narrow bandgap materials.
in the narrow bandgap materials.
The band-to-band transitions may contribute to the absorption of pumping photon to cause the reduction of energy. In general, this phenomenon can be described by the Fermi Golden rule, which is a way to calculate the transition probability between the initial and final density of states. This indicates that the band-to-band transitions could be further predicted by the statuses of initial and final density of states. For both cases of n-type Cu0.02Bi2Se3 and p-type Bi2Te3, the Fermi surface locates in the 1st band and no carriers fill the 2nd band and higher energy bands. While the samples were pumped by a femtosecond laser pulse with photon energy of 1.55 eV, the transition would predominantly occur between the 1st and 2nd band at the initial stage according to the Fermi Golden rule. Even there are some photoexcited carriers on 2nd band after pumping, the band-to-band transitions from the 2nd band and higher energy bands can be neglected due to the femtosecond ultrashort pulse (<75 fs), which doesn’t provide enough time for the further absorption of photoexcited carriers on the 2nd band or higher energy bands. On the other hand, if we use a long pulse for pumping, the band-to-band transitions should be considered for the THz generation on TIs.
In the cases of S-polarized THz radiation from TIs, as shown in Fig. 3(a,b), although the signal-to-noise ratio of the measured THz waveforms is low (about 2 to 3), it still can be observed that the polarity of the THz waveform is reversed if the azimuth angle of samples is rotated by 180°. Further, the THz  -scans in Fig. 3(e,f) also show a three-fold symmetry, which is consistent with the surface crystalline structure of Cu0.02Bi2Se3. A similar symmetry was also recently observed in SHG signal using ultrafast optical pulse illumination in Bi2Se316,17. For p-type Bi2Te3, the same phenomena are also observed, as shown in Fig. 3(c,d,g,h). Consequently, it is concluded that the OR is the main mechanism for S-polarized THz radiation from a TI surface. In general, the contribution of OR is not negligible in P-polarized THz radiation from the semiconductors, such as InAs and GaAs26. Because there is weak S-polarized THz radiation for Cu0.02Bi2Se3 and Bi2Te3, there is no significant modulation in the
-scans in Fig. 3(e,f) also show a three-fold symmetry, which is consistent with the surface crystalline structure of Cu0.02Bi2Se3. A similar symmetry was also recently observed in SHG signal using ultrafast optical pulse illumination in Bi2Se316,17. For p-type Bi2Te3, the same phenomena are also observed, as shown in Fig. 3(c,d,g,h). Consequently, it is concluded that the OR is the main mechanism for S-polarized THz radiation from a TI surface. In general, the contribution of OR is not negligible in P-polarized THz radiation from the semiconductors, such as InAs and GaAs26. Because there is weak S-polarized THz radiation for Cu0.02Bi2Se3 and Bi2Te3, there is no significant modulation in the  -scan results for P-polarized THz radiation, as shown in Fig. 2(e–h).
-scan results for P-polarized THz radiation, as shown in Fig. 2(e–h).
Second-order nonlinear optical process is a simultaneous process in fs time scale and it means that THz pulse originated from OR is generated simultaneously with the incidence of optical pulse. On the other hand, it takes time for the photoexcited electrons, in the 2nd SS and BBs, to relax to the 1st SS or BCB33. This indicates that THz pulse originated from this complex process would lag behind that from OR. Comparing with the P-polarized THz pulses in Fig. 2(a–d), the main peak of the S-polarized THz pulses has a lead of ∼0.2 ps over TIs, as shown in Fig. 3(a–d). This value is closed to the relaxation time 0.5 ps, which is obtained by recent time-resolved ARPES measurement, for the photoexcited electrons from the 2nd SS and BBs relaxing to the 1st SS and BCB33. These results also demonstrate the influence of the 2nd SS and BBs on the P-polarized THz radiation from TIs. In this study, we cannot separate the contribution of the 2nd SS from that of 2nd BBs and the different-wavelength excitation may provide more insights into this unusual phenomenon. We also performed large photon-energy-excitation (central wavelength: 400 nm, Ephoton = 3.1 eV) and the details are presented in Supplementary information.
In summary, we have characterized THz radiation from n-type Cu0.02Bi2Se3 and p-type Bi2Te3 single crystals using ultrafast optical pulse illumination. If an n-type Cu0.02Bi2Se3 single crystal is replaced by a p-type Bi2Te3 single crystal, there is a reversal in the polarity of THz radiation. These results suggest that the drift current  predominates over the transient current in these narrow bandgap materials. This notable phenomenon can be reconciled in the context of the second Dirac surface state and bulk bands. The S-polarized THz radiation results show a three-fold symmetry, which results from the second-order nonlinear optical effect of optical rectification. The present study demonstrates that the second Dirac surface state and bulk bands play the important roles in the optical coupling with the electronic structure of topological insulators.
predominates over the transient current in these narrow bandgap materials. This notable phenomenon can be reconciled in the context of the second Dirac surface state and bulk bands. The S-polarized THz radiation results show a three-fold symmetry, which results from the second-order nonlinear optical effect of optical rectification. The present study demonstrates that the second Dirac surface state and bulk bands play the important roles in the optical coupling with the electronic structure of topological insulators.
Methods
In the experiments, a mode-locked Ti: sapphire oscillator (XL 300, FEMTOLASERS) was used as the light source to generate a 300-nJ optical pulse train with a repetition rate 5.2 MHz and a central wavelength of 800 nm. The pulse duration is ∼75 fs. The output beam was split into two parts by an 80/20 beam splitter. The stronger one was used for THz generation and the weaker one for standard electro-optic sampling. A retro-reflector was mounted on a linear translation stage which was incorporated into the probe-beam path as an optical delay line. A half-wave plate and a cubic polarizer were used to vary the polarization of the optical pump beam. A wire-grid polarizer was used to detect the polarization of the generated THz radiation. Optical pump pulse illuminated the (111) surfaces of the TI crystals at an incident angle of 45° to generate THz radiation. The pulse energy of the pump beam was around 10 nJ and the spot size on the samples was about 280 μm in diameter. For 400-nm excitation, a nonlinear crystal slab, beta-BaB2O4 (BBO) of 0.5 mm in thickness, was used to generate 400-nm optical pulses by second harmonic generation. The THz radiation generated from the TI crystals was collimated by two off-axis parabolic mirrors and focused on a 1-mm-thick <110> ZnTe slab to detect THz radiation. All of the experiments were performed at room temperature and in a chamber filled with nitrogen gas to avoid THz-waveform distortion due to water vapor absorption.
Additional Information
How to cite this article: Tu, C.-M. et al. Manifestation of a Second Dirac Surface State and Bulk Bands in THz Radiation from Topological Insulators. Sci. Rep. 5, 14128; doi: 10.1038/srep14128 (2015).
References
Fu, L., Kane, C. L. & Mele, E. J. Topological insulators in three dimensions. Phys. Rev. Lett. 98, 106803 (2007).
Qi, X.-L., Hughes, T. L. & Zhang, S.-C. Topological field theory of time-reversal invariant insulators. Phys. Rev. B 78, 195424 (2008).
Moore, J. E. The birth of topological insulators. Nature 464, 194–198 (2010).
Hasan, M. Z. & Kane, C. L. Colloquium: Topological insulators. Rev. Mod. Phys. 82, 3045 (2010).
Qi, X.-L. & Zhang, S.-C. The quantum spin Hall effect and topological insulators. Phys. Today 63, 33–38 (2010).
Raghu, S., Chung, S. B., Qi, X.-L. & Zhang, S.-C. Collective modes of a helical liquid. Phys. Rev. Lett. 104, 116401 (2010).
Hosur, P. Circular photogalvanic effect on topological insulator surfaces: Berry-curvature-dependent response. Phys. Rev. B 83, 035309 (2011).
McIver, J. W., Hsieh, D., Steinberg, H., Jarillo-Herrero, P. & Gedik, N. et al. Control over topological insulator photocurrents with light polarization. Nature Nano. 7, 96–100 (2012).
Hsieh, D. et al. A topological Dirac insulator in a quantum spin Hall phase. Nature 452, 970–974 (2009).
Xia, Y. et al. Observation of a large-gap topological-insulator class with a single Dirac cone on the surface. Nature Phys. 5, 398–402 (2009).
Chen, Y. L. et al. Experimental realization of a three-dimensional topological insulator Bi2Te3 . Science 325, 178–181 (2009).
Zhang, T. et al. Experimental demonstration of topological surface states protected by time-reversal symmetry. Phys. Rev. Lett. 103, 266803 (2009).
Roushan, P. et al. Topological surface states protected from backscattering by chiral spin texture. Nature 460, 1106–1109 (2009).
Alpichshev, Z. et al. STM Imaging of electronic waves on the surface of Bi2Te3: topologically protected surface states and hexagonal warping effects. Phys. Rev. Lett. 104, 016401 (2010).
Kim, S. et al. Surface scattering via bulk continuum states in the 3D topological insulator Bi2Se3 . Phys. Rev. Lett. 107, 056803 (2011).
Hsieh, D. et al. Nonlinear optical probe of tunable surface electrons on a topological insulator. Phys. Rev. Lett. 106, 057401 (2011).
McIver, J. W. et al. Theoretical and experimental study of second harmonic generation from the surface of the topological insulator Bi2Se3 . Phys. Rev. B 86, 035327 (2012).
Kumar, N. et al. Spatially resolved femtosecond pump-probe study of topological insulator Bi2Se3 . Phys. Rev. B 83, 235306 (2011).
Luo, C. W. et al. THz generation and detection on Dirac fermions in topological insulators. Adv. Optical Mater. 1, 804–808 (2013).
Luo, C. W. et al. Snapshots of Dirac fermions near the Dirac point in topological insulators. Nano Lett. 13, 5797–5802 (2013).
Sim, S. et al. Ultrafast terahertz dynamics of hot Dirac-electron surface scattering in the topological insulator Bi2Se3 . Phys. Rev. B 89, 165137 (2014).
Sim, S. et al. Tunable Fano quantum-interference dynamics using a topological phase transition in (Bi1-xInx)2Se3 . Phys. Rev. B 91, 235438 (2015).
Eremeev, S. V., Silkin, I. V., Menshchikova, T. V., Protogenov, A. P. & Chulkov, E. V. et al. New topological surface state in layered topological insulators: unoccupied Dirac cone. JETP Lett. 96, 780–784 (2012).
Niesner, D. et al. Unoccupied topological states on bismuth chalcogenides. Phys. Rev. B 86, 205403 (2012).
Sobota, J. A. et al. Direct optical coupling to an unoccupied Dirac surface state in the topological insulator Bi2Se3 . Phys. Rev. Lett. 111, 136802 (2013).
Sakai, K. Terahertz Optoelectronics (Springer Verlag, 2005).
Hsieh, D. et al. A tunable topological insulator in the spin helical Dirac transport regime. Nature 460, 1101–1105 (2009).
Bianchi, M. et al. Coexistence of the topological state and a two-dimensional electron gas on the surface of Bi2Se3 . Nature Commun. 1, 128 (2010).
Urazhdin Bilc, S. D., Mahanti, S. D. & Tessmer, S. H. et al. Surface effects in layered semiconductors Bi2Se3 and Bi2Te3 . Phys. Rev. B 69, 085313 (2004).
ViolBarbosa, C. E. et al. Direct observation of band bending in the topological insulator Bi2Se3 . Phys. Rev. B 88, 195128 (2013).
Galanakis, D. & Stanescu, D. T. Electrostatic effects and band bending in doped topological insulators. Phys. Rev. B 86, 195311 (2012).
Ascázubi, R., Shneider, C., Wilke, I., Pino, R. & Dutta, P. S. et al. Enhanced terahertz emission from impurity compensated GaSb. Phys. Rev. B 72, 045328 (2005).
Sobota, J. A. et al. Ultrafast electron dynamics in the topological insulator Bi2Se3 studied by time-resolved photoemission spectroscopy. J. Electron Spectrosc. Relat. Phenom. 195, 249–257 (2014).
Acknowledgements
This work was supported by the Ministry of Science and Technology of the Republic of China, Taiwan (Grant No. 101-2112-M-009-016-MY2, 102-2112-M-009-006-MY3, 103-2628-M-009-002-MY3, 103-2119-M-009-004-MY3) and the Grant MOE ATU Program at NCTU.
Author information
Authors and Affiliations
Contributions
C.W.L. conceived the research. C.M.T. and S.A.K. developed the experimental setup. C.M.T. performed the THz experiments and analyzed the data. Y.Y.T., W.Y.T. and H.J.C. carried out the XRD measurements of the samples. Y.R.C. contributed to the experiments of 400-nm excitation. C.M.C. and K.D.T. performed the APRES measurements of the samples. H.B., R.S. and F.C.C. synthesized and characterized the samples. The manuscript was prepared by C.M.T. with the assistance from J.Y.L., J.Y.J. and T.K. All authors discussed the results and commented the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Tu, CM., Yeh, TT., Tzeng, WY. et al. Manifestation of a Second Dirac Surface State and Bulk Bands in THz Radiation from Topological Insulators. Sci Rep 5, 14128 (2015). https://doi.org/10.1038/srep14128
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep14128
This article is cited by
-
Charge transfer induced symmetry breaking in GaN/Bi2Se3 topological heterostructure device
npj 2D Materials and Applications (2022)
-
Femtosecond time-evolution of mid-infrared spectral line shapes of Dirac fermions in topological insulators
Scientific Reports (2020)
-
Ultrafast photocurrents at the surface of the three-dimensional topological insulator Bi2Se3
Nature Communications (2016)
-
Possible flat band bending of the Bi1.5Sb0.5Te1.7Se1.3 crystal cleaved in an ambient air probed by terahertz emission spectroscopy
Scientific Reports (2016)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.