Introduction

Since the concept of thermal rectifiers (TR) emerged several decades ago1, a great number of studies have been conducted, placing the emphasis on, respectively, interfacial contact resistances2,3,4, non-uniform mass distributions5, reduced graphene oxide6, nanotubes7, nanowires and nanocones8,9, quantum systems10,11, 1D nonlinear lattices12,13,14, variable thermal conductivities in bi-segment systems15,16, surface/boundary roughness17, liquid and solid interfaces18, photon-based rectification in vacuum19, Y-shaped junctions20, two-dimensional systems21 and finally a comprehensive review22. All these investigations mentioned above share one common interest, which is to maximize rectification effects eventually. If a theoretical limit exists and is known, it may serve as a conducive guidance for future TR designs. Based on the power-law temperature dependence of thermal conductivities, Dames reported a new normalized thermal rectification to better facilitate comparisons of various rectification mechanisms across different temperature ranges23. Here our proposed study focuses on. Here the proposed study focuses on the quest of seeking maxima of rectification ratios, defined as

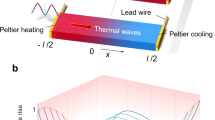
for bi-segment diodes with variable thermal conductivities (Fig. 1(a–d), f: forward; r: reverse). Other similar types of definitions can be readily derived in terms of R. For example, . Figure 1(a) shows the system schematic of a TR consisting of A and B segments, with the upper configuration indicating the forward-flux phase. In Fig. 1(b), we plot κA and κB versus T in the quadratic approximation taken from Ref. [24], whereas Fig. 1(c,d) depict typical linear and nonlinear profiles, respectively.

Figure 1
figure 1

System schematic and various thermal rectifiers considered.

(a) During the forward-flux phase, values of both κA and κB become high, resulting in high heat fluxes. (b) Thermal conductivities of segment materials used in Ref. [24]. (c,d) Typical thermal conductivities of linear and nonlinear thermal rectifiers. The steeper the κ(T) profiles become near T = TH for segment A and near T = TL for segment B, the higher the rectification ratios can attain.

Full size image

To seek an ultimate limit for TRs, we propose some idealized conditions: (1) At the segment junction, there exists a single uniquely-defined temperature and the Kapitza interface resistance25,26 is neglected. If this resistance is considered, the TR equivalently consists of three segments, lying beyond the scope of the present analysis. (2) Steady states prevail all the time. (3) Both segments are perfectly circumferentially insulated such that all variables are functions of x only (one-dimensional).

Linear Thermal Rectifiers

By “linear” TR we mean that both κA and κB are linear functions of T. Let us start with designating p and q as junction temperatures in forward-flux and reverse-flux phases for brevity (“forward”= “eastbound”). A critical intermediate step is to prove that p and q must equal for a given linear TR to reach its Rmax. We first introduce a “temperature potential function” defined as ψA = d1T + d2T2 in segment A and ψB = d3T + d4T2 in segment B, where d1, d2, d3 and d4 are constants used in κA = d1 + 2d2TA and κB = d3 + 2d4TB. The introduction of this function enables us to eliminate the nonlinearity in the energy-conservation equations, such that the relationship, ψi = 0.5(ψi−1 + ψi+1), holds at an arbitrary interior node (Supplementary S-1). At the junction, we obtain slightly more complicated equations as

for the forward-flux phase, and

for the reverse-flux phase, where β = ΔxB/ΔxA, (or β = LB/LA if the same number of uniform grid intervals in segment A and segment B are taken). The subscript “pA” denotes “at the junction location for segment A in the forward-flux phase”; the subscript “j − 1” denotes the node west to the junction. Other subscripts follow similar conventions. Equations (2) and (3) express differences of ψ within a small grid interval Δx. However, since ψ is linear in x, we can safely rewrite Eqs (2) and (3) as βψHA − βψpA = ψpB − ψLB and βψLA − βψqA = ψqB − ψHB, allowing us to express junction temperatures, p and q, directly in terms of boundary conditions as

and

which can be solved analytically for p and q using quadratic formulas when coefficients of quadratic terms are unequal to zero. The subscript “HA” denotes “the location at the high-temperature reservoir for segment A”. For subtle clarity, let us write definitions of all four different boundary ψ′s as

Once p and q are obtained, we can find R with straightforward algebra (Supplementary S-2) as

where κ1 = d1 + d2(TH + p) and κ2 = d1 + d2(q + TL) and finally maximize R by employing the Method of Lagrange Multipliers. There exist two constraints, namely,

for the forward-flux phase, and

for the reverse-flux phase, where κ3 = d3 + d4(p + TL) and κ4 = d3 + d4(q + TH).

Incidentally, associating segment A with d1,d2,κ1 and κ2 and B with d3,d4,κ3 and κ4 will help us to avoid being bewildered by numerous subscripts. Equations (7) and (8) can be combined to eliminate β and the result constitutes the final single constraint as

We are now in the position to introduce the Lagrange function, defined as

With prescribed values of TH, κAL, κAH, κBL and κBH, there remain 3 degrees of freedom left, i.e., p, q and λ. Taking partial differentiation of Eq.(10) with respect to them yields ∂Λ/∂λ = 0, ∂Λ/∂p = 0 and ∂Λ/∂q = 0. The first equation leads to the recovery of the constraint, Eq. (9), itself. Elimination of λ between the second equation and the third eventually yields

where

and

where e1 = dκ1/dp, e3 = dκ3/dp, f2 = dκ2/dq and f4 = dκ4/dq. Equations (9) and (11), lengthy and nonlinear in p and q, can be solved by using the Newton-Raphson method or its modified version (Supplementary S-3). The Lagrange multiplier value, which may sometimes bear physical meanings, can be found by

if its value is needed. The segment-length ratio, βmax = LB/LA and the maximum rectification ratio, Rmax, can also be derived as

corresponding to

and

Note that the influence of d3 and d4 on Rmax is implicitly imbedded in the value of ϕ.

For illustration, let us examine AL1/BL1a (the leftmost TR on the abscissa) (Figs 2 and 3), sandwiched between thermal reservoirs at 120 K and 300 K with segments A and B made of stainless steel and aluminum oxide, respectively. Choosing β = 1 arbitrarily, we use Eqs (4) and (5) to obtain p = 1.3899 and q = 1.9214. Then, from Eq. (6), we obtain R = 1.3260. To optimize this TR, let us modify it into AL1/BL1b with β determined by the method of Lagrange Multipliers, or Eq. (18), to be 2.1618. According to Eq. (17), we succeed in increasing R to 1.3801.

Figure 2
figure 2

Characteristics of twelve thermal rectifiers (TRs).

Here A and B denote “segment A” and “segment B” and L, Q and N, respectively, denote “linear”, “quadratic” and “nonlinear”. The 5th linear TR (counted from the left on the abscissa) (AL4/BL2) is presented to show that rectification effects can take place even if one segment possesses uniform κ. The right most nonlinear TR (AN3/BN3) boasts the highest Rmax, which will become impressive only if materials for AN3 and BN3 can be possibly fabricated on earth and if the thermal contact resistance can be neglected. The values of TH/TL is 2.5 for all TRs except for AL3/BL3 for which we intend to show the fact that does not depend on temperature ranges of thermal reservoirs (TH/TL = 6).

Full size image
Figure 3
figure 3

Thermal conductivities of fifteen segment materials.

The chemical formula for cobalt oxide A and cobalt oxide B take the form of La0.7Sr0.3CoO3 and LaCoO3. For linear segments, κ(T) = d1 + 2d2T; for quadratic segments, κ(T) = d1 + d2T + d3T2; for nonlinear segments AN1 and BN1, ; for nonlinear segments AN2, AN3, BN2 and BN3, . Note that, in all simulations, the grid node for κ staggers half grid interval toward right. Hence, for example, for AN3, κ(TH) = 6067.6 = κmax, but κf(1) = 6064.6, which exhibits a slightly different value. The subscript “M” of κAM shown in the trapezoid stands for “Maximum” (thus “m”=minimum). The variable κAM is shown in the figure merely for the sake of completeness. It is actually not needed in the derivation of Eq. (20).

Full size image

Ultimate Limit for Rectification Ratios of Linear TRS

At this juncture, a question naturally arises: does there exist a rectification-ratio maximum for all linear TRs operating within the same temperature limits? Following this curiosity, we seek the possibility of further increasing the value of Rmax if κAL, κAH, κBL, κBH and TH are varied. The trapezoidal rule dictates (Fig. 3, the top right sub-figure) that

and

where m is the slope of the line for κA(T). Consequently,

First, it is seen from Eq. (17) that Rmax increases as κ1/κ2 increases since (TH − ϕ)/(ϕ − TL) is always positive because 1 < ϕ < TH. Next, assume that (a) x, a1 and a2 are all positive real numbers and (b) a1 < a2. Then an elementary manipulation yields

In Eq. (20), let us regard 2κAm as x, m(ϕ − 1) as a1 and m(ϕ − TL) + m(TH − TL) as a2. Note that m is always positive in segment A. Thus, according to the inequality (21), we are able to conclude

In other words, if we wish to attain the maximum value of κ1/κ2, let us manufacture the segment A such that its thermal conductivity is as low as possible at the low temperature. Similarly, omitting the algebra, we can derive

The constraint, Eq. (9), can now be rewritten as

whose only meaningful solution is found to be

Equation (24) dictates that, when the rectification ratio of a TR reaches its ultimate limit, not only the junction temperatures in the forward-flux phase and the reverse-flux phase must be equal, but also this value must be the average of the temperatures of two thermal reservoirs. Finally, utilizing Eq. (24), we can rewrite Eq. (6) as

which none of rectification ratios of bi-segment linear TRs can possibly exceed. Equation (25) also instructs us that this limit is independent of the temperatures of two thermal reservoirs. In principle, as long as κAm and κBm approach zero, the rectification ratio can approach the value 3 even if the difference between the two reservoir temperatures is very minute. For example, if we are capable of manufacturing a TR, identified as AL2/BL2, by lowering κA from [14.5, 19.5] to [0, 5] and κB from [18.5, 55] to [0, 36.5] without changing slopes, we can attain this limit. Another example is AL3/BL3 (Fig. 2) whose κA(T) and κB(T) lines are fictitiously steep.

Nonlinear Thermal Rectifiers

In the derivation of Rmax for nonlinear TRs, the first critical step remains to be the proof that p and q must be equal when Rmax is reached, or equivalently that two locations, namely, the junction of two segments and the intersection of two temperature profiles, should coincide. For logical clarity, let us arrange reasoning statements step-by-step: (a) κf  > κr is desired everywhere throughout the TR in order for the rectification effect to be pronounced. (b) Equivalently, Tf  > Tr in segment A and Tf < Tr in segment B are desired. (c) If p > q at x = x1(Fig. 4a), the intersection of two T profiles will lie to the right of x1. (d) A small shaded area within which Tf  > Tr will be formed. (e) This area, however, lies in segment B. (f) Statement (e) contradicts statement (b). (g) Hence, the TR shown here cannot be optimal. (h) If p < q at x = x1, the rationale is similar and can be omitted. (i) The proof is established. Extensive simulation results also support this equality condition. Next, let us examine the differential equation governing the temperature distribution in 1D steady-state heat conduction,

Figure 4
figure 4

Temperature distributions taken to explain derivations of

(a) When a TR is not optimized, junction temperatures in forward-flux and reverse-flux phases differ. The intersection of two temperature profiles will lie in either segment A or segment B. (b) When a TR is optimized, we observe that p = q = ϕ and that two profiles intersect nearly like a cross.

Full size image

or

or

where G = (dκ/dT)(dT/dx)2. For uniform κ(or G = 0), the solution of T is simply a straight line as expected. Since dκ/dT is positive in segment A, the term, G, behaves like a heat source, inducing the temperature profile inside segment A to bulge (Fig. 4b). Conversely, in segment B the slope is negative. Thus G behaves like a heat sink, causing the temperature profile to concave. The larger the value of G becomes, the higher the temperature profile tends to convex in segment A, but can never exceed TH, in order to obey the second law of thermodynamics that energy flow cannot travel from a cold body to a hot body by itself. Since p = q = ϕ at the junction, κ bears the same value for both the forward and reverse cases, i. e., κf = κr. According to Eq. (1), (dT/dx)f must be greater than (dT/dx)r in order for R to be greater than unity. By contrast, near x = 0, since both T profiles swell upward, resulting in diminishing Tf gradients and steep Tr gradients, thus it must follow that (dT/dx)f < (dT/dx)r. Consequently, between x = 0 and the junction location, there exists a location where (dT/dx)f = (dT/dx)r. For example, for the TR identified as AN3/BN3 whose temperature distribution looks very similar to Fig. 4b, this location is computed to be x = 0.051m, with temperature gradients equal to 1.98. Hence at that very location, Rmax equals κf/κr, in which the influence of temperature gradients on Rmax entirely vanishes. However, since κf < κmax and κr > κmin, it follows that Rmax = κmax/κmin in segment A. Likewise, Rmax equals κr/κf in segment B. In summary,

where κmax and κmin are two extremes that can be possibly found or fabricated on earth within reasonable temperature ranges on earth today. As an example, for AN1/BN1b, Rmax = 108.8, whereas κ ranges from approximately 0.01 W/mK for low-temperature air up to 5000 W/mK for typical graphene. Hypothetically, if we are able to fabricate two solid materials whose κA increases from 0.01 to 5000 and κB decreases from 5000 to 0.01 as T increases within [120 K, 300 K], the R value cannot exceed a half million.

Two ways of designing high-ratio TRs are recommended: (1) Select materials whose κA(T) varies steeply near TH and κB(T) varies steeply near TL (for example, see Fig. 1d). In this study, since the cross-sectional area of the segments remains uniform, the magnitude of the heat flux (W/m2) depends solely on the product of κ and dT/dx. Exactly at the junction where p = q = ϕ, it is mandatory that κf = κr, implying that R = (dTf/dx)/(dTr/dx) and that the two profiles of Tf(x) and Tr(x) must intersect and resemble a cross at the junction (Fig. 4b), without other alternatives. Subsequently, in order for Tf(x) to vary from φ at the junction to TH at x = 0, it must undergo a sharp bend, then gradually level off near x = 0, again without other alternatives. In order to keep finite the magnitude of G, i. e., (dκ/dT)(dT/dx)2, we must keep the slope, dκ/dT, large to compensate for diminishing values of (dT/dx)x=0. A similar rationale prevails near TL for segment B. Two examples are given in the next section, along with some numerical values of T and κ near the junction. (2) Conduct analyses on each single segment prior to joining the two together, thus permitting time-saving and focusing on characteristics of each segment independently of the other. Accordingly, during the forward-flux phase the 1D stead-state heat conduction phenomenon dictates

which yields

Likewise, during the reverse-flux phase,

We can iteratively tune the value of ϕ such that βf = βr. Afterwards, based on Eq. (1), we can derive

without having to obtain the solution of T(x). Although it does not provide us with Tf(x) and Tr(x), this uni-segment approach yields parametric values of ϕ and βmax, which enable us to entirely separate A and B segments and to predict all characteristics of the bi-segment TR. In other words, with LA, TH and TL given and φ iteratively found from Eqs (31) and (32), we can compute Jf and Jr and thus Rmax for segment A from Eq. (33). These values should be equal to those computed in segment B. Characteristics of AN2/BN2a, b and AN3/BN3 have been obtained using both of this uni-segment procedure and the regular bi-segment simulations.

Comparisons with other Results

Five approaches are adopted to compare their results with those obtained by proposed theoretical and numerical analyses: (a) the experimental in24, (b) in-house micro-scale Hamiltonian-oscillators, (c) assurance that residuals of approximately 4000 nonlinear equations diminish to less than 10−10 upon convergence, (d) assurance that, as the grid-interval number increases from 20 to 2000, the solution gradually reaches an asymptote and (e) identicalness between ϕ and β values obtained by the uni-segment approach and the bi-segment counterpart. In (a), Kobayashi24 et al. reported β = 1.0328 (LA = 0.0061m and LB = 0.0063m) and R = 1.43. Our simulation solution showed R = 1.4452 in fair agreement. In addition, we found that the rectification ratio could increase slightly to Rmax = 1.4623 if the segment-length ratio is modified to βmax = 1.4524. Under this condition, the junction temperature becomes ϕ = 1.7188(or 68.752K) (Fig. 2 and Fig. 5). Incidentally, when R is plotted versus β in an appropriate range, in general a peak emerges for a given TR as shown by two dashed curves in Fig. 5. In (b), we consider Hamiltonian anharmonic oscillators27,28, which are governed by:

Figure 5
figure 5

Comparison of the present simulation result with experimental data24 in good agreement.

Two additional curves for different TRs suggest that generally a given TR can be optimized to achieve its highest R by varying the segment-length ratio β. The inset exhibits the peak more conspicuously.

Full size image

where n is the total number of particles; mi the mass of particles; pi the momentum of the ith particle; xi the displacement from the equilibrium position; k the strength of the inter-particle harmonic potential; and γ the strength of the on-site potential. In Fig. 6, temperature profiles obtained by using Eq. (34) is plotted versus the oscillator number or x. In 1D-chain-oscillator analyses, usually κ is deduced from the temperature gradient and the heat flux, instead of being given in bulk-system heat conduction analyses. Thus, post-processing with curve-fitting yields κ(T) = 0.049(0.331 + T)−1.369, which in turn serves as an input into the macro-scale uni-segment simulation code. The solutions, representing temperature profiles in B segment, are seen to agree fairly. In (c), for clarity of illustration, let us select the TR, identified as AN2/BN2b and consider the energy balance over the control volume containing the junction node where troubles of solution divergence, if any, usually originate. Nodal temperatures at two adjacent nodes and thermal conductivities at two adjacent mid-points are listed:

Figure 6
figure 6

Comparison of temperature distributions obtained by running micro-scale Hamiltonian-oscillator simulations and macro-scale uni-segment numerical simulations.

In the former κ is computed, whereas in the latter κ is given. Both profiles concave as they should in segment B, which behaves as if a heat sink prevails.

Full size image

To derive the governing equation for the junction temperature, T1001, we write, for the forward-flux case,

The fact that the left-hand side is equal to the right-hand side (Jf = 559.1107) partly suggests that the code is bug-free. Similarly, Jr = 0.52516. Therefore, we obtain Rmax = Jf/Jr = 1064.66 (Fig. 2). In (d), for AN3/BN3, which exhibits the steepest temperature slope near the junction among all TRs, we repeat runs for nA = nB = 20, 40, 100, 200, 500, 1000 and 2000 and obtain an asymptotic value of 3121 for Rmax as nA approaches 2000. Results for AN2/BN2b are obtained using both the uni-segment procedure and the regular bi-segment simulation and are found to be the same.

The TR system is discretized into nA + nB grid intervals, where nA = nB = 1000 was taken for nonlinear TRs. A modified Newton-Raphson method29, in which nonlinear terms were not linearized if unnecessary, was used to solve the set of these nonlinear equations. To ensure the solution convergence, we monitored maximum residuals of nodal flux differences (west value minus east value for node i) and thermal conductivity differences (computed value minus analytical value). These values diminish to O(10−10) except those for forward fluxes in AN2/BN2 and AN3/BN3, of which values vanish to O(10−8). The 1D chain of anharmonic oscillators is connected to two thermal reservoirs at TH = 2.5 and TL = 0.5. Langevin30 thermal baths are used, leading to boundary conditions for oscillators (i = 1) and (i = 64) as

and

where

Symbols a1, a2, a3 and a4 are randomly-generated numbers between 0 and 1; values of λw, λe (damping factors), k, κB and γ are all taken to be unity. The set of 64 nonlinear equations of motion are integrated by using the fourth-order stochastic Runge-Kutta algorithm31.

In practice, very few TRs can strictly remain in steady state all the time. Immediately after the thermal reservoirs are switched, the TR will experience a change to adjust itself thermally to a new state. During this transient period, Eq. (27) should be modified to

Even though the problem has now become slightly more complicated, there exists a possibility that the transient term on the right hand side of Eq. (38) can be manipulated to increase rectification ratios. Such an exploration will be left as the future work.

Additional Information

How to cite this article: Shih, T.-M. et al. Maximal rectification ratios for idealized bi-segment thermal rectifiers. Sci. Rep. 5, 12677; doi: 10.1038/srep12677 (2015).