Abstract
A general class of prototype dynamical systems is introduced, which allows to study the generation of complex bifurcation cascades of limit cycles, including bifurcations breaking spontaneously a symmetry of the system, period doubling and homoclinic bifurcations and transitions to chaos induced by sequences of limit cycle bifurcations. The prototype systems are adaptive, with friction forces f(V(x)) being functionally dependent exclusively on the mechanical potential V(x), characterized in turn by a finite number of local minima. We discuss several low-dimensional systems, with friction forces f(V) which are linear, quadratic or cubic polynomials in the potential V. We point out that the zeros of f(V) regulate both the relative importance of energy uptake and dissipation respectively, serving at the same time as bifurcation parameters, hence allowing for an intuitive interpretation of the overall dynamical behavior. Starting from simple Hopf- and homoclinic bifurcations, complex sequences of limit cycle bifurcations are observed when the energy uptake gains progressively in importance.
Similar content being viewed by others
Introduction
The term ‘prototype dynamical system’ is employed for generic, but otherwise reduced systems, allowing to study and to understand a certain relevant phenomenon (like dynamical behavior and/or bifurcation scenario). For this, the dynamical behavior of the system should be dominated by the prime phenomenon of interest, with the system being otherwise simple enough to allow for straightforward numerical and (at least partial) analytic investigations1,2,3,4. Additionally, their dynamical behavior can often be understood in terms of general concepts, such as energy balance, symmetry breaking, etc.
Examples of prototype systems are the normal forms of standard bifurcation analysis5,6 and classical systems, like the Van der Pol oscillator5, or the Lorenz model7, which have been of central importance for the development of dynamical systems (systems) theory. As an example we consider the Liénard equation,

a generic adaptive mechanical system, which includes the Van der Pol oscillator and the Takens-Bogdanov system8,9. The periodically forced extended Liénard systems with a double-well potential have also been studied by many authors (see e.g. the double-well Duffing oscillator10,11,12).
In this paper we propose a new class of autonomous Liénard-type systems, which allow to study cascades of limit cycle bifurcations, using a bifurcation parameter controlling directly the balance between energy dissipation and uptake and hence the underlying physical driving mechanism. Though there are a range of alternative construction methods for dynamical systems in the literature (see e.g.13,14,15), they generally involve abstract concepts, such as implicitly defined manifolds, or mathematical tools accessible only to researchers with an in-depth math training. In contrast to these methods, we provide here a mechanistic design procedure, based on the construction of attractors through the interaction of generalized friction forces with potential forces, an intuitive concept especially suitable for interdisciplinary investigations (e.g. in modeling cardiovascular systems16 or for solving optimization problems17), making it easily accessible and implementable for other scientific communities (such as neuroscience, biology etc.) as well.
As an introductory example for the role of balance between energy uptake and dissipation, in both local and global bifurcations, we reconsider the Bogdanov-Takens system,

which is often used as a prototype system for homoclinic bifurcations5. Here, the mechanical potential is a third order polynomial, as illustrated in Fig. 1. The friction force is directly proportional to the velocity y, hence fixpoints of (2) correspond to the minima and the maxima of the potential V(x).
The Bogdanov-Takens system (2) with the potential function V(x) = x3/3 − x2/2 and a friction term x − μ (top row) and its generalization (4) to a friction term μ1 − V(x) (bottom row), compare Eq. (6). Left column: The potential function together with the color-coded regions of energy dissipation and uptake respectively, compare Eq. (3). Right column: The phase planes at the respective homoclinic bifurcation points, with the unstable foci and the saddles denoted by open circles. The green and blue trajectories are the stable and unstable manifolds, while the red trajectory corresponds to the homoclinic loop.
The dynamics of the Bogdanov-Takens system is controlled by the parameter μ, defining, in terms of the mechanical energy E, the regions of dissipation and energy uptake in the potential valley,

compare Fig. 1. The region x > μ of energy uptake increases when the bifurcation parameter μ is decreased, leading to two consecutive transitions. Initially the potential minimum becomes repelling, undergoing a supercritical Hopf bifurcation and a stable limit cycle emerges. Decreasing μ further, the extension of the limit cycle increases, merging at μc with the stable and unstable manifolds of the saddle, resulting in a homoclinic bifurcation.
Results
The key mechanism leading to the bifurcations in the Bogdanov-Takens systems is the availability of a parameter, allowing to change the balance between energy uptake and energy dissipation along limit cycles. Our aim is to generalize this idea to the case of mechanical systems characterized by an arbitrary number of potential minima. For this purpose we consider

which describes a 2d—dimensional system, with d spatial coordinates and friction forces f(V(x)) depending functionally only on the mechanical potential V(x), allowing for a fine-tuned control of the energy dissipation and uptake around the respective potential minima. A well known example of a system of type (4) is the Van der Pol oscillator:

for which the regions of energy uptake and dissipation remain fixed, with ε regulating the overall influence of the velocity-dependent force.
The simplest generic class of friction functions f(V) entering (4) are polynomial:

where α regulates the overall strength of the friction and the individual μ1 < μ2 < μ3 are the respective zeros, the points at which dissipation changes to anti-dissipation and vice versa, compare Fig. 2.
Left column: Double well potential, as defined by Eq. (7), with x1,2 = ±1, V1,2 = 0, z1,2 = 1 and p1,2 = 1.The regions of energy dissipation  and uptake
and uptake  are color coded. For the friction functions (6) we used f1 with α = 1 (top row), f2 with μ2 = 0.6 and α = 5 (middle row) and f3 with μ2 = 0.3, μ3 = 0.6 and α = 5 (bottom row). Right column: Bifurcation diagrams of the respective generalized Liénard systems (4), functions of μ1. All other μi (when present) are kept constant. Stable/unstable fixpoints or limit cycles are denoted by continuous/dashed curves respectively. Black lines are fixpoint lines, while the maximal/minimal amplitude of x in a cycle is denoted with red/green color. H points denote Hopf bifurcations, HO corresponds to homoclinic bifurcations of a saddle, SNC points denote saddle node bifurcations of limit cycles. The dotted, dashed and continuous vertical gray lines are just guides for the eyes.
are color coded. For the friction functions (6) we used f1 with α = 1 (top row), f2 with μ2 = 0.6 and α = 5 (middle row) and f3 with μ2 = 0.3, μ3 = 0.6 and α = 5 (bottom row). Right column: Bifurcation diagrams of the respective generalized Liénard systems (4), functions of μ1. All other μi (when present) are kept constant. Stable/unstable fixpoints or limit cycles are denoted by continuous/dashed curves respectively. Black lines are fixpoint lines, while the maximal/minimal amplitude of x in a cycle is denoted with red/green color. H points denote Hopf bifurcations, HO corresponds to homoclinic bifurcations of a saddle, SNC points denote saddle node bifurcations of limit cycles. The dotted, dashed and continuous vertical gray lines are just guides for the eyes.
When using f1(V) and the mechanical potential V(x) = x3/3 − x2/2, the resulting flow in phase space is equivalent to the one of the Bogdanov-Takens system (2), as shown in Fig. 1.
Generalized mechanical potentials
We are interested in using (4) as prototype dynamical systems, especially for the case of non-trivial mechanical potentials V(x) having an arbitrary number M of local minima. One could in principle consider higher-order polynomials for this purpose, however these do not allow to control the overall height of the potential and the relative width of the local minima in as simple a fashion.
For this purpose we use throughout this study potential functions of the kind

where the zn > 0 determine the half-width of the respective local minima and the pn satisfy the self-consistent condition:

since g(0) = 0. For deep minima, with (zi + zj) ≪ |xi − xj|, the positions and the heights of the local minima are close to xn and Vn respectively. We found that a relative accuracy of 10−2 for Vn can already be achieved in general after three or four iterations.
Limit cycle bifurcation cascades
The system of type (4) allows to describe complex cascades of limit cycle bifurcations. In Fig. 2 we show some illustrative examples, using a symmetric double-well potential and linear/quadratic/cubic friction functions f1(V)/f2(V)/f3(V) respectively, see Eq. (6). We used numerical methods (see the Methods section) to obtain the respective full bifurcation diagrams, with solid/dashed lines denoting stable/unstable fixpoints and limit cycles. The corresponding flow in phase space is illustrated in Fig. 3.
Flow diagrams for the systems presented in Fig. 2, using respectively linear/quadratic/cubic friction functions f1(V)/f2(V)/f3(V) (top/middle/bottom row). The values  ,
,  and
and  for the respective μ1 are indicated by arrows in the corresponding bifurcation diagrams in Fig. 2.
for the respective μ1 are indicated by arrows in the corresponding bifurcation diagrams in Fig. 2.
For negative μ1 the two fixpoints (±1, 0) are stable, for the case of f1(V) and f3(V) and stable limit cycles evolve via two supercritical Hopf bifurcations (bifurcations). For f2(V), on the other hand, a subcritical Hopf bifurcation is observed at μ1 = 0. The respective stable/unstable limit cycles merge for f1(V) and f2(V) in a homoclinic bifurcation, whereas a more complex bifurcation diagram emerges for f3(V). Saddle node bifurcations of limit cycles are present for both f2(V) and f3(V).
Chaos via period doubling of limit cycles
We consider now a prototype system (4) with a two-dimensional symmetric potential function V(x),

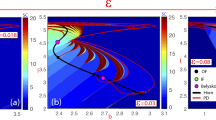
as defined in (7), having two minima x1,2 = ±(1, −1) and a linear friction term f1(V) = 0.5(μ − V). Both diagonals in the (x1, x2) plane are symmetry axes of the system, as discussed in the Methods section. In Fig. 4 we present examples of stable limit cycles and of a chaotic trajectory, as projected to the (x1, x2) plane. In Fig. 5 the corresponding bifurcation diagram is presented. The diagram shows Hopf bifurcations (H), homoclinic bifurcations (HO), branching of limit cycles via spontaneous symmetry breaking (SSB), period doubling of limit cycles (PD) and a transition to chaotic behavior:
Stable limit cycles and chaotic orbits of the Liénard prototype system (4) in a two-dimensional symmetric double well potential V(x) (color coded, as defined by Eq. (9)) and with a linear friction term f1(V(x)) = 0.5 (μ1 − V(x)). The bifurcation parameter μ1 is 0.1, 0.15, 0.25, 0.265, 0.2698, 0.3 from (a) to (f). In (d) the four limit cycles can be mapped onto each other by using the symmetry operations σ1,2 or σ3,4, as discussed in the Methods section. For (e) only a single of the four stable limit cycles is shown. This needs to circle the two potential minima twice in order to retrace itself. In (f) an example of a chaotic trajectory is given.
Top row: The numerically obtained bifurcation diagram for a four-dimensional prototype Liénard system with symmetric double-well potential and a linear friction force, as for Fig. 4. The second branches of limit cycles emerging from the two destabilized minima (see Supplementary Fig. S1) are not shown here. One observes Hopf and homoclinic bifurcations (H and HO), branching of limit cycles via spontaneous symmetry breaking and period doubling (SSB and PD), as well as a transition to chaos for μ1 > 0.2705. The red/green lines indicate the maximal/minimal x1-values of the respective limit cycles. The blue curve is the second x1-maxima after period doubling. The right diagram represents a zoom-in of the transition to a chaotic region, indicated by the shaded green and red areas. Only the first two period doubling bifurcations are shown. Bottom row: The average Lyapunov exponent  and the contraction rate σ, calculated as described in the Methods section, for the corresponding μ1 parameter intervals. For the left figure Δμ1 = 0.001 parameter stepsize was used. Increasing the resolution more and more periodic windows (with
and the contraction rate σ, calculated as described in the Methods section, for the corresponding μ1 parameter intervals. For the left figure Δμ1 = 0.001 parameter stepsize was used. Increasing the resolution more and more periodic windows (with  ) become visible, as shown on the right plot, where Δμ1 is decreased by a factor of ten.
) become visible, as shown on the right plot, where Δμ1 is decreased by a factor of ten.
H At  the two potential minima become unstable, just as for the one-dimensional spatial system presented in Fig. 2, resulting in two equivalent supercritical Hopf bifurcations. We note that, as a result of the symmetric potential function (9), a second branch of limit cycles is created by the two Hopf bifurcations (see the discussion in the Methods section and the Supplementary Information). However, since in the parameter region of interest these limit cycles are mostly unstable, we have not investigated them in detail.
the two potential minima become unstable, just as for the one-dimensional spatial system presented in Fig. 2, resulting in two equivalent supercritical Hopf bifurcations. We note that, as a result of the symmetric potential function (9), a second branch of limit cycles is created by the two Hopf bifurcations (see the discussion in the Methods section and the Supplementary Information). However, since in the parameter region of interest these limit cycles are mostly unstable, we have not investigated them in detail.
HO At  the limit cycles merge, as in Fig. 4(a,b), in a homoclinic transition. The limit cycle stays, however, exactly on the diagonal x1 + x2 = 0.
the limit cycles merge, as in Fig. 4(a,b), in a homoclinic transition. The limit cycle stays, however, exactly on the diagonal x1 + x2 = 0.
SSB At the first branching point of limit cycles,  the symmetry with respect to the diagonal (1, −1) is spontaneously broken, as in Fig. 4(b,c), with the two limit cycles still being symmetric with respect to the (1, 1) diagonal. The latter symmetry is broken at the second branching point
the symmetry with respect to the diagonal (1, −1) is spontaneously broken, as in Fig. 4(b,c), with the two limit cycles still being symmetric with respect to the (1, 1) diagonal. The latter symmetry is broken at the second branching point  , as in Fig. 4(c,d), creating four symmetry related stable limit cycles.
, as in Fig. 4(c,d), creating four symmetry related stable limit cycles.
PD For larger values of the bifurcation parameter μ1 a series of period-doubling of limit cycles is observed, with the first occurring at  , as in Fig. 4(d,e). The next period-doubling transition occurs at
, as in Fig. 4(d,e). The next period-doubling transition occurs at  , as shown in Fig. 5.
, as shown in Fig. 5.
For reference we note that the saddle of the potential is located at V(0, 0) = 0.505, viz at a substantially larger value.
For  we observe seemingly chaotic trajectories, as illustrated in Fig. 4(f). Studying the transition to chaos is not the subject of the present investigation and we leave it to future work. We presume however, that the transition occurs via an accumulation of an infinite number of of period-doubling transitions of limit cycles, similar to the ones observed for the Lorenz system18 and for the Rössler attractor19,20.
we observe seemingly chaotic trajectories, as illustrated in Fig. 4(f). Studying the transition to chaos is not the subject of the present investigation and we leave it to future work. We presume however, that the transition occurs via an accumulation of an infinite number of of period-doubling transitions of limit cycles, similar to the ones observed for the Lorenz system18 and for the Rössler attractor19,20.
Our prototype system (4) is not generically dissipative. We have evaluated the average contraction rate σ, as defined by (22) in the Methods section and presented the results in Fig. 5. Phase space contracts trivially along the attracting limit cycles, but also, on average, in the chaotic region, where the average Lyapunov exponent  becomes positive.
becomes positive.  is negative for μ1 < 0, when only stable fixpoints are present, vanishing for intermediate values of μ1, when stable limit cycles are present. The later is due to the fact, see Fig. 7 and the corresponding Methods section, that two initially close trajectories will generally flow to the same limit cycle with the relative distance becoming constant.
is negative for μ1 < 0, when only stable fixpoints are present, vanishing for intermediate values of μ1, when stable limit cycles are present. The later is due to the fact, see Fig. 7 and the corresponding Methods section, that two initially close trajectories will generally flow to the same limit cycle with the relative distance becoming constant.
The logarithmic growth rate 〈ln(Δr)〉 averaged for 100 random initial conditions as a function of time for three qualitatively different types of dynamics: spiraling into a fixpoint (μ1 = −0.05), limit cycle oscillations (μ1 = 0.2) and chaotic behavior (μ1 = 0.3). Brown lines correspond to the best linear regression. In the first and last case, the line is fitted only to the first part of the trajectory. The dashed line indicates that the distance of the point pairs has reached the maximal accuracy of the integrator.
For larger values of μ1 > 0.322 the chaotic region transforms into a phase of intermittent chaos as illustrated in Fig. 6, in which an extended quasi-regular flow along the (−1, 1) diagonal is interseeded by a roughly perpendicular bursting flow. This behavior is, to a certain extend, reminiscent to a scenario of intermittent chaos21, in which a strange attractor is embedded in a higher-dimensional space with partly unstable directions. We have, however, not investigated the observed intermittent dynamics in detail.
Left: Quasi-periodic windows with different time scales in the time-series plot of x1 for μ1 = 0.34. Right: Phase space plot of the trajectory projected to the (x1, x2) plane for the same parameter. The magenta curve corresponds to the quasi-periodic time interval tp = [4 ⋅ 103, 12 ⋅ 103], denoted with the same color in the x1(t) plot.
Discussion
We have proposed and discussed a prototype dynamical system (4) in which the friction forces ∝ f(V) depend functionally only on the mechanical potential V(x). We have shown that complex cascades of limit cycle bifurcations can be obtained even for two dimensional phase spaces, when the friction function f(V) alternates between regions of energy uptake and dissipation.
We have also introduced a generic class of potential functions (7), which allows to define, in a relative straightforward manner, mechanical potentials with an arbitrary number of local minima and varying depth. Considering a simple double-well prototype system with two spatial dimensions (and with a four-dimensional phase space), we have shown that symmetry induced bifurcations of limit cycles and period-doubling of limit cycle transition to chaotic behavior can occur.
As discussed in the Methods section, the presence of stable and unstable fixpoints, the birth of limit cycles through transition from dissipation to energy uptake in the neighborhood of the local minima, or the symmetry properties of the prototype system do not depend on the particular method used to construct the potential function. The only requirement it has to fulfill is the existence of a certain number of local minima.
Hence, other potential functions could also be considered. For example, one could study the biquadratic version

of the potential (9), used in our study of chaotic behavior with the prototype system (4). We did not study in detail the bifurcation diagram for the potential function (10), however, we have checked that one would get similar results to the ones presented in Figs 4 and 5, having the same underlying driving mechanism in terms of a linear friction function f(V) ∝ (μ1 − V). For increasing values of the μ1 control parameter, first stable fixpoints, then spatially separated-, merging- and symmetry breaking limit cycles can also be observed. Furthermore, using the potential function (10) chaotic behavior has also been found.
As a future perspective, we note that by changing the depth of the minima, one could control the order in which the fixpoints are going to be destabilized, which might lead to other interesting phenomena. Adding an extra (maybe slow) dynamics to the positions or depths of the minima, the metadynamics of the attractors22 may also be considered. In this case the pn parameters should be recalculated in each time-step using the self-consistent equations (8), which proved to be fast enough for practical purposes.
Models, for which the equations of motion are derived from higher order principles, provide promising results for the understanding of many different phenomena, such as the optimization hardness of boolean satisfiability problems17 or the complex dynamics of biological neural networks23,24. Generally, these methods involve the construction of a generating functional, such as the cost function or energy functional25,26,27,28, with the dynamics of the system being defined by a gradient decent rule. When all equations are derived from the same generating functional, the system corresponds mathematically to a gradient system for which the asymptotic behavior is determined by stable fixpoints (nodes). They can thus not produce limit cycles or oscillatory behaviors. To by-pass this problem, additional equations of motions are usually defined, derived either from a second generating functional, to induce objective function stress29,30, or from other considerations. In our model, the system has an inherent inertia, which, in the presence of dissipation, leads to damped oscillations around the equilibria (minima of the potential). By creating regions of antidissipation, stable oscillatory dynamics and chaotic behavior is stabilized. Considering nonsymmetric and/or higher dimensional potential functions, we expect to find an even richer set of dynamical behaviors (see the Methods section), a scenario worth to be investigated in the future. As a possible application one could use the system for modeling the dynamics of various, complex and adaptive dynamical systems, for which the generalized potential function (energy landscape, cost functional, etc.) is approximated by (8) or is found from some other considerations. An alternative type of prototype dynamical system has been shown to be useful for understanding the coexistence of spiking and bursting neural activity observed in electrophysiological experiments2.
Finally, we note that the concepts of dynamical systems theory, such as attractors, slow points and bifurcations have been used recently to understand phenomena of surprisingly diverse fields. We mention here the modeling of birdsongs31 and migraine dynamics32 and the control mechanisms for the movements of humanoid robots33. The common approach, considered in these works, is the aim to construct simple and, to a certain extend, idealized dynamical systems, which allow for an in-depth understanding of certain dynamical behaviors. We hence believe that prototype systems allowing, in an intuitive manner, for the construction of models with a predefined set of attractors, as presented here, could offer a useful tool for understanding the behavior of a range of interesting interdisciplinary problems.
Methods
The bifurcation diagrams shown in Figs 2 and 5 have been constructed by using the PyDSTool34 software package. In this section we provide the analytic calculations for the study of fixpoint stability for 2-, 3- and 2d-dimensional prototype systems respectively. We note that, these properties are valid irrespective of the particular shape considered for the potential function. This is followed by a discussion of symmetry properties and presentation of numerical methods used to estimate the average Lyapunov exponent and the contraction rate.
Hopf bifurcations in the prototype system
2-dimensional prototype systems
The local maxima of the potential function, i.e. where  , which are saddle points, separate the phase plane into different attraction domains with their stable manifold. Local minima with
, which are saddle points, separate the phase plane into different attraction domains with their stable manifold. Local minima with  become, on the other hand, repelling focuses as a result of an Andronov-Hopf bifurcation, when dissipation changes to antidissipation in their neighborhood, having a simple pair of purely imaginary eigenvalues
become, on the other hand, repelling focuses as a result of an Andronov-Hopf bifurcation, when dissipation changes to antidissipation in their neighborhood, having a simple pair of purely imaginary eigenvalues  .
.
4-dimensional prototype systems
Analogously, the

fixpoints of the 4-dimensional prototype systems (4) correspond to critical points of the V(x1, x2) potential function. Classification of the local minima and saddle critical points with respect to their stability can be achieved by evaluating the eigenvalues of the Jacobian of the system in terms of the Hessian of the potential function:

where we have defined the friction term and the second order partial derivatives of the potential at the respective critical points as

Defining also

we can express the eigenvalues of the Jacobian J(q*) as

For general potential functions the local minima, defined by the conditions Δ = det(H) = d1d2 − c2 > 0 and ρ = tr(H) = −(d1 + d2) < 0 (or equivalently by γ± > 0), undergo a Hopf bifurcation, when the f(V) friction term changes sign, i.e.:

However, saddles of the potential function, i.e. Δ = det(H) < 0, are saddle type fixpoints of the dynamical system, having always a positive eigenvalue, as γ+ > 0 and γ− < 0.
Here we note that in case of the potential function (9), due to the symmetries one gets a double pair of imaginary eigenvalues, since d1 = d2 and c = 0 and thus Eq. (13) yields γ+ = γ−. This results in a second branch of limit cycle solutions, not investigated in this paper, emerging from the Hopf-point.
2d-dimensional prototype systems
For arbitrary dimensions d one can express the Jacobian in terms of block matrices:

where a = f(V) and where Od and Id are the d-dimensional zero and identity matrices.  is the Hessian matrix of the potential, evaluated for the respective q* = (x*, y*) fixpoints.
is the Hessian matrix of the potential, evaluated for the respective q* = (x*, y*) fixpoints.
To determine the eigenvalues of the Jacobian one has to solve the equation:

where we used the properties of square block matrices. By introducing γ = λ(a − λ) on finds with

that the 2d eigenvalues λi± of the Jacobian can be expressed in terms of the d eigenvalues γi of the Hessian matrix and hence

Consequently, at the local minima of the potential, i.e. when γi > 0, a Hopf-bifurcation occurs, with  , when the friction term a = f(V) changes sign. For general potential functions this might lead to the birth of higher dimensional tori or several branches of limit cycle bifurcations.
, when the friction term a = f(V) changes sign. For general potential functions this might lead to the birth of higher dimensional tori or several branches of limit cycle bifurcations.
Symmetries of the 4-dimensional system
The results shown in Figs 4,5 and 6 are found for the 4-dimensional prototype systems (4) with a linear friction force f1(V), as defined by (6) and a mechanical potential V(x) given by (9). The minima V(x1,2) = 0 of the potential, viz. x1 = (+1, −1) and x2 = (−1, +1) are connected by the symmetry operations

of the system. Thus, if (x1, x2, y1, y2) is a solution, then

are also solutions.
As one could expect from the definition of the class of prototype systems introduced here (see Eq. (4)), the symmetry properties of the system are closely related to the particular symmetries of the potential function considered for modeling a certain behavior. Thus, finding the corresponding σi symmetry operations, could reveal new limit cycle solutions related by symmetry.
Lyapunov exponent and contraction rate
The local Lyapunov exponent λ is determined from the growth rate of the distance Δr(t) = Δr0eλt, between point pairs with an initial displacement, which we have taken to be Δr0 = 10−8. The measurement of the Lyapunov exponent was started after a transient of ttr = 1.5 ⋅ 104. Considering 100 random initial conditions the average Lyapunov exponent  is then given by the slope of the initial linear part of the 〈ln(Δr)〉 curve (as given by the brown lines in Fig. 7).
is then given by the slope of the initial linear part of the 〈ln(Δr)〉 curve (as given by the brown lines in Fig. 7).
The contraction rate σ, is defined as the average of local contraction rates along a set of trajectories Γ for different initial conditions:

where L = ∫Γ ds is the length of the trajectory and f is the flow, viz the right-hand side of the evolution equations (4). σ is negative for dissipative systems, in which the phase space contracts5,6.
Additional Information
How to cite this article: Sándor, B. and Gros, C. A versatile class of prototype dynamical systems for complex bifurcation cascades of limit cycles. Sci. Rep. 5, 12316; doi: 10.1038/srep12316 (2015).
References
Dangelmayr, G. & Kirby, M. On diffusively coupled oscillators. In Allgower, E., Böhmer, K. & Golubitsky, M. (eds) Bifurcation and Symmetry. 85–97 (Birkhäuser Basel, 1992).
Cymbalyuk, G. S., Calabrese, R. L. & Shilnikov, A. L. How a neuron model can demonstrate co-existence of tonic spiking and bursting. Neurocomputing 65, 869–875 (2005).
Uçar, A. On the chaotic behaviour of a prototype delayed dynamical system. Chaos, Solitons & Fractals 16, 187–194 (2003).
Krupa, M., Popovic, N. & Kopell, N. Mixed-mode oscillations in three time-scale systems: a prototypical example. SIAM Journal on Applied Dynamical Systems 7, 361–420 (2008).
Gros, C. Complex and adaptive dynamical systems: A primer (Springer, 2013).
Chow, S.-N., Li, C. & Wang, D. Normal forms and bifurcation of planar vector fields (Cambridge University Press, 1994).
Lorenz, E. N. Deterministic nonperiodic flow. Journal of the atmospheric sciences 20, 130–141 (1963).
Takens, F. Singularities of vector fields. Publications Mathématiques de l’IHÉS 43, 47–100 (1974).
Bogdanov, R. I. Versal deformations of a singular point of a vector field on the plane in the case of zero eigenvalues. Functional analysis and its applications 9, 144–145 (1975).
Venkatesan, A. & Lakshmanan, M. Bifurcation and chaos in the double-well Duffing - Van der Pol oscillator: Numerical and analytical studies. Physical Review E 56, 6321–6330 (1997).
Yamaguchi, A., Fujisaka, H. & Inoue, M. Static and dynamic scaling laws near the symmetry-breaking chaos transition in the double-well potential system. Physics Letters A 135, 320–326 (1989).
Li, R., Xu, W. & Li, S. Chaos controlling of extended nonlinear Liénard system based on the Melnikov theory. Applied Mathematics and Computation 178, 405–414 (2006).
Sandstede, B. Constructing dynamical systems having homoclinic bifurcation points of codimension two. Journal of Dynamics and Differential Equations 9, 269–288 (1997).
Deng, B. Constructing homoclinic orbits and chaotic attractors. International Journal of Bifurcation and Chaos 04, 823–841 (1994).
Qi, G., Du, S., Chen, G., Chen, Z. & Yuan, Z. On a four-dimensional chaotic system. Chaos, Solitons & Fractals 23, 1671–1682 (2005).
Regan, E. R. & Aird, W. C. Dynamical systems approach to endothelial heterogeneity. Circulation research 111, 110–30 (2012).
Ercsey-Ravasz, M. & Toroczkai, Z. Optimization hardness as transient chaos in an analog approach to constraint satisfaction. Nature Physics 7, 966–970 (2011).
Robbins, K. Periodic solutions and bifurcation structure at high r in the Lorenz model. SIAM Journal on Applied Mathematics 36, 457–472 (1979).
Rössler, O. E. An equation for continuous chaos. Physics Letters A 57, 397–398 (1976).
Gardini, L. Hopf bifurcations and period-doubling transitions in Rössler model. Il Nuovo Cimento B Series 11 89, 139–160 (1985).
Lai, Y.-C. Symmetry-breaking bifurcation with on-off intermittency in chaotic dynamical systems. Physical Review E 53, R4267 (1996).
Gros, C., Linkerhand, M. & Walther, V. Attractor metadynamics in adapting neural networks. In Artificial Neural Networks and Machine Learning–ICANN 2014, vol. 8681 of Lecture Notes in Computer Science. 65–72 (Springer, 2014).
Markovic, D. & Gros, C. Self-organized chaos through polyhomeostatic optimization. Physical Review Letters 105, 068702 (2010).
Marković, D. & Gros, C. Intrinsic adaptation in autonomous recurrent neural networks. Neural Computation 24, 523–540 (2012).
Intrator, N. & Cooper, L. N. Objective function formulation of the bcm theory of visual cortical plasticity: Statistical connections, stability conditions. Neural Networks 5, 3–17 (1992).
Triesch, J. A gradient rule for the plasticity of a neuron’s intrinsic excitability. In Artificial Neural Networks: Biological Inspirations–ICANN 2005. 65–70 (Springer, 2005).
Friston, K. The free-energy principle: a unified brain theory? Nature Reviews Neuroscience 11, 127–138 (2010).
Prokopenko, M. Guided self-organization: Inception. vol. 9 (Springer, 2013).
Linkerhand, M. & Gros, C. Generating functionals for autonomous latching dynamics in attractor relict networks. Scientific Reports 3, 2042 (2013).
Gros, C. Generating functionals for guided self-organization. In Prokopenko, M. (ed.) Guided Self-Organization: Inception 53–66 (Springer, 2014).
Sitt, J. D., Amador, a., Goller, F. & Mindlin, G. B. Dynamical origin of spectrally rich vocalizations in birdsong. Physical Review E 78, 011905 (2008).
Dahlem, M. A. Migraine generator network and spreading depression dynamics as neuromodulation targets in episodic migraine. Chaos 23, 046101 (2013).
Ernesti, J., Righetti, L., Do, M., Asfour, T. & Schaal, S. Encoding of periodic and their transient motions by a single dynamic movement primitive. In Humanoid Robots (Humanoids), 2012 12th IEEE-RAS International Conference on 57–64 (2012).
Clewley, R. Hybrid models and biological model reduction with PyDSTool. PLoS Computational Biology 8, e1002628 (2012).
Acknowledgements
The work of B.S. was supported by the European Union and the State of Hungary, co-financed by the European Social Fund in the framework of TÁMOP 4.2.4.A/2-11-1-2012-0001 National Excellence Program. We thank C. Drukier for carefully reading the manuscript.
Author information
Authors and Affiliations
Contributions
Both authors, B.S. and C.G., contributed equally to the research and to the preparation of the manuscript, B.S. prepared the figures. All authors reviewed the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Sándor, B., Gros, C. A versatile class of prototype dynamical systems for complex bifurcation cascades of limit cycles. Sci Rep 5, 12316 (2015). https://doi.org/10.1038/srep12316
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep12316
This article is cited by
-
How to test for partially predictable chaos
Scientific Reports (2017)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.