Abstract
Transition metal diborides are ceramic materials with potential applications as hard protective thin films and electrical contact materials. We investigate the possibility to obtain age hardening through isostructural clustering, including spinodal decomposition, or ordering-induced precipitation in ternary diboride alloys. By means of first-principles mixing thermodynamics calculations, 45 ternary M11–xM2xB2 alloys comprising MiB2 (Mi = Mg, Al, Sc, Y, Ti, Zr, Hf, V, Nb, Ta) with AlB2 type structure are studied. In particular Al1–xTixB2 is found to be of interest for coherent isostructural decomposition with a strong driving force for phase separation, while having almost concentration independent a and c lattice parameters. The results are explained by revealing the nature of the electronic structure in these alloys and in particular, the origin of the pseudogap at EF in TiB2, ZrB2 and HfB2.
Similar content being viewed by others
Introduction
Metal diborides constitute a large subgroup of the boride family crystalizing in several different structures. In particular those with the AlB2 type crystal structure are studied intesively for a wide range of properties: MgB2 demonstrates high-temperature superconductivity1,2, AlB2 is used for controlling solidification in Al metal casting3 and transition metal diborides, such as TiB2, ZrB2 and HfB2, combines high hardness, chemical and thermal stability with high electrical conductivity4,5,6,7,8. Also boron-richer metal borides, like the XYB14 phases9,10 as well as transition metal monoborides11,12 have demonstrated impressive mechanical properties in experimental and computational studies. These properties make the borides interesting candidates in the form of thin films for hard protective coatings for, e.g., cutting tools and for electrical contacts in demanding environments. However, their applications in industry have been hampered due to the technological challenge to synthesize boride thin films using physical vapor deposition13,14,15.
Despite the complexity involved, synthesis of thin films from diboride compound targets, such as TiB2, is at present industrially utilized through magnetron sputtering, with resulting hard or superhard TiB2+x, depending on degree of overstoichiometry6,16. Growth of superhard NbB2−x thin films17, the possibility for epitaxial growth of ZrB2 as conductive contact layers on, e.g., SiC18 and the role of growth rate, residual gasses and target purity for the film quality19 in magnetron sputtering of diborides has been discussed in the literature. Also, high power impulse magnetron sputtering of ZrB220 has been performed and even arc-evaporation of TiB2 targets for the growth of boron-containing thin films have been demonstrated13,21.
As the field of thin film diborides for coatings applications is opening up, alloying is a natural next step for property enhancement. For Ti1–xAlxN hard coatings, isostructural clustering has been demonstrated as one of the reasons behind their technological success22,23, in a ceramics analogy of the age hardening of, e.g., AlCu alloys24. This raises the question if similar beneficial age-hardening phenomena are possible during heat treatment of diboride alloy films. Furthermore, only few studies have investigated the electronic structure of ternary diborides25 and there are outstanding questions also for binary diborides appreciating considerable theoretical investigations26,27,28.
Thus, a computational investigation which allows for an efficient and accurate derivation of alloy energetics29,30 and electronic structure is motivated to guide the emerging experimental efforts in this field. In this work we start by a first-principles scan of the mixing thermodynamics of all the 45 alloy systems formed by all  B2 combinations of the ten binary diborides MgB2, AlB2, ScB2, YB2, TiB2, ZrB2, HfB2, VB2, NbB2 and TaB2, all reported to crystalize in the AlB2 type structure. Several alloys and in particular Al1–xTixB2, are identified as potential candidates for age-hardening due to isostructural decomposition tendency with limited lattice mismatch and are analyzed more in detail. Finally, the observed trends are explained by studies of the electronic structure of the alloys and how they change with composition. The findings are discussed in light of a here revealed modified explanation for the exisistance of a pseudogap at the Fermi level of TiB2: d-d electron interactions between transition metals in the simple hexagonal geometry.
B2 combinations of the ten binary diborides MgB2, AlB2, ScB2, YB2, TiB2, ZrB2, HfB2, VB2, NbB2 and TaB2, all reported to crystalize in the AlB2 type structure. Several alloys and in particular Al1–xTixB2, are identified as potential candidates for age-hardening due to isostructural decomposition tendency with limited lattice mismatch and are analyzed more in detail. Finally, the observed trends are explained by studies of the electronic structure of the alloys and how they change with composition. The findings are discussed in light of a here revealed modified explanation for the exisistance of a pseudogap at the Fermi level of TiB2: d-d electron interactions between transition metals in the simple hexagonal geometry.
Results and Discussion
As an illustrative example of a temperature where hard coatings are used, the mixing trends at 1000 °C are derived for all considered 45 ternary systems. The mixing trend for the composition 
 B2 is shown for each alloy in the upper right part of the matrix in Fig. 1.
B2 is shown for each alloy in the upper right part of the matrix in Fig. 1.
Upper-right: Overview of calculated mixing tendency in 
 B2 systems at T = 1000 °C. “C” is clustering, “O” is ordering, “Mix(c)” is solid solution forming with clustering tendency at 0 K, “Mix(o)” is solid solution forming with ordered compounds stable at 0 K. Lower-left: Volume misfit δV of the pairs of binaries and the bulk modulus for the
B2 systems at T = 1000 °C. “C” is clustering, “O” is ordering, “Mix(c)” is solid solution forming with clustering tendency at 0 K, “Mix(o)” is solid solution forming with ordered compounds stable at 0 K. Lower-left: Volume misfit δV of the pairs of binaries and the bulk modulus for the 

 ternary. Red and blue colors follow the ordering or clustering cases above for clarity.
ternary. Red and blue colors follow the ordering or clustering cases above for clarity.
Clustering, the formation of separate M1-rich and M2-rich regions, is found to be favored at 1000 °C in 16 cases marked with blue colored “C” in the upper right part of the matrix. Ordered 
 B2 phases are predicted to be lowest in free energy at 1000 °C for the seven cases marked with red colored “O”. Remaining 22 alloy systems are predicted to demonstrate solid solution miscibility at 1000 °C with either clustering or ordering tendencies at 0 K.
B2 phases are predicted to be lowest in free energy at 1000 °C for the seven cases marked with red colored “O”. Remaining 22 alloy systems are predicted to demonstrate solid solution miscibility at 1000 °C with either clustering or ordering tendencies at 0 K.
One common reason for lack of miscibility in isostructural alloys, according to the Hume-Rhothery rules, is lattice misfit. In the AlB2 type structure both a- and c-parameters should be considered, but as a first measure on lattice mismatch we study the volume misfit

of the alloys. These values are presented in the lower left part of the Fig. 1 matrix. Also shown is the bulk modulus for the mixed 
 B2 compositions. It can be seen that all systems with a good solid solution formation ability has a limited volume mismatch of
B2 compositions. It can be seen that all systems with a good solid solution formation ability has a limited volume mismatch of  . All alloys with larger mismatch favor either ordering or clustering.
. All alloys with larger mismatch favor either ordering or clustering.
However, also lattice-matched systems can display clustering. Such alloys, with a small lattice mismatch, but a strong driving force for clustering are of particular interest for age-hardening potential. They are likely to form fully coherent interfaces and display spinodal decomposition with large composition fluctuations even when diffusion is limited, a concern for phase transitions in diborides31. The resulting nanostructure in the lattice can decrease dislocation mobility and increase hardness. For this reason, the alloys Al1–xTixB2, Al1–xVxB2 and Mg1–xHfxB2 deserves further attention as they are predicted to display clustering and a small volume misfit as can be seen in the Fig. 1 matrix. Fig. 2(a) shows ΔH of ordered and disordered alloys for these system, as well as for the ordering Sc1–xVxB2 system for comparison, calculated with the 192-atoms SQS supercells for the disordered phases. Panel b) shows the a- and c-parameters as a function of composition for these systems.
Al1–xTixB2 is an almost perfectly lattice matched system, as can be seen in Fig. 2(b), but nevertheless displays a strong driving force for phase separation in terms of a positive mixing enthalpy and mixing free energy at 1000 °C, in particular in the AlB2-rich compositions. This is a very similar situation to the well studied Ti1–xAlxN alloys, where electronic structure effects have been found to be the origin of spinodal decomposition.32,33 The mixing enthalpies calculated for the disordered Al1–xTixB2 solid solutions have a maximum value of 0.125 eV/f.u. at  . This is much lower than the values obtained by Zhang et al.25 who got 0.195 eV/f.u. using ordered structures, indicating the importance of a careful modeling of configurational disorder in this system. Our mixing enthalpy calculations strengthen the view of Ref 34 that, despite conflicting results, bulk experiments indicate lack of equilibrium miscibility of TiB2 and AlB2 within the temperature stability range of pure AlB2, T < 980 °C.
. This is much lower than the values obtained by Zhang et al.25 who got 0.195 eV/f.u. using ordered structures, indicating the importance of a careful modeling of configurational disorder in this system. Our mixing enthalpy calculations strengthen the view of Ref 34 that, despite conflicting results, bulk experiments indicate lack of equilibrium miscibility of TiB2 and AlB2 within the temperature stability range of pure AlB2, T < 980 °C.
For Al1–xVxB2 alloys, the clustering driving force is weaker and the system is on the verge of mixing, while Mg1–xHfxB2 is predicted to have a distinct clustering tendency for intermediate compositions, at 1000 °C. The Sc1–xVxB2 alloys on the other hand illustrate the mixing energetics of a system where a layered ScVB4 ordered structure is predicted to be stable even when configurational entropy of the disordered alloys are considered at 1000 °C, possibly demonstrating precipitation of ScVB4 in  compositions.
compositions.
The bonding physics behind the configurational tendencies of the alloys can be sought in their electronic density of states (DOS). The DOS of the illustrative case TiB2 is shown in Fig. 3(a). It displays the characteristic psuedogap at the Fermi level that has been debated in the literature and suggested to be due to the combination of B-B bonds, a charge transfer from the metal to the boron layer and a strong bonding between B and Ti, seen in their common DOS peak around 3 eV below EF.26,27 However, less discussed35, one can also see that the DOS closest below and above EF is dominated by Ti states with only a minimal inmixture of B character. Fig. 3(b) shows the symmetry projections of Ti 3d states demonstrating that the region between 2.5 and 0 eV below EF is dominated by the orbitals of eg symmetry, which extend in real space in the metal plane and orthogonal out of it in the direction of the metal atoms in the next metal plane above and below. On the other hand, the sharp peak at −3 eV is dominated by the t2g orbital in the xz-direction, which in our unit cell set-up correspond to the direction of four of the nearest B neighbors.
To investigate if the pseudo gap could have an origin in the bonding of metal d-states as much as the metal-boron bondings, Fig. 3(c) shows pure Ti in the simple hexagonal structure resulting when removing B2 from the AlB2 structure unit cell. Also shown is the DOS of B2 when Ti is removed as well as C2 in the same geometry modeling the effect of two electrons transferred from each metal atom to the two boron atoms. Interestingly, it can be seen that a distinct pseudo gap at EF appears also in the case of simple hexagonal Ti without boron. Almost precisely two out of four Ti valence electrons occupy the d-orbitals in this case, while the remaining valence electrons are of more delocalized character. Also for the C2 model, the EF falls into a pseudo gap. Thus, we suggest that the distinct pseudo gap in transition metal diborides, present close to EF for (Ti,Zr,Hf)B2, has its origin in a split of the d-orbitals caused by d–d interaction in the simple hexagonal geometry. This effect is then enhanced by charge transfer of electrons from the metal to boron as well as metal-boron bonding in the diborides.
Figure 3(d,e) show the effect of Al mixing into TiB2. While the B DOS is largely unchanged, the Ti partial DOS is changing. In particular, the peak corresponding to the 3d–eg states just below EF shifts towards higher energies as compared to pure TiB2. In Al0.875Ti0.125B2, this peak in the Ti partial DOS is right at EF. This can be understood as the d–d bonding, responsible for the pseudo gap formation in the Ti d-band, is disrupted by the introduction of Al, which d-orbitals are too high above the valence states in energy to take any part in the bonding.
One can also see that the sharp Ti peak 3 eV below EF corresponding to Ti-B bonds is smeared out, possibly weakened, upon Al addition. These disturbances and breaking of d–d bonding in the electronic structure is the likely explanation for the large positive mixing enthalpy of Al1–xTixB2 and the driving force for clustering.
Finally, Fig. 3(e) shows that VB2 and ScB2 demonstrate more or less rigid band shifts as compared to TiB2. The Sc0.5V0.5B2 alloys, as expected, retain EF in the pseudo gap, in a direct parallel to the composition which is energetically favored, seen in the corresponding panel of Fig. 2(a). Thus, alloying with higher or lower valency transition metals might be considered to increase the DOS at EF of TiB2 and ZrB2 and thus the number of carriers in electrical contact applications. However, such attempts need to be balanced against disorder-induced scattering.
In conclusion, the mixing trends in 45 ternary diboride alloys of the AlB2 structure have been revealed. Metastable Al1–xTixB2 alloys are found to have a strong thermodynamic driving force for isostructural clustering combined with a small lattice mismatch and a high bulk modulus, which qualifies them for age hardening potential in thin film applications. The mixing trends can be understood from an analysis of the electronic structure and volume misfit revealed for the ternary diboride alloys. Metal d–d bonding is found to be part of the explanation for the pseudogap in the DOS of transition metal diborides.
Methods
We use the density functional theory and the projector augmented-wave method36 as implemented in the Vienna Ab-Initio Simulation package (VASP)37,38 and the generalized gradient approximation as suggested by Perdew, Burke and Ernzherhof for exchange-correlation energies39. For each considered structure the total energy of the calculation is converged to within 1 meV/atom with respect to the k-point sampling of the Brillouin zone. A plane-wave energy cut-off of 400 eV is used. Random 
 B2 alloys are modeled with the special quasi-random structure (SQS) method40 including 72 atoms per cell and the compositions x = 0.25, 0.50 and 0.75, in the initial scan and large 192 atom supercells with the compositions x = 0.125, 0.25, 0.375, 0.50, 0.625, 0.75 and 0.875 in the subsequent refined calculuations. Convergency tests show that the smaller cells give qualitative accurate representation of the mixing trends and converged equilibrium volumes, while the larger supercells are needed to obtain quantitative convergency of the mixing enthalpies.
B2 alloys are modeled with the special quasi-random structure (SQS) method40 including 72 atoms per cell and the compositions x = 0.25, 0.50 and 0.75, in the initial scan and large 192 atom supercells with the compositions x = 0.125, 0.25, 0.375, 0.50, 0.625, 0.75 and 0.875 in the subsequent refined calculuations. Convergency tests show that the smaller cells give qualitative accurate representation of the mixing trends and converged equilibrium volumes, while the larger supercells are needed to obtain quantitative convergency of the mixing enthalpies.
The mixing enthalpies as a function of composition x,  , at zero pressure is calculated as
, at zero pressure is calculated as

and for the configurationally disordered alloys the mixing free energy is approximated as  where
where  per formula unit (f.u.) is the configurational entropy of an ideal solution on the metal sublattice. Both sublattices are assumed to be stoichiometric.
per formula unit (f.u.) is the configurational entropy of an ideal solution on the metal sublattice. Both sublattices are assumed to be stoichiometric.
In addition 10 ordered alloy structure with 24 atoms per cell at the compositions x = 0.25, 0.50 and 0.75 were considered for all systems. These were generated maximizing the numbers of M1-M2 bonds on the first two metal-sublattice coordination shells. The consideration of the pure binaries, the disordered SQS structures and the sample of ordered structures makes it possible to accurately scan the mixing trends in these ternary systems.
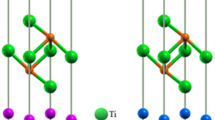
Figure 4 illustrates, using the Jmol package41, (a): the hexagonal AlB2 crystal structure, (b): a 192 atoms Al0.5Ti0.5B2 SQS supercell and (c): the layered ordered configuration found to be the lowest energy structure for, among other systems, ScVB4. Boron atoms are shown in green, while metal atoms are shown in grey (Ti), black (Al), white (V) and dark red (Sc).
Additional Information
How to cite this article: Alling, B. et al. A theoretical investigation of mixing thermodynamics, age-hardening potential and electronic structure of ternary M11-xM2xB2 alloys with AlB2 type structure. Sci. Rep. 5, 9888; doi: 10.1038/srep09888 (2015).
References
Nagamatsu, J., Nakagawa, N., Muranaka, T., Zenitani, Y. & Akimutsu, J. Superconductivity at 39 K in magnesium diboride. Nature 410, 63 (2001).
Buzea, C. & Yamashita, T. Review of the superconducting properties of MgB2 . Supercond. Sci. Tech. 14, R115 (2001).
Wang, X. M. The formation of AlB2 in an Al-B master alloy. J. Alloy. Compd. 403, 283 (2005).
Fahrenholtz, W. G., Hilmas, G. E., Talmy, I. G. & Zaykoski, J. A. Refractory Diborides of Zriconium and Hafnium. J. Am. Ceram. Soc. 90, 1347 (2007).
Passarone, A., Valenza, F. & Muolo, M. L. A review of transition metal diborides: from wettability studies to joining. J. Mater. Sci. 47, 8275 (2012).
Berger, M., Karlsson, L., Larsson, M. & Hogmark, S. Low stress TiB2 coatings with improved tribological properties. Thin Solid Films 401, 179 (2001).
Kalfagiannis, N., Volonakis, G., Tsetseris, L. & Logothetidis, S. Excess of boron in TiB2 superhard thin films: a combined experimental and ab initio study. J. Phys. D Appl. Phys. 44, 385402 (2011).
Fahrenholtz, W. G. & Hilmas, G. E. Oxidation of ultra-high temperature transition metal diboride ceramics. Int. Mater. Rev. 57, 61 (2012).
Kölpin, H., Music, D., Henkelman, G. & Schneider, J. M. Phase stability and elastic properties of XMgB14 studied by ab initio calculations (X=Al, Ge, Si, C, Mg, Sc, Ti, V, Zr, Nb, Ta, Hf. Phys. Rev. B 78, 054122 (2008).
Emmerlich, J., Thieme, N., to Baben, M., Music, D. & Schneider, J. M. Stability, elastic properties and fracture toughness of A10.75 X 0.75B14(X=Sc, Ti, V, Cr, Y, Zr, Nb, Mo) investigated using ab initio calculations. J. Phys.-Condens. Mat. 25, 335501 (2013).
Madtha, S., Lee, C. & Chandran, K. S. R. Physical and mechanical properties of nanostructured titanium boride (TiB) ceramic. J. Am. Ceram. Soc. 91, 1319 (2008).
Trinkle, D. R. Lattice and elastic constants of titanium-niobium monoborides containing aluminum and vanadium. Scripta. Mater. 56, 273 (2007).
Knotek, O., Löffler, F., Böhmer, M., Breidenbach, R. & Stössel, C. Ceramic cathodes for arc-physical vapour deposition: development and application. Surf. Coat. Tech. 49, 263 (1991).
Mitterer, C. Borides in thin film technology. J. Solid State Chem. 133, 279 (1997).
Rebholz, C., Leyland, A., Schneider, J. M., Voevodin, A. A. & Matthews, A. Structure, hardness and mechanical properties of magnetron-sputtered titanium-aluminium boride films. Surf. Coat. Tech. 120-121, 412 (1999).
Mayrhofer, P. H., Mitterer, C., Wen, J. G., Greene, J. E. & Petrov, I. Self-organized nanocolumnar structure in superhard TiB2 thin films. Appl. Phys. Lett. 86, 131909 (2005).
Nedfors, N. et al. Superhard NbB2−x thin films deposited by dc magnetron sputtering. Surf. Coat. Tech. 257, 295 (2014).
Tengdelius, L. et al. Magnetron sputtering of epitaxial ZrB2 thin films on 4H-SiC(0001) and Si(111). Phys. Status Solidi. A 211, 636 (2014).
Tengdelius, L. et al. Direct current magnetron sputtered ZrB2 thin films on 4H-SiC(0001) and Si(100). Thin Solid Films 555, 285 (2014).
Samuelsson, M., Jensen, J., Helmersson, U., Hultman, L. & Högberg, H. ZrB2 thin films grown by high power impulse magnetron sputtering from a compound target. Thin Solid Films. 526, 163 (2012).
Fager, H., Andersson, J. M., Jensen, J., Lu, J. & Hultman, L. Thermal stability and mechanical properties of amorphous coatings in the Ti-B-Si-Al-N system grown by cathodic arc evaporation from TiB2, Ti33Al67 and Ti85Si15 cathodes. J. Vac. Sci. Technol. A 32, 061508 (2014).
Mayrhofer, P. H. et al. Self-organized nanostructures in the Ti-Al-N system. Appl. Phys. Lett. 83, 2049 (2003).
Alling, B., Karimi, A., Hultman, L. & Abrikosov, I. A. First-principles study of the effect of nitrogen vacancies on the decomposition pattern in cubic Ti1–xAlxN1–y . Appl. Phys. Lett. 92, 071903 (2008).
Ringer, S. & Hono, K. Microstructural evolution and age hardening in aluminium alloys: Atom probe field-ion microscopy and transmission electron microscopy studies. Mater. Charact. 44, 101 (2000).
Zhang, H. L., Han, Y. F., Wang, J., Dai, Y. B. & Sun, B. D. An ab initio molecular dynaimcs study on the structural and electronic properties of AlB2, TiB2 and (Alx,Ti(1–x)B2 in Al-Ti-B master alloys. J. Alloy. Compd. 585, 529 (2014).
Vajeeston, P., Ravindran, P., Ravi, C. & Asokamani, R. Electronic structure, bonding and ground-state properties of AlB2-type transition-metal diborides. Phys. Rev. B 63, 045115 (2001).
Ivanovskii, A. L. Mechanical and electronic properties of diborides of transition 3d–5d metals from first principles: Toward search of novel ultra-incompressible and superhard materials. Prog. Mater. Sci. 57, 184 (2012).
Wagner, F. R., Baranov, A. I. & Kohout, Y. G. M. A Position-Space View on Chemical Bonding in Metal Diborides with AlB2 Type of Crystal Structure. Z. Anorg. Allg. Chem. 639, 2025 (2013).
Lind, H., Tasnádi, F. & Abrikosov, I. A. Systematic theoretical search for alloys with increased thermal stability for advanced hard coatings applications. New J. Phys. 15, 095010 (2013).
Kerdsongpanya, S., Alling, B. & Eklund, P. Phase stability of ScN-based solid solutions for thermoelectric applications from first-principles calculations. J. Appl. Phys. 114, 073512 (2013).
Schmidt, H., Borchardt, G., Weber, S. & Scherrer, H. Diffusion in Transition Metal Diborides - An Overview. Defect. Diffus. Forum 263, 219 (2007).
Alling, B. et al. Mixing and decomposition thermodynamics of c-Ti1–xAlxN from first-principles calculations. Phys. Rev. B 75, 045123 (2007).
Alling, B., Karimi, A. & Abrikosov, I. A. Electronic origin of the isostructural decomposition in cubic M1–xAlxN (M=Ti, Cr, Sc, Hf): A first-principles study. Surf. Coat. Tech. 203, 883–886 (2008).
Materials Science International Team MSIT, Anatoliy Bondar. Al-B-Ti (Aluminium - Boron - Titanium), vol. 11A1: Light Metal Systems Materials Science International Services GmbH: Stuttgart, Germany, 2004).
Xu, X. et al. The thermodynamic, electronic and elastic properties of the early-transition-metal diborides with AlB2-type structure: A density functional theory study. J. Alloy Compd. 607, 198 (2014).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953 (1994).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169 (1996).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758 (1999).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865 (1996).
Zunger, A., Wei, S. H., Ferreira, L. G. & Bernard, J. E. Special quasirandom structures. Phys. Rev. Lett. 65, 353 (1990).
Hanson, B., Jmol: an open-source Java viewer for chemical structures in 3D. http://www.jmol.org/. (2012) Date of access:13/02/2015
Acknowledgements
Financial support from the Swedish Research Council (VR) is acknowledged by B.A., Grant No. 621-2011-4417 and R.A., grant No. 621-2011-4249. H.H. acknowledges the Swedish Government Strategic Research Area in Materials Science on Functional Materials at Linköping University (Faculty Grant SFO-Mat-LiU No. 2009-00971) for financial support. L.H. acknowledges the Knut and Alice Wallenberg Foundation for a Wallenberg Scholar Grant. JR acknowledges funding from ERC under Grant agreement no [258509]. The simulations were carried out using supercomputer resources provided by the Swedish National Infrastructure for Computing (SNIC) carried out at the National Supercomputer Centre (NSC) and the Center for high performance computing (PDC).
Author information
Authors and Affiliations
Contributions
B.A. initiated the project. B.A. carried out the calculations. B.A., H.H., R.A., J.R. and L.H. contributed in the discussion and interpretation of the results. B.A. wrote the manuscript with input from H.H., R.A., J.R. and L.H.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Alling, B., Högberg, H., Armiento, R. et al. A theoretical investigation of mixing thermodynamics, age-hardening potential and electronic structure of ternary M11–xM2xB2 alloys with AlB2 type structure. Sci Rep 5, 9888 (2015). https://doi.org/10.1038/srep09888
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep09888
This article is cited by
-
Ceramic transition metal diboride superlattices with improved ductility and fracture toughness screened by ab initio calculations
Scientific Reports (2023)
-
First-principles demonstration of band filling-induced significant improvement in thermodynamic stability and mechanical properties of Sc\(_{1-x}\)Ta\(_{x}\)B\(_{2}\) solid solutions
Scientific Reports (2023)
-
Ab initio inspired design of ternary boride thin films
Scientific Reports (2018)
-
New design for highly durable infrared-reflective coatings
Light: Science & Applications (2017)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.